Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 378
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ность для всех частот и температур равна единице (т.е. все падающее излучение поглощается), называются абсолютно черными телами (АЧТ). Г. Кирхгоф показал, что наиболее близка к АЧТ сферическая полость с малым входным отверстием. Излучение, попавшее через отверстие внутрь полости, не сможет из-за многократных отражений от стенок выйти наружу, так что подобная полость выглядит как АЧТ (поглощает все излучение, которое проходит через отверстие). Если поддерживать постоянную температуру стенок полости T, то в результате процессов испускания и поглощения электромагнитного излучения нагретыми стенками устанавливается динамическое равновесие: количество излучения определенной частоты, испускаемого стенкой, равно количеству излучения, поглощаемого стенкой.
Закон Кирхгофа: отношение испускательной и поглощательной способностей тела не зависит от природы тела и является универсальной для всех тел функцией частоты излучения и температуры тела:
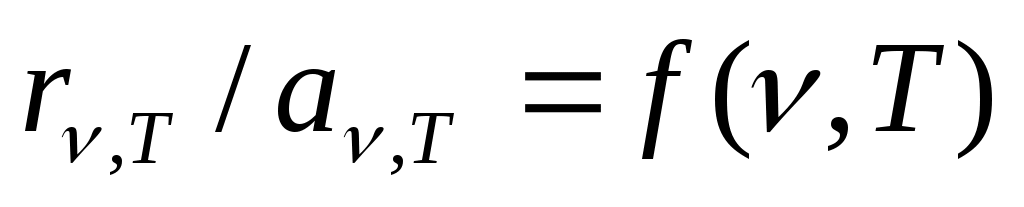 .
.
У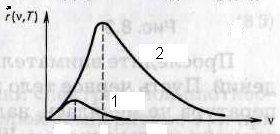 ниверсальная функция Кирхгофа и есть испускательная способность АЧТ (
ниверсальная функция Кирхгофа и есть испускательная способность АЧТ (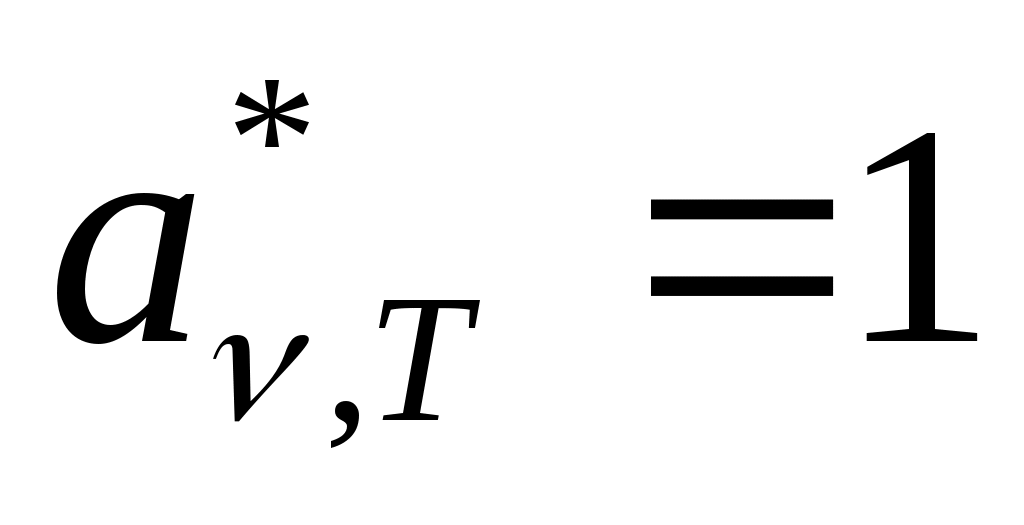 ) :
) : 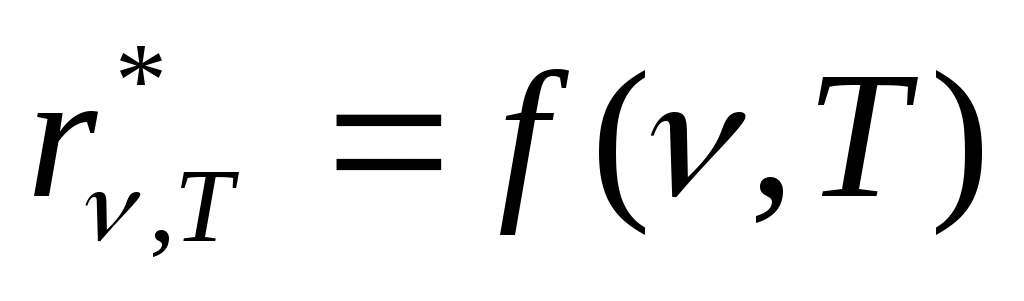 . Если излучение нагретого АЧТ (излучение, выходящее из отверстия в полости) с помощью спектрального прибора разложить в спектр и измерить энергию, падающую на единицу площади экрана в единицу времени как функцию частоты и температуры тела, то эта зависимость
. Если излучение нагретого АЧТ (излучение, выходящее из отверстия в полости) с помощью спектрального прибора разложить в спектр и измерить энергию, падающую на единицу площади экрана в единицу времени как функцию частоты и температуры тела, то эта зависимость 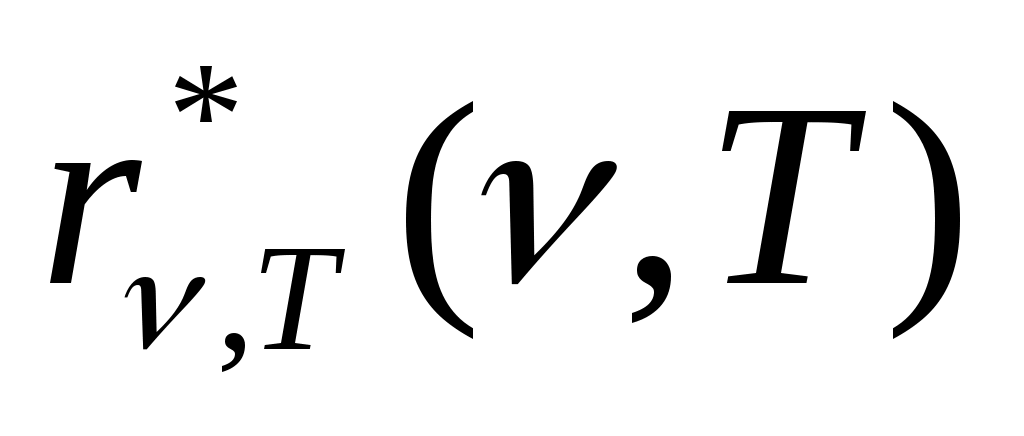 имеет вид (рис.) (кривая 2 соответствует более высокой температуре полости, чем кривая 1). С учетом того, что площадь под зависимостью
имеет вид (рис.) (кривая 2 соответствует более высокой температуре полости, чем кривая 1). С учетом того, что площадь под зависимостью 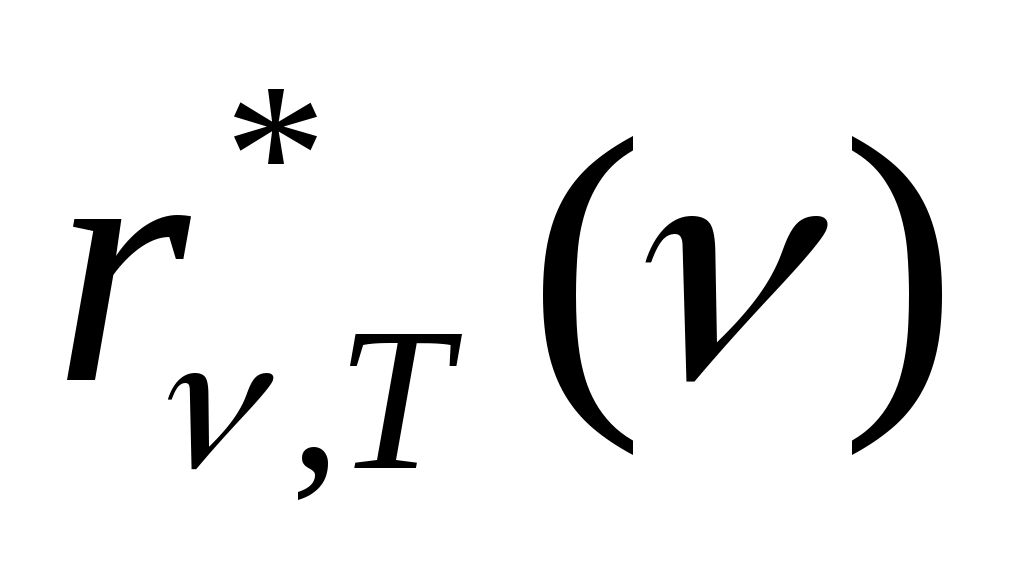 представляет собой энергетическую светимость тела при данной температуре были получены экспериментальные законы излучения АЧТ.
представляет собой энергетическую светимость тела при данной температуре были получены экспериментальные законы излучения АЧТ.
Закон Стефана—Больцмана: энергетическая светимость АЧТ пропорциональна четвертой степени абсолютной температуры,
т.е.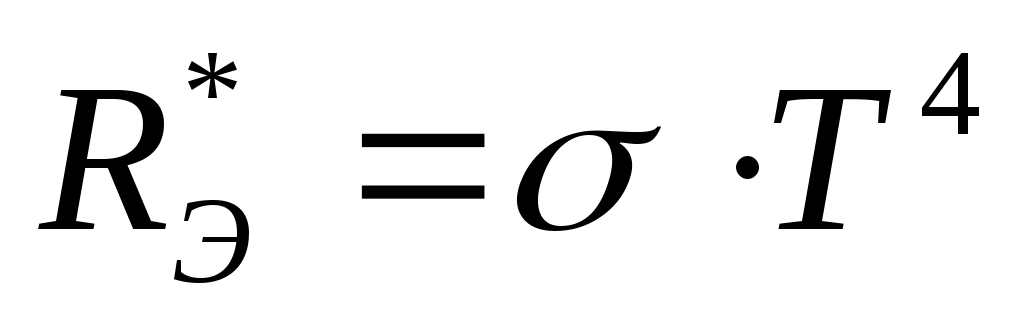 ,где σ = 5,67·10 -8 Вт/(м2·Т4) – постоянная Стефана–Больцмана.
,где σ = 5,67·10 -8 Вт/(м2·Т4) – постоянная Стефана–Больцмана.
Закон смещения Вина: частота νm, на которую приходится максимум испускательной способности АЧТ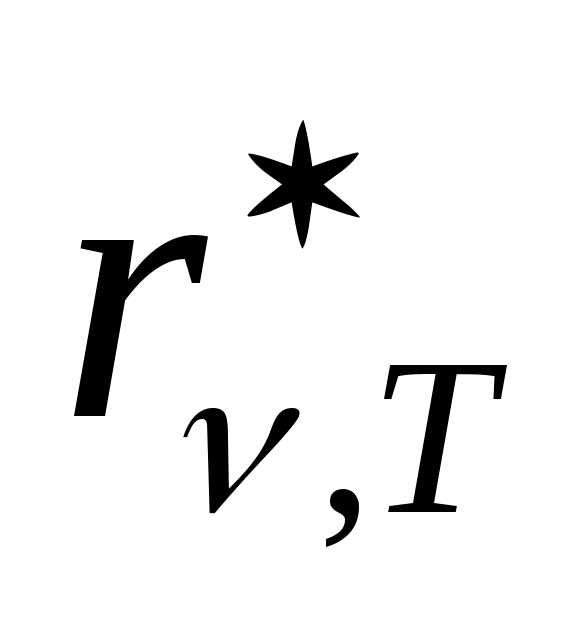 , пропорциональна его температуре: νт=a·Т. a=1,0352·1011 1/(c·K) – постоянная Вина. (Закон Вина записывают также через длину волны: λm= b/T , где b= с/a=2,898·10-3 м·К – тоже называется постоянной Вина).
, пропорциональна его температуре: νт=a·Т. a=1,0352·1011 1/(c·K) – постоянная Вина. (Закон Вина записывают также через длину волны: λm= b/T , где b= с/a=2,898·10-3 м·К – тоже называется постоянной Вина).
Ход экспериментальных кривых для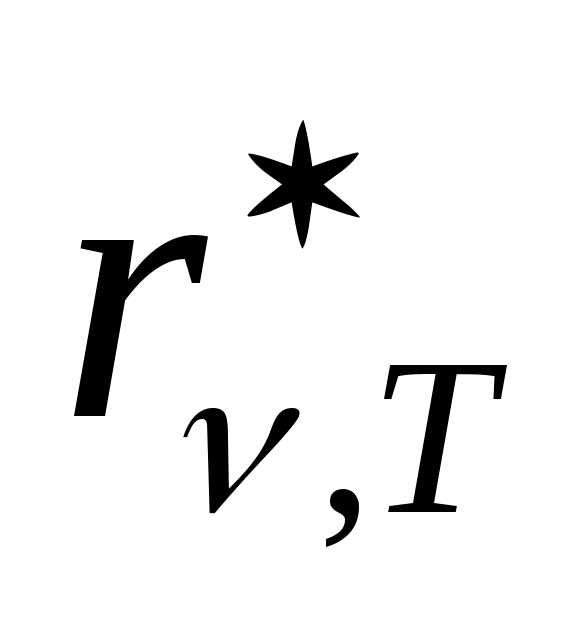 теоретически объяснил М. Планк, предположив, что излучение нагретых тел происходит не непрерывно, а порциями – квантами с энергией hvкаждый, где h=6,6262·10-34 Дж·с – постоянная Планка..
теоретически объяснил М. Планк, предположив, что излучение нагретых тел происходит не непрерывно, а порциями – квантами с энергией hvкаждый, где h=6,6262·10-34 Дж·с – постоянная Планка..
п(
x).Квадрат амплитуды световой волны в какой-либо точке пространства пропорционален числу фотонов, попадающих в эту точку.Иными словами, квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотонов в эту точку.Таким образом, волновые и квантовые свойства света не исключают, а, наоборот, взаимно дополняют друг друга. Квантовые свойства света обусловлены тем, что энергия, импульс и масса излучения сосредоточены в частицах – фотонах. Вероятность нахождения фотонов в различных точках пространства определяется волновыми свойствами света – амплитудой световой волны (квадратом ее модуля).
Далее было установлено, что волновые свойства присущи не только совокупности большого числа одновременно летящих фотонов. Каждый отдельный фотон обладает волновыми свойствами.Волновые свойства фотона проявляются в том, что для него нельзя точно указать, в какую именноточку экрана он попадет после прохождения щели. Можно говорить лишь о вероятности попадания каждого фотонав ту или иную точку экрана.
Такое истолкование связи между волновыми и квантовыми свойствами света сыграло выдающуюся роль в развитии современной физики.
Волновые свойства микрочастиц. Корпускулярно-волновой дуализм присущ не только свету, но и частицам вещества. Эту идею высказал, исходя из соображений симметрии, Луи де Бройль: если свет, который рассматривался как электромагнитная волна, может проявлять корпускулярные свойства, то и частицы вещества должны проявлять волновые свойства.
Согласно этой идее, импульс частицы с массой mи скоростью υ
равен р = mυ, а с другой стороны, он равен p=h/λ. Следовательно, движущейся частице можно поставить в соответствие волну с длиной: λБ=h/p= h/mυ.
Величину λБ называют дебройлевской длиной волны частицы. Экспериментально волновые свойства микрочастиц были обнаружены в опытах по дифракции электронов на кристаллах.
Наличие волновых свойств у частиц вносит ограничения в применимости к ним классической механики, согласно которой частица в любой момент времени занимает определенное положение в пространстве и обладает определенным импульсом.
Когда проводится какое-либо измерение, его результат содержит некоторую неопределенность, обусловленную двумя факторами: корпускулярно-волновым дуализмом и неизбежным взаимодействием наблюдаемого объекта с регистрирующим прибором, приводящим к изменению состояния объекта. Поэтому существует предел, ограничивающий точность измерений. Этот предел не зависит от степени совершенства измерительного прибора, а присущ самой природе вещей. Это и есть принцип неопределенностей Гейзенберга.
Количественные соотношения, выражающие этот принцип для конкретных динамических переменных, называются соотношениями неопределенностей. Наиболее важными являются два из них:
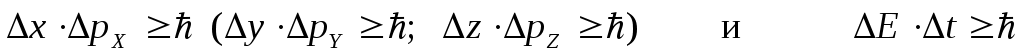 .
.
Первое соотношение утверждает, что нельзя измерить одновременно с абсолютной точностью положение (координату) и проекцию импульса микрочастицы на ту же ось. Чем точнее мы пытаемся определить положение объекта, т.е. чем меньше Δх, тем больше будет неопределенность импульса Δрx . Этот вывод можно понять из следующих рассуждений: пусть мы хотим как можно точнее узнать положение микрочастицы (Δх→0 ). Для этого мы должны использовать фотоны с малой длиной волны λ (именно λ определяет точность измерения положения
Закон Кирхгофа: отношение испускательной и поглощательной способностей тела не зависит от природы тела и является универсальной для всех тел функцией частоты излучения и температуры тела:
У
 ниверсальная функция Кирхгофа и есть испускательная способность АЧТ (
ниверсальная функция Кирхгофа и есть испускательная способность АЧТ (Закон Стефана—Больцмана: энергетическая светимость АЧТ пропорциональна четвертой степени абсолютной температуры,
т.е.
Закон смещения Вина: частота νm, на которую приходится максимум испускательной способности АЧТ
Ход экспериментальных кривых для
Формула Планка для испускательной способности АЧТ:

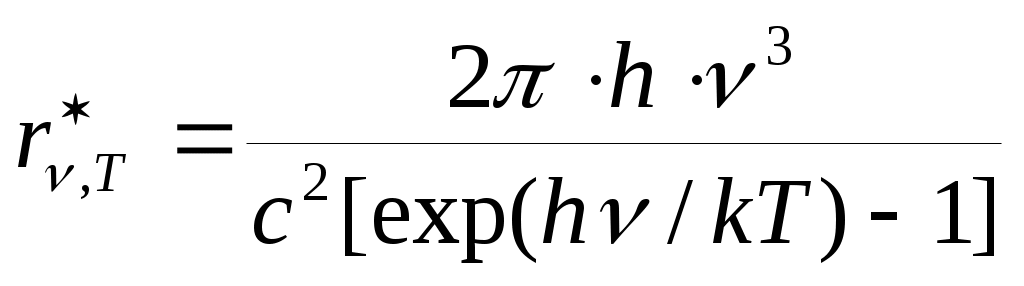
точно согласуется с данными опытов и объясняет все экспериментальные законы теплового излучения тел.
3.4. ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА. ДАВЛЕНИЕ СВЕТА.
Фотоэффект. Классическая теория, представляющая свет как электромагнитные волны, не смогла объяснить законы фотоэффекта и эффект Комптона.
Явлением внешнего фотоэффекта называется вырывание электронов с поверхности тела под действием света достаточно высокой частоты. Экспериментально были установлены следующие закономерности внешнего фотоэффекта:
-
Максимальная кинетическая энергия фотоэлектронов линейно растет с увеличением частоты света и не зависит от его интенсивности.
-
Для каждого вещества существует т.н. «красная граница» фотоэффекта, т.е., наименьшая частота νМИН, при которой еще возможен фотоэффект.
-
Число фотоэлектронов, вырываемых светом из катода за 1с, прямо пропорционально интенсивности света.
-
Фотоэффект практически безынерционен, фототок возникает практически мгновенно после начала освещения катода при условии, что частота света ν ≥ νМИН .
А.Эйнштейн пришел к выводу, что свет распространяется в пространстве и поглощается веществом в виде фотонов – квантов электромагнитного поля с энергией εf = hv.При взаимодействии с веществом фотон целиком передает свою энергию одному электрону. Эта энергия затрачивается на работу выхода электрона из вещества АВЫХ и сообщение вылетевшему электрону кинетической энергии EКИН:
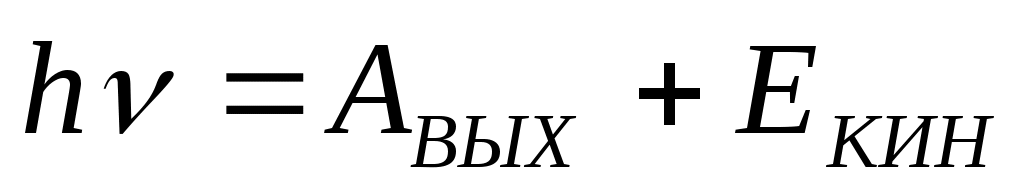 (формула Эйнштейна).
(формула Эйнштейна).
Это выражение объясняет все экспериментальные законы фотоэффекта. В частности, «красную границу» фотоэффекта, т.е., νМИН= АВЫХ/h. Кроме того, фототок прекращается, т.е. электроны не долетают до анода, при приложении между электродами т.н. задерживающей разности потенциалов 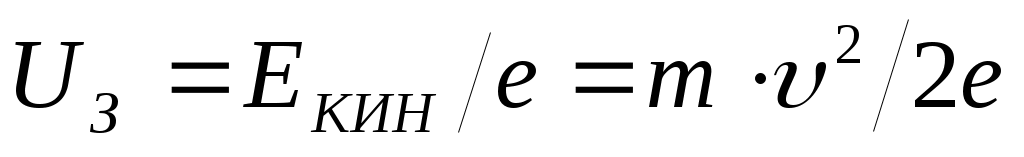 .
.
Эффект Комптона состоит в наблюдении у рассеянного на веществе рентгеновского излучения увеличения длины волны. Он не объясним с волновой точки зрения, т.к. согласно ей при прохождении электромагнитной волны через вещество возникает вторичное излучение с той же самой длиной волны. Этот эффект легко объясняется, если его рассматривать как упругое соударение двух частиц: фотона (f) и неподвижного электрона (e) (рассеяние фотона на электроне) и записать законы сохранения импульса и энергии:
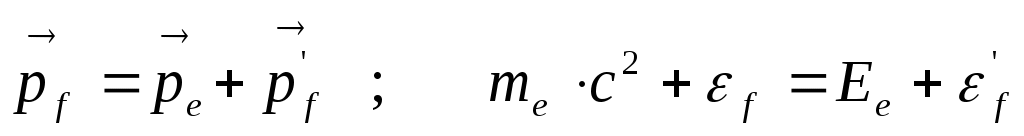 .
.
Учтем, что энергия электрона после столкновения 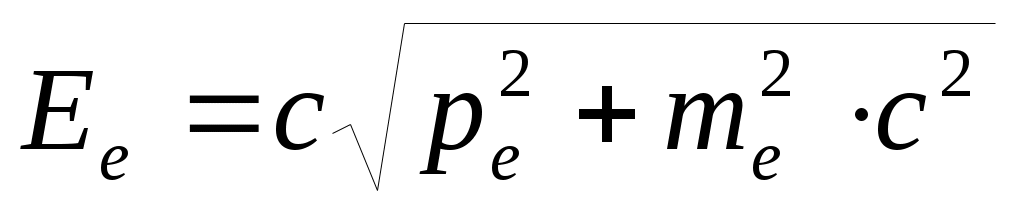 ; εf=hν=hc/λ и εf’=hν’=hc/λ’ – энергии налетающего и рассеянного фотонов, соответственно; θ – угол рассеяния, т.е. угол между векторами импульсов фотонов
; εf=hν=hc/λ и εf’=hν’=hc/λ’ – энергии налетающего и рассеянного фотонов, соответственно; θ – угол рассеяния, т.е. угол между векторами импульсов фотонов 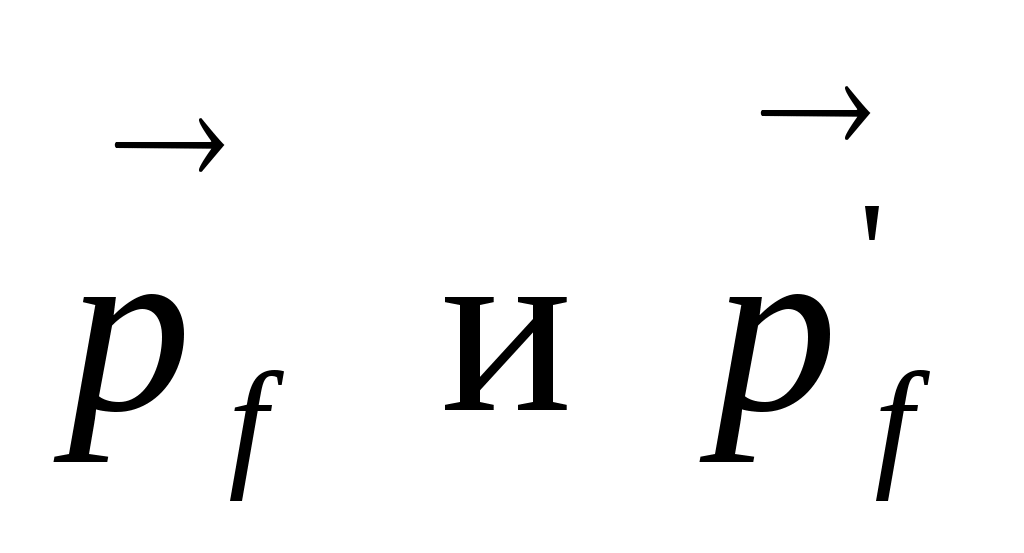 . Так как электромагнитная волна, обладающая энергией Е, имеет импульс р = Е/c(это вытекает из общего выражения СТО для энергии
. Так как электромагнитная волна, обладающая энергией Е, имеет импульс р = Е/c(это вытекает из общего выражения СТО для энергии 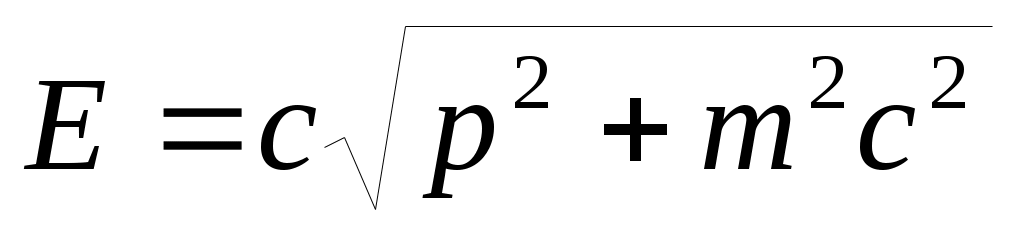 при m= 0), то такое же соотношение должно выполняться и для импульса фотона:pf= εf/c = hv/c=h/λ=ħ·k, где λ и k=2π/λ - длина волны и модуль волнового вектора
при m= 0), то такое же соотношение должно выполняться и для импульса фотона:pf= εf/c = hv/c=h/λ=ħ·k, где λ и k=2π/λ - длина волны и модуль волнового вектора  , соответственно, ħ=h/2π – тоже постоянная Планка.
, соответственно, ħ=h/2π – тоже постоянная Планка.
Решая совместно уравнения получим:
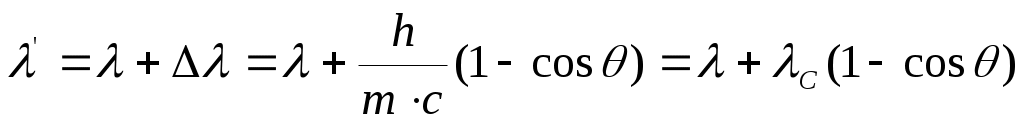 ,
,
где 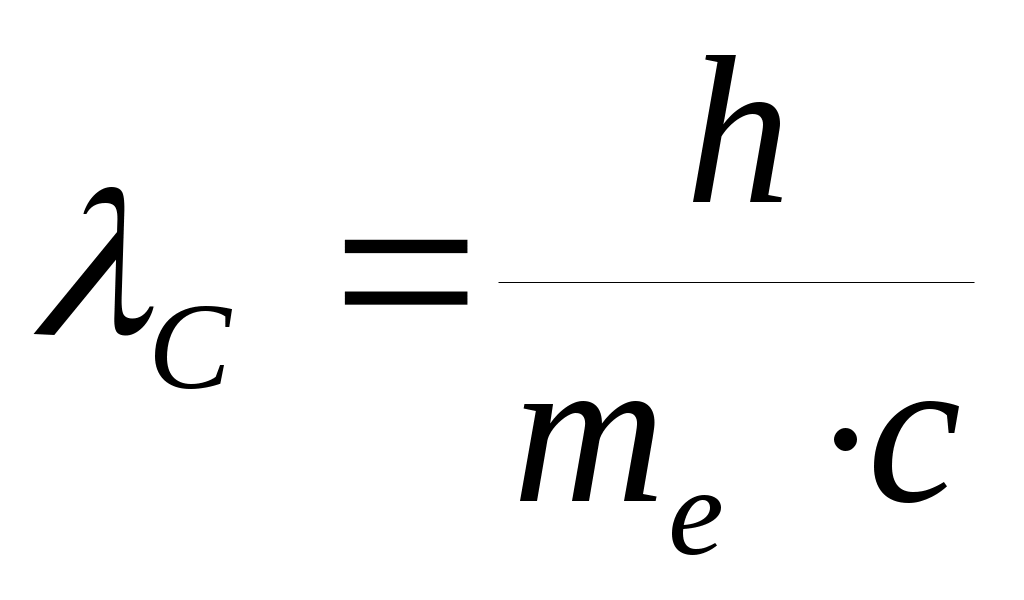 – т.н. комптоновская длина волны для электрона.
– т.н. комптоновская длина волны для электрона.
Рассматривая свет как поток частиц-фотонов удалось также объяснить давление света на поверхность.
Давление света. Фотоны, обладая импульсами, попадая на поверхность, оказывают на нее давление. Если п – плотность фотонов, то на единицу поверхности в единицу времени попадает п·с фотонов. При поглощении каждый фотон сообщает поверхности импульс рf = hv/c, тогда все фотоны сообщат единице площади поверхности в единицу времени импульс (а это и есть давление):
Р =(hv/c)· п·с= εf ·n.
Но величина εf ·nравна энергии фотонов, заключенных в единице объема, т.е., объемной плотности электромагнитной энергии w. Таким образом, Р = wили с учетом того, что часть фотонов отражается: Р = w(1+ ρ), где ρ –коэффициент отражения, равный 1 при полном отражении фотонов, и 0 при их полном поглощении. Полученный результат совпадает с выражением для давления света в электромагнитной теории.
3.5. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ.
Корпускулярно-волновой дуализм света. Т.о., в одних опытах (дифракция, интерференция, поляризация) свет проявляет волновые свойства, в других же (тепловое излучение, фотоэффект, эффект Комптона) он ведет себя как поток частиц-фотонов, но никогда не проявляет волновые и корпускулярные свойства одновременно. Волновая и квантовая теории света дополняют друг друга. Двойственная природа света получила название корпускулярно-волнового дуализма света и находит свое выражение в формулах, определяющих основные характеристики фотонов. Как видно из этих формул, корпускулярные характеристики фотона – энергия εf = hvиимпульс рf = hv/c=h/λ– связаны с волновыми характеристиками света : его частотой ν и длиной волны λ.
Большая группа оптических явлений – интерференция, дифракция, поляризация – полностью объясняется в волновой оптике. Однако, если «перемещаться» от длинных волн в сторону более коротких, то волновые свойства света будут проявляться все слабее, уступая место более отчетливо проявляющимся квантовым свойствам. Это видно, например, из существования «красной границы» фотоэффекта и такой же границы для фотохимических реакций.
Р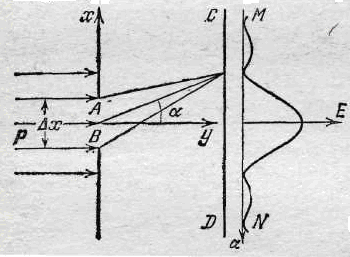 ассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллельный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, расположенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E0·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропорциональная интенсивности I(x) вэтой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)
ассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллельный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, расположенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E0·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропорциональная интенсивности I(x) вэтой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)
E(x) 2.
С квантовой точки зрения образование на экране дифракционной картины означает, что при прохождении света через щель происходит перераспределениефотонов в пространстве. В результате этого в разные точки экрана попадает различноечисло фотонов. Освещенность экрана в данной точке будет тем больше, чем большей будет суммарная энергия фотонов, попадающих за единицу времени в данную точку. Эта энергия, в свою очередь, пропорциональна числу п(x) фотонов, доставивших эту энергию. Таким образом, I(x)
п(x).
Из сказанного следует, что E(x) 2
п(
Формула Планка для испускательной способности АЧТ:

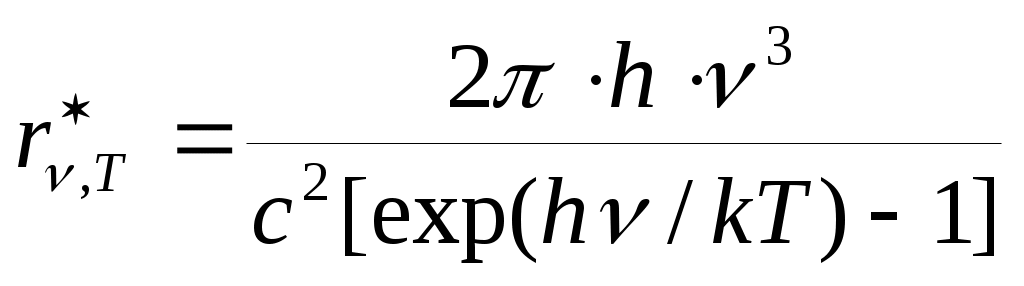
точно согласуется с данными опытов и объясняет все экспериментальные законы теплового излучения тел.
3.4. ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА. ДАВЛЕНИЕ СВЕТА.
Фотоэффект. Классическая теория, представляющая свет как электромагнитные волны, не смогла объяснить законы фотоэффекта и эффект Комптона.
Явлением внешнего фотоэффекта называется вырывание электронов с поверхности тела под действием света достаточно высокой частоты. Экспериментально были установлены следующие закономерности внешнего фотоэффекта:
-
Максимальная кинетическая энергия фотоэлектронов линейно растет с увеличением частоты света и не зависит от его интенсивности.
-
Для каждого вещества существует т.н. «красная граница» фотоэффекта, т.е., наименьшая частота νМИН, при которой еще возможен фотоэффект.
-
Число фотоэлектронов, вырываемых светом из катода за 1с, прямо пропорционально интенсивности света.
-
Фотоэффект практически безынерционен, фототок возникает практически мгновенно после начала освещения катода при условии, что частота света ν ≥ νМИН .
А.Эйнштейн пришел к выводу, что свет распространяется в пространстве и поглощается веществом в виде фотонов – квантов электромагнитного поля с энергией εf = hv.При взаимодействии с веществом фотон целиком передает свою энергию одному электрону. Эта энергия затрачивается на работу выхода электрона из вещества АВЫХ и сообщение вылетевшему электрону кинетической энергии EКИН:
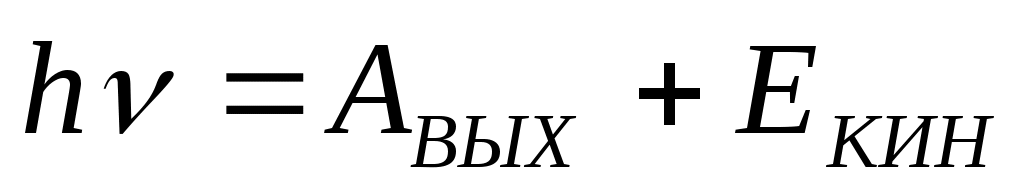 (формула Эйнштейна).
(формула Эйнштейна).
Это выражение объясняет все экспериментальные законы фотоэффекта. В частности, «красную границу» фотоэффекта, т.е., νМИН= АВЫХ/h. Кроме того, фототок прекращается, т.е. электроны не долетают до анода, при приложении между электродами т.н. задерживающей разности потенциалов 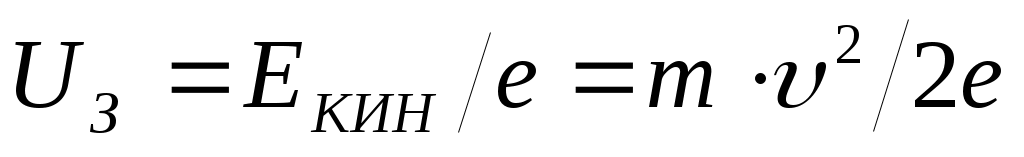 .
.
Эффект Комптона состоит в наблюдении у рассеянного на веществе рентгеновского излучения увеличения длины волны. Он не объясним с волновой точки зрения, т.к. согласно ей при прохождении электромагнитной волны через вещество возникает вторичное излучение с той же самой длиной волны. Этот эффект легко объясняется, если его рассматривать как упругое соударение двух частиц: фотона (f) и неподвижного электрона (e) (рассеяние фотона на электроне) и записать законы сохранения импульса и энергии:
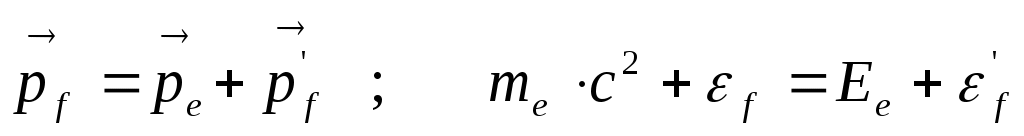 .
.
Учтем, что энергия электрона после столкновения 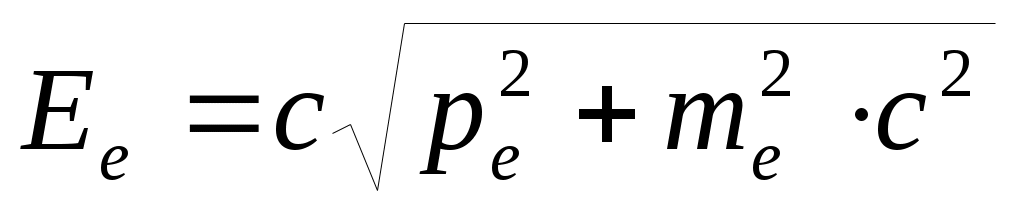 ; εf=hν=hc/λ и εf’=hν’=hc/λ’ – энергии налетающего и рассеянного фотонов, соответственно; θ – угол рассеяния, т.е. угол между векторами импульсов фотонов
; εf=hν=hc/λ и εf’=hν’=hc/λ’ – энергии налетающего и рассеянного фотонов, соответственно; θ – угол рассеяния, т.е. угол между векторами импульсов фотонов 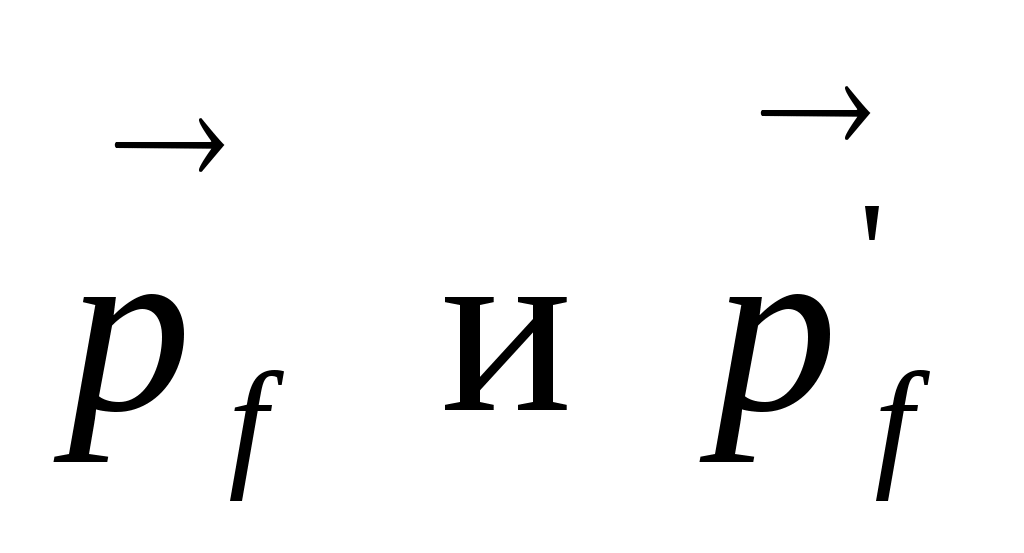 . Так как электромагнитная волна, обладающая энергией Е, имеет импульс р = Е/c(это вытекает из общего выражения СТО для энергии
. Так как электромагнитная волна, обладающая энергией Е, имеет импульс р = Е/c(это вытекает из общего выражения СТО для энергии 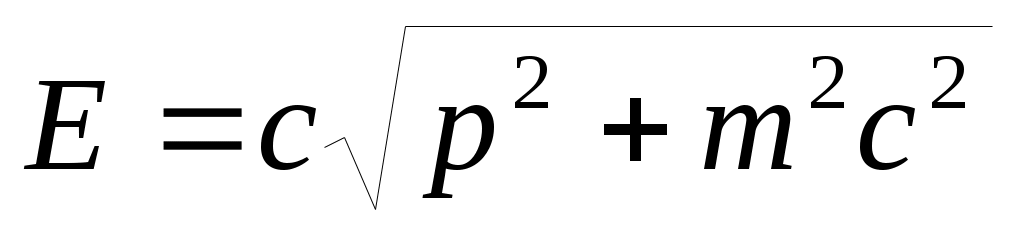 при m= 0), то такое же соотношение должно выполняться и для импульса фотона:pf= εf/c = hv/c=h/λ=ħ·k, где λ и k=2π/λ - длина волны и модуль волнового вектора
при m= 0), то такое же соотношение должно выполняться и для импульса фотона:pf= εf/c = hv/c=h/λ=ħ·k, где λ и k=2π/λ - длина волны и модуль волнового вектора  , соответственно, ħ=h/2π – тоже постоянная Планка.
, соответственно, ħ=h/2π – тоже постоянная Планка.
Решая совместно уравнения получим:
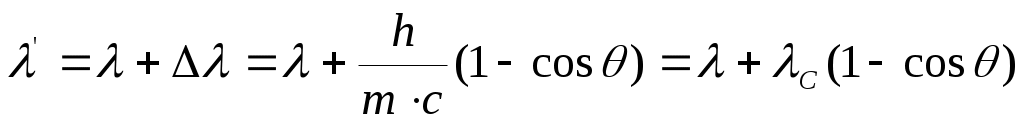 ,
,
где 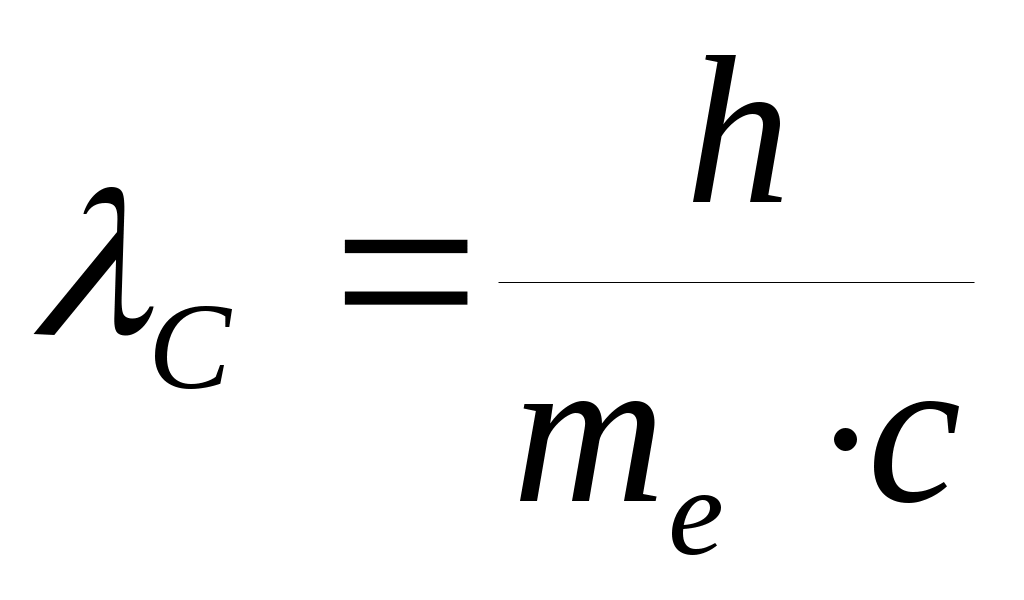 – т.н. комптоновская длина волны для электрона.
– т.н. комптоновская длина волны для электрона.
Рассматривая свет как поток частиц-фотонов удалось также объяснить давление света на поверхность.
Давление света. Фотоны, обладая импульсами, попадая на поверхность, оказывают на нее давление. Если п – плотность фотонов, то на единицу поверхности в единицу времени попадает п·с фотонов. При поглощении каждый фотон сообщает поверхности импульс рf = hv/c, тогда все фотоны сообщат единице площади поверхности в единицу времени импульс (а это и есть давление):
Р =(hv/c)· п·с= εf ·n.
Но величина εf ·nравна энергии фотонов, заключенных в единице объема, т.е., объемной плотности электромагнитной энергии w. Таким образом, Р = wили с учетом того, что часть фотонов отражается: Р = w(1+ ρ), где ρ –коэффициент отражения, равный 1 при полном отражении фотонов, и 0 при их полном поглощении. Полученный результат совпадает с выражением для давления света в электромагнитной теории.
3.5. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ.
Корпускулярно-волновой дуализм света. Т.о., в одних опытах (дифракция, интерференция, поляризация) свет проявляет волновые свойства, в других же (тепловое излучение, фотоэффект, эффект Комптона) он ведет себя как поток частиц-фотонов, но никогда не проявляет волновые и корпускулярные свойства одновременно. Волновая и квантовая теории света дополняют друг друга. Двойственная природа света получила название корпускулярно-волнового дуализма света и находит свое выражение в формулах, определяющих основные характеристики фотонов. Как видно из этих формул, корпускулярные характеристики фотона – энергия εf = hvиимпульс рf = hv/c=h/λ– связаны с волновыми характеристиками света : его частотой ν и длиной волны λ.
Большая группа оптических явлений – интерференция, дифракция, поляризация – полностью объясняется в волновой оптике. Однако, если «перемещаться» от длинных волн в сторону более коротких, то волновые свойства света будут проявляться все слабее, уступая место более отчетливо проявляющимся квантовым свойствам. Это видно, например, из существования «красной границы» фотоэффекта и такой же границы для фотохимических реакций.
Р ассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллельный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, расположенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E0·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропорциональная интенсивности I(x) вэтой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)
ассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллельный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, расположенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E0·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропорциональная интенсивности I(x) вэтой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)
E(x) 2.Максимальная кинетическая энергия фотоэлектронов линейно растет с увеличением частоты света и не зависит от его интенсивности.
Для каждого вещества существует т.н. «красная граница» фотоэффекта, т.е., наименьшая частота νМИН, при которой еще возможен фотоэффект.
Число фотоэлектронов, вырываемых светом из катода за 1с, прямо пропорционально интенсивности света.
Фотоэффект практически безынерционен, фототок возникает практически мгновенно после начала освещения катода при условии, что частота света ν ≥ νМИН .
С квантовой точки зрения образование на экране дифракционной картины означает, что при прохождении света через щель происходит перераспределениефотонов в пространстве. В результате этого в разные точки экрана попадает различноечисло фотонов. Освещенность экрана в данной точке будет тем больше, чем большей будет суммарная энергия фотонов, попадающих за единицу времени в данную точку. Эта энергия, в свою очередь, пропорциональна числу п(x) фотонов, доставивших эту энергию. Таким образом, I(x)
x).Квадрат амплитуды световой волны в какой-либо точке пространства пропорционален числу фотонов, попадающих в эту точку.Иными словами, квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотонов в эту точку.Таким образом, волновые и квантовые свойства света не исключают, а, наоборот, взаимно дополняют друг друга. Квантовые свойства света обусловлены тем, что энергия, импульс и масса излучения сосредоточены в частицах – фотонах. Вероятность нахождения фотонов в различных точках пространства определяется волновыми свойствами света – амплитудой световой волны (квадратом ее модуля).
Далее было установлено, что волновые свойства присущи не только совокупности большого числа одновременно летящих фотонов. Каждый отдельный фотон обладает волновыми свойствами.Волновые свойства фотона проявляются в том, что для него нельзя точно указать, в какую именноточку экрана он попадет после прохождения щели. Можно говорить лишь о вероятности попадания каждого фотонав ту или иную точку экрана.
Такое истолкование связи между волновыми и квантовыми свойствами света сыграло выдающуюся роль в развитии современной физики.
Волновые свойства микрочастиц. Корпускулярно-волновой дуализм присущ не только свету, но и частицам вещества. Эту идею высказал, исходя из соображений симметрии, Луи де Бройль: если свет, который рассматривался как электромагнитная волна, может проявлять корпускулярные свойства, то и частицы вещества должны проявлять волновые свойства.
Согласно этой идее, импульс частицы с массой mи скоростью υ
равен р = mυ, а с другой стороны, он равен p=h/λ. Следовательно, движущейся частице можно поставить в соответствие волну с длиной: λБ=h/p= h/mυ.
Величину λБ называют дебройлевской длиной волны частицы. Экспериментально волновые свойства микрочастиц были обнаружены в опытах по дифракции электронов на кристаллах.
Наличие волновых свойств у частиц вносит ограничения в применимости к ним классической механики, согласно которой частица в любой момент времени занимает определенное положение в пространстве и обладает определенным импульсом.
Когда проводится какое-либо измерение, его результат содержит некоторую неопределенность, обусловленную двумя факторами: корпускулярно-волновым дуализмом и неизбежным взаимодействием наблюдаемого объекта с регистрирующим прибором, приводящим к изменению состояния объекта. Поэтому существует предел, ограничивающий точность измерений. Этот предел не зависит от степени совершенства измерительного прибора, а присущ самой природе вещей. Это и есть принцип неопределенностей Гейзенберга.
Количественные соотношения, выражающие этот принцип для конкретных динамических переменных, называются соотношениями неопределенностей. Наиболее важными являются два из них:
Первое соотношение утверждает, что нельзя измерить одновременно с абсолютной точностью положение (координату) и проекцию импульса микрочастицы на ту же ось. Чем точнее мы пытаемся определить положение объекта, т.е. чем меньше Δх, тем больше будет неопределенность импульса Δрx . Этот вывод можно понять из следующих рассуждений: пусть мы хотим как можно точнее узнать положение микрочастицы (Δх→0 ). Для этого мы должны использовать фотоны с малой длиной волны λ (именно λ определяет точность измерения положения