Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 377
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
граничные условия для решения уравнения Шредингера для частицы внутри потенциальной ямы: 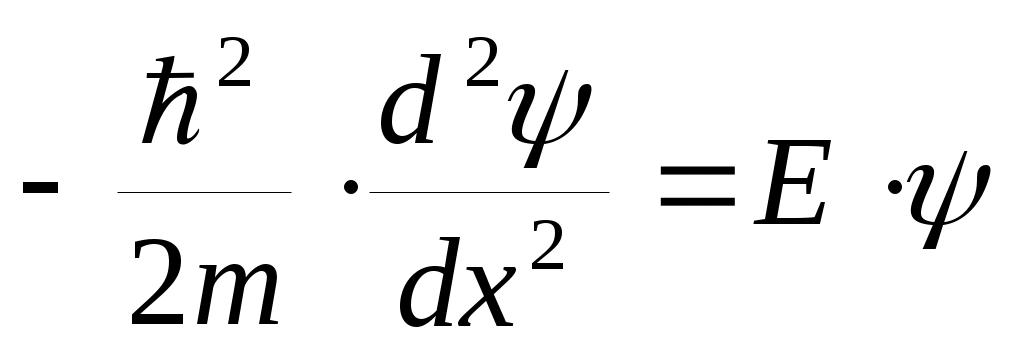 ,
,
где Е — полная энергия частицы.
Решение такого дифференциального уравнения имеет вид:
ψ=A·sin(k·x), где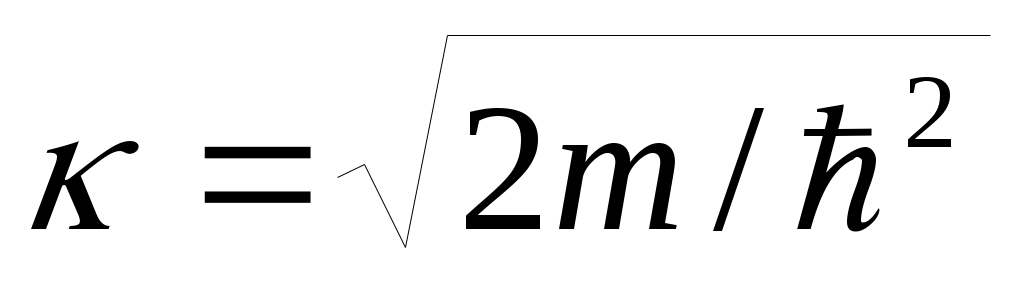 - волновое число.
- волновое число.
Используя граничное условие ψ(ℓ)=0, получим: κn ·ℓ=n·π ,
где n=1,2,3,... – любое целое число, большее нуля (квантовое число). Если учесть, что импульс частицы pn= ħ·kn , то можно найти возможные значения энергии частицы:
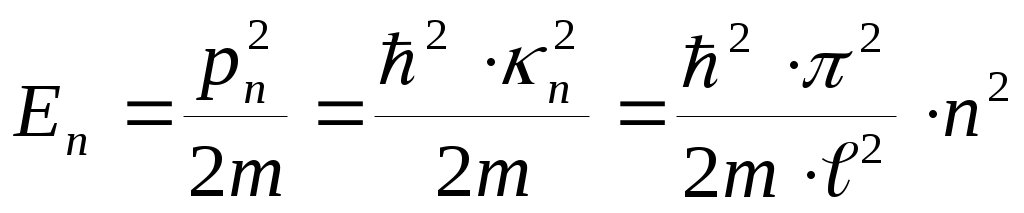 .
.
Уравнение Шредингера имеет решения, удовлетворяющие граничным условиям только при дискретных значениях квантового числа п. Энергия частицы в бесконечно глубокой потенциальной яме оказывается квантованной. Состояние частицы с наименьшей возможной энергией (n=1) называется основным, все остальные состояния – возбужденными. Волновая функция, отвечающая n-му уровню энергии: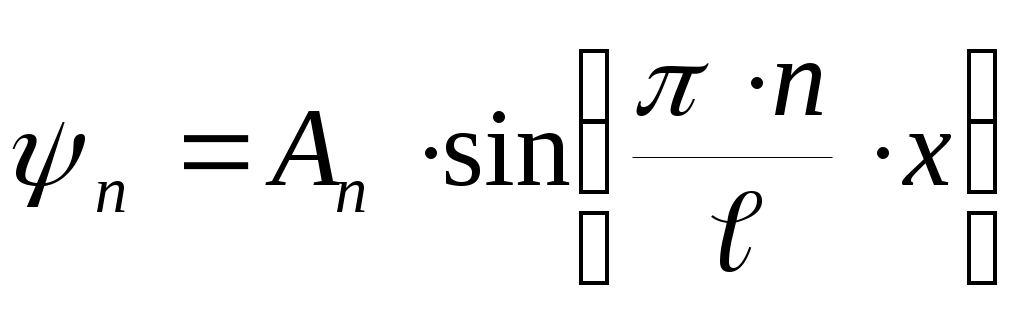 . Постоянную Аnопределим из условия нормировки
. Постоянную Аnопределим из условия нормировки 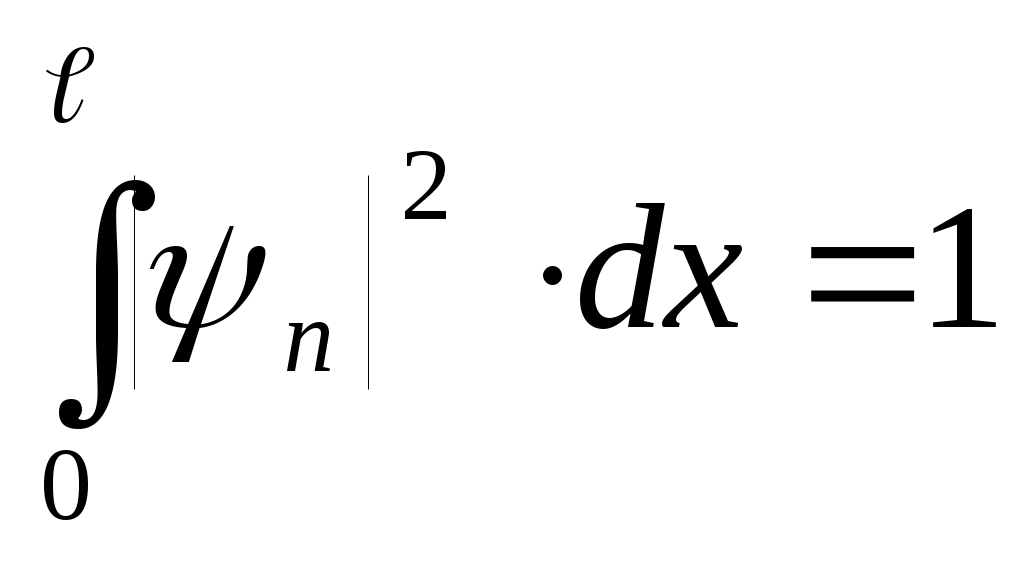 ;
; 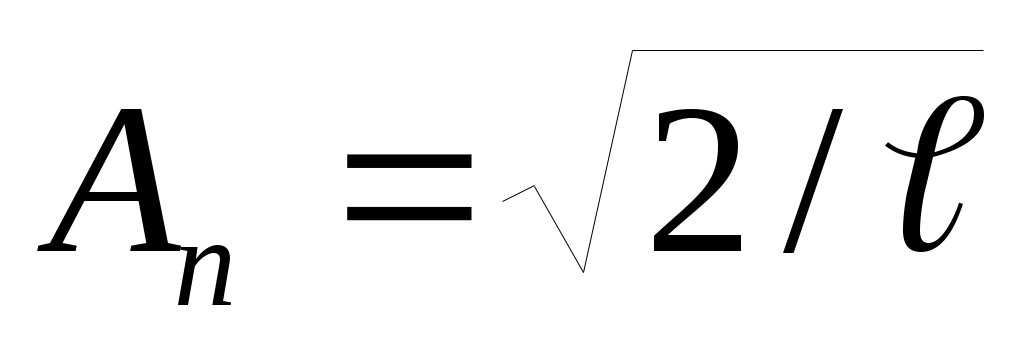 и
и 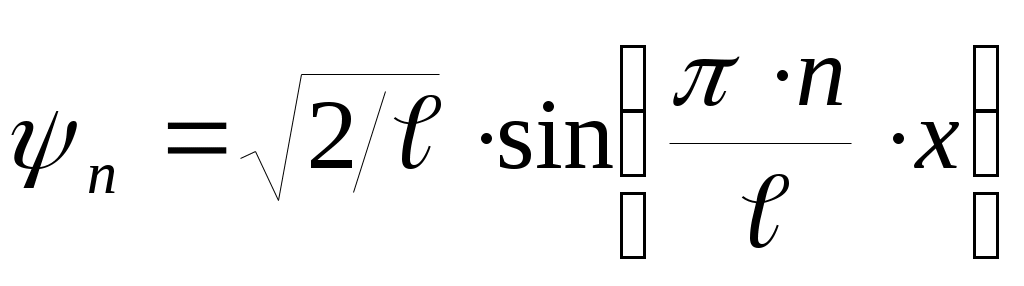 .
.
На границах ямы при х = 0 и х = ℓ всегда |ψn| 2 = 0, однако, вeроятность нахождения частицы в определенной точке внутри ящика может сильно меняться при разных значениях квантового числа
п .
Выводы: энергия микрочастицы, движущейся в потенциальной яме, пробегает дискретный ряд значений; даже в основном состоянии частица не находится в состоянии полного покоя; дискретный характер энергетических уровней проявляется при малой массе частиц и малых размерах области, в которой происходит движение; при больших значениях квантовых чисел и пространственно неограниченном движении квантовомеханические соотношения переходят в формулы классической физики.
Квантовым гармоническим осциллятором называется микрочастица массы т, находящаяся в параболической потенциальной яме вида U(x)=κ·x2/2 и совершающая гармоническое движение с частотой ω;κ-постоянная.
Модель квантового осциллятора особенно полезна при исследовании малых колебаний систем около положения равновесия, например, колебаний атомов в узлах кристаллической решетки или колебаний атомов около их положений равновесия в молекуле.
По аналогии с классической теорией (пружинный маятник) положим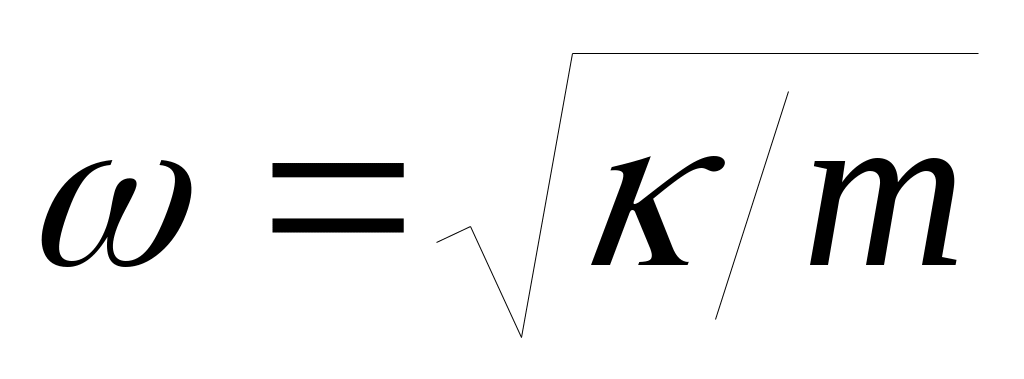 . Тогда для потенциальной энергии получим:
. Тогда для потенциальной энергии получим:
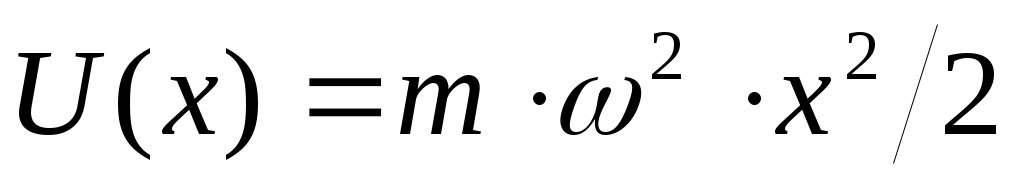 . Стационарное уравнение Шредингера в данном случае будет иметь вид:
. Стационарное уравнение Шредингера в данном случае будет иметь вид:
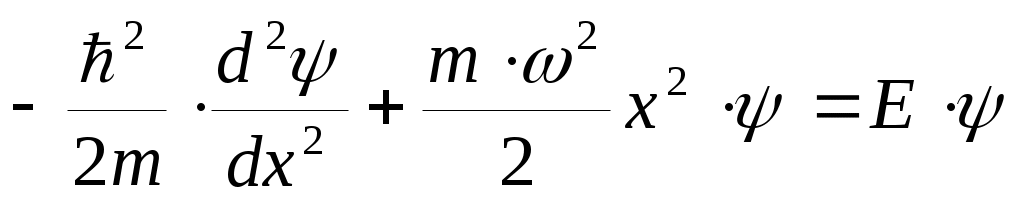 .
.
Полученное уравнение имеет конечные, однозначные и непрерывные решения, т.е. собственные функции, не для всех значений энергии Е, а только при собственных значениях, удовлетворяющих условию: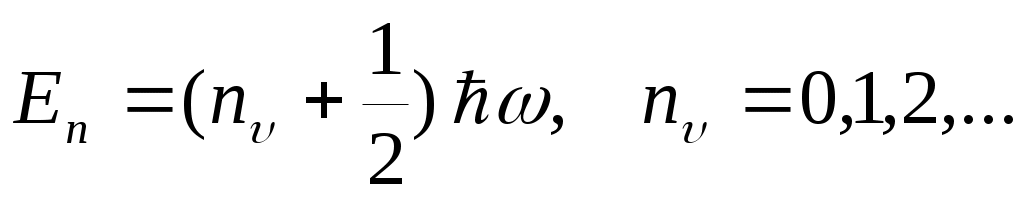
Число nυ называется колебательным квантовым числом. Из последнего равенства следу
ет, что энергия квантового осциллятора квантуется. Энергетический спектр представляет собой эквидистантные, т.е. отстоящие друг от друга на одинаковую величину ΔE=ħω, уровни. Минимальная энергия, которой может обладать квантовый осциллятор, равна Е0 = ħω / 2 и называется энергией нулевых колебаний, или нулевой энергией и соответствует абсолютному нулю температур.
То, что минимальная энергия осциллятора не может быть равна нулю даже при 0К, находится в соответствии с признанием относительности покоя и вечности движения. Если бы энергия частицы равнялась нулю, то это означало бы, что частица покоится и ее импульс и координата одновременно имеют точные значения, что противоречит принципу неопределенностей. Существование нулевых колебаний доказывают опыты по наблюдению рассеяния света прозрачными кристаллами при сверхнизких (вплоть до 10 – 6К) температурах.
Расчет показывает, что для квантового осциллятора возможны переходы только между соседними уровнями, т.е. с изменением квантового числа nυ на единицу:
Δnυ = ±1.
Это условие называется правилом отбора, оно показывает, какие из всех мыслимых переходов реализуются в действительности.
При каждом из переходов излучается или поглощается фотон (или другая частица – фонон) с энергией ħω , где ω – его циклическая частота.
3.6. КВАНТОВАЯ ТЕОРИЯ АТОМА.
Оптические атомные спектры. Известно, что в излучении нагретых тел представлены все длины волн (сплошной спектр).
Если нагреть до достаточно высокой температуры атомарный газ, то в спектре его излучения (спектре испускания) появляются яркие светящиеся линии с определенными дискретными длинами волн. Такие спектры называются линейчатыми. Каждый химический элемент обладает собственным линейчатым спектром.
Простейшим является атом водорода: он состоит из протона и электрона. У водорода самый простой спектр. Дж. Бальмер при изучении видимой части спектра водорода обнаружил четыре спектральные линии с частотами 4,552; 6,173; 6,912 и 7,317 (в 1014 с-1) и показал, что частоты этих линий могут быть рассчитаны по формуле: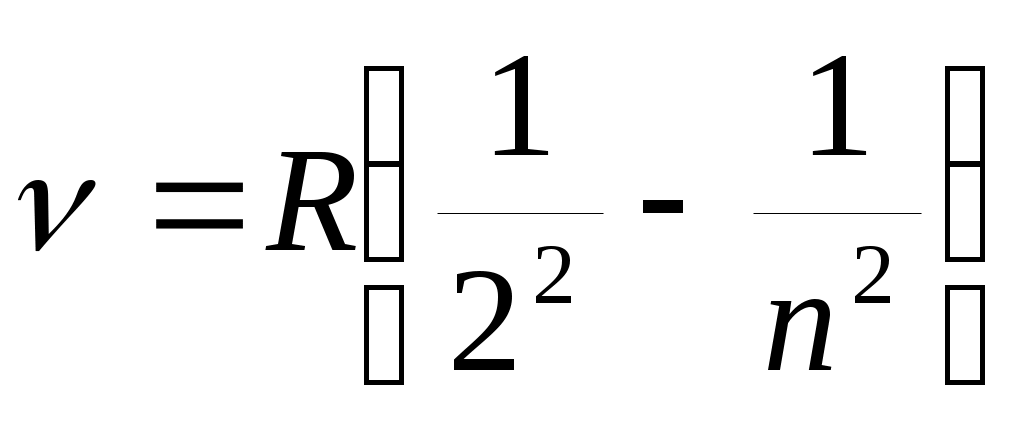 , где для первых четырех линий n принимает значения 3, 4, 5 и 6. R=3,29·1015 c-1 - постоянная Ридберга, была определена экспериментально. Впоследствии были обнаружены линии, соответствующие другим значениям п>6.
, где для первых четырех линий n принимает значения 3, 4, 5 и 6. R=3,29·1015 c-1 - постоянная Ридберга, была определена экспериментально. Впоследствии были обнаружены линии, соответствующие другим значениям п>6.
Установлено, что по мере увеличения частоты линии располагаются все ближе и ближе друг к другу и становятся все менее интенсивными. Вблизи линии с частотой 0,8242·1015 с-1 линии сгущаются настолько, что их трудно различить. Эта частота, соответствующая п=∞, называется границей серии, после нее уже не наблюдается отдельных линий, а имеется слабо выраженный сплошной спектр.
Совокупность спектральных линий, обнаруживающих в своей последовательности и в распределении интенсивности описанную выше закономерность, называется спектральной серией.
Наряду с серией Бальмера в спектре атома водорода был обнаружен ряд других серий, представляемых совершенно аналогичными формулами:
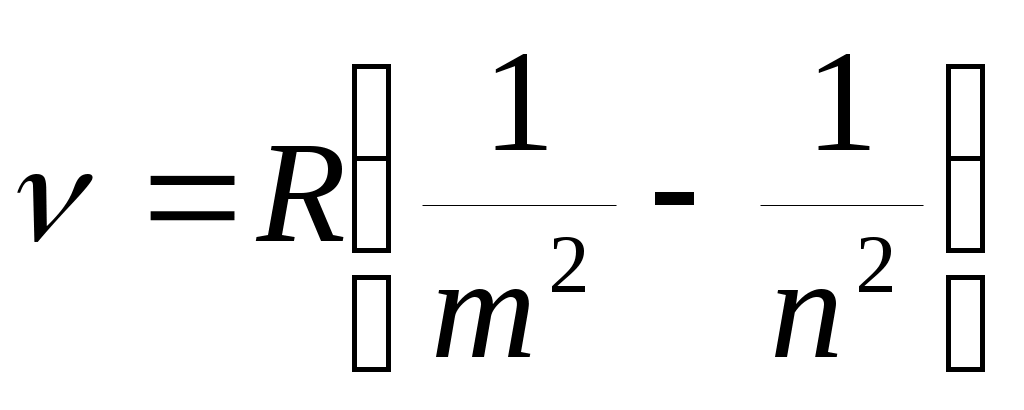 ,
,
m=1,2,3,… n=m+1,m+2,… Это т.н. обобщенная формула Бальмера.
В ультрафиолетовой области Лайман открыл серию линий, частоты которых соответствуют значению m = 1.
В инфракрасной области были обнаружены другие спектральные серии (серии Пашена m= 3, Брэкета m =4, Пфунда m = 5 и т.д.).
Вид этих формул, дискретность частот, определяемую целыми числами n и m, не смогла объяснить классическая физика.
Боровская модель атома водорода. Спектральные серии и устойчивость атома водорода Н.Бор объяснил на основе двух постулатов:
Первый постулат: в атоме существуют такие орбиты, двигаясь по которым электроны энергии не излучают. Эти орбиты называются стационарными.
Второй постулат: при переходе электрона с одной стационарной орбиты на другую испускается или поглощается один фотон, энергия которого (в силу закона сохранения энергии) определяется соотношением : h·νmn=Em – En , где Em и En— энергии электрона в m-ом и n-ом стационарных состояниях.
Стационарными орбитами считаются такие, на которых момент импульса электрона равен целому кратному ħ(условие квантования Бора).
Момент импульса частицы массы т, движущейся по окружности радиусом rсо скоростью υ, равен L= m·υ·r. Поэтому условие квантования Бора имеет вид: m·υ·rn= n·ħ, где n = 1,2,3,... Целое положительное число n называется квантовым числом орбиты, rn– радиус n -ой стационарной орбиты. Условие квантования можно получить, если считать, что на стационарной орбите укладывается целое число волн де Бройля, соответствующих электрону на этой орбите,: 2π·
где Е — полная энергия частицы.
Решение такого дифференциального уравнения имеет вид:
ψ=A·sin(k·x), где
Используя граничное условие ψ(ℓ)=0, получим: κn ·ℓ=n·π ,
где n=1,2,3,... – любое целое число, большее нуля (квантовое число). Если учесть, что импульс частицы pn= ħ·kn , то можно найти возможные значения энергии частицы:
Уравнение Шредингера имеет решения, удовлетворяющие граничным условиям только при дискретных значениях квантового числа п. Энергия частицы в бесконечно глубокой потенциальной яме оказывается квантованной. Состояние частицы с наименьшей возможной энергией (n=1) называется основным, все остальные состояния – возбужденными. Волновая функция, отвечающая n-му уровню энергии:
На границах ямы при х = 0 и х = ℓ всегда |ψn| 2 = 0, однако, вeроятность нахождения частицы в определенной точке внутри ящика может сильно меняться при разных значениях квантового числа
п .
Выводы: энергия микрочастицы, движущейся в потенциальной яме, пробегает дискретный ряд значений; даже в основном состоянии частица не находится в состоянии полного покоя; дискретный характер энергетических уровней проявляется при малой массе частиц и малых размерах области, в которой происходит движение; при больших значениях квантовых чисел и пространственно неограниченном движении квантовомеханические соотношения переходят в формулы классической физики.
Квантовым гармоническим осциллятором называется микрочастица массы т, находящаяся в параболической потенциальной яме вида U(x)=κ·x2/2 и совершающая гармоническое движение с частотой ω;κ-постоянная.
Модель квантового осциллятора особенно полезна при исследовании малых колебаний систем около положения равновесия, например, колебаний атомов в узлах кристаллической решетки или колебаний атомов около их положений равновесия в молекуле.
По аналогии с классической теорией (пружинный маятник) положим
Полученное уравнение имеет конечные, однозначные и непрерывные решения, т.е. собственные функции, не для всех значений энергии Е, а только при собственных значениях, удовлетворяющих условию:
Число nυ называется колебательным квантовым числом. Из последнего равенства следу
ет, что энергия квантового осциллятора квантуется. Энергетический спектр представляет собой эквидистантные, т.е. отстоящие друг от друга на одинаковую величину ΔE=ħω, уровни. Минимальная энергия, которой может обладать квантовый осциллятор, равна Е0 = ħω / 2 и называется энергией нулевых колебаний, или нулевой энергией и соответствует абсолютному нулю температур.
То, что минимальная энергия осциллятора не может быть равна нулю даже при 0К, находится в соответствии с признанием относительности покоя и вечности движения. Если бы энергия частицы равнялась нулю, то это означало бы, что частица покоится и ее импульс и координата одновременно имеют точные значения, что противоречит принципу неопределенностей. Существование нулевых колебаний доказывают опыты по наблюдению рассеяния света прозрачными кристаллами при сверхнизких (вплоть до 10 – 6К) температурах.
Расчет показывает, что для квантового осциллятора возможны переходы только между соседними уровнями, т.е. с изменением квантового числа nυ на единицу:
Δnυ = ±1.
Это условие называется правилом отбора, оно показывает, какие из всех мыслимых переходов реализуются в действительности.
При каждом из переходов излучается или поглощается фотон (или другая частица – фонон) с энергией ħω , где ω – его циклическая частота.
3.6. КВАНТОВАЯ ТЕОРИЯ АТОМА.
Оптические атомные спектры. Известно, что в излучении нагретых тел представлены все длины волн (сплошной спектр).
Если нагреть до достаточно высокой температуры атомарный газ, то в спектре его излучения (спектре испускания) появляются яркие светящиеся линии с определенными дискретными длинами волн. Такие спектры называются линейчатыми. Каждый химический элемент обладает собственным линейчатым спектром.
Простейшим является атом водорода: он состоит из протона и электрона. У водорода самый простой спектр. Дж. Бальмер при изучении видимой части спектра водорода обнаружил четыре спектральные линии с частотами 4,552; 6,173; 6,912 и 7,317 (в 1014 с-1) и показал, что частоты этих линий могут быть рассчитаны по формуле:
Установлено, что по мере увеличения частоты линии располагаются все ближе и ближе друг к другу и становятся все менее интенсивными. Вблизи линии с частотой 0,8242·1015 с-1 линии сгущаются настолько, что их трудно различить. Эта частота, соответствующая п=∞, называется границей серии, после нее уже не наблюдается отдельных линий, а имеется слабо выраженный сплошной спектр.
Совокупность спектральных линий, обнаруживающих в своей последовательности и в распределении интенсивности описанную выше закономерность, называется спектральной серией.
Наряду с серией Бальмера в спектре атома водорода был обнаружен ряд других серий, представляемых совершенно аналогичными формулами:
m=1,2,3,… n=m+1,m+2,… Это т.н. обобщенная формула Бальмера.
В ультрафиолетовой области Лайман открыл серию линий, частоты которых соответствуют значению m = 1.
В инфракрасной области были обнаружены другие спектральные серии (серии Пашена m= 3, Брэкета m =4, Пфунда m = 5 и т.д.).
Вид этих формул, дискретность частот, определяемую целыми числами n и m, не смогла объяснить классическая физика.
Боровская модель атома водорода. Спектральные серии и устойчивость атома водорода Н.Бор объяснил на основе двух постулатов:
Первый постулат: в атоме существуют такие орбиты, двигаясь по которым электроны энергии не излучают. Эти орбиты называются стационарными.
Второй постулат: при переходе электрона с одной стационарной орбиты на другую испускается или поглощается один фотон, энергия которого (в силу закона сохранения энергии) определяется соотношением : h·νmn=Em – En , где Em и En— энергии электрона в m-ом и n-ом стационарных состояниях.
Стационарными орбитами считаются такие, на которых момент импульса электрона равен целому кратному ħ(условие квантования Бора).
Момент импульса частицы массы т, движущейся по окружности радиусом rсо скоростью υ, равен L= m·υ·r. Поэтому условие квантования Бора имеет вид: m·υ·rn= n·ħ, где n = 1,2,3,... Целое положительное число n называется квантовым числом орбиты, rn– радиус n -ой стационарной орбиты. Условие квантования можно получить, если считать, что на стационарной орбите укладывается целое число волн де Бройля, соответствующих электрону на этой орбите,: 2π·