Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 382
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
rn=n·λБ.
Если считать орбиту электрона круговой, то уравнение движения электрона по 2 закону Ньютона: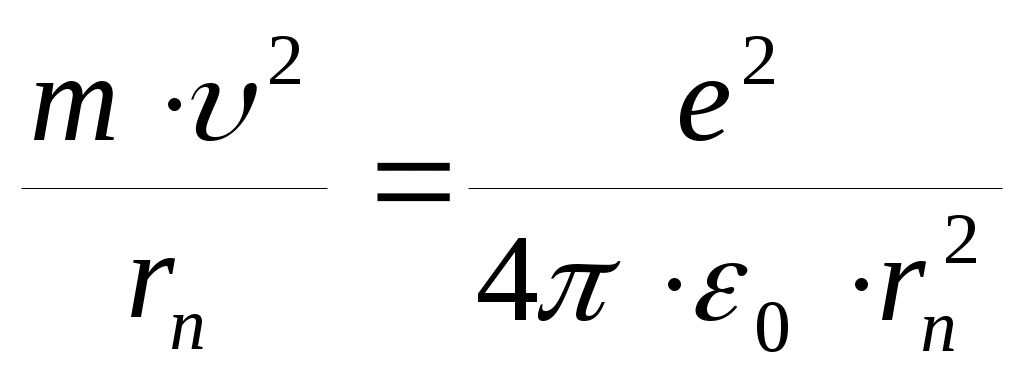 .
.
Решая это уравнение совместно с условием квантования находим для радиуса
n–стационарной орбиты: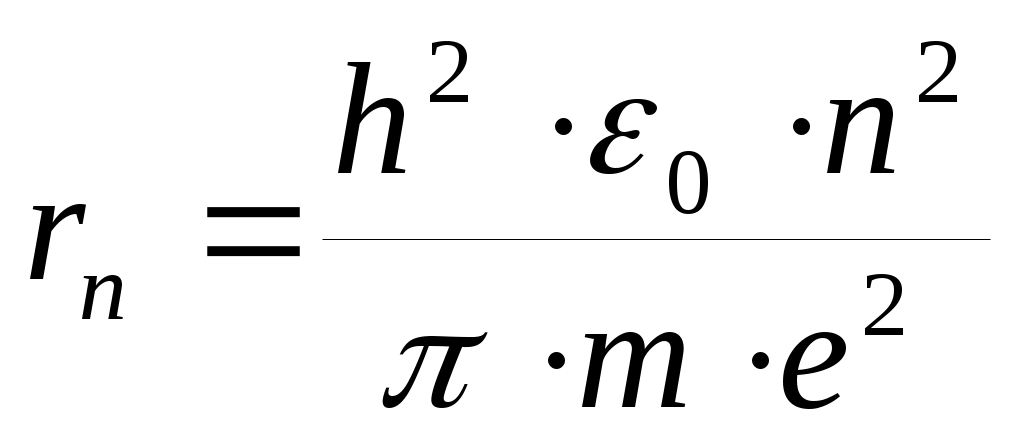 . Радиус ближайшей к ядру орбиты (т.н. первой боровской орбиты с п = 1) равен r1 =0,53·10 - 10м.
. Радиус ближайшей к ядру орбиты (т.н. первой боровской орбиты с п = 1) равен r1 =0,53·10 - 10м.
Полная энергия электрона в атоме водорода равна сумме его кинетической и потенциальной энергий: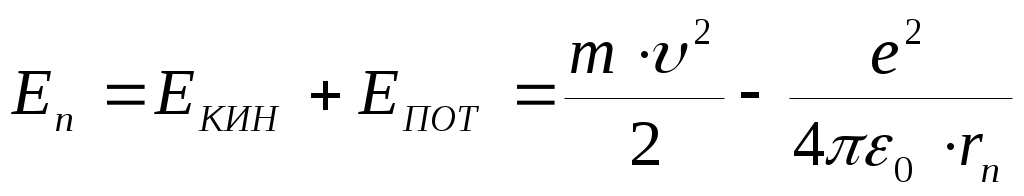 .
.
Решая это уравнение совместно с условиями квантования орбит и радиусов орбит находим для энергии стационарных состояний: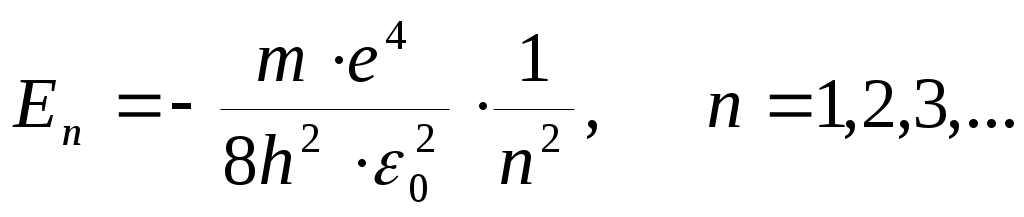 Из последнего соотношения видно, что так же, как и радиусы орбит, энергия электрона квантуется, т.е. принимает ряд дискретных значений. Ближайшая к ядру орбита (n=1) имеет самую низкую энергию (основное состояние):
Из последнего соотношения видно, что так же, как и радиусы орбит, энергия электрона квантуется, т.е. принимает ряд дискретных значений. Ближайшая к ядру орбита (n=1) имеет самую низкую энергию (основное состояние):
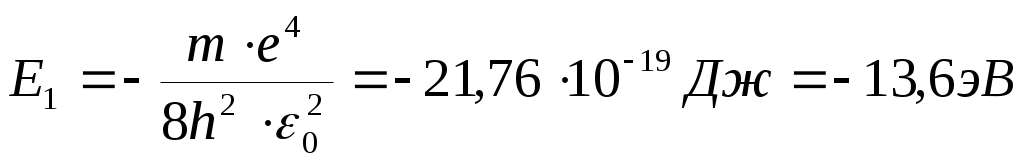 .
.
Энергия, равная 13,6 эВ, необходимая для удаления электрона из атома, называется энергией связи, или энергией ионизации Ei.
При переходе с m–ой орбиты на n–ую испускается фотон с частотой:
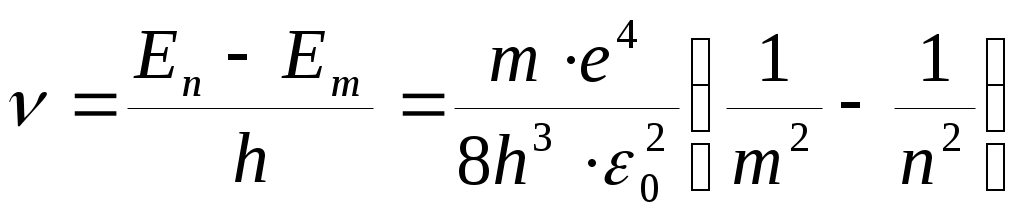 , что совпадает с формулой Бальмера.
, что совпадает с формулой Бальмера.
Множитель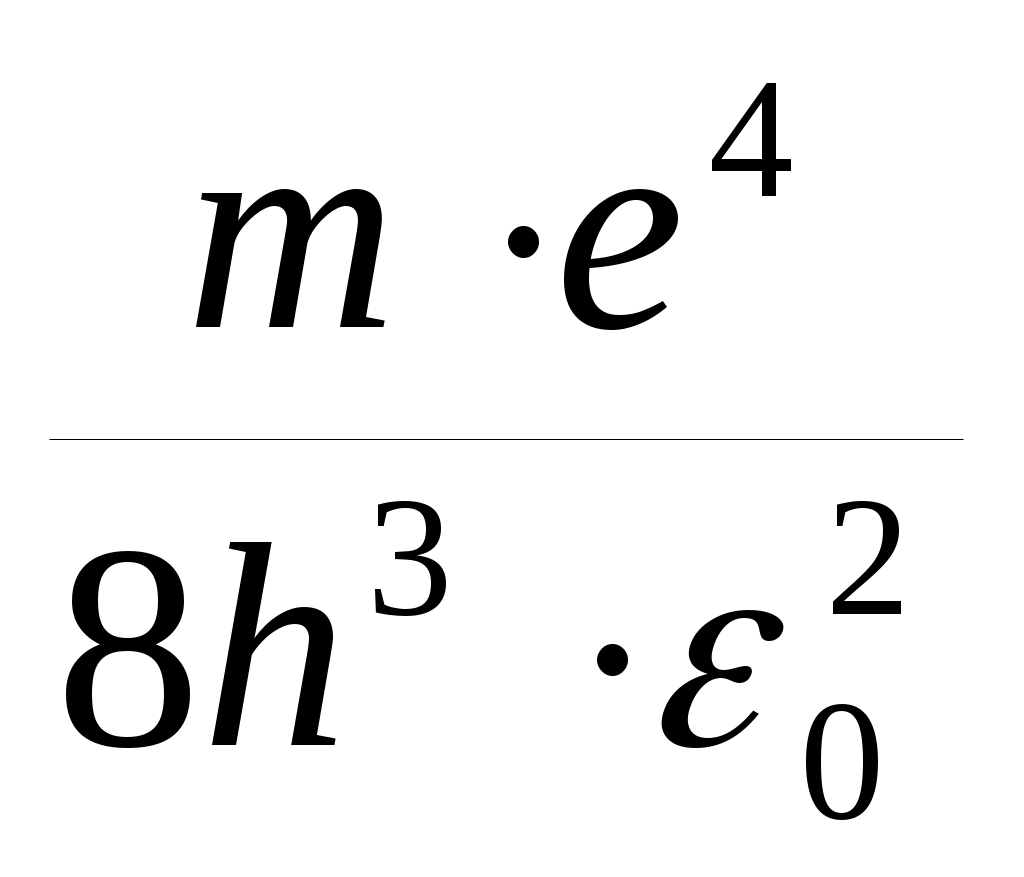 равен 3,29·1015 с-1, что совпадает с постоянной Ридберга.
равен 3,29·1015 с-1, что совпадает с постоянной Ридберга.
Несмотря на успехи, модель атома водорода Бора была непоследовательна, т.к. в ней, с одной стороны, постулируется квантование орбит, а с другой стороны, движение электрона по орбите рассматривается классически.
Атом водорода. Квантовомеханическое рассмотрение. Атом водорода представляет собой один электрон, находящийся в сферически симметричном поле положительно заряженного ядра. Потенциальная энергия взаимодействия электрона и ядра: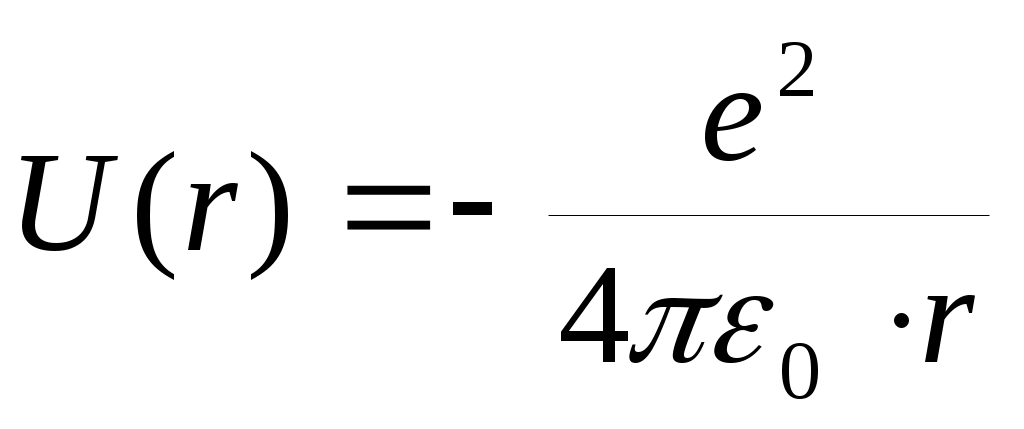 , т.е. можно считать, что электрон движется в гиперболической потенциальной яме. Уравнение Шредингера принимает вид:
, т.е. можно считать, что электрон движется в гиперболической потенциальной яме. Уравнение Шредингера принимает вид: 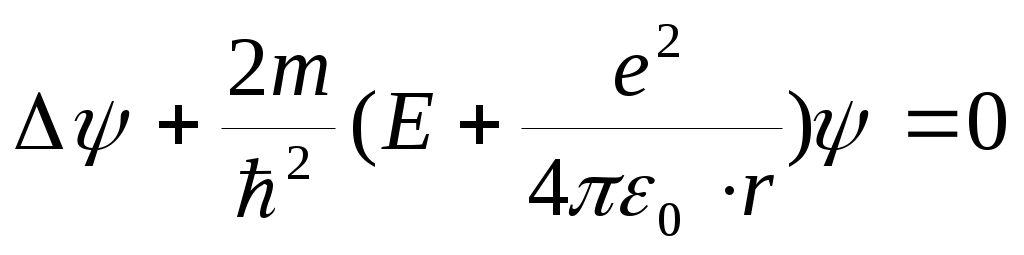 и его удобнее решать в сферической системе координат r, θ и φ. При этом решение ищется в виде произведения трех функций, каждая из которых зависит от одной переменной:
и его удобнее решать в сферической системе координат r, θ и φ. При этом решение ищется в виде произведения трех функций, каждая из которых зависит от одной переменной:
ψ(r,θ,φ) = R(r)·Y (θ)·Ф(φ).
В результате подстановки ψ(r,θ,φ) и разделения переменных уравнение разбивается на три независимых уравнения относительно r, θ и φ, соответственно. Учет физических условий приводит к возможным значениям R{r), Y (θ) и Ф(φ), а следовательно, и ψ -функции. При этом обнаруживается дискретность состояний.
Математически дискретность состояний заключается в том, что каждая из трех функций имеет дискретный набор значений, описываемых соответствующими квантовыми числами:
LSz= mS ·ħ . Правило отбора для спинового квантового числа: ΔmS = 0.
Механическим моментам (орбитальному Lℓи спиновомуLS) соответствуют магнитные моменты, т.к. электрон – заряженная частица. Перечисленные четыре квантовых числа п, ℓ, mℓ и mS полностью описывают состояние электрона в атоме.
Спин. Расчет с помощью уравнения Шредингера энергетического спектра атома водорода показал незначительное расхождение теории с экспериментом. Высокоточные измерения обнаруживают т.н. тонкую структуру уровней энергии – их расщепление на ряд близких подуровней.
Полностью объяснить феномен тонкой структуры смогли лишь на основе такого фундаментального квантово-механического понятия, как спин элементарной частицы. К этому понятию привели результаты опытов О. Штерна и В. Герлаха, еще в 1922 г. наблюдавших расщепление (раздвоение) узкого пучка ато
мов серебра под действием неоднородного магнитного поля. Подобное поведение атомов можно объяснить, лишь предположив, что электрон, кроме орбитального, обладает собственным моментом импульса– спином и связанным с ним собственным магнитным моментом. Такое предположение было сделано в 1925 г. Дж. Уленбеком и С. Гаудсмитом.
Для квантово-механического описания микрочастицы необходимо задать проекцию спина на выбранную ось. Проекция спина может дискретно меняться на величину, кратную ћ. Число проекций равно в общем случае 2s + 1, где s– спиновое число частицы. Так, например, для электрона, имеющего спиновое число s=½ и спин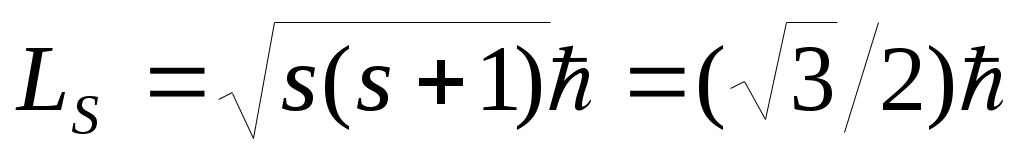 , проекция его спина на выбранную произвольную ось z
, проекция его спина на выбранную произвольную ось z 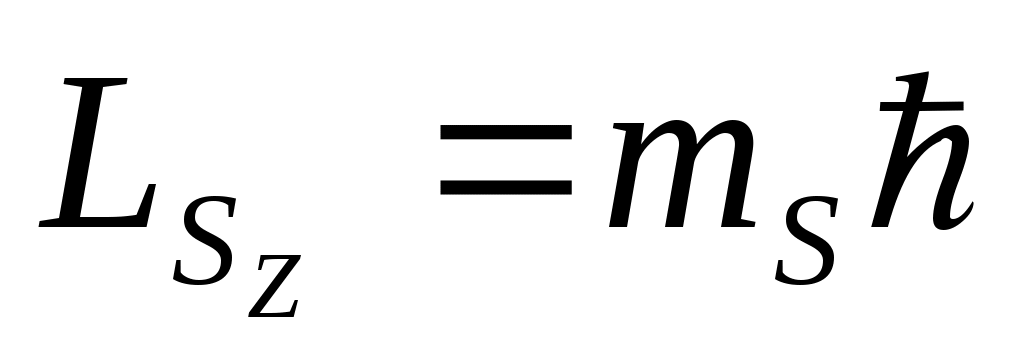 может принимать два значения (mS=±½):
может принимать два значения (mS=±½): 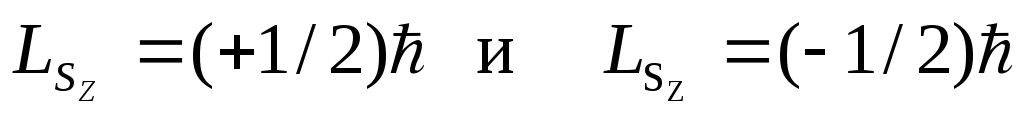 .
.
Значениями спина отличаются два фундаментальных класса элементарных частиц: фермионы имеют полуцелый спин, а бозоны – целочисленный спин. Спин, равный 1/2ћ, имеют электрон, протон, нейтрон, нейтрино, мюон и др. Спин фотона и глюона равен 1ћ, гравитона 2ћ. Спин элементарных частиц лежит в основе квантовой статистики и влияет на поведение систем, состоящих из тождественных частиц. Спин лежит в основе фундаментального принципа квантовой теории – принципа Паули, согласно которому две тождественные частицы с полуцелым спином (фермионы) не могут одновременно находиться в одном и том же квантовом состоянии. Благодаря этому принципу смогли объяснить образование электронных оболочек в атомах и связанную с этим закономерность периодической таблицы Менделеева; формирование ядерных оболочек и их строение; понять химическую связь молекул и многое другое. Со спином связывают появление таких необычных свойств, как сверхтекучесть гелия и сверхпроводимость у некоторых веществ.
Элементы квантовой статистики. Метод, позволяющий перейти от исследования движения отдельных частиц к поведению систем из огромного их числа, называется статистическим. При применении квантовой механики к системам одинаковых частиц были обнаружены свойства, не имеющие классических аналогов. Впервые это стало очевидным при построении теории электронных оболочек многоэлектронных атомов и при рассмотрении равновесного излучения как газа фотонов.
Условия применимости классической статистики – это условия, при которых в движении микрообъектов не проявляются квантовые эффекты. Классические частицы всегда можно различить по их состояниям: координатам и импульсам.
Три основных отличия квантовой статистики от классической:
Бозоны описываются симметричными волновыми функциями ( перестановка двух бозонов не изменяет ни одной из характеристик системы бозонов). К бозонам относятся частицы-переносчики взаимодействия, например, фотоны, глюоны, фононы, гравитоны. В каждом квантовом состоянии может находиться неограниченное количество бозонов. Их распределение по состояниям описывается т.н. статистикой Бозе–Эйнштейна.
Фермионы описываются антисимметричной волновой функцией (при перестановке двух фермионов волновая функция, описывающая систему фермионов, изменяет знак). К фермионам относятся частицы вещества, например, электроны, протоны, нейтроны, кварки и др. Они подчиняются
Если считать орбиту электрона круговой, то уравнение движения электрона по 2 закону Ньютона:
Решая это уравнение совместно с условием квантования находим для радиуса
n–стационарной орбиты:
Полная энергия электрона в атоме водорода равна сумме его кинетической и потенциальной энергий:
Решая это уравнение совместно с условиями квантования орбит и радиусов орбит находим для энергии стационарных состояний:
Энергия, равная 13,6 эВ, необходимая для удаления электрона из атома, называется энергией связи, или энергией ионизации Ei.
При переходе с m–ой орбиты на n–ую испускается фотон с частотой:
Множитель
Несмотря на успехи, модель атома водорода Бора была непоследовательна, т.к. в ней, с одной стороны, постулируется квантование орбит, а с другой стороны, движение электрона по орбите рассматривается классически.
Атом водорода. Квантовомеханическое рассмотрение. Атом водорода представляет собой один электрон, находящийся в сферически симметричном поле положительно заряженного ядра. Потенциальная энергия взаимодействия электрона и ядра:
ψ(r,θ,φ) = R(r)·Y (θ)·Ф(φ).
В результате подстановки ψ(r,θ,φ) и разделения переменных уравнение разбивается на три независимых уравнения относительно r, θ и φ, соответственно. Учет физических условий приводит к возможным значениям R{r), Y (θ) и Ф(φ), а следовательно, и ψ -функции. При этом обнаруживается дискретность состояний.
Математически дискретность состояний заключается в том, что каждая из трех функций имеет дискретный набор значений, описываемых соответствующими квантовыми числами:
-
главное квантовое число п = 1,2,3....
Это число определяет уровни энергии Enэлектрона в атоме водорода : , что совпадает с выражением, полученным в модели атома Бора;
, что совпадает с выражением, полученным в модели атома Бора; -
орбитальное квантовое число ℓ = 0,1,2,. ..(n –1) – определяет геометрическую форму разрешенной для электрона области – орбиталь. Это число ℓ определяет значение орбитального момента импульса Lℓ электрона относительно ядра: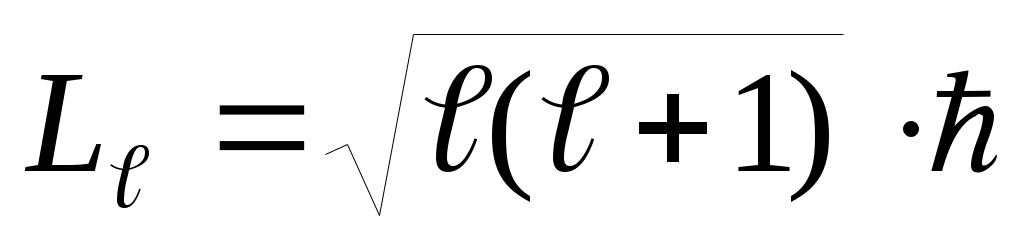 . При переходах из одного состояния в другое ℓ изменяется в соответствии с правилом отбора Δℓ = ±1. Правило отбора по квантовому числу ℓ обусловлено законом сохранения момента импульса.
. При переходах из одного состояния в другое ℓ изменяется в соответствии с правилом отбора Δℓ = ±1. Правило отбора по квантовому числу ℓ обусловлено законом сохранения момента импульса.
-
магнитное квантовое число mℓ = 0, ±1,±2,... ±ℓ, всего 2ℓ + 1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое выделенное направление z: Lℓz =mℓ ·ħ. По другому, оно определяет ориентацию в пространстве орбитали. Правило отбора: Δmℓ =0,±1; -
спиновое квантовое число mS , которое получается не из уравнения Шредингера, а из совокупности опытных данных. Это число может принимать только два значения (±½) и определяет возможные значения проекции LSZ на ось z собственного спинового момента импульса LS электрона: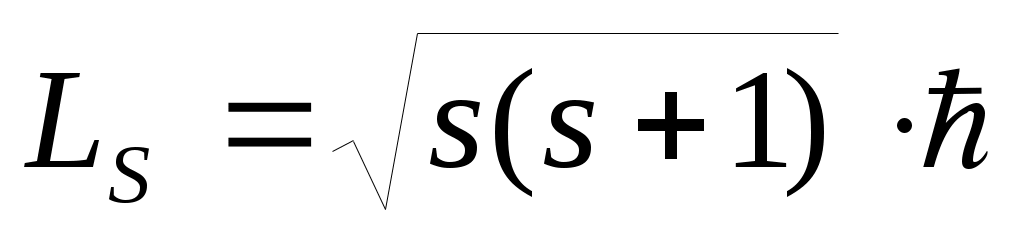 ; s = ½ ;
; s = ½ ;
LSz= mS ·ħ . Правило отбора для спинового квантового числа: ΔmS = 0.
Механическим моментам (орбитальному Lℓи спиновомуLS) соответствуют магнитные моменты, т.к. электрон – заряженная частица. Перечисленные четыре квантовых числа п, ℓ, mℓ и mS полностью описывают состояние электрона в атоме.
Спин. Расчет с помощью уравнения Шредингера энергетического спектра атома водорода показал незначительное расхождение теории с экспериментом. Высокоточные измерения обнаруживают т.н. тонкую структуру уровней энергии – их расщепление на ряд близких подуровней.
Полностью объяснить феномен тонкой структуры смогли лишь на основе такого фундаментального квантово-механического понятия, как спин элементарной частицы. К этому понятию привели результаты опытов О. Штерна и В. Герлаха, еще в 1922 г. наблюдавших расщепление (раздвоение) узкого пучка ато
мов серебра под действием неоднородного магнитного поля. Подобное поведение атомов можно объяснить, лишь предположив, что электрон, кроме орбитального, обладает собственным моментом импульса– спином и связанным с ним собственным магнитным моментом. Такое предположение было сделано в 1925 г. Дж. Уленбеком и С. Гаудсмитом.
Для квантово-механического описания микрочастицы необходимо задать проекцию спина на выбранную ось. Проекция спина может дискретно меняться на величину, кратную ћ. Число проекций равно в общем случае 2s + 1, где s– спиновое число частицы. Так, например, для электрона, имеющего спиновое число s=½ и спин
Значениями спина отличаются два фундаментальных класса элементарных частиц: фермионы имеют полуцелый спин, а бозоны – целочисленный спин. Спин, равный 1/2ћ, имеют электрон, протон, нейтрон, нейтрино, мюон и др. Спин фотона и глюона равен 1ћ, гравитона 2ћ. Спин элементарных частиц лежит в основе квантовой статистики и влияет на поведение систем, состоящих из тождественных частиц. Спин лежит в основе фундаментального принципа квантовой теории – принципа Паули, согласно которому две тождественные частицы с полуцелым спином (фермионы) не могут одновременно находиться в одном и том же квантовом состоянии. Благодаря этому принципу смогли объяснить образование электронных оболочек в атомах и связанную с этим закономерность периодической таблицы Менделеева; формирование ядерных оболочек и их строение; понять химическую связь молекул и многое другое. Со спином связывают появление таких необычных свойств, как сверхтекучесть гелия и сверхпроводимость у некоторых веществ.
Элементы квантовой статистики. Метод, позволяющий перейти от исследования движения отдельных частиц к поведению систем из огромного их числа, называется статистическим. При применении квантовой механики к системам одинаковых частиц были обнаружены свойства, не имеющие классических аналогов. Впервые это стало очевидным при построении теории электронных оболочек многоэлектронных атомов и при рассмотрении равновесного излучения как газа фотонов.
Условия применимости классической статистики – это условия, при которых в движении микрообъектов не проявляются квантовые эффекты. Классические частицы всегда можно различить по их состояниям: координатам и импульсам.
Три основных отличия квантовой статистики от классической:
-
квантовая механика – статистическая теория. Состояние квантовой системы определяется вероятностными законами распределения; -
в квантовой механике многие физические величины могут принимать лишь дискретный ряд значений, в классической механике они непрерывны; -
наиболее важное отличие классической и квантовой статистик связано с принципом тождественности, имеющим место только в квантовой механике. Поскольку в силу принципа неопределенностей понятие траектории частицы утрачивает смысл, то и различить частицы одинаковой природы невозможно, т.е. частицы становятся тождественными. Кроме того, системы частиц с целым (бозоны) и полуцелым (фермионы) спином подчиняются разным законам.
Бозоны описываются симметричными волновыми функциями ( перестановка двух бозонов не изменяет ни одной из характеристик системы бозонов). К бозонам относятся частицы-переносчики взаимодействия, например, фотоны, глюоны, фононы, гравитоны. В каждом квантовом состоянии может находиться неограниченное количество бозонов. Их распределение по состояниям описывается т.н. статистикой Бозе–Эйнштейна.
Фермионы описываются антисимметричной волновой функцией (при перестановке двух фермионов волновая функция, описывающая систему фермионов, изменяет знак). К фермионам относятся частицы вещества, например, электроны, протоны, нейтроны, кварки и др. Они подчиняются