Файл: Мазмны Кiрiспе 1 тарау. Геометриялы салулар теориясыны кейбiр мселелерi 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 225
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
PK.
 1, сондықтан МК РК. Олай болса, ω8 ∩ ω9 = S нүктесі табылады. Қалған салу қадамдары да бірмәнді. Сонымен көрсетілген тәсілмен шешілген есептің жалғыз шешеімі бар және басқа әдіспен шешкенде өзге шешімнің болуы мүмкін емес, өйткені үшбұрышқа тек бір ғана шеңбер іштей сызылады.
1, сондықтан МК РК. Олай болса, ω8 ∩ ω9 = S нүктесі табылады. Қалған салу қадамдары да бірмәнді. Сонымен көрсетілген тәсілмен шешілген есептің жалғыз шешеімі бар және басқа әдіспен шешкенде өзге шешімнің болуы мүмкін емес, өйткені үшбұрышқа тек бір ғана шеңбер іштей сызылады.
Ескерту: MN = 2r, яғни MN = d екенін дәлелдейік (9-сурет). Салу бойынша BC = BN болғандықтан, ВТ1 - әрі медиана, әрі биссектриса, әрі биіктік, онда ВТ1 – CN кесіндісінің орта перпендикуляры, яғни СТ1 = T1N. Онда СВNT1 төртбұрышында BN + CT1 = BC + T1N, яғни ω - СВNT1 төртбұрышына іштей сызылған, онда Т1N – жанама. Дәл осылайша Т2М түзуі де ω шеңберіне жанама болады. Енді Т1N Т2М екенін дәлелдейік. Т1 в және СТ1 ВС болғандықтан, Т1 нүктесінен АВ–ға дейінгі қашықтық СТ1 болады. Ал дәлелдеу бойынша СТ1 = T1N, онда T1N MN. Дәл осылайша Т2М MN. Сонда соңғы екі қатынастан Т1N Т2М, онда MN = d.
ІІ тарау. Салу есептерін шешу әдістері
Салу есептерін шешудің бірнеше әдістері бар. Оларға НГО (нүктелердің геометриялық орны) әдісі, түрлендірулер әдісі (параллель көшіру, осьтік симметрия, центрлік симметрия, бұру, ұқсас түрлендіру, гомотетия), алгебралық әдіс және инверсия әдісі жатады.
§1. НГО әдісі
1.1. НГО ұғымы
Геометриялық фигура әр түрлі тәсілмен беріледі: фигуралардың қиылысуы немесе бірігуі түрінде; фигураны анықтайтын қасиеттердің көрсетілуі арқылы; т.б.. Мысалы, АВ кесіндісі (11-сурет)
шеңберінің диаметрі
берінің хордаларының орталарының
жиыны түрінде берілуі мүмкін.
Егер фигура әрбір нүктесінің қасиетін көрсету арқылы берілсе, онда оны көрсетілген қасиетті қанағаттандыратын НГО деп, ал берілген қасиетті НГО-ң характеристикалық қасиеті деп атайды. Жоғардағы мысалда АВ кесіндісі р түзуіне параллель шеңберінің хордаларының орталарының геометриялық орны болып табылады.
Салу есептерін шешуде пайдаланылатын геометриялық орындар әдісінің мәнісі мынада: айталық, салу есебін шешкенде екі шартты бірдей қанағаттандыратын Х нүктесін табу керек болсын. Бірінші шартты қанағат-тандыратын нүктелердің геометриялық орны қайсыбір Ғ1 фигурасы болады, ал екінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ2 фигурасы болады. Ізделінді Х нүктесі Ғ1 фигурасына да, Ғ2 фигурасына да тиісті, яғни олардың қиылысу нүктесі болып табылады. Егер бұл гео-метриялық орындар қарапайым болса (мысалы, түзулер мен шеңберлерден құралса), біз оларды сала аламыз және қажетті Х нүктесін тауып алуға болады.
НГО сызық немесе бірнеше сызықтардың бірігуі ғана емес, сонымен қатар нүктелердің жиыны, жазықтықтың бөлігі, т.б. болу мүмкін. Кейде көрсетілген қасиетті қанағаттандыратын НГО болмайды.
Ф фигурасы көрсетілген қасиетті қанағаттандыратын НГО екенін дәлелдеу үшін төмендегі өзара қарама - қарсы екі сөйлемді дәлелдеу керек:
1. Ф фигурасының әр нүктесі көрсетілген қасиетке ие болады
2. Көрсетілген қасиетті қанағаттандыратын әрбір нүкте Ф фигурасына тиісті.
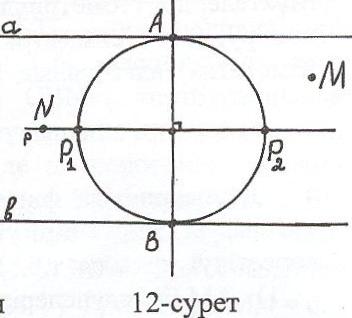
Мысал: Параллель а,в түзулері және оларға перпендикуляр с түзуі берілген. Осы үш түзуден бірдей қашықтықта жататын жазықтық нүктелерінің гео-метриялық орнын анықта.
Шешуі: Айталық а с А, в с В (12-сурет). АВ кесіндісінің ортасы арқылы р а (р в) болатындай р түзуін жүргізіп, осы түзуден с түзуінің екі жағыннан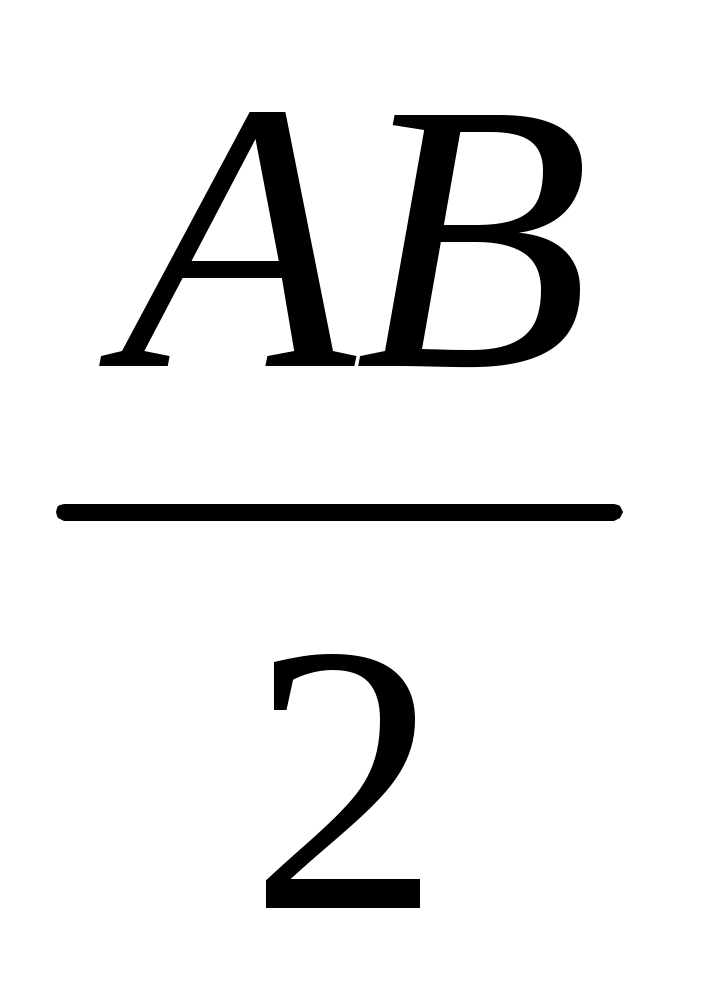
қашықтықтағы нүктелерді Р1, Р2 деп белгілейміз.
С
онда Р1, Р2 нүктелерінің әрқайсысы беріл-
ген түзулерден бірдей қашықтықта жатады.
Жазықтықта осы қасиетті қанағаттандыратын
басқа нүктелер жоқ. Шынында да М нүктесі р
түзуінде жатпайды, сондықтан ол а,в түзулері-
нен бірдей қашықтықта болмайды; N нүктесі
р түзуіне тиісті, бірақ Р1, Р2 нүктелерімен беттеспейді, онда ол а, с түзулерінен бірдей қашықтықта емес. Олай болса, Р1, Р2 нүктелерінің қосы а, в, с түзулерінен бірдей қашықтықтағы НГО болып табылады.
1.2. Қарапайым НГО
Геометриялық салуларда кездесетін қарапайым НГО-ның мысалдары:
1. Берілген екі нүктеден бірдей қашықтықтағы НГО берілген нүктелерді қосатын кесіндінің орта перпендикуляры болады. Бұл НГО кейде берілген нүктелердің симметриясы немесе медиатриссасы деп аталады.
2. Берілген түзуден берілген қашықтықтағы НГО берілген түзуге параллель және әрқайсысы одан берілген қашықтықта жататын түзулердің қосы болады. Оны салу үшін берілген түзуге кез-келген перпендикуляр тұрғызып, оның бойынан берілген түзуден берілген қашықтықта екі нүкте белгілейміз.Сол нүктелер арқылы өтіп берілген түзулерге параллель болатын түзулер ізделінді НГО болады.
3. Берілген екі параллель түзуден бірдей қашықтықтағы НГО берілген түзулердің симметрия осі болады, оны орта сызық, деп те атайды. Бұл НГО-ны салу үшін берілген а, в түзулерін қиятын кез-келген с түзуін жүргізіп, оның берілген түзулер арасындағы кесіндісінің ортасы арқылы а-ға (немесе в-ға) параллель түзу жүргіземіз.
4. Жазықтықтың қиылысушы екі түзуінен бірдей қашықтықтағы НГО берілген түзулер құрайтын бұрыштардың өзара перпендикуляр екі биссектрисасы болады. Оны салу қарапайым бұрышты тең екіге бөлу есебіне келеді.
5. АВ кесіндісінен тік бұрыш арқылы көрінетін НГО АВ диаметрі болатын шеңберді құрайды. Оны салу үшін АВ кесіндісінің ортасы центрі, АВ/2 радиусы болатын шеңбер жүргіземіз.
6. АВ кесіндісі берілген φ бұрышымен (φ ≠ 900 және φ ≠ 1800) көрінетіндей НГО ұштары А, В нүктелері (А, В нүктелерінсіз) болатын, АВ түзуіне қарағанда симметриялы екі доға болады.
7. Берілген шеңбер φ бұрышымен (φ ≠ 1800) көрінетін НГО радиусы берілген шеңбер радиусынан үлкен және берілген шеңберге концентрлі шеңберлер болады.
8. Берілген нүктеден берілген қашықтықтағы НГО - берілген нүкте центрі, берілген қашықтық радиусы болатын шеңбер.
9. Берілген А, В нүктелерінің әрқайсысына дейінгі қашықтықтарының қатынасы тұрақты және 1-ден өзге болатын НГО центрлері АВ түзуінің бойында жататын шеңберлер болады.
10. Берілген А, В нүктелеріне дейінгі қашықтықтарының қосындысы а2 болатын НГО
- егер 2а2 > АВ2 болса, шеңбер болады және оның центрі АВ кесіндісінің бойында жатады;
- егер 2а2 = АВ2 болса, центрі АВ кесіндісінің ортасында жататын шеңбер болады;
- егер 2а2 < АВ2 болса, құр жиын болады.
11. (О, ОА) шеңберінің А нүктесі арқылы жүргізілген барлық хордаларды берілген λ (λ > 0) қатынасында бөлетін нүктелердің жиыны центрі ОА тү-зуінде жататын және А нүктесі арқылы өтетін (А нүктесінің өзі алынбайды) шеңбер болады.
1.3. НГО іздеу
Геометриялық салулардың ішінде НГО–нын табу есептері жиі кездеседі. Мұндай есептерде кейбір «қарапайым» немесе «элементар» фигуралардың бірігуі белгілі деп алынып, осы бірігудің қай элементі ізделінді ГО–ды қанағаттандыратанын тауып, көрсету керек. НГО табу есептерін шешу методикасы талдау, салу, дәлелдеу және зерттеуден тұрады.
Талдаудың мақсаты – ізделінді НГО–ның қандай болатыны жөнінде болжам жасау. Әдетте, талдауды берілген фигуралардың сызбасын салып, сол сызбадан ізделінді НГО-а тиісті бір нүктені қарастырудан бастайды. Сонан соң осы нүкте мен берілген элементтер арасында ГО–ның формасы мен орналасуын анықтауға мүмкіндік беретіндей қатынас орнатылады. Нәтижесінде тек дәлелдеуді қажет ететін болжам шығады.
Дәлелдеуде өзара қарама - қарсы екі сөйлемнің ақиқаттығы анықталады:
Немесе екінші сөйлемді былайша тұжырымдауға болады:
2') егер қандай да бір нүкте табылған фигураға тиісті болмаса, онда ол
көрсетілген характиристикалық қасиетті қанағаттандырмайды.
Зерттеуде берілген фигуралардың әртүрлі орналасу жағдайларындағы шешімдердің мүмкін болатын мәндері анықталады.
Мысал: Берілген екі нүкте арқылы өтетін шеңберлердің центрлерінің ГО тап.
Шешуі:
Т
алдау.
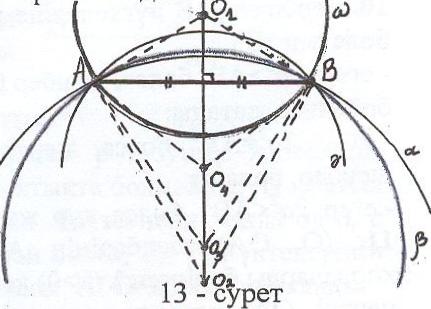
Есеп шешілді делік, яғни А, В – берілген нүктелер, , , , ...-А,В нүктелері арқылы өтетін шеңберлер, ал О1, О2, О3, О4... сәйкесінше осы шеңберлердің центрлері (13-сурет). Бұл нүктелер ізделінді НГО – ның нүктелері. Олар бір түзудің бойында жатады және ол түзу АВ кесіндісінің орта перпендикуляры болады.
Дәлелдеу. О1А және О1В – шеңберінің
радиустары болғандықтан, олар өзара тең
болады. Онда АО1В үшбұрышы теңбүйірлі.
Теңбүйірлі үшбұрыштардың қасиеті бойын-
ша О1 төбесі табанының орта перпендикуля-
рында жатады. Дәл осылайша қалған центр-
лердің АВ кесіндісінің орта перпендикулярына тиістілігі дәлелденеді. Сонда берілген екі нүкте арқылы өтетін шеңберлердің центрлерінің ГО – берілген нүктелерді қосатын кесіндінің орта перпендикуляры болады.
Зерттеу. Егер А, В нүктелері беттеспесе, ізделінді ГО – осы нүктелерді қосатын кесіндінің орта перпендикуляры. Егер А, В нүктелері беттесетін болса, онда ізделінді ГО – бүкіл кеңістік болады, яғни кеңістіктің барлық нүктелері (А,В нүктелерінен басқа) осы ГО – ға тиісті.
1.4. НГО әдісімен шешілетін геометриялық
салуларға мысалдар
Есеп 1: Бір қабырғасы, сол қабырғаға қарсы жатқан сүйір бұрышы және іштей сызылған шеңбердің радиусы бойынша үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш, ВС, ВАС және r берілген элементтер (14 – сурет).
А
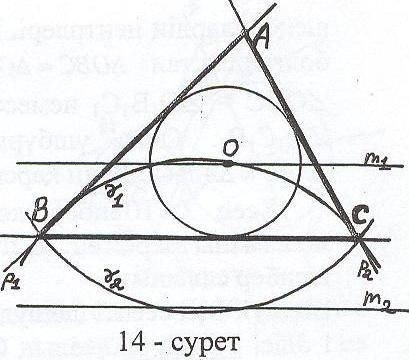
йталық О – іштей сызылған шеңбердің центрі. ВС түзуін кез – келген етіп алып, одан кез – келген ВС кесіндісін белгілеу оңай. Содан соң О нүктесін тұрғызсақ, ізделінді үшбұрыштың А төбесі оңай табылады. Олай болса, О нүктесі негізгі элемент болып табылады.
ВОС үшбұрышынан
ВОС + АВС +
АВС +  АСВ = 1800
АСВ = 1800
ВОС = 1800 - (1800 - A) = 900 -
(1800 - A) = 900 -  A
A
ВОС = 900 - ,
,
мұндағы = ВАС және 90
Ескерту: MN = 2r, яғни MN = d екенін дәлелдейік (9-сурет). Салу бойынша BC = BN болғандықтан, ВТ1 - әрі медиана, әрі биссектриса, әрі биіктік, онда ВТ1 – CN кесіндісінің орта перпендикуляры, яғни СТ1 = T1N. Онда СВNT1 төртбұрышында BN + CT1 = BC + T1N, яғни ω - СВNT1 төртбұрышына іштей сызылған, онда Т1N – жанама. Дәл осылайша Т2М түзуі де ω шеңберіне жанама болады. Енді Т1N Т2М екенін дәлелдейік. Т1 в және СТ1 ВС болғандықтан, Т1 нүктесінен АВ–ға дейінгі қашықтық СТ1 болады. Ал дәлелдеу бойынша СТ1 = T1N, онда T1N MN. Дәл осылайша Т2М MN. Сонда соңғы екі қатынастан Т1N Т2М, онда MN = d.
ІІ тарау. Салу есептерін шешу әдістері
Салу есептерін шешудің бірнеше әдістері бар. Оларға НГО (нүктелердің геометриялық орны) әдісі, түрлендірулер әдісі (параллель көшіру, осьтік симметрия, центрлік симметрия, бұру, ұқсас түрлендіру, гомотетия), алгебралық әдіс және инверсия әдісі жатады.
§1. НГО әдісі
1.1. НГО ұғымы
Геометриялық фигура әр түрлі тәсілмен беріледі: фигуралардың қиылысуы немесе бірігуі түрінде; фигураны анықтайтын қасиеттердің көрсетілуі арқылы; т.б.. Мысалы, АВ кесіндісі (11-сурет)
-
А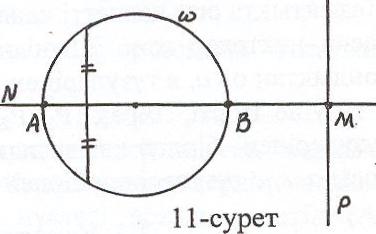
М, ВN сәулелерінің қиылысуы -
р түзуіне перпендикуляр болатын
шеңберінің диаметрі
-
р түзуіне параллель болатын шең-
берінің хордаларының орталарының
жиыны түрінде берілуі мүмкін.
Егер фигура әрбір нүктесінің қасиетін көрсету арқылы берілсе, онда оны көрсетілген қасиетті қанағаттандыратын НГО деп, ал берілген қасиетті НГО-ң характеристикалық қасиеті деп атайды. Жоғардағы мысалда АВ кесіндісі р түзуіне параллель шеңберінің хордаларының орталарының геометриялық орны болып табылады.
Салу есептерін шешуде пайдаланылатын геометриялық орындар әдісінің мәнісі мынада: айталық, салу есебін шешкенде екі шартты бірдей қанағаттандыратын Х нүктесін табу керек болсын. Бірінші шартты қанағат-тандыратын нүктелердің геометриялық орны қайсыбір Ғ1 фигурасы болады, ал екінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ2 фигурасы болады. Ізделінді Х нүктесі Ғ1 фигурасына да, Ғ2 фигурасына да тиісті, яғни олардың қиылысу нүктесі болып табылады. Егер бұл гео-метриялық орындар қарапайым болса (мысалы, түзулер мен шеңберлерден құралса), біз оларды сала аламыз және қажетті Х нүктесін тауып алуға болады.
НГО сызық немесе бірнеше сызықтардың бірігуі ғана емес, сонымен қатар нүктелердің жиыны, жазықтықтың бөлігі, т.б. болу мүмкін. Кейде көрсетілген қасиетті қанағаттандыратын НГО болмайды.
Ф фигурасы көрсетілген қасиетті қанағаттандыратын НГО екенін дәлелдеу үшін төмендегі өзара қарама - қарсы екі сөйлемді дәлелдеу керек:
1. Ф фигурасының әр нүктесі көрсетілген қасиетке ие болады
2. Көрсетілген қасиетті қанағаттандыратын әрбір нүкте Ф фигурасына тиісті.
Мысал: Параллель а,в түзулері және оларға перпендикуляр с түзуі берілген. Осы үш түзуден бірдей қашықтықта жататын жазықтық нүктелерінің гео-метриялық орнын анықта.
Шешуі: Айталық а с А, в с В (12-сурет). АВ кесіндісінің ортасы арқылы р а (р в) болатындай р түзуін жүргізіп, осы түзуден с түзуінің екі жағыннан
қашықтықтағы нүктелерді Р1, Р2 деп белгілейміз.
С

онда Р1, Р2 нүктелерінің әрқайсысы беріл-
ген түзулерден бірдей қашықтықта жатады.
Жазықтықта осы қасиетті қанағаттандыратын
басқа нүктелер жоқ. Шынында да М нүктесі р
түзуінде жатпайды, сондықтан ол а,в түзулері-
нен бірдей қашықтықта болмайды; N нүктесі
р түзуіне тиісті, бірақ Р1, Р2 нүктелерімен беттеспейді, онда ол а, с түзулерінен бірдей қашықтықта емес. Олай болса, Р1, Р2 нүктелерінің қосы а, в, с түзулерінен бірдей қашықтықтағы НГО болып табылады.
1.2. Қарапайым НГО
Геометриялық салуларда кездесетін қарапайым НГО-ның мысалдары:
1. Берілген екі нүктеден бірдей қашықтықтағы НГО берілген нүктелерді қосатын кесіндінің орта перпендикуляры болады. Бұл НГО кейде берілген нүктелердің симметриясы немесе медиатриссасы деп аталады.
2. Берілген түзуден берілген қашықтықтағы НГО берілген түзуге параллель және әрқайсысы одан берілген қашықтықта жататын түзулердің қосы болады. Оны салу үшін берілген түзуге кез-келген перпендикуляр тұрғызып, оның бойынан берілген түзуден берілген қашықтықта екі нүкте белгілейміз.Сол нүктелер арқылы өтіп берілген түзулерге параллель болатын түзулер ізделінді НГО болады.
3. Берілген екі параллель түзуден бірдей қашықтықтағы НГО берілген түзулердің симметрия осі болады, оны орта сызық, деп те атайды. Бұл НГО-ны салу үшін берілген а, в түзулерін қиятын кез-келген с түзуін жүргізіп, оның берілген түзулер арасындағы кесіндісінің ортасы арқылы а-ға (немесе в-ға) параллель түзу жүргіземіз.
4. Жазықтықтың қиылысушы екі түзуінен бірдей қашықтықтағы НГО берілген түзулер құрайтын бұрыштардың өзара перпендикуляр екі биссектрисасы болады. Оны салу қарапайым бұрышты тең екіге бөлу есебіне келеді.
5. АВ кесіндісінен тік бұрыш арқылы көрінетін НГО АВ диаметрі болатын шеңберді құрайды. Оны салу үшін АВ кесіндісінің ортасы центрі, АВ/2 радиусы болатын шеңбер жүргіземіз.
6. АВ кесіндісі берілген φ бұрышымен (φ ≠ 900 және φ ≠ 1800) көрінетіндей НГО ұштары А, В нүктелері (А, В нүктелерінсіз) болатын, АВ түзуіне қарағанда симметриялы екі доға болады.
7. Берілген шеңбер φ бұрышымен (φ ≠ 1800) көрінетін НГО радиусы берілген шеңбер радиусынан үлкен және берілген шеңберге концентрлі шеңберлер болады.
8. Берілген нүктеден берілген қашықтықтағы НГО - берілген нүкте центрі, берілген қашықтық радиусы болатын шеңбер.
9. Берілген А, В нүктелерінің әрқайсысына дейінгі қашықтықтарының қатынасы тұрақты және 1-ден өзге болатын НГО центрлері АВ түзуінің бойында жататын шеңберлер болады.
10. Берілген А, В нүктелеріне дейінгі қашықтықтарының қосындысы а2 болатын НГО
- егер 2а2 > АВ2 болса, шеңбер болады және оның центрі АВ кесіндісінің бойында жатады;
- егер 2а2 = АВ2 болса, центрі АВ кесіндісінің ортасында жататын шеңбер болады;
- егер 2а2 < АВ2 болса, құр жиын болады.
11. (О, ОА) шеңберінің А нүктесі арқылы жүргізілген барлық хордаларды берілген λ (λ > 0) қатынасында бөлетін нүктелердің жиыны центрі ОА тү-зуінде жататын және А нүктесі арқылы өтетін (А нүктесінің өзі алынбайды) шеңбер болады.
1.3. НГО іздеу
Геометриялық салулардың ішінде НГО–нын табу есептері жиі кездеседі. Мұндай есептерде кейбір «қарапайым» немесе «элементар» фигуралардың бірігуі белгілі деп алынып, осы бірігудің қай элементі ізделінді ГО–ды қанағаттандыратанын тауып, көрсету керек. НГО табу есептерін шешу методикасы талдау, салу, дәлелдеу және зерттеуден тұрады.
Талдаудың мақсаты – ізделінді НГО–ның қандай болатыны жөнінде болжам жасау. Әдетте, талдауды берілген фигуралардың сызбасын салып, сол сызбадан ізделінді НГО-а тиісті бір нүктені қарастырудан бастайды. Сонан соң осы нүкте мен берілген элементтер арасында ГО–ның формасы мен орналасуын анықтауға мүмкіндік беретіндей қатынас орнатылады. Нәтижесінде тек дәлелдеуді қажет ететін болжам шығады.
Дәлелдеуде өзара қарама - қарсы екі сөйлемнің ақиқаттығы анықталады:
-
талдауда табылған фигураның кез-келген нүктесі ізделінді НГО-ның характеристикалық қасиетін қанағаттандырады; -
көрсетілген характиристикалық қасиетті қанағаттандыратын әрбір нүкте талдауда табылған фигураға тиісті.
Немесе екінші сөйлемді былайша тұжырымдауға болады:
2') егер қандай да бір нүкте табылған фигураға тиісті болмаса, онда ол
көрсетілген характиристикалық қасиетті қанағаттандырмайды.
Зерттеуде берілген фигуралардың әртүрлі орналасу жағдайларындағы шешімдердің мүмкін болатын мәндері анықталады.
Мысал: Берілген екі нүкте арқылы өтетін шеңберлердің центрлерінің ГО тап.
Шешуі:
Т

алдау.
Есеп шешілді делік, яғни А, В – берілген нүктелер, , , , ...-А,В нүктелері арқылы өтетін шеңберлер, ал О1, О2, О3, О4... сәйкесінше осы шеңберлердің центрлері (13-сурет). Бұл нүктелер ізделінді НГО – ның нүктелері. Олар бір түзудің бойында жатады және ол түзу АВ кесіндісінің орта перпендикуляры болады.
Дәлелдеу. О1А және О1В – шеңберінің
радиустары болғандықтан, олар өзара тең
болады. Онда АО1В үшбұрышы теңбүйірлі.
Теңбүйірлі үшбұрыштардың қасиеті бойын-
ша О1 төбесі табанының орта перпендикуля-
рында жатады. Дәл осылайша қалған центр-
лердің АВ кесіндісінің орта перпендикулярына тиістілігі дәлелденеді. Сонда берілген екі нүкте арқылы өтетін шеңберлердің центрлерінің ГО – берілген нүктелерді қосатын кесіндінің орта перпендикуляры болады.
Зерттеу. Егер А, В нүктелері беттеспесе, ізделінді ГО – осы нүктелерді қосатын кесіндінің орта перпендикуляры. Егер А, В нүктелері беттесетін болса, онда ізделінді ГО – бүкіл кеңістік болады, яғни кеңістіктің барлық нүктелері (А,В нүктелерінен басқа) осы ГО – ға тиісті.
1.4. НГО әдісімен шешілетін геометриялық
салуларға мысалдар
Есеп 1: Бір қабырғасы, сол қабырғаға қарсы жатқан сүйір бұрышы және іштей сызылған шеңбердің радиусы бойынша үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш, ВС, ВАС және r берілген элементтер (14 – сурет).
А

йталық О – іштей сызылған шеңбердің центрі. ВС түзуін кез – келген етіп алып, одан кез – келген ВС кесіндісін белгілеу оңай. Содан соң О нүктесін тұрғызсақ, ізделінді үшбұрыштың А төбесі оңай табылады. Олай болса, О нүктесі негізгі элемент болып табылады.
ВОС үшбұрышынан
ВОС +
ВОС = 1800 -
ВОС = 900 -
мұндағы = ВАС және 90