Файл: Мазмны Кiрiспе 1 тарау. Геометриялы салулар теориясыны кейбiр мселелерi 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 218
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
с
теңсіздіктері орындалғанда ғана мүмкін болады. Ал 3) – 7) салу қадамдары әрқашан орындалады. Олай болса, бір уақытта hв 2mа және hс 2mа теңсіздіктері орындалғанда есептің жалғыз шешуі бар. Басқа тәсілмен шешкенде өзге шешім шығуы мүмкін емес, себебі mа = mа, hc = hc, hв = hв ∆АВС = ∆АВС.
Есеп 3: р периметрі мен іргелес , бұрыштары бойынша үшбұрыш салу.
Шешуі:
Талдау: Айталық ВС – ізделінді үшбұрыш (4 - сурет),
А
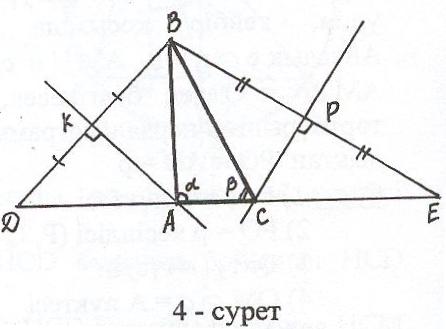
В + ВС + СА = р
және ВАС = , ВСА = .
Егер АС табанының созындысына АD = AB,
CE = BC болатындай кесінділер белгілесек,
DE кесіндісінің ұзындығы периметрге тең
болады, яғни DE = p. D, E нүктелерін АВС
үшбұрышының В төбесімен қосамыз.
Сонда DBA және EBC тең бүйірлі үшбұрыш-
тары шығады. Үшбұрыштың сыртқы бұрышының қасиетін ескерсек, ADB = ABD =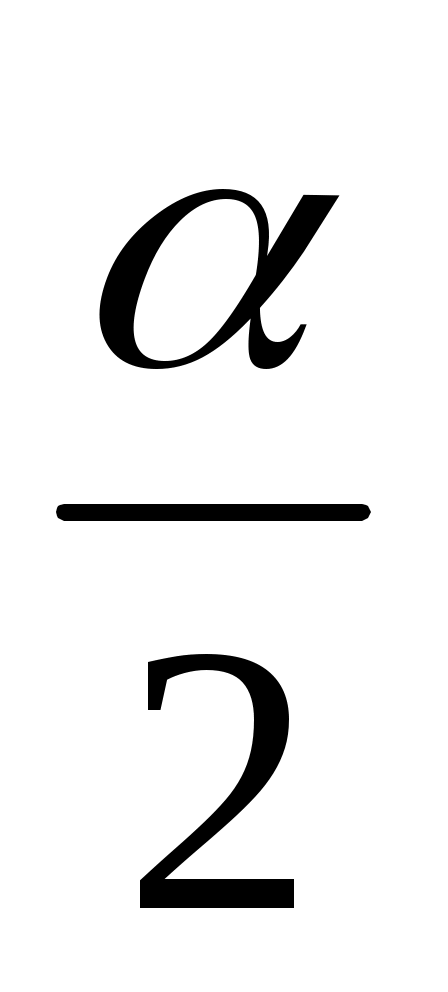 , CBE = CEB =
, CBE = CEB = 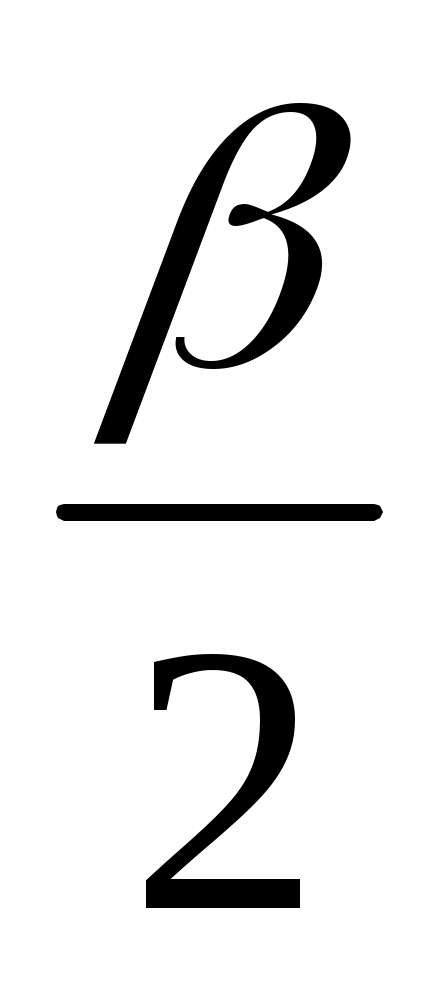 . Демек DEB үшбұрышы бір қабырғасы және оған іргелес екі бұрышы бойынша белгілі.
. Демек DEB үшбұрышы бір қабырғасы және оған іргелес екі бұрышы бойынша белгілі.
Салу: 1) DЕВ үшбұрышы (DE = p, BDE =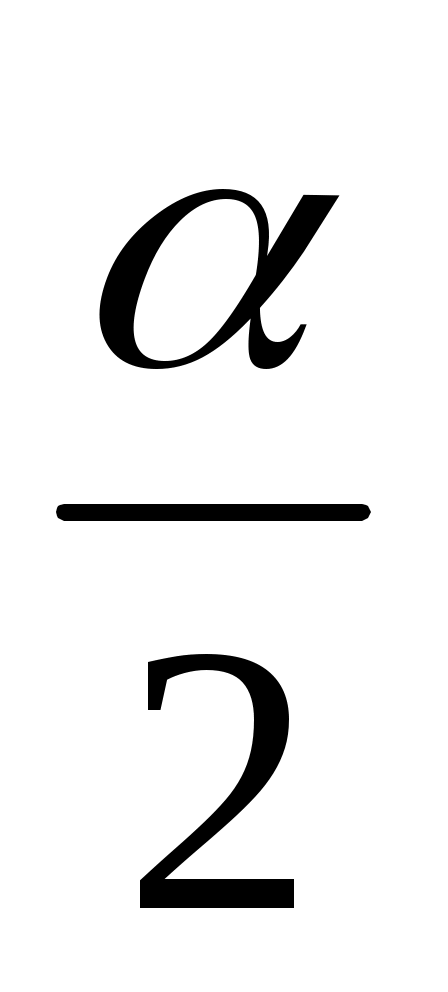 , BED =
, BED = 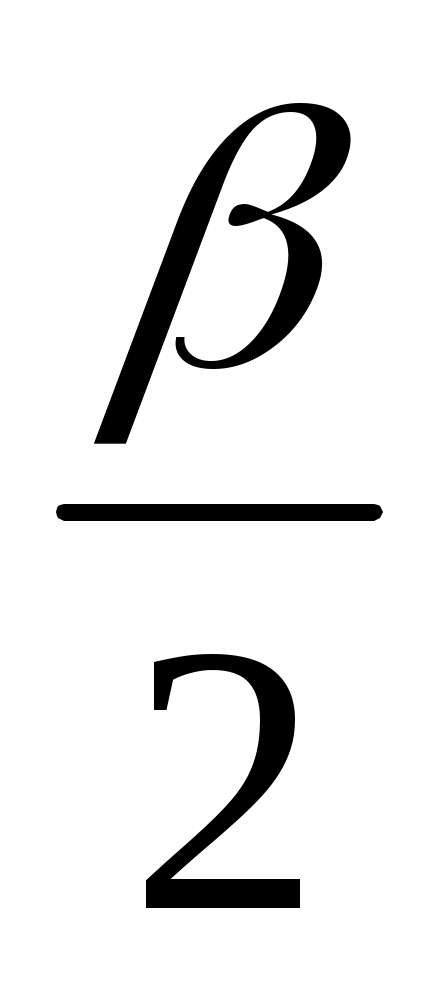 ).
).
3) DE ∩ n1 = A нүктесі
4) BЕ кесіндісінің орта перпедикуляры: n2
5) DE ∩ n2 = В нүктесі
6) АВ, СВ кесінділері
∆ АВС – ізделінді.
Дәлелдеу: n1, n2 орта перпендикулярлар болғандықтан, сәйкесінше АВ = AD, BC = CE. Ал салу бойынша DA + AC + CE = p, бұдан АВ + АС + ВС = р.
Егер n1∩ DB = K, n2 ∩ EB = P десек,
KAD = 900 -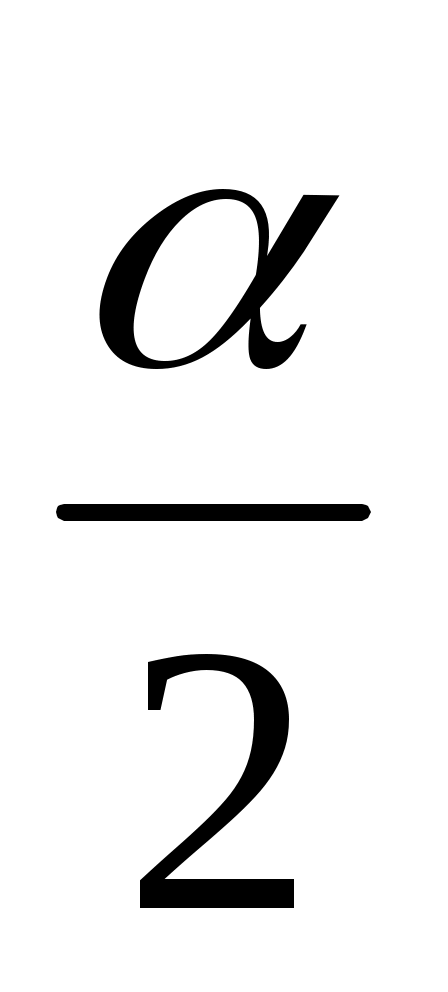 , PCE = 900 -
, PCE = 900 - 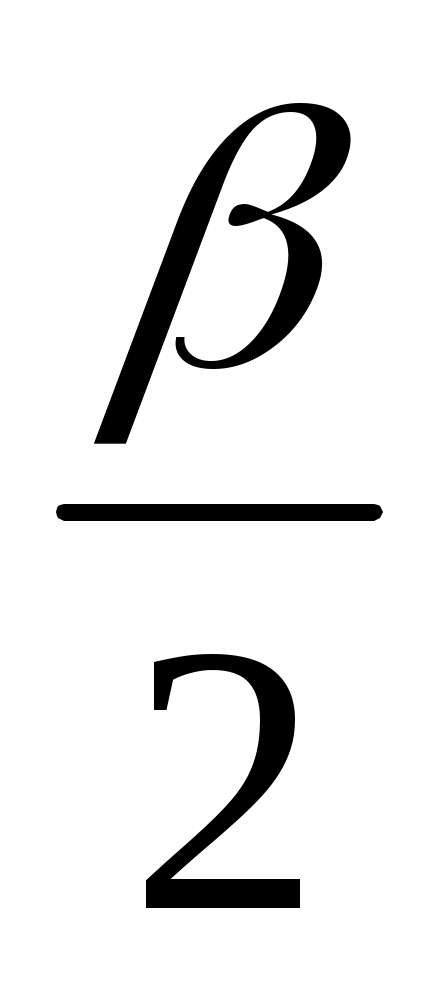 .
.
Дәл осылайша, KAВ = 900 -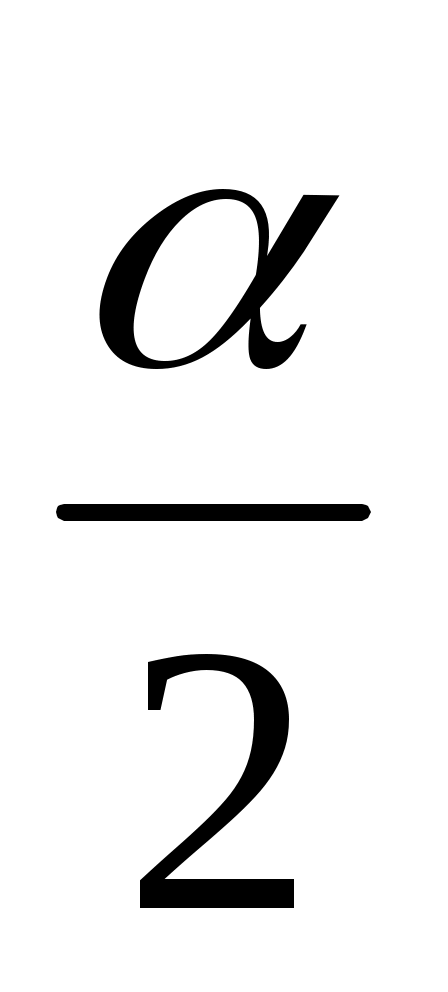 , PCВ = 900 -
, PCВ = 900 - 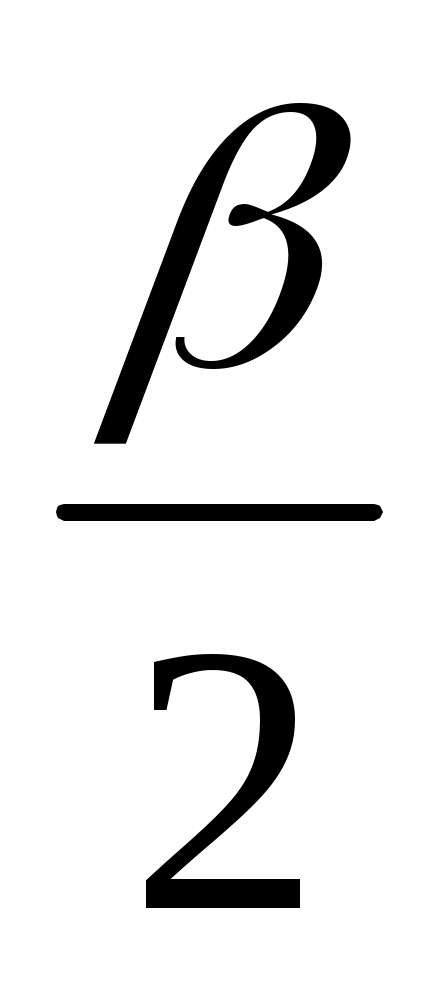
Сонда
ВАС = 1800 - ВАD = 1800 - KAВ - KAD = 1800
– 900 + - 900 +
- 900 +  =
= 
ВСA = 1800 - BCE = 1800 - PCB - PCE = 1800 – 900 + - 900 +
- 900 +  =
= 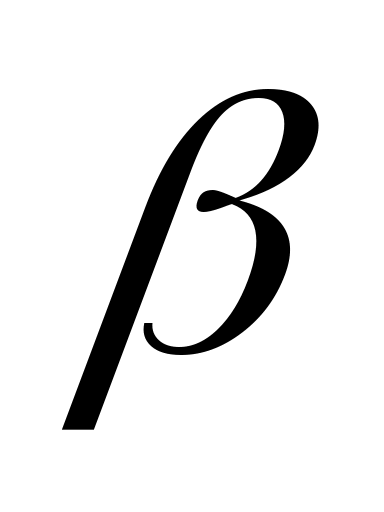
Зерттеу: + шарты орындалғанда есептің шешімі бар және ол жалғыз болады. Себебі, қарсы жорып, АВС үшбұрышы да шешім болады десек, ВАС = , ВСА = , АВ + ВС + СА = р, онда ∆АВС = ∆АВС.
Есеп 4: а, в, с түзулері, р кесіндісі берілген. с – а, в түзулерін қияды. Ұштары а, в түзулерінде болатын, с - ға параллель және р кесіндісіне тең кесінді салыңыз.
Шешуі:
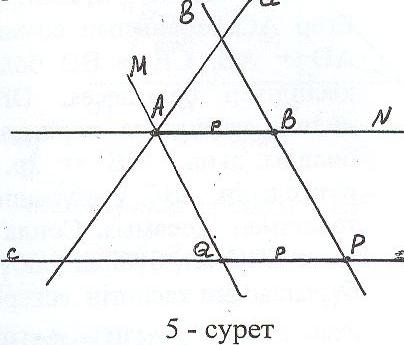
Талдау: Есеп шешілді делік, А а, В
а, В  в, АВ = р, АВ || с (5-сурет). Берілген мен ізделінді фигуралардың арасындағы байланысты анықтау үшін, кейбір қосымша нүктелер мен сызықтар жүргізу керек.
в, АВ = р, АВ || с (5-сурет). Берілген мен ізделінді фигуралардың арасындағы байланысты анықтау үшін, кейбір қосымша нүктелер мен сызықтар жүргізу керек.
Айталық с в = Р. АМ || в сәулесін жүргізсек және АМ с = Q деп белгіле-сек, АВРQ төртбұрышты параллелограмм болғандықтан PQ = AB = p.
C
алу: 1) с в = Р нүктесі
2) с түзуінен PQ = p кесіндісі (Q с )
с )
3) QМ || в түзуі
4) QM a = A нүктесі
5) AN || c түзуі
6) AN в = В нүктесі
АВ – ізделінді кесінді.
Дәлелдеу: Салу бойынша А а, В
а, В в, АВ || с. Ал АВРQ параллелограмм бол- ғандықтан, АВ = PQ = p.
в, АВ || с. Ал АВРQ параллелограмм бол- ғандықтан, АВ = PQ = p.
З
ерттеу: Есеп шарты бойынша в, с түзулері қиылысады, онда Р нүктесі әрдайым табылады. Ал екінші салу қадамындағы РQ кесіндісі екеу болады, (2.4., 3) салу). Сонда әрбір Q, Q' нүктелері үшін салу жоспары жеке орын-далады. Мынадай жағдайлар болу мүмкін:
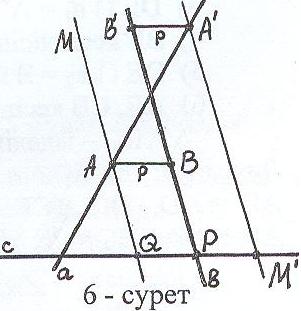
1) QM a, онда QM || в || Q'M' болғандық-
тан, Q'M' түзуі де а түзуін қияды (6-сурет).
2) QM ||a
3) QM а (беттеседі)
1) жағдай а, в түзулері қиылысқанда ғана
мүмкін. Онда 4) - 6) салу қадамдар Q, Q'
нүктелерінің әрқайсысы үшін бірмәнді
орындалады да, есептің екі шешімі болады.
2) жағдай а ||в және с түзуінің а, в түзулерінің арасындағы кесіндісі р – дан өзге болғанда ғана орындалады. Онда QMa = A нүктесі болмайды да, есептің шешімі жоқ делінеді.
3) жағдай а || в және с түзуінің а, в түзулерінің арасындағы кесіндісі р – ға тең болғанда орындалады. Онда есептің шексіз көп шешімі бар.
Есеп5: СD биссектрисасы және оның С төбесінен жүргізілген биіктікпен, медианамен арасындағы бұрыштары берілген. Осы элементтері бойынша АВС үшбұрышын салыңыз.
Шешуі:
Т
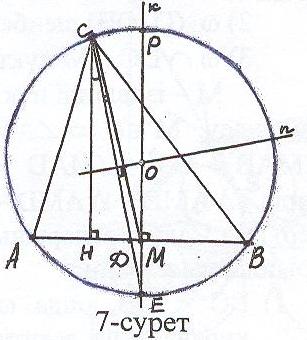
алдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш (7 – сурет). Мұндағы НСD, МСD бұрыштары және СD биссектрисасы ұшбұрыштың берілген элементтері. Онда алдымен СD гипотенузасы мен НСD бойынша НСD, содан соң СН катеті мен МСD + НСD
бойынша НСМ тікбұрышты үшбұрыштарын
тұрғызуға болады. Егер -АВС үшбұрышы-
на сырттай сызылған шеңбер десек, оның
СD биссектрисасымен қиылысу нүктесі,
яғни Е нүктесі – АВ хордасының ортасы
болады. Сондықтан ол АВ қабырғасына
тұрғызылған орта перпендикулярдың бойында
жатады, ал ол түзу М нүктесі арқылы өтеді.
Салу: 1) СD гипотенузасы мен НСD бойынша НСD тікбұрышты үшбұрышы
2) СН катеті мен НСМ = МСD + НСD бойынша НСМ тікбұрышты үшбұрышы
3) М нүктесі арқылы МК НD түзуі
4) МК СD = Е нүктесі
5) СЕ кесіндісінің орта перпендикуляры: n
6) n МК О нүктесі
7) (О, ОС) шеңбері
8) НD = А және В нүктелері
 АВС – ізделінді үшбұрыш.
АВС – ізделінді үшбұрыш.
Дәлелдеу: Салу бойынша НСD – биіктік пен биссектрисаның арасындағы бұрыш, онда
DCM = HCM - HCD = MCD + HCD - HCD = MCD.
Егер МК Р (Е – ден өзге нүкте) десек, О РЕ (РЕ – диаметр). Салу бойынша АВ РЕ, онда МА = МВ, яғни Е – АВ кесіндісінің орта перпендикулярында жатыр. Бұдан АЕ = ЕВ, яғни АСЕ ЕСВ СD – биссектриса.
РЕ (РЕ – диаметр). Салу бойынша АВ РЕ, онда МА = МВ, яғни Е – АВ кесіндісінің орта перпендикулярында жатыр. Бұдан АЕ = ЕВ, яғни АСЕ ЕСВ СD – биссектриса.
Зерттеу: Егер + 900 болса, есептің шешімі болмайды. Егер + 900
болса, есептің жалғыз шешімі бар.
Есеп 6: АВСD тіктөртбұрышы берілген. Оның СD қабырғасынан АВМ, BCM, ADM үшбұрыштары ұқсас болатындай етіп, М нүктесін табыңыз.
Шешуі:
Талдау: Есеп шешілді, яғни ізделінді М нүктесі тұрғызылды делік (8-сурет). Онда АВМ, BCM, ADM үшбұрыштарының ұқсастықтарын және С=D=900
е
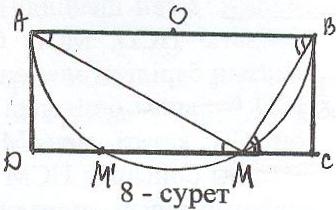
кенін ескеріп, АМВ = 900 теңдігін аламыз. Ал тікбұрышты үшбұрышқа сырттай сызылған шеңбердің қасиетін пайдалансақ М , мұндағы -диаметрі АВ болатын шеңбер.
, мұндағы -диаметрі АВ болатын шеңбер.
Салу: 1) О – АВ кесіндісінің ортасы
2) (О, ОВ) шеңбері
3) DC = М нүктесі
М – ізделінді нүкте.
Дәлелдеу: М АМВ 900, ал А В 900 екенін ескерсек, МАВ 900 - МАD АМD, дәл осылайша МВА ВМС. Онда
АМВ 900, ал А В 900 екенін ескерсек, МАВ 900 - МАD АМD, дәл осылайша МВА ВМС. Онда
 АМВ
АМВ  АМD
АМD  ВМС.
ВМС.
Зерттеу: Салу жоспарының 3) қадамына байланысты мына жағдайлар болу мүмкін:
Кейбір геометриялық салуларды тек бір құралдың көмегімен де шешуге болады. Мысалы, тек циркульдың көмегімен шешілетін салу есебін қарастырайық:
Есеп 7: Тек циркульды пайдаланып, берілген тікбұрышты үшбұрышқа іштей шеңбер сызыңыз.
Шешуі:
Талдау: Айталық АВС – катеттері а, в, гипотенузасы с болатын берілген тікбұрышты үшбұрыш, ал - оған іштей сызылған ізделінді шеңбер (9-сурет).
Ц
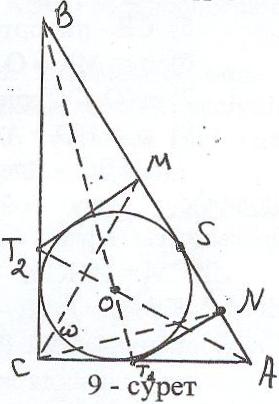
ентрі А, радиусы в болатын шеңбер жүргізіп,
Оның гипотенузамен қимасын М деп, ал центрі
В, радиусы а болатын шеңбердің гипотенузамен
қимасын N деп белгілесек, онда МN = BN – BM=
a – (c – в) = a + в – c.
Бұл сан үшбұрышқа іштей сызылған шеңбердің
диаметрі болады (есептен кейінгі ескертуде
дәлелденіп көрсетіледі).Олай болса MN кесіндісін
екіге бөлу арқылы ізделінді шеңбердің радиусын
аламыз. Ал оның центрін табу үшін оның катеттерден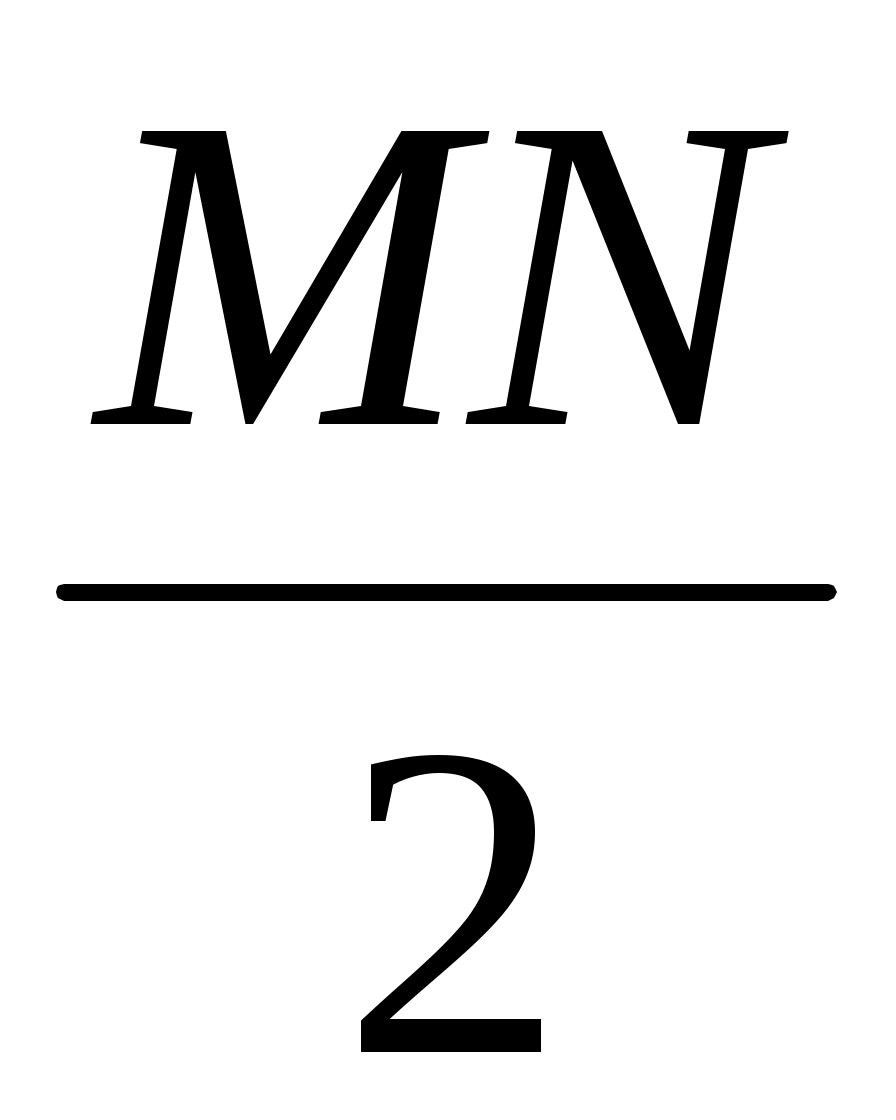 қашықтықта жататынын және (S, SN) шеңберіне тиістілігін ескереміз, мұндағы S – іштей сызылған шеңбердің гипотенузамен жанасу нүктесі.
қашықтықта жататынын және (S, SN) шеңберіне тиістілігін ескереміз, мұндағы S – іштей сызылған шеңбердің гипотенузамен жанасу нүктесі.
Салу: 1) ω1(А, в) шеңбері
2) ω2(В, а) шеңбері
3) ω1∩ АВ = М нүктесі
4) ω2∩ АВ = N нүктесі
5) ω3(N, MN) шеңбері
6) ω4(M, MN) шеңбері
7) ω3 ∩ ω4 = D нүктесі (D – АВС
үшбұрышының сыртындағы нүкте)
8) ω5(D, MN) шеңбері
9) ω5 ∩ ω3 = E нүктесі (М – нан өзге)
10) ω6(Е, MN) шеңбері
11) ω6 ∩ ω3 = F нүктесі (D – дан өзге)
12) ω7(F, MF) шеңбері
13) ω7 ∩ ω4 = L,K нүктелері
14) ω8(K, MN) шеңбері
15) ω9(L, MN) шеңбері
16) ω8 ∩ ω9 = S нүктесі (М – нан өзге)
17) ω10(S, SM) шеңбері
18) ω11(C, SN) шеңбері
19) ω11 ∩ CA = R нүктесі
20) ω12(R, CR) шеңбері
21) ω12 ∩ ω10 = O нүктесі
ω(O, MS) – ізделінді шеңбер
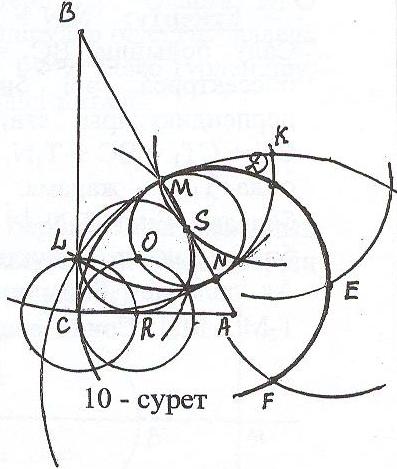
Дәлелдеу: ω10 шеңберінен SM = SO = SN (S - шеңбердің центрі, ал M, O, N оның бойындағы нүктелер (10-сурет)). Онда SM = SO = SN =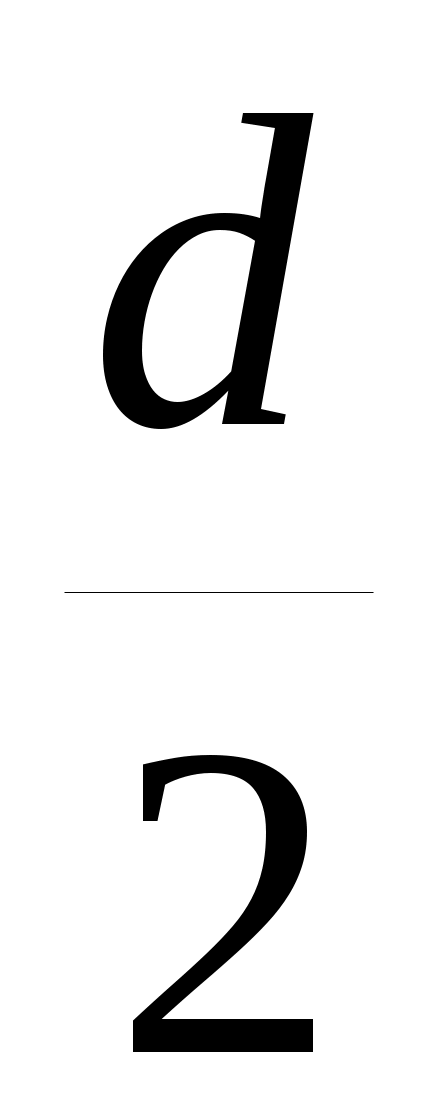 = r, яғни OS = r. Салу бойынша OR = r, онда АС – жанама АС OR және АС ВС ORBC. О нүктесінен ОТАС түзуін жүргізсек (Т ВС), ТОRС – тіктөртбұрыш. Ал OR = CR = r болғандықтан, TORC– квадрат, яғни OT=CR=r. Демек ω(O, MS) немесе ω(O, OR) – ізделінді шеңбер.
= r, яғни OS = r. Салу бойынша OR = r, онда АС – жанама АС OR және АС ВС ORBC. О нүктесінен ОТАС түзуін жүргізсек (Т ВС), ТОRС – тіктөртбұрыш. Ал OR = CR = r болғандықтан, TORC– квадрат, яғни OT=CR=r. Демек ω(O, MS) немесе ω(O, OR) – ізделінді шеңбер.
Зерттеу: а с, в с болғандықтан, салу жоспарының 1) – 15) қадамдары бірмәнді орындалады. К нүктесінен АВ қабырғасына түсірілген перпен-дикулярдың табанын Р деп белгілесек, 16) салу орындалу үшін МК РК шарты орындалу керек.
MF MN PK DS.
MD =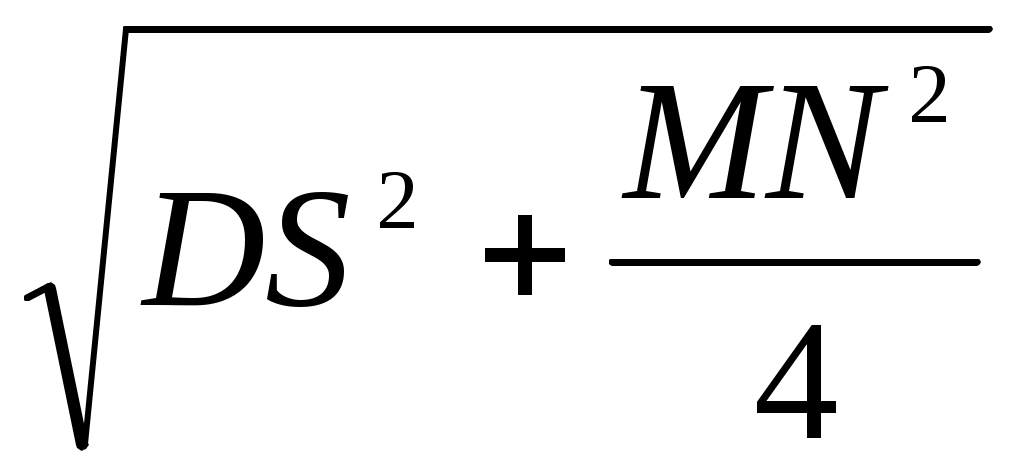 2MD =
2MD = 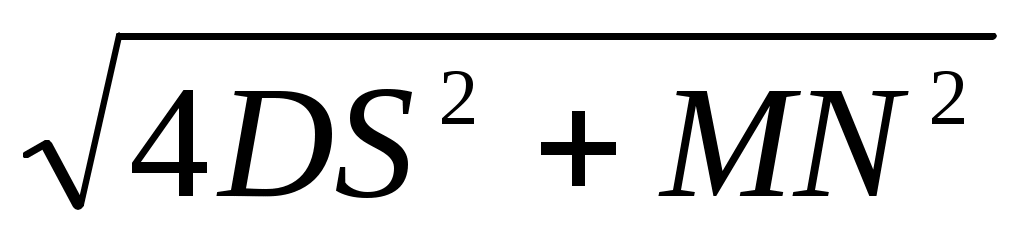 және MD = MN
және MD = MN
DS =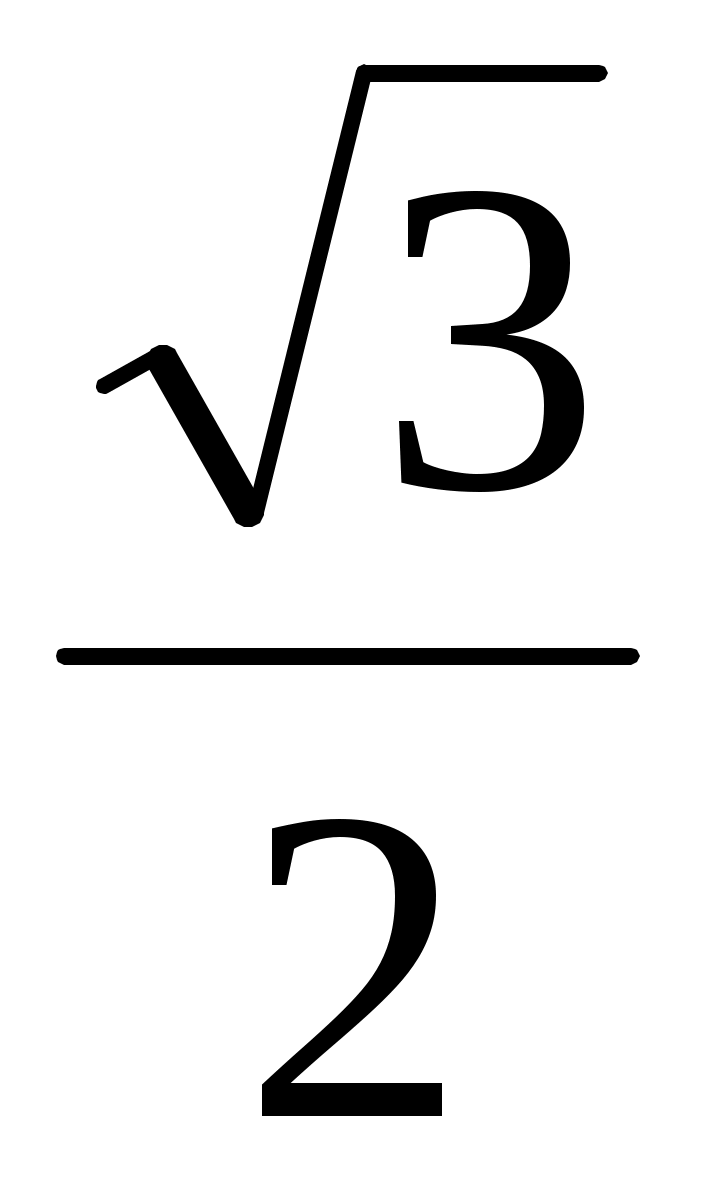 MN немесе DS =
MN немесе DS = 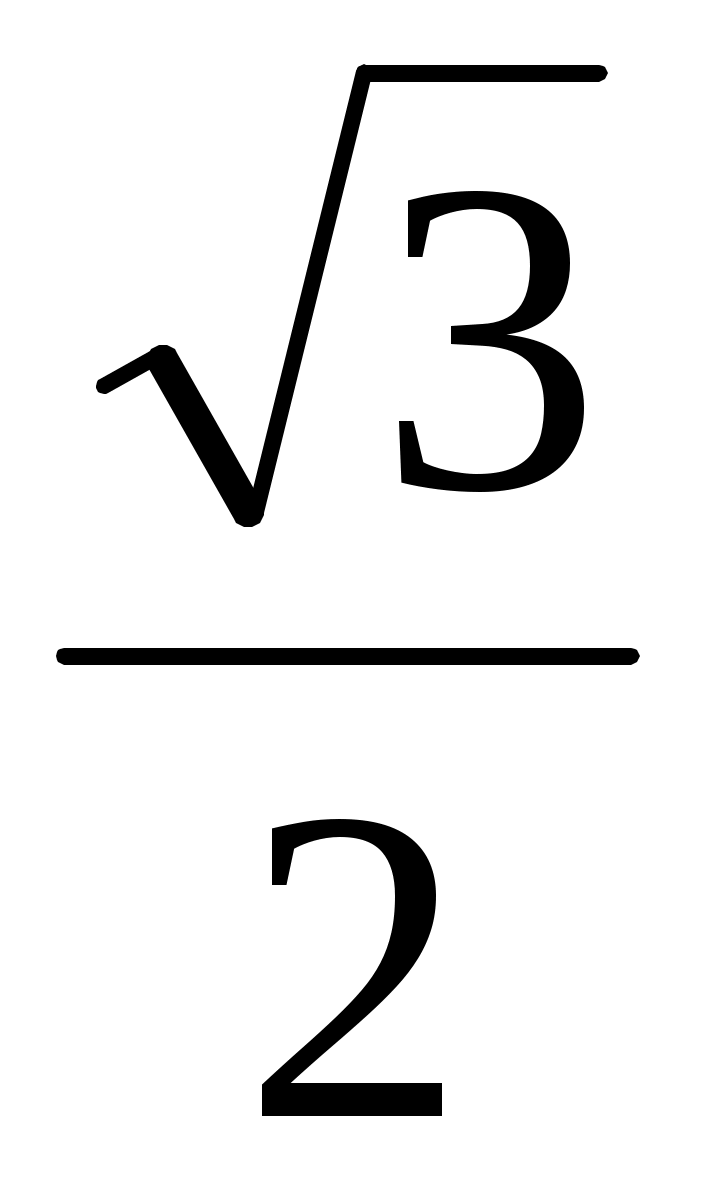 MK.
MK.
PK 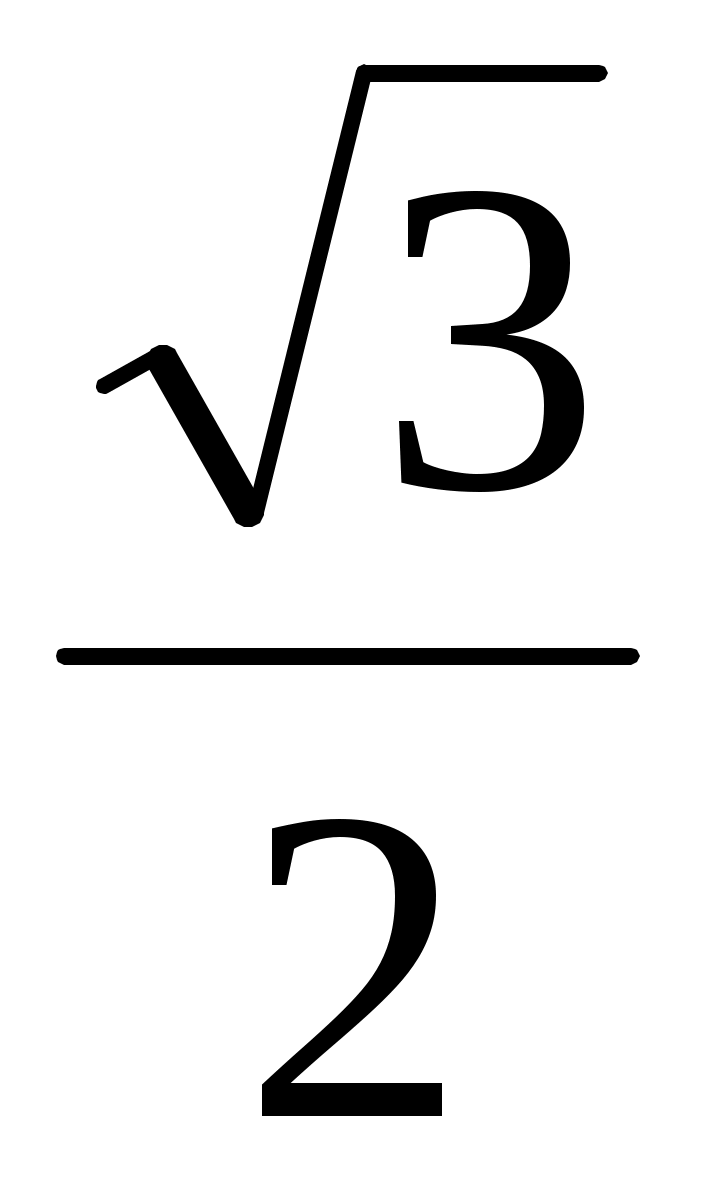 MK, онда MK
MK, онда MK 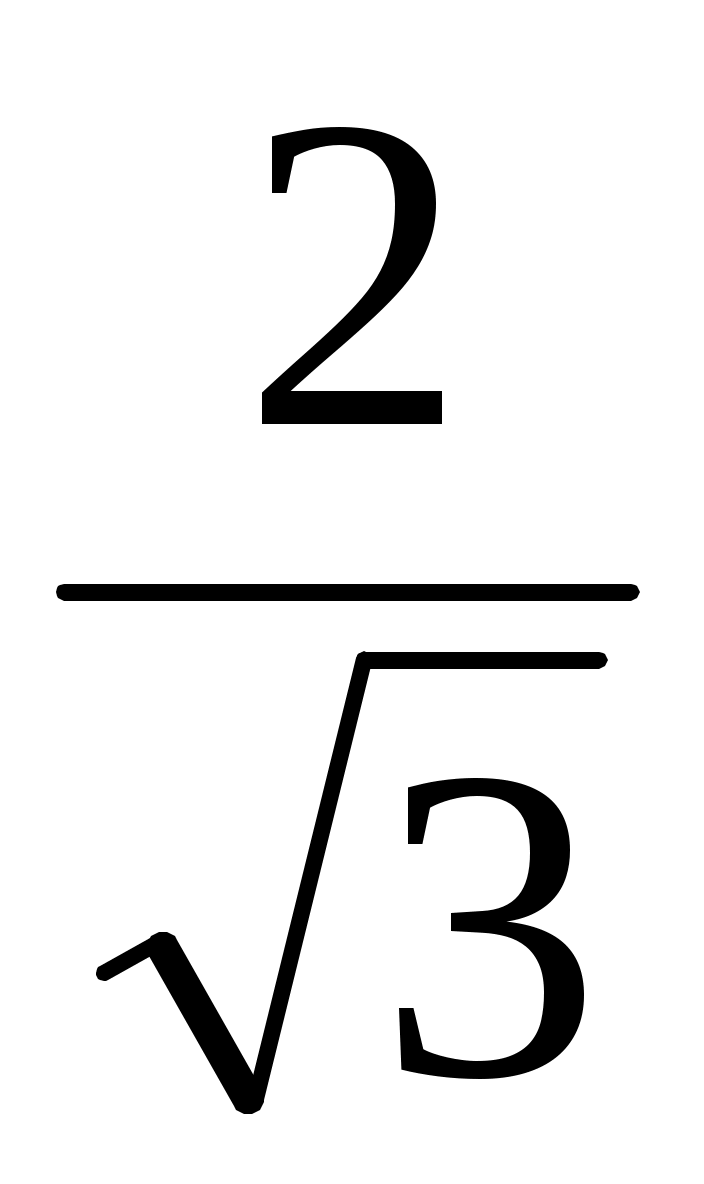
теңсіздіктері орындалғанда ғана мүмкін болады. Ал 3) – 7) салу қадамдары әрқашан орындалады. Олай болса, бір уақытта hв 2mа және hс 2mа теңсіздіктері орындалғанда есептің жалғыз шешуі бар. Басқа тәсілмен шешкенде өзге шешім шығуы мүмкін емес, себебі mа = mа, hc = hc, hв = hв ∆АВС = ∆АВС.
Есеп 3: р периметрі мен іргелес , бұрыштары бойынша үшбұрыш салу.
Шешуі:
Талдау: Айталық ВС – ізделінді үшбұрыш (4 - сурет),
А

В + ВС + СА = р
және ВАС = , ВСА = .
Егер АС табанының созындысына АD = AB,
CE = BC болатындай кесінділер белгілесек,
DE кесіндісінің ұзындығы периметрге тең
болады, яғни DE = p. D, E нүктелерін АВС
үшбұрышының В төбесімен қосамыз.
Сонда DBA және EBC тең бүйірлі үшбұрыш-
тары шығады. Үшбұрыштың сыртқы бұрышының қасиетін ескерсек, ADB = ABD =
Салу: 1) DЕВ үшбұрышы (DE = p, BDE =
-
DB кесіндісінің орта перпедикуляры: n1
3) DE ∩ n1 = A нүктесі
4) BЕ кесіндісінің орта перпедикуляры: n2
5) DE ∩ n2 = В нүктесі
6) АВ, СВ кесінділері
∆ АВС – ізделінді.
Дәлелдеу: n1, n2 орта перпендикулярлар болғандықтан, сәйкесінше АВ = AD, BC = CE. Ал салу бойынша DA + AC + CE = p, бұдан АВ + АС + ВС = р.
Егер n1∩ DB = K, n2 ∩ EB = P десек,
KAD = 900 -
Дәл осылайша, KAВ = 900 -
Сонда
ВАС = 1800 - ВАD = 1800 - KAВ - KAD = 1800
– 900 +
ВСA = 1800 - BCE = 1800 - PCB - PCE = 1800 – 900 +
Зерттеу: + шарты орындалғанда есептің шешімі бар және ол жалғыз болады. Себебі, қарсы жорып, АВС үшбұрышы да шешім болады десек, ВАС = , ВСА = , АВ + ВС + СА = р, онда ∆АВС = ∆АВС.
Есеп 4: а, в, с түзулері, р кесіндісі берілген. с – а, в түзулерін қияды. Ұштары а, в түзулерінде болатын, с - ға параллель және р кесіндісіне тең кесінді салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, А
Айталық с в = Р. АМ || в сәулесін жүргізсек және АМ с = Q деп белгіле-сек, АВРQ төртбұрышты параллелограмм болғандықтан PQ = AB = p.
C

алу: 1) с в = Р нүктесі
2) с түзуінен PQ = p кесіндісі (Q
3) QМ || в түзуі
4) QM a = A нүктесі
5) AN || c түзуі
6) AN в = В нүктесі
АВ – ізделінді кесінді.
Дәлелдеу: Салу бойынша А
З

ерттеу: Есеп шарты бойынша в, с түзулері қиылысады, онда Р нүктесі әрдайым табылады. Ал екінші салу қадамындағы РQ кесіндісі екеу болады, (2.4., 3) салу). Сонда әрбір Q, Q' нүктелері үшін салу жоспары жеке орын-далады. Мынадай жағдайлар болу мүмкін:
1) QM a, онда QM || в || Q'M' болғандық-
тан, Q'M' түзуі де а түзуін қияды (6-сурет).
2) QM ||a
3) QM а (беттеседі)
1) жағдай а, в түзулері қиылысқанда ғана
мүмкін. Онда 4) - 6) салу қадамдар Q, Q'
нүктелерінің әрқайсысы үшін бірмәнді
орындалады да, есептің екі шешімі болады.
2) жағдай а ||в және с түзуінің а, в түзулерінің арасындағы кесіндісі р – дан өзге болғанда ғана орындалады. Онда QMa = A нүктесі болмайды да, есептің шешімі жоқ делінеді.
3) жағдай а || в және с түзуінің а, в түзулерінің арасындағы кесіндісі р – ға тең болғанда орындалады. Онда есептің шексіз көп шешімі бар.
Есеп5: СD биссектрисасы және оның С төбесінен жүргізілген биіктікпен, медианамен арасындағы бұрыштары берілген. Осы элементтері бойынша АВС үшбұрышын салыңыз.
Шешуі:
Т

алдау: Есеп шешілді делік, АВС – ізделінді үшбұрыш (7 – сурет). Мұндағы НСD, МСD бұрыштары және СD биссектрисасы ұшбұрыштың берілген элементтері. Онда алдымен СD гипотенузасы мен НСD бойынша НСD, содан соң СН катеті мен МСD + НСD
бойынша НСМ тікбұрышты үшбұрыштарын
тұрғызуға болады. Егер -АВС үшбұрышы-
на сырттай сызылған шеңбер десек, оның
СD биссектрисасымен қиылысу нүктесі,
яғни Е нүктесі – АВ хордасының ортасы
болады. Сондықтан ол АВ қабырғасына
тұрғызылған орта перпендикулярдың бойында
жатады, ал ол түзу М нүктесі арқылы өтеді.
Салу: 1) СD гипотенузасы мен НСD бойынша НСD тікбұрышты үшбұрышы
2) СН катеті мен НСМ = МСD + НСD бойынша НСМ тікбұрышты үшбұрышы
3) М нүктесі арқылы МК НD түзуі
4) МК СD = Е нүктесі
5) СЕ кесіндісінің орта перпендикуляры: n
6) n МК О нүктесі
7) (О, ОС) шеңбері
8) НD = А және В нүктелері
Дәлелдеу: Салу бойынша НСD – биіктік пен биссектрисаның арасындағы бұрыш, онда
DCM = HCM - HCD = MCD + HCD - HCD = MCD.
Егер МК Р (Е – ден өзге нүкте) десек, О
Зерттеу: Егер + 900 болса, есептің шешімі болмайды. Егер + 900
болса, есептің жалғыз шешімі бар.
Есеп 6: АВСD тіктөртбұрышы берілген. Оның СD қабырғасынан АВМ, BCM, ADM үшбұрыштары ұқсас болатындай етіп, М нүктесін табыңыз.
Шешуі:
Талдау: Есеп шешілді, яғни ізделінді М нүктесі тұрғызылды делік (8-сурет). Онда АВМ, BCM, ADM үшбұрыштарының ұқсастықтарын және С=D=900
е

кенін ескеріп, АМВ = 900 теңдігін аламыз. Ал тікбұрышты үшбұрышқа сырттай сызылған шеңбердің қасиетін пайдалансақ М
Салу: 1) О – АВ кесіндісінің ортасы
2) (О, ОВ) шеңбері
3) DC = М нүктесі
М – ізделінді нүкте.
Дәлелдеу: М
Зерттеу: Салу жоспарының 3) қадамына байланысты мына жағдайлар болу мүмкін:
-
ВС ОВ, онда DC қимасы М және М нүктелерінен құралады да, есептің екі шешімі болады. -
ВС = ОВ, онда DC = М – жалғыз нүкте, олай болса, есептің бір ғана шешімі бар. -
ВС ОВ, онда DC = , яғни есептің шешімі жоқ.
Кейбір геометриялық салуларды тек бір құралдың көмегімен де шешуге болады. Мысалы, тек циркульдың көмегімен шешілетін салу есебін қарастырайық:
Есеп 7: Тек циркульды пайдаланып, берілген тікбұрышты үшбұрышқа іштей шеңбер сызыңыз.
Шешуі:
Талдау: Айталық АВС – катеттері а, в, гипотенузасы с болатын берілген тікбұрышты үшбұрыш, ал - оған іштей сызылған ізделінді шеңбер (9-сурет).
Ц

ентрі А, радиусы в болатын шеңбер жүргізіп,
Оның гипотенузамен қимасын М деп, ал центрі
В, радиусы а болатын шеңбердің гипотенузамен
қимасын N деп белгілесек, онда МN = BN – BM=
a – (c – в) = a + в – c.
Бұл сан үшбұрышқа іштей сызылған шеңбердің
диаметрі болады (есептен кейінгі ескертуде
дәлелденіп көрсетіледі).Олай болса MN кесіндісін
екіге бөлу арқылы ізделінді шеңбердің радиусын
аламыз. Ал оның центрін табу үшін оның катеттерден
Салу: 1) ω1(А, в) шеңбері
2) ω2(В, а) шеңбері
3) ω1∩ АВ = М нүктесі
4) ω2∩ АВ = N нүктесі
5) ω3(N, MN) шеңбері
6) ω4(M, MN) шеңбері

7) ω3 ∩ ω4 = D нүктесі (D – АВС
үшбұрышының сыртындағы нүкте)
8) ω5(D, MN) шеңбері
9) ω5 ∩ ω3 = E нүктесі (М – нан өзге)
10) ω6(Е, MN) шеңбері
11) ω6 ∩ ω3 = F нүктесі (D – дан өзге)
12) ω7(F, MF) шеңбері
13) ω7 ∩ ω4 = L,K нүктелері
14) ω8(K, MN) шеңбері
15) ω9(L, MN) шеңбері
16) ω8 ∩ ω9 = S нүктесі (М – нан өзге)
17) ω10(S, SM) шеңбері
18) ω11(C, SN) шеңбері
19) ω11 ∩ CA = R нүктесі
20) ω12(R, CR) шеңбері
21) ω12 ∩ ω10 = O нүктесі
ω(O, MS) – ізделінді шеңбер
Дәлелдеу: ω10 шеңберінен SM = SO = SN (S - шеңбердің центрі, ал M, O, N оның бойындағы нүктелер (10-сурет)). Онда SM = SO = SN =
Зерттеу: а с, в с болғандықтан, салу жоспарының 1) – 15) қадамдары бірмәнді орындалады. К нүктесінен АВ қабырғасына түсірілген перпен-дикулярдың табанын Р деп белгілесек, 16) салу орындалу үшін МК РК шарты орындалу керек.
MF MN PK DS.
MD =
DS =
PK