Файл: Мазмны Кiрiспе 1 тарау. Геометриялы салулар теориясыны кейбiр мселелерi 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 226
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§2. Түрлендірулер әдісі
Айталық жазықтықтағы Ф фигурасының әрбір М нүктесіне осы жазықтықтың қандай да бір анықталған М' нүктесін сәйкестендіретіндей ереже орнатылған болсын. Онда жазықтықта Ф фигурасының түрлендіруі берілген делінеді. М' - М нүктесінің образы, ал М - М' нүктесінің прообразы деп аталады. Берілген Ф фигурасының нүктелеріне сәйкестендірілген нүктелер жиыны Ф' фигурасын құрайды және ол фигураны Ф-ң образы деп атайды.
Түрлендіруді геометриялық салулар теориясында қолдану геометриялық турлендірулер әдісі деп аталады. Түрлендірулер әдісінің негізгі мақсаты – берілген немесе ізделінді фигураларды түрлендіре отырып, есепті оңай шешілетіндей қарапайым түрге келтіру. Көптеген салу есептерін шешуде жазықтықты геометриялық түрлендіру нәтижелі қолданылады. Енді солардың түрлеріне тоқталып өтейік.
2.1. Параллель көшіру әдісі
Параллель көшіру, көрнекі түрде, нүктелері бір бағытта, бірдей арақа-шықтыққа көшірілетін түрлендіру деп түсіндіріледі.
Жазықтықта декарттық координаталар системасын енгіземіз. Кез - келген (х, у) нүктесі жазықтықтың (х+а, у+в) нүктесіне көшетіндей Ғ фигурасын түрлендіру параллель көшіру деп аталады, мұндағы а,в сандары барлық (х,у) нуктелері үшін бірдей. Параллель көшіру х'=х+а, у'=у+в формулаларымен беріледі. Бұл формулалар параллель көшірудегі (х,у) нүктесі көшетін нүктенің х', у' координаталарын көрсетеді (21-сурет).
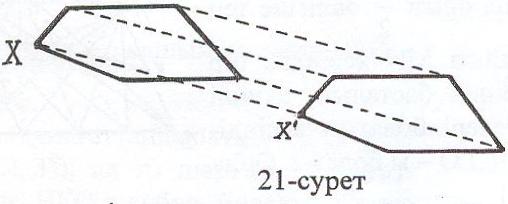
Параллель көшіру – қозғалыс.
Параллель көшіруде нүктелер параллель (немесе беттесетін) түзулер бойымен бірдей қашықтыққа ауысады. Параллель көшіруде түзу өзіне параллель түзуге немесе өз - өзіне көшеді.
Параллель көшіруді геометриялық салуларда қолдану параллель көшіру әдісі деп аталады. Осы әдіс бойынша есепті шешуге берілген немесе ізделінді фигураларды не олардың элементтерін параллель көшіруден пайда болған фигуралар қарастырылады. Бұл есепке талдау жасауды барынша жеңілдетеді.
Параллель көшіру әдісі фигураның «шашыраңқы» бөліктерін біріктіруде, көпбұрыштарды (әсіресе, төртбұрыштарды) салуда жиі қолданылады. Мұнда, әдетте, бір немесе бірнеше кесінділердің параллель көшірудегі образдарын қарастыру арқылы салуды жеңілдететін қосымша фигуралар (мысалы, үшбұрыш) қарастырылады.
Мысал: Берілген төрт қабырғасы бойынша трапеция салыңыз.
Шешуі:
Т
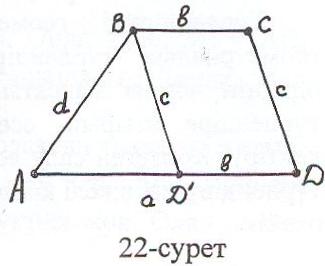
алдау. Есеп шешілді делік, яғни ізделінді АВСД трапециясы тұрғызылған. АD = а – үлкен табан, ВС = в – кіші табан, ал АВ = d және СD = c – бүйір қабырғалар.(22-сурет)
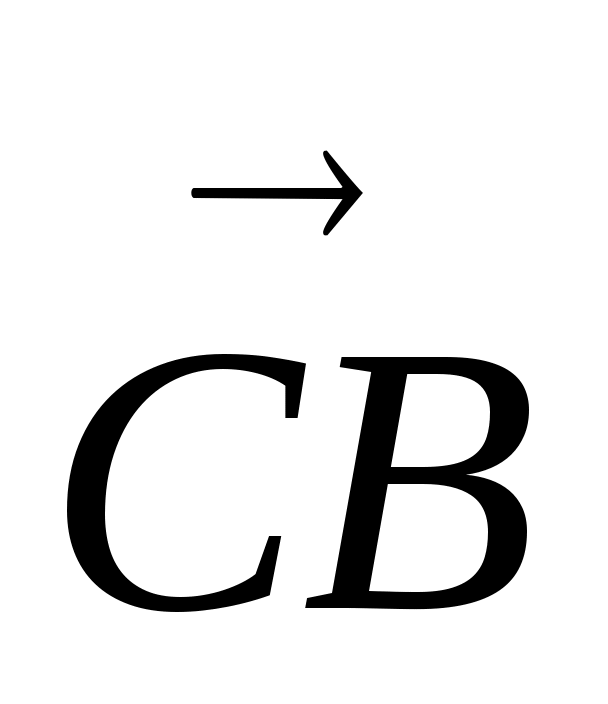 векторына қатысты параллель көшіру
векторына қатысты параллель көшіру
қарастырайық. Сонда СD қабырғасы ВD'
(D' АD) қабырғасына көшеді. АВD' үшбұ-
АD) қабырғасына көшеді. АВD' үшбұ-
рышын берілген үш қабырғасы бойынша
салу оңай. Онда ізделінді трапецияны салу
үшін ВD' кесіндісін  векторы бағытымен, ұзындығы в–ға тең болатындай қашықтыққа параллель көшіреміз.
векторы бағытымен, ұзындығы в–ға тең болатындай қашықтыққа параллель көшіреміз.
Салу. 1) АВ = d, ВD' = с, АD' = а - в қабырғалары бойынша АВD' үшбұрышы
2) АD' түзуі
3) АD = а кесіндісі, А-D'-D және D AD'
4) ТД'Д : ВD'→СD кесіндісі
5) ВС кесіндісі
АВСD - ізделінді трапеция
Дәлелдеу. Салу бойынша АD = а, АВ = d, алпараллель көшірудің қасиеті бойынша СD = с, ВС AD. Сонда ВС = DD' = АD - АD' = а - (а – в) = в.
Зерттеу. Егер СD – АВ < АD – ВС < СD + АВ қатынасы орындалса, есептің бір ғана шешуі бар. Қалған жағдайларда есептің шешімі жоқ.
2.2. Осьтік симметрия әдісі

Айталық р - берілген түзу. Кез-келген Х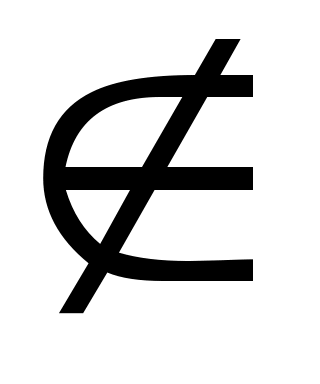 р нүктесінен р түзуіне АХ перпендикулярын (А
р нүктесінен р түзуіне АХ перпендикулярын (А р) түсіреміз (23-сурет). Осы перпендикулярдың созындысына А нүктесінің екінші жағынан
р) түсіреміз (23-сурет). Осы перпендикулярдың созындысына А нүктесінің екінші жағынан
АХ - қа тең АХ' кесіндісін салсақ, Х' р
түзуіне қарағанда Х нүктесіне симметриялы
нүкте болады. Егер Х р болса, онда оған р
р болса, онда оған р
түзуіне қатысты симметриялы нүкте өзі болады.
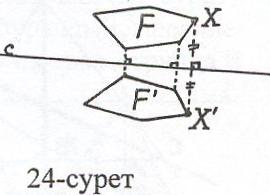
Әрбір Х нүктесі с түзуіне қарағанда симметриялы Х' нүктесіне көшетіндей Ғ фигурасын Ғ' фигурасына түрлендіру осьтік симметрия деп аталады. Мұндағы, Ғ, Ғ' – с түзуіне қатысты симметриялы фигуралар (24-сурет). Егер осьтік симметрияда Ғ фигурасы өз-өзіне
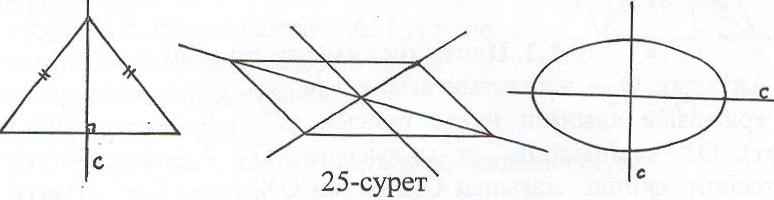
көшсе, онда оны түзуге қатысты симмет-
риялы фигура деп атайды, ал с – оның
симметрия осі болады.(25-сурет)
Осьтік симметрия – қозғалыс.
Салу есептерін шешу барысында осьтік симметрияның қасиеттері қолданылуы мүмкін. Мұндай жағдайда анализде берілген фигураға, не оның элементіне қандай да бір түзуге қатысты симметриялы фигура салып аламыз. Нәтижесінде оңай шешілетін немесе қарапайым түрдегі «жаңа» есеп алынады.
Осьтік симметрияны қолдану сызықтарды түзумен алмастыруға, берілген фигураның «шашыраңқы» элементтерін жақынтуға мүмкіндік береді.
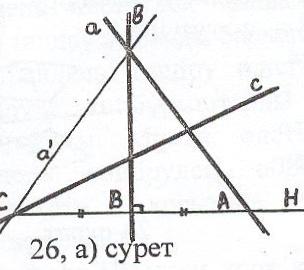
Мысал: Қос-қостан қиылысатын a, в, с үш түзуі берілген. в түзуіне перпендикуляр болып, ортасы в түзуінде, ал ұштары а, с түзулерінде жататын кесінді салыңыз.
Шешуі:
Талдау. Есеп шешілді делік, АС – ізделінді кесінді (26, а) сурет). Онда А а, С
а, С с, В
с, В в және АВ=ВС, АСв. Бұдан в түзуіне қарағандағы симметрияда А нүктесі С нүктесіне немесе С нүктесі А нүктесіне көшеді.
в және АВ=ВС, АСв. Бұдан в түзуіне қарағандағы симметрияда А нүктесі С нүктесіне немесе С нүктесі А нүктесіне көшеді.
Салу. 1) Sв: а → а' түзуі
-
С = а'  с нүктесі
с нүктесі
-
СН в түзуі
-
А = СН  а нүктесі
а нүктесі
АС – ізделінді кесінді.
Дәлелдеу. Салуымыз бойынша АС в. Осьтік симметрияның қасиеті бойынша, в –  (а, а') бұрышының биссектрисасы болады. Ал бұдан АС в екенін ескерсек, АВ = ВС.
(а, а') бұрышының биссектрисасы болады. Ал бұдан АС в екенін ескерсек, АВ = ВС.
Зерттеу. Мынандай жағдайлар болу мүмкін:
1) с және а' түзулері қиылысады, онда есептің бір ғана шешімі бар (26,а) сурет)
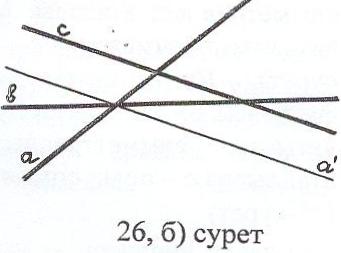
2) с және а' түзулері параллель, онда есептің шешімі болмайды (26, б) сурет)
2.3. Центрлік симметрия әдісі
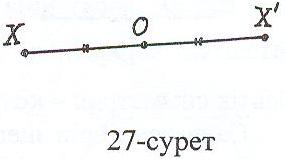
Айталық О – жазықтықтағы нүкте, ал Х – еркімізше алынған нүкте болсын (27-сурет). ОХ кесіндісінің созындысына О нүктесінің екінші жағынан ОХ -
қ
а тең ОХ' кесіндісін өлшеп салайық. Сонда
Х' нүктесі О нүктесіне қарағанда Х нүктесіне
симметриялы деп аталады. О нүктесіне сим -
метриялы нүкте оның өзі болады.
Ғ фигурасын оның әрбір Х нүктесі берілген О нүктесіне қарағанда симметриялы Х' нүктесіне көшетін етіп, Ғ' фигурасына түрлендіру О нүктесіне қатысты симметрия арқылы түрлендіру деп аталады (28-сурет).
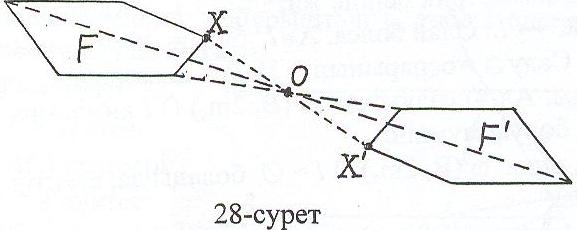
Сонда Ғ және Ғ ' фигуралары О нүктесіне қатысты симметриялы фигуралар болады.
Егер О нүктесіне қарағанда центрлік симметрияда Ғ фигурасын өз-өзіне көшіретін болса, онда Ғ фигурасының симметрия центрі бар деп аталады, О нүктесі симметрия центрі болады. Мысалы, параллелограмның симметрия центрі оның диагональдарының қиылысу нүктесі болады.
Салу есептерін шешуде центрлік симметрияны қолдану центрлік симметрия әдісі деп аталады. Бұл әдіс бойынша берілген немесе ізделінді фигуралардың, не олардың кейбір элементтерінің қандай да бір нүктеге қатысты симметриялары қарастырылады. Центрлік симметрия әдісін, әдетте, фигураның немесе оның бөлігінің симметрия центрі болған жағдайда қолданған ыңғайлы.
Мысал: Бір қабырғасы, оған жүргізілген биіктігі және басқа екі қабырғаның біріне жүргізілген медианасы бойынша үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, яғни АВС - ізделінді үшбұрыш (29-сурет). Онда
В
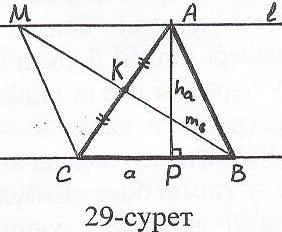
К = mв (АК = КС), АР = ha, ВС = а. АВС
үшбұрышын параллелограмға толықтырсақ,
К нүктесіне қатысты центрлік симметрияда
В нүктесі М нүктесіне көшеді. Олай болса,
МВ = 2mв. Сонымен М нүктесі екі геометрия-
риялық орынға тиісті:
Ғ1: ω(В, 2mв) шеңберіне
Ғ2: ВС түзуінен hа қашықтықтағы АМ түзуіне
Сонда осы айтылғандарды ескере отырып, салу жоспарын былайша құра аламыз:
Салу: 1) ВС = а кесіндісі
2) ВС түзуінен hақашықтықтағы параллель түзу: l
3) ω (В, 2mв) шеңбері
4) ω (В, 2mв) ∩ l = М нүктесі
5) МВ кесіндісі
6) К – МВ кесіндісінің ортасы
7) Sк : С → А нүктесі
8) АВ түзуі
АВС – ізделінді үшбұрыш
Дәлелдеу: Салуымыз бойынша ВС = а, МВ = 2mв. Онда центрлік симмет-рияның қасиетінен ВК = mв. Бұдан ВС l болғандықтан, К осы түзулердің симметрия осінде жатады (3.1.2. Қарапайым ГО, 3)), яғни Sк : ВС → l. Олай болса, А  l, бұдан АР = hа шығады.
l, бұдан АР = hа шығады.
Зерттеу: Салу жоспарының 1) - 3) қадамдары әрдайым бірмәнді орындалады. Ал 4) салуында ω (В, 2mв) ∩ l қимасына байланысты мына жағдайлар болуы мүмкін:
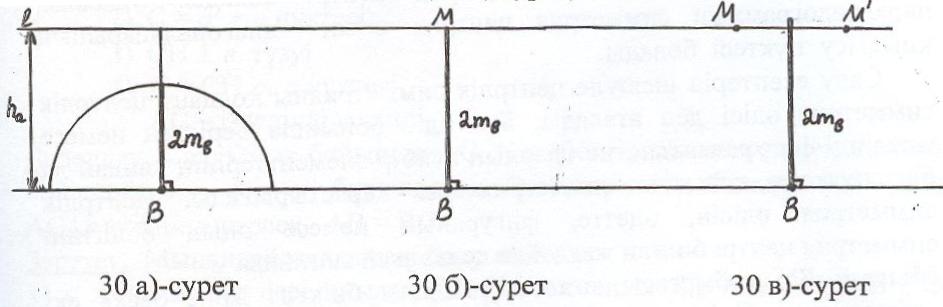
а) 2mв < hа, онда ω(В, 2mв) ∩ l= болады да, есептің шешімі жоқ (30 а) сурет);
б) 2mв = hа, онда ω(В, 2mв) ∩ l қимасы бір нүктеден құралады да, есептің жалғыз шешімі болады (30 б)-сурет);
в) 2mв hа, онда ω(В, 2mв) ∩ l қимасы М және М' нүктелерінің қосынан құралады. Бұл жағдайда әр нүкте үшін салу жоспары бөлек орындалады да, есептің екі шешімі бар (30 в)-сурет).
2.4. Бұру әдісі
Берілген нүктені айналдыра жазықтықты бұру деп, осы нүктеден шыққан әрбір сәуле бір бағытта, бірдей бұрышқа бұрылатын қозғалысты айтады.
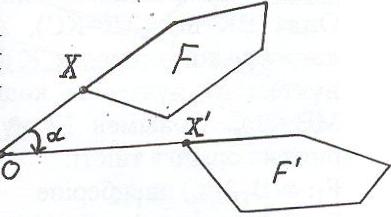
Егер О нүктесін айналдыра бұруда Х нүктесі Х' нүктесіне көшсе (31-сурет), онда Х нүктесі қандай болмасын ОХ және ОХ' сәулелері бірдей бұрыш құрайды. Бұл бұрыш бұру бұрышы деп аталды.
Бұрудың қозғалыс болатыны жеңіл дәлелденеді.
Кейбір салу есептерін шешуде бұруды пайда-
лану тиімді болады. Бұл әдістің мәнісі мынада:
талдауды жеңілдету үшін немесе есептің шешімін
бірден табу үшін фигураның кейбір элементтерін
берілген центрден берілген бұрышқа бұрады. 31 – сурет
Мысал: Параллель екі түзу және олармен шектелген жолақтан А нүктесі берілген. Екі төбесі берілген түзулерде, бір төбесі берілген нүкте болатын тең қабырғалы үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, яғни в║с, А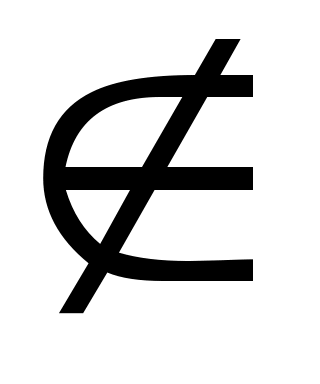 в, А
в, А 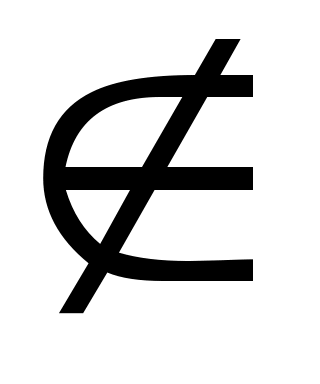 с, В
с, В в, С
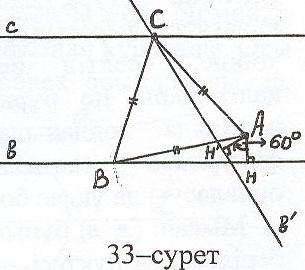
в, С с, АВ = ВС = АС (32-сурет). АВС үшбұрышы дұрыс болғандықтан, А = 600 (В = С = 600). Олай болса, В төбесін 600-қа сағат тілімен бағыттас бұрсақ, ізделінді үшбұ-рыштың С төбесі шығады. Ендеше салу жоспары төмендегідей:
с, АВ = ВС = АС (32-сурет). АВС үшбұрышы дұрыс болғандықтан, А = 600 (В = С = 600). Олай болса, В төбесін 600-қа сағат тілімен бағыттас бұрсақ, ізделінді үшбұ-рыштың С төбесі шығады. Ендеше салу жоспары төмендегідей:
С
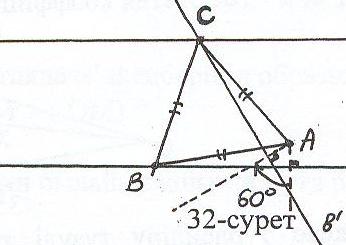
алу: 1) R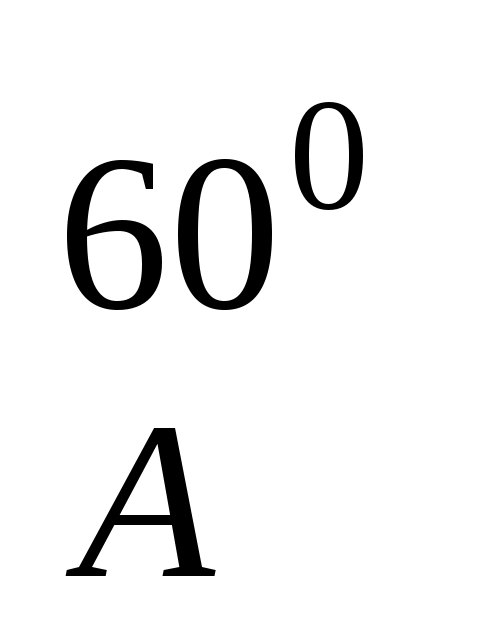 : в→в' түзуі
: в→в' түзуі
2) С = в' с нүктесі с
3) (А, АС) шеңбері
4) В = в нүктесі в
5) АВ, ВС, СА кесінділері
АВС – ізделінді үшбұрыш.
Дәлелдеу: R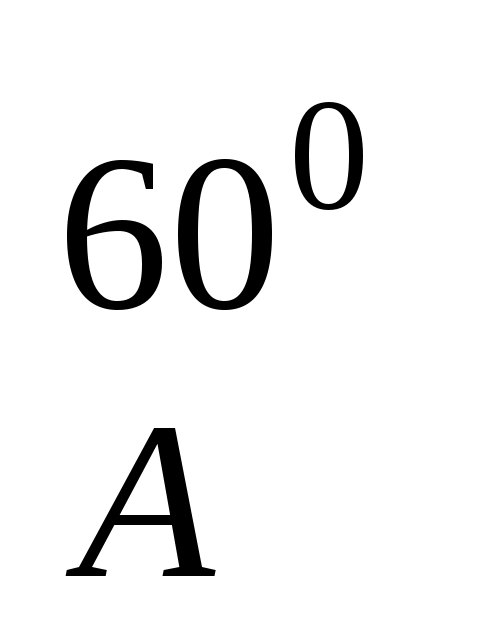 : в→в' болғандықтан АС, АВ кесінділерінің арасындағы бұрыш 600-ты құрайды, яғни САВ = 600. АС = АВ (радиустар), бұдан АСВ = АВС. Онда АСВ =
: в→в' болғандықтан АС, АВ кесінділерінің арасындағы бұрыш 600-ты құрайды, яғни САВ = 600. АС = АВ (радиустар), бұдан АСВ = АВС. Онда АСВ = 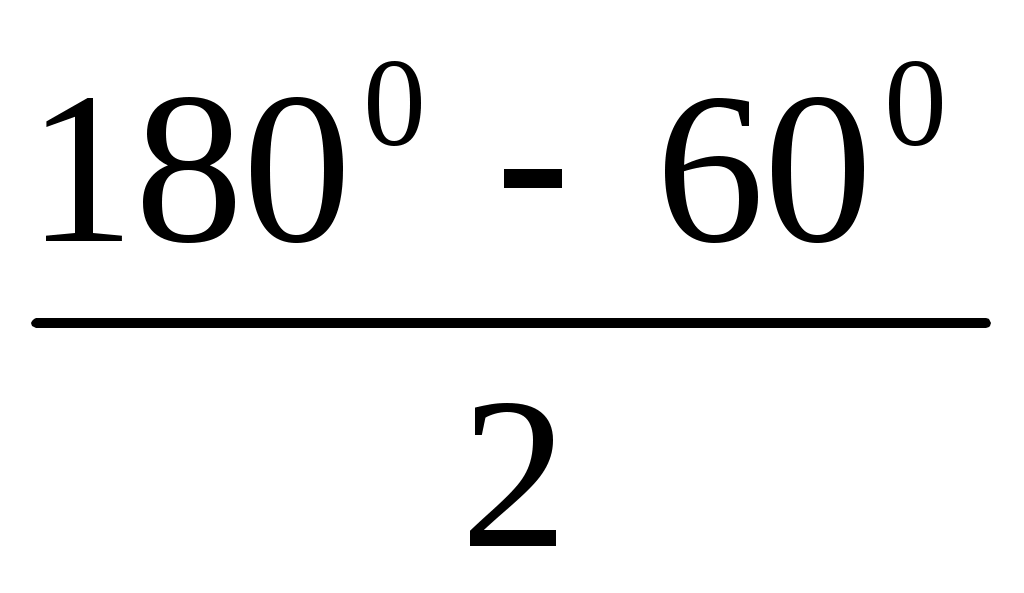 = 600. Олай болса, АВС – тең қабырғалы үшбұрыш.
= 600. Олай болса, АВС – тең қабырғалы үшбұрыш.
Зерттеу: Салу жоспарының 1) – 3) қадамдары орындалады, ал 4)-ші қадамға байланысты мына жағдайларды қарастырайық:
а) в, яғни АС АН. Онда АН = АН болғандықтан АС АН. Бірақ бұлай болу мүмкін емес, себебі АСН үшбұрышында АС – гипотенуза. Сонда шеңбері мен в түзуі міндетті түрде қиылысады (33-сурет).
б
) в қимасы бір нүкте – В нүктесі, онда АС=АН.
Бұдан АС=АН, бірақ тікбұрышты үшбұрышта гипо-
тенуза мен катет тең болуы мүмкін емес.
в) в қимасы В және В нүктелерінен құралған.
Осы екі нүктенің біреуі үшін ғана салу жоспары
орындалады, себебі САВ ≠ САВ. Сонымен
есептің жалғыз шешімі болады.
2.5. Ұқсас түрлендіру әдісі
Егер Ғ фигурасын Ғ фигурасына түрлендіргенде нүктелердің арақашық-тығы бірдей сан есе өзгеретін (артады немесе кемиді) болса, онда мұндай түрлендіру ұқсас түрлендіру деп аталады.
Е
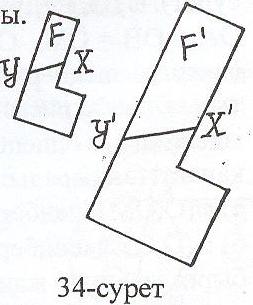
гер Ғ фигурасының еркімізше алынған Х, У нүктелері ұқсас түрлендіргенде Ғ фигурасының Х, У нүктелеріне көшсе, онда ХУ = к∙ХУ болады (34-сурет), мұндағы к – Х, У нүктелері үшін бірдей сан.
к саны ұқсастық коэффиценті деп аталады.
к=1 болғанда ұқсас түрлендіру – қозғалыс.
Айталық Ғ берілген фигура және О – бел-
гіленген нүкте. Ғ фигурасының кез-келген Х
нүктесі арқылы ОХ сәулесін жүргізіп, оған
к
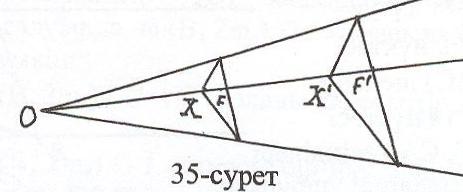
∙ОХ оң санына тең ОХ кесіндісін белгілейміз. Осы «заңдылық» бойынша әрбір Х нүктесі Ғ фигурасының Х нүктесіне көшетін Ғ фигурасын Ғ–қа түрлендіруді О центріне қатысты гомотетия деп атайды, ал к – гомотетия коэффиценті болады (35 – сурет).
Ұқсас түрлендіру түзуді түзуге, жарты түзуді жарты түзуге, кесіндіні кесіндіге көшіреді. Ұқсас түрлендіруде жарты түзулердің арасындағы бұрыш сақталады.
Ұқсас түрлендіру арқылы бір – біріне көшірілетін фигуралар ұқсас деп аталады. Ұқсас көпбұрыштардың сәйкес бұрыштары тең, ал сәйкес кесінділері пропорционал. Мысалы, ΔАВС
ΔА′В′С′ болса, онда А = A, B = B, C = C және 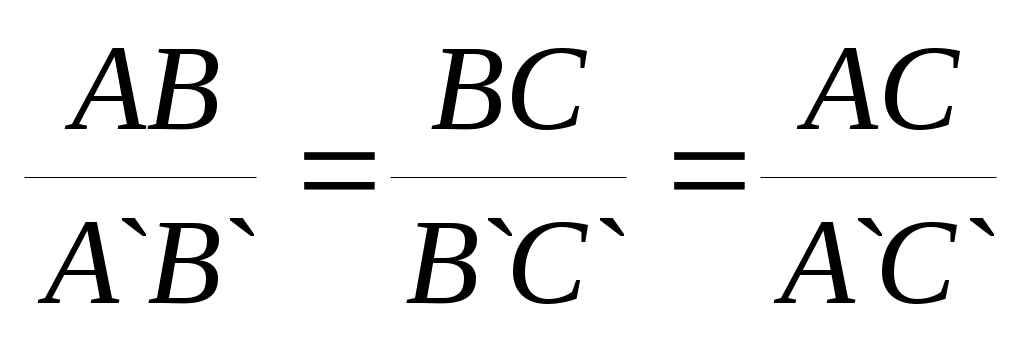 .
.
Салу есептерін шешуде ұқсас түрлендіруді қолдану ұқсас түрлендіру әдісі деп аталады. Геометриялық салуларда ұқсас түрлендіру әдісін былай қолданады: алдымен берілгеніндегі бір шарттан басқаларының бәрін қанағаттандыратын фигура салынады, содан соң ізделінді фигура салынған фигураға ұқсас және қалған бір шартты қанағаттандыратындай етіп тұрғызылады. Ұқсас түрлендіру әдісі, көбіне, есептің берілгеніндегі фигуралардың біреуі кесінді, қалғандары не бұрыштар, не кесінділердің қатынастары болған жағдайда қолданылады. Әдетте, көмекші фигураның ізделінді фигурамен ұқсастығын сақтай отырып, оны ізделінді фигурамен орналасуы да ұқсас болатындай етіп тұрғызамыз.
Мысал: (а, в) бұрышы және осы бұрыш ішінде жататын М нүктесі берілген. М нүктесі арқылы өтіп, бұрыш қабырғаларымен жанасатын шеңбер салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, (О, ОМ) – ізделінді шеңбер (36-сурет).
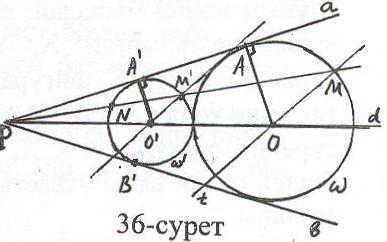
(О, ОМ) а = А, (О, ОМ) в = В деп белгілейік. Сонда ОА = ОВ = ОМ, ОА а, ОВ в. Демек ізделінді шеңбердің
центрі берілген бұрыштың биссектрисасында
жатады. Сонымен ізделінді шеңбер екі шарт-
ты қанағаттандырады:
а) (О,ОМ) шеңбері М нүктесі арқылы өтеді
б) (О,ОМ) шеңбері (а, в) бұрышының қа-
бырғаларымен жанасады, ондай шеңберлер шексіз көп және олардың центр-лері, жоғарда көрсеткеніміздей, берілген бұрыштың биссектрисасында жатады.
а), б) шарттары бойынша гомотетияны пайдаланып, салу жоспарын былайша құрамыз.
Салу: 1) (а, в)-ң М нүктесі жатқан бұрышының биссектрисасы: d
2) а) шартын қанағаттандыратын кез-келген (О, ОА) шеңбері
3) а в = Р нүктесі
4) РМ = М нүктесі
5) Р нүктесіне қатысты гомотетияда шеңберінің образы: (О,ОМ)
шеңбері (мұнда ОМОМ)
- ізделінді шеңбер
Ескерту: Салу жоспарының 5) қадамын былайша ашып жазуға болады:
5.а) ОМ түзуі
5.б) ОМ түзуіне М нүктесі арқылы параллель түзу: t
5.в) t d = О нүктесі
5.г) w(О, ОМ) – ізделінді шеңбер болады.
Дәлелдеу: Салу бойынша О¢М¢½½ОМ болғандықтан, ÐРМ¢О¢ = ÐРМО және ÐМ¢О¢Р = ÐМОР, ал ÐР бұрышы екі үшбұрышқа ортақ. Онда
DРМ¢О¢
DРМО Þ ОМ = к×О¢М¢
Олай болса, ОА = OM = k×O¢M¢ = k×O¢A¢. Сонда гомотетияда О¢А¢®ОА, ал бұл ОА ^ а шартының орындалатындығын көрсетеді. Дәл осылайша ОВ ^ в екені шығады. Онда w(О, ОМ) шеңбері бұрыш қабырғаларымен жанасады. Ал салу бойынша w шеңбері М нүктесі арқылы өтеді. Демек, а), б) шарттары орындалады.
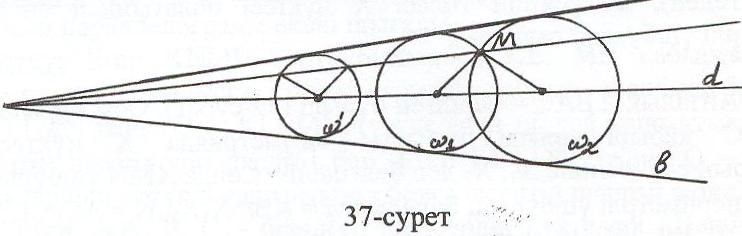
Зерттеу: 1) – 3) салу қадамдары әрдайым орындалады және бірмәнді. 4) қадамындағы РМ Ç w¢ қимасы екі нүктенің қосынан құралады. Осы нүктелердің әрқайсысы үшін салу жоспары бөлек орындалады да, есептің екі шешімі болады (37-сурет).
2.6.Түрлендірулер әдісімен шешілетін геометриялық
салуларға мысалдар
Есеп 1: Берілген кесіндіге тең әрі параллель болатын және ұштары берілген шеңбер мен берілген түзуде жататындай кесінді салыңыз.
Шешуі:
Талдау: Ізделінді кесінді салынды делік, АА = а, ААа, Аt, A,
м
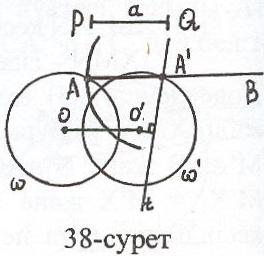
ұндағы а – берілген кесінді, - берілген шеңбер, t – берілген түзу (38-сурет). Онда А=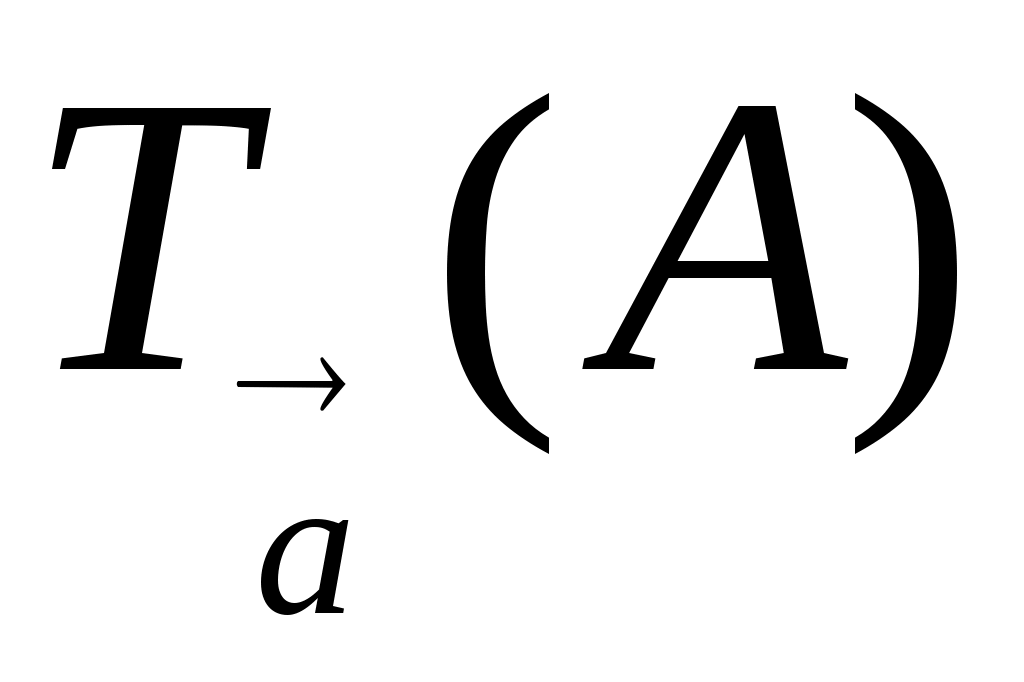 . Олай болса, логикалық ой - тұжырымдау арқылы А болады. Бұдан
. Олай болса, логикалық ой - тұжырымдау арқылы А болады. Бұдан 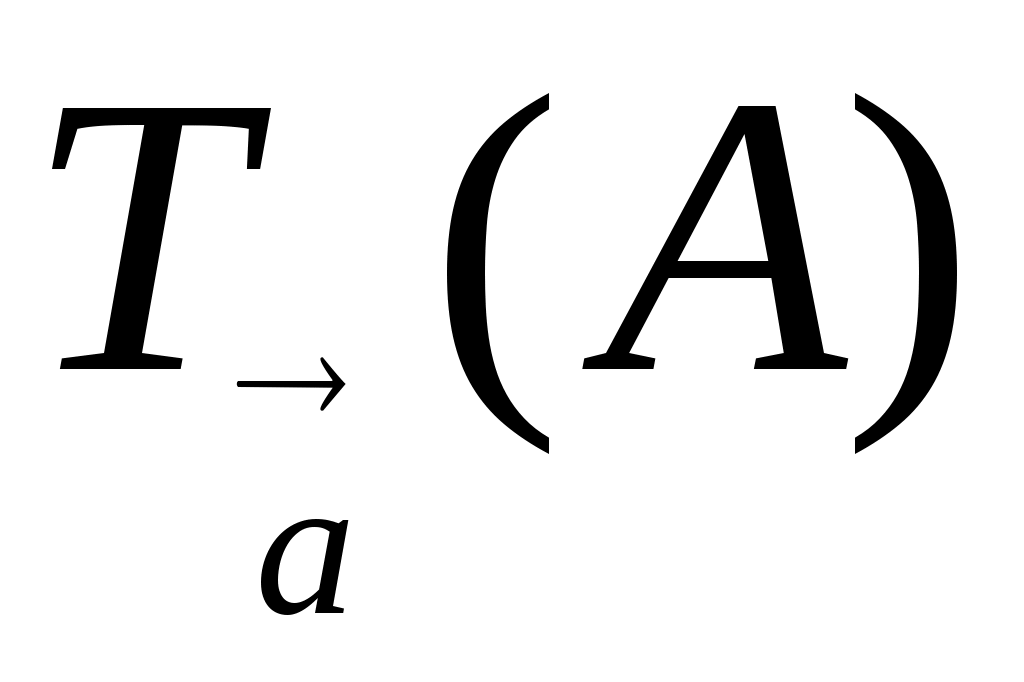
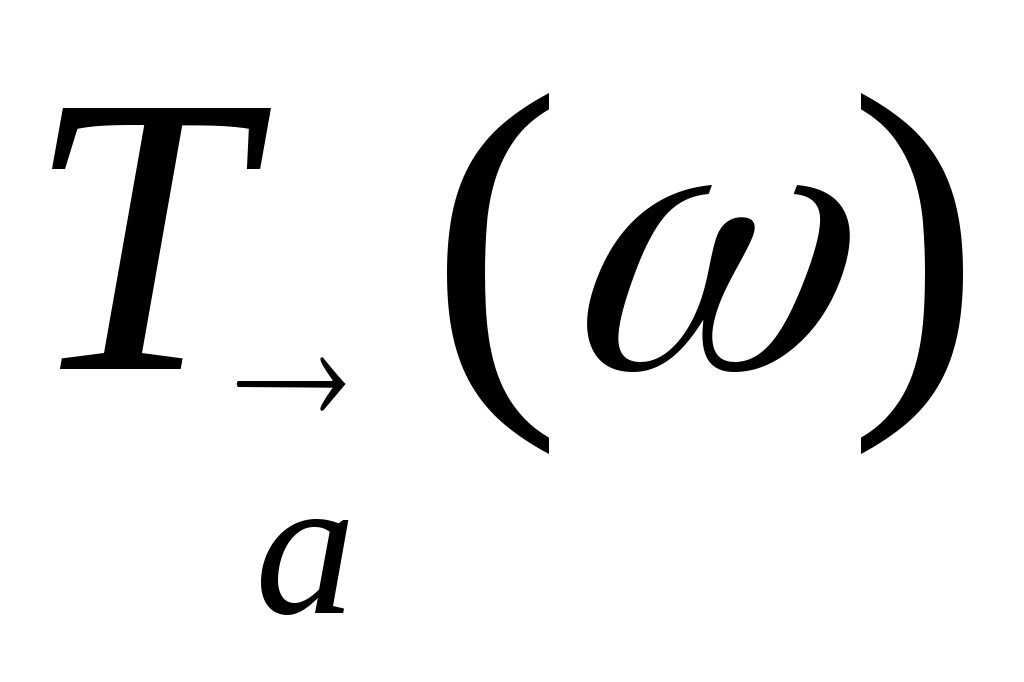 , яғни А (мұндағы
, яғни А (мұндағы 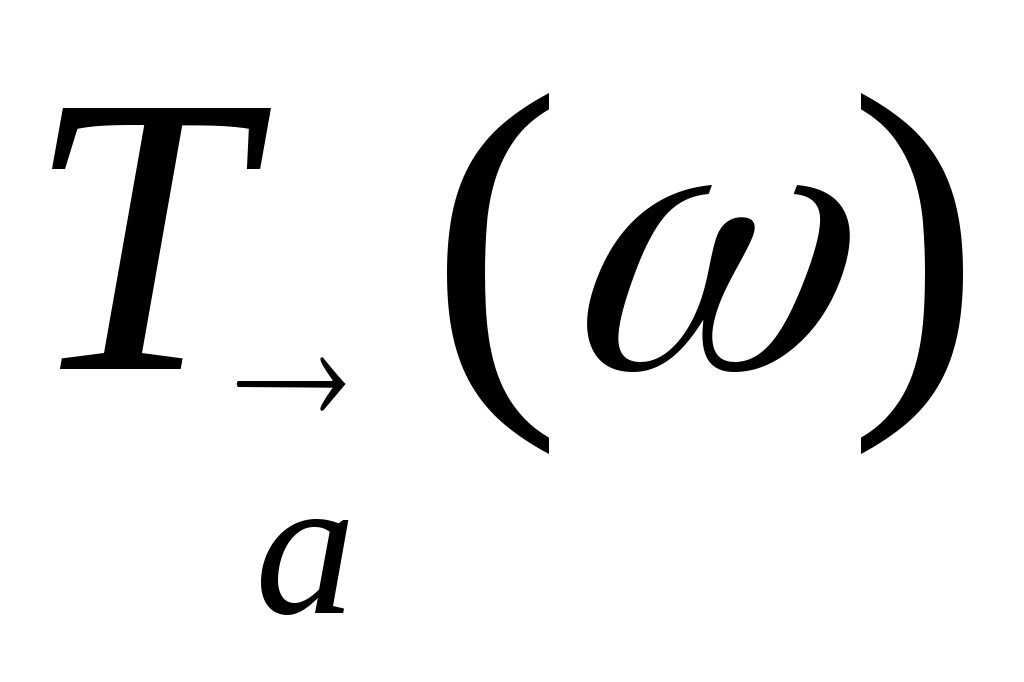 ) және А t шарты бойынша А t
) және А t шарты бойынша А t
Салу: 1) 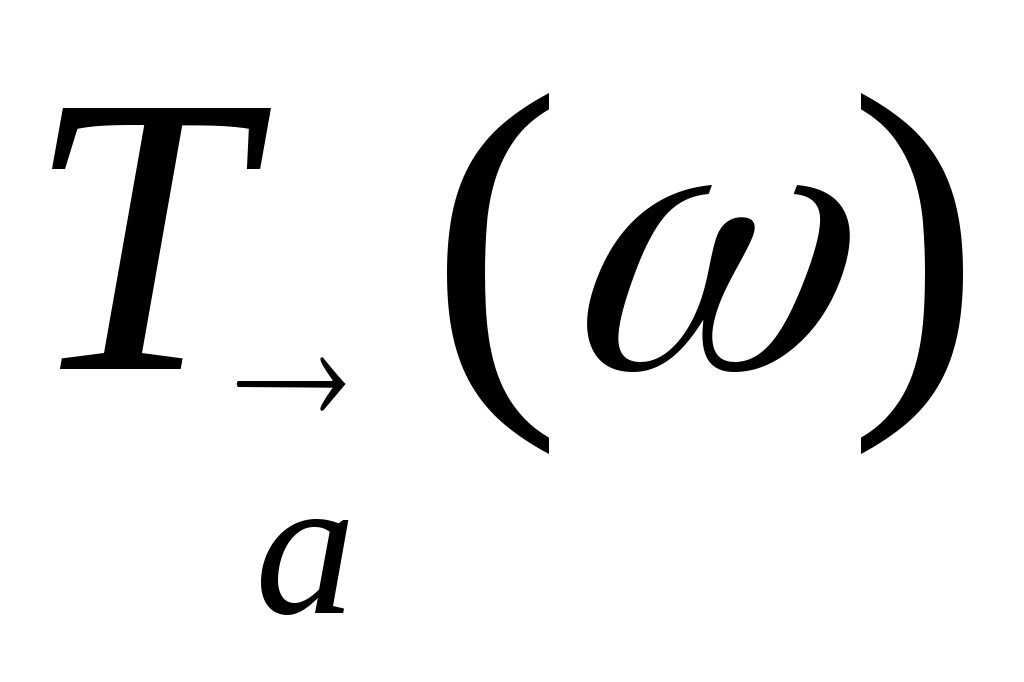 шеңбері
шеңбері
2) А = t нүктесі
3) (А, а) шеңбері
4) АВа түзуі
5) АВ = А нүктесі
6) АА кесіндісі
АА - ізделінді кесінді.
Дәлелдеу: Салу бойынша АА=а, Аt, A. ААВ және АВа ААа.
Зерттеу: 1) қадам әрдайым бірмәнді орындалады. 2) қадам орындалу үшін О нүктесінен t түзуіне дейінгі қашықтық r – дан кіші немесе тең болу керек, мұнда О, r – сәйкесінше шеңберінің центрі мен радиусы. Егер h(О, t) r болса, онда t қимасы А және А нүктелерінен құралады да, осы нүктелердің әрқайсысы үшін салу қадамдары жеке орындалады. Бұл жағдайда есептің екі шешімі бар. Егер h(О, t) = r болса, онда t қимасы жалғыз А нүктесінен құралады да, есептің бір ғана шешімі болады. Егер h(О, t) r болса, онда t = , яғни есептің шешімі жоқ.
Есеп 2: А 900 бұрышы және оның ішінен кез-келген Х нүктесі берілген. Екі төбесі берілген бұрыш қабырғаларында (әр қабырғада бір нүктеден), ал үшінші төбесі Х нүктесі болатындай ең кіші периметрлі үшбұрыш салыңыз.
Шешуі:
Талдау: Айталық ВАС – берілген бұрыш (39-сурет). Осы бұрыштың АВ, АС
қ
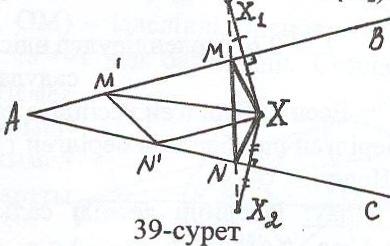
абырғаларына қатысты симметрияда Х нүктесінің образдарын сәйкесінше Х1, Х2 деп белгілейік. Сонда ХМN үшбұрышы ең кіші периметрлі үшбұрыш болады (М = AB X1X2, N = AC X1X2).
Салу: 1) SАВ: ХХ1 нүктесі
2) SАС: ХХ2 нүктесі
3) Х1Х2 түзуі
4) Х1Х2 АВ = M нүктесі
5) Х1Х2 АС = N нүктесі
6) ХМ, XN кесінділері
ХМN – ізделінді үшбұрыш.
Дәлелдеу: 4), 5) салу қадамдарынан МАВ, NАС екені шығады. Енді ХМN үшбұрышының периметрі ең кіші екенін дәлелдеу керек. МАВ және NАС болатындай кез-келген МN түзуін жүргізсек, МХ1 = MX және NX = NX2, себебі АВ – ХХ1, ал АС – ХХ2 кесіндісінің орта перпендикулярлары. Онда
РXMN = XM + MN + NX = X1M + MN + NX2 = X1X2 – түзу
РXMN = XM + MN + NX = X1M + MN + NX2 – сынық сызық
Сонда РXMN РXMN .
Зерттеу: Есеп шарты бойынша Х нүктесі ВАС бұрышының ішінде жатқандықтан, оған АВ, АС түзулеріне қарағандағы симметриялы нүктелер табылады және олар біреуден ғана болады. Олай болса, М, N нүктелері де жалғыз, себебі екі түзу бір нүктеде ғана қиылысады. Онда XMN үшбұрышы – есеп шартын қанағаттандыратын жалғыз шешім.
Есеп3: Төртбұрыштың қарама – қарсы қабырғаларынан екі нүкте алынған. Осы нүктелер төбесі болатындай берілген төртбұрышқа іштей параллелограмм сызыңыз.
Шешуі:
Талдау: Есеп шешілді делік, АВСD – ізделінді параллелограмм (40 – сурет). А, С – сәйкесінше КN, ML қабырғаларындағы берілген нүктелер. D, В нүктелері АС кесіндісінің ортасы болатын О нүктесіне қатысты симметриялы нүктелер (параллелограмның қасиеті бойынша). D MN, онда В MN.
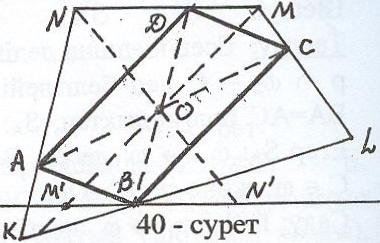
Салу: 1) О – АС кесіндісінің ортасы
2) S0: MN MN нүктесі
3) MN KL = B нүктесі
4) S0: В D нүктесі
5) АD, DC, CB, AB кесінділері
АВСD–ізделінді параллелограмм
Дәлелдеу: АО = ОС және ВО = OD теңдіктерінен АВСD төртбұрышының параллелограмм екені шығады.
Зерттеу: Егер KNML төртбұрышының KL, MN қабырғаларының созындысы қиылысса, онда есептің жалғыз шешімі бар. Егер KLMN және О - KL, MN түзулерінен бірдей қашықтықта болса, есептің шексіз көп шешімі бар. Егер KLMN және О – KL, MN түзулерінен әртүрлі қашықтықта болса, есептің шешімі жоқ.
Есеп 4: А, В, С, - берілген шеңбердің нүктелері. Шеңбердің СD хордасы О нүктесінде қақ бөлінетіндей D нүктесін табыңыз, мұндағы О = AB CD.
Шешуі:
Т
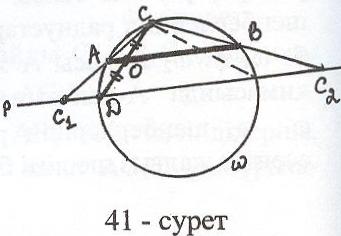
алдау: Айталық - берілген шеңбер, А , В , С және ізделінді D нүктесі тұрғызылған болсын (41-сурет). D нүктесі арқылы АВ кесіндісіне параллель болатын р түзуін жүргізіп, СА р = С1 деп белгілесек, DO = OC болғандықтан С1А = АС. Дәл осылайша
СВ р = С2 десек, С2В = ВС. Сонымен
салу жоспары мынадай болады:
Салу: 1) SA: C C1 нүктесі
2) SВ: C C2 нүктесі
3) С1С2 түзуі
4) С1С2 = D нүктесі
D – ізделінді нүкте.
Дәлелдеу: Центрлік симметрияның қасиеті бойынша СА = AC1, CB = BC2, онда АВ – С1СС2 үшбұрышының орта сызығы болады. Олай болса, АВС1С2. Салу бойынша D С1С2 болғандықтан, С1DAB және А – С1С2-ң ортасы, онда DO=OC.
Зерттеу: Төмендегідей жағдайлар болу мүмкін:
-
АВ = d, мұндағы d – берілген шеңбердің диаметрі. Егер АС = ВС болса, яғни С – АВ кесіндісінің орта перпендикулярында жатса, есептің бір шешімі болады; егер АС ≠ ВС болса, екі шешімі болады; егер С А немесе С В болса, шешімі жоқ,
-
АВ d. Егер АСВ 900 болса, есептің екі шешімі бар; АСВ 900 болса, есептің шешімі жоқ; АСВ=900 бола алмайды, себебі АВ d.
Есеп 5: 1, 2 шеңберлерінің ортақ А нүктесі арқылы берілген шеңбер-лерді бірдей хордамен қиып өтетіндей түзу жүргізіңіз.
Шешуі:
Талдау: Есеп шешілді делік, р – ізделінді түзу болсын (42-сурет). р 1 = В,
р
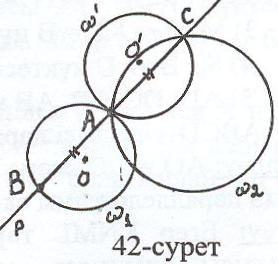
2 = C деп белгілейік. Сонда ВА = АС
болғандықтан, SA: B C. Егер SA: 1
десек, В 1 С және де С 2.
Салу: 1) SA: 1 шеңбері
2) 2 = C (А – дан өзге нүкте)
3) АС түзуі
АС – ізделінді түзу
Дәлелдеу: О1, О - сәйкесінше 1, шеңберлерінің центрлері, ал В=AC1 деп белгілейік. Центрлік симметрияның қасиеті бойынша ВО1 = O1A=AO=OC
Бұдан ОАС = О1АВ – вертикаль бұрыштар. Онда АОС = АО1В. Үшбұрыштар теңдігінің бірінші белгісі бойынша СОА = ВО1А, олай болса АВ = АС.
Зерттеу: Салу жоспарының 1) және 3) қадамдары бірмәнді орындалады, ал 2) қадамға байланысты мына жағдайлар болу мүмкін:
а) 1 2 қимасы жалғыз А нүктесінен құралады, яғни бұл шеңберлер А нүктесінде жанасады. Онда 2 қимасы да жалғыз А нүктесінен құралады. Бұл жағдайда егер 1, 2 шеңберлерінің радиустары тең болса, есептің шексіз көп шешімі бар; егер 1, 2 шеңберлерінің радиустары әртүрлі болса, есептің шешімі жоқ.
б) 1 2 қимасы А және А нүктелерінен тұрады. Онда 2 қимасында А-дан өзге бір ғана нүкте бар. Сондықтан бұл жағдайда 1, 2 шеңберлерінің радиустары тең болса да, әртүрлі болса да есептің жалғыз шешімі бар.
Есеп 6: ВАС = бұрышы, қабырғаларының АВАС = mn қатынасы және АН биіктігі бойынша АВС үшбұрышын салыңыз.
Шешуі:
Т
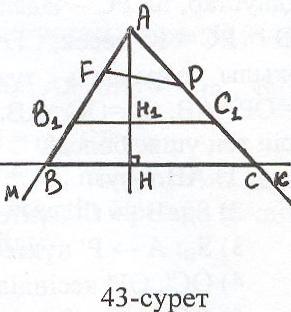
алдау: Есеп шешілді делік, яғни ізделінді АВС үшбұрышы салынған болсын (43 - сурет). Берілген бұрышты МАК деп белгілесек, онда кез – келген ҒАР (ҒМА, РКА) үшбұрышы есептің бірінші шартын қанағаттандырады. Екінші шарттын қанағаттандыратын үшбұрышты табу үшін ұқсастықты пайдала-намыз. АМ сәулесіне АВ1 = m, АK сәулесіне AC1 = n кесінділерін салсақ, В1АС1
ВАС.
§2. Түрлендірулер әдісі
Айталық жазықтықтағы Ф фигурасының әрбір М нүктесіне осы жазықтықтың қандай да бір анықталған М' нүктесін сәйкестендіретіндей ереже орнатылған болсын. Онда жазықтықта Ф фигурасының түрлендіруі берілген делінеді. М' - М нүктесінің образы, ал М - М' нүктесінің прообразы деп аталады. Берілген Ф фигурасының нүктелеріне сәйкестендірілген нүктелер жиыны Ф' фигурасын құрайды және ол фигураны Ф-ң образы деп атайды.
Түрлендіруді геометриялық салулар теориясында қолдану геометриялық турлендірулер әдісі деп аталады. Түрлендірулер әдісінің негізгі мақсаты – берілген немесе ізделінді фигураларды түрлендіре отырып, есепті оңай шешілетіндей қарапайым түрге келтіру. Көптеген салу есептерін шешуде жазықтықты геометриялық түрлендіру нәтижелі қолданылады. Енді солардың түрлеріне тоқталып өтейік.
2.1. Параллель көшіру әдісі
Параллель көшіру, көрнекі түрде, нүктелері бір бағытта, бірдей арақа-шықтыққа көшірілетін түрлендіру деп түсіндіріледі.
Жазықтықта декарттық координаталар системасын енгіземіз. Кез - келген (х, у) нүктесі жазықтықтың (х+а, у+в) нүктесіне көшетіндей Ғ фигурасын түрлендіру параллель көшіру деп аталады, мұндағы а,в сандары барлық (х,у) нуктелері үшін бірдей. Параллель көшіру х'=х+а, у'=у+в формулаларымен беріледі. Бұл формулалар параллель көшірудегі (х,у) нүктесі көшетін нүктенің х', у' координаталарын көрсетеді (21-сурет).

Параллель көшіру – қозғалыс.
Параллель көшіруде нүктелер параллель (немесе беттесетін) түзулер бойымен бірдей қашықтыққа ауысады. Параллель көшіруде түзу өзіне параллель түзуге немесе өз - өзіне көшеді.
Параллель көшіруді геометриялық салуларда қолдану параллель көшіру әдісі деп аталады. Осы әдіс бойынша есепті шешуге берілген немесе ізделінді фигураларды не олардың элементтерін параллель көшіруден пайда болған фигуралар қарастырылады. Бұл есепке талдау жасауды барынша жеңілдетеді.
Параллель көшіру әдісі фигураның «шашыраңқы» бөліктерін біріктіруде, көпбұрыштарды (әсіресе, төртбұрыштарды) салуда жиі қолданылады. Мұнда, әдетте, бір немесе бірнеше кесінділердің параллель көшірудегі образдарын қарастыру арқылы салуды жеңілдететін қосымша фигуралар (мысалы, үшбұрыш) қарастырылады.
Мысал: Берілген төрт қабырғасы бойынша трапеция салыңыз.
Шешуі:
Т

алдау. Есеп шешілді делік, яғни ізделінді АВСД трапециясы тұрғызылған. АD = а – үлкен табан, ВС = в – кіші табан, ал АВ = d және СD = c – бүйір қабырғалар.(22-сурет)
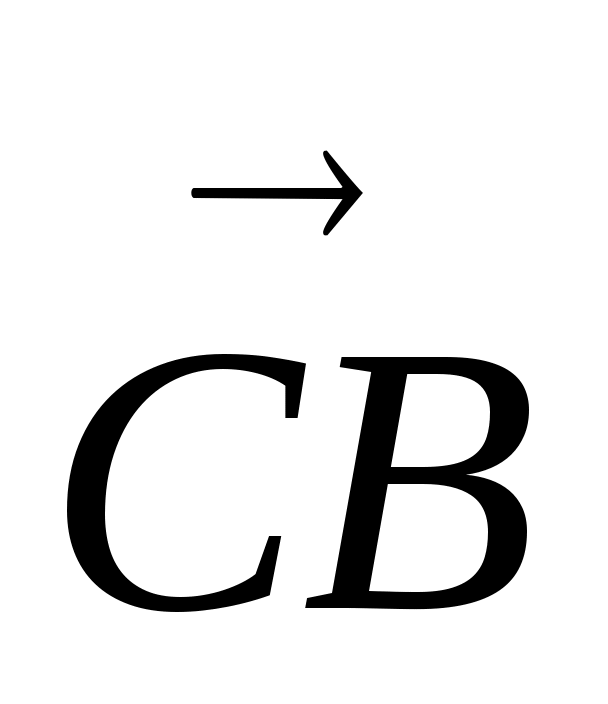 векторына қатысты параллель көшіру
векторына қатысты параллель көшіру
қарастырайық. Сонда СD қабырғасы ВD'
(D' АD) қабырғасына көшеді. АВD' үшбұ-
АD) қабырғасына көшеді. АВD' үшбұ-
рышын берілген үш қабырғасы бойынша
салу оңай. Онда ізделінді трапецияны салу
үшін ВD' кесіндісін  векторы бағытымен, ұзындығы в–ға тең болатындай қашықтыққа параллель көшіреміз.
векторы бағытымен, ұзындығы в–ға тең болатындай қашықтыққа параллель көшіреміз.
Салу. 1) АВ = d, ВD' = с, АD' = а - в қабырғалары бойынша АВD' үшбұрышы
2) АD' түзуі
3) АD = а кесіндісі, А-D'-D және D AD'
4) ТД'Д : ВD'→СD кесіндісі
5) ВС кесіндісі
АВСD - ізделінді трапеция
Дәлелдеу. Салу бойынша АD = а, АВ = d, алпараллель көшірудің қасиеті бойынша СD = с, ВС AD. Сонда ВС = DD' = АD - АD' = а - (а – в) = в.
Зерттеу. Егер СD – АВ < АD – ВС < СD + АВ қатынасы орындалса, есептің бір ғана шешуі бар. Қалған жағдайларда есептің шешімі жоқ.
2.2. Осьтік симметрия әдісі

Айталық р - берілген түзу. Кез-келген Х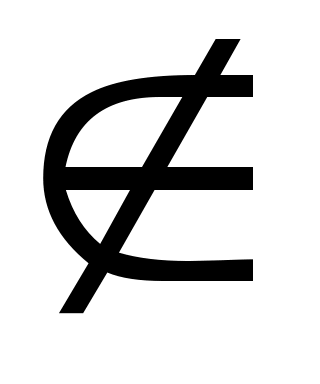 р нүктесінен р түзуіне АХ перпендикулярын (А
р нүктесінен р түзуіне АХ перпендикулярын (А р) түсіреміз (23-сурет). Осы перпендикулярдың созындысына А нүктесінің екінші жағынан
р) түсіреміз (23-сурет). Осы перпендикулярдың созындысына А нүктесінің екінші жағынан
АХ - қа тең АХ' кесіндісін салсақ, Х' р
түзуіне қарағанда Х нүктесіне симметриялы
нүкте болады. Егер Х р болса, онда оған р
р болса, онда оған р
түзуіне қатысты симметриялы нүкте өзі болады.

Әрбір Х нүктесі с түзуіне қарағанда симметриялы Х' нүктесіне көшетіндей Ғ фигурасын Ғ' фигурасына түрлендіру осьтік симметрия деп аталады. Мұндағы, Ғ, Ғ' – с түзуіне қатысты симметриялы фигуралар (24-сурет). Егер осьтік симметрияда Ғ фигурасы өз-өзіне
көшсе, онда оны түзуге қатысты симмет-
риялы фигура деп атайды, ал с – оның
симметрия осі болады.(25-сурет)
Осьтік симметрия – қозғалыс.

Салу есептерін шешу барысында осьтік симметрияның қасиеттері қолданылуы мүмкін. Мұндай жағдайда анализде берілген фигураға, не оның элементіне қандай да бір түзуге қатысты симметриялы фигура салып аламыз. Нәтижесінде оңай шешілетін немесе қарапайым түрдегі «жаңа» есеп алынады.
Осьтік симметрияны қолдану сызықтарды түзумен алмастыруға, берілген фигураның «шашыраңқы» элементтерін жақынтуға мүмкіндік береді.
Мысал: Қос-қостан қиылысатын a, в, с үш түзуі берілген. в түзуіне перпендикуляр болып, ортасы в түзуінде, ал ұштары а, с түзулерінде жататын кесінді салыңыз.
Шешуі:
Талдау. Есеп шешілді делік, АС – ізделінді кесінді (26, а) сурет). Онда А а, С
а, С с, В
с, В в және АВ=ВС, АСв. Бұдан в түзуіне қарағандағы симметрияда А нүктесі С нүктесіне немесе С нүктесі А нүктесіне көшеді.
в және АВ=ВС, АСв. Бұдан в түзуіне қарағандағы симметрияда А нүктесі С нүктесіне немесе С нүктесі А нүктесіне көшеді.
Салу. 1) Sв: а → а' түзуі
-
С = а' 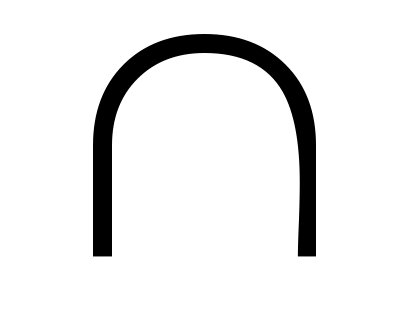 с нүктесі
с нүктесі
-
СН в түзуі
-
А = СН 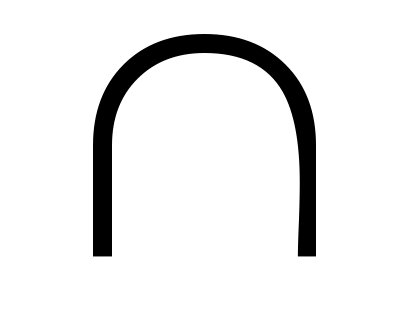 а нүктесі
а нүктесі
АС – ізделінді кесінді.
Дәлелдеу. Салуымыз бойынша АС в. Осьтік симметрияның қасиеті бойынша, в –  (а, а') бұрышының биссектрисасы болады. Ал бұдан АС в екенін ескерсек, АВ = ВС.
(а, а') бұрышының биссектрисасы болады. Ал бұдан АС в екенін ескерсек, АВ = ВС.
Зерттеу. Мынандай жағдайлар болу мүмкін:
1) с және а' түзулері қиылысады, онда есептің бір ғана шешімі бар (26,а) сурет)
2) с және а' түзулері параллель, онда есептің шешімі болмайды (26, б) сурет)


2.3. Центрлік симметрия әдісі
Айталық О – жазықтықтағы нүкте, ал Х – еркімізше алынған нүкте болсын (27-сурет). ОХ кесіндісінің созындысына О нүктесінің екінші жағынан ОХ -
қ

а тең ОХ' кесіндісін өлшеп салайық. Сонда
Х' нүктесі О нүктесіне қарағанда Х нүктесіне
симметриялы деп аталады. О нүктесіне сим -
метриялы нүкте оның өзі болады.
Ғ фигурасын оның әрбір Х нүктесі берілген О нүктесіне қарағанда симметриялы Х' нүктесіне көшетін етіп, Ғ' фигурасына түрлендіру О нүктесіне қатысты симметрия арқылы түрлендіру деп аталады (28-сурет).

Сонда Ғ және Ғ ' фигуралары О нүктесіне қатысты симметриялы фигуралар болады.
Егер О нүктесіне қарағанда центрлік симметрияда Ғ фигурасын өз-өзіне көшіретін болса, онда Ғ фигурасының симметрия центрі бар деп аталады, О нүктесі симметрия центрі болады. Мысалы, параллелограмның симметрия центрі оның диагональдарының қиылысу нүктесі болады.
Салу есептерін шешуде центрлік симметрияны қолдану центрлік симметрия әдісі деп аталады. Бұл әдіс бойынша берілген немесе ізделінді фигуралардың, не олардың кейбір элементтерінің қандай да бір нүктеге қатысты симметриялары қарастырылады. Центрлік симметрия әдісін, әдетте, фигураның немесе оның бөлігінің симметрия центрі болған жағдайда қолданған ыңғайлы.
Мысал: Бір қабырғасы, оған жүргізілген биіктігі және басқа екі қабырғаның біріне жүргізілген медианасы бойынша үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, яғни АВС - ізделінді үшбұрыш (29-сурет). Онда
В

К = mв (АК = КС), АР = ha, ВС = а. АВС
үшбұрышын параллелограмға толықтырсақ,
К нүктесіне қатысты центрлік симметрияда
В нүктесі М нүктесіне көшеді. Олай болса,
МВ = 2mв. Сонымен М нүктесі екі геометрия-
риялық орынға тиісті:
Ғ1: ω(В, 2mв) шеңберіне
Ғ2: ВС түзуінен hа қашықтықтағы АМ түзуіне
Сонда осы айтылғандарды ескере отырып, салу жоспарын былайша құра аламыз:
Салу: 1) ВС = а кесіндісі
2) ВС түзуінен hақашықтықтағы параллель түзу: l
3) ω (В, 2mв) шеңбері
4) ω (В, 2mв) ∩ l = М нүктесі
5) МВ кесіндісі
6) К – МВ кесіндісінің ортасы
7) Sк : С → А нүктесі
8) АВ түзуі
АВС – ізделінді үшбұрыш
Дәлелдеу: Салуымыз бойынша ВС = а, МВ = 2mв. Онда центрлік симмет-рияның қасиетінен ВК = mв. Бұдан ВС l болғандықтан, К осы түзулердің симметрия осінде жатады (3.1.2. Қарапайым ГО, 3)), яғни Sк : ВС → l. Олай болса, А  l, бұдан АР = hа шығады.
l, бұдан АР = hа шығады.
Зерттеу: Салу жоспарының 1) - 3) қадамдары әрдайым бірмәнді орындалады. Ал 4) салуында ω (В, 2mв) ∩ l қимасына байланысты мына жағдайлар болуы мүмкін:
а) 2mв < hа, онда ω(В, 2mв) ∩ l= болады да, есептің шешімі жоқ (30 а) сурет);
б) 2mв = hа, онда ω(В, 2mв) ∩ l қимасы бір нүктеден құралады да, есептің жалғыз шешімі болады (30 б)-сурет);
в) 2mв hа, онда ω(В, 2mв) ∩ l қимасы М және М' нүктелерінің қосынан құралады. Бұл жағдайда әр нүкте үшін салу жоспары бөлек орындалады да, есептің екі шешімі бар (30 в)-сурет).

2.4. Бұру әдісі
Берілген нүктені айналдыра жазықтықты бұру деп, осы нүктеден шыққан әрбір сәуле бір бағытта, бірдей бұрышқа бұрылатын қозғалысты айтады.

Егер О нүктесін айналдыра бұруда Х нүктесі Х' нүктесіне көшсе (31-сурет), онда Х нүктесі қандай болмасын ОХ және ОХ' сәулелері бірдей бұрыш құрайды. Бұл бұрыш бұру бұрышы деп аталды.
Бұрудың қозғалыс болатыны жеңіл дәлелденеді.
Кейбір салу есептерін шешуде бұруды пайда-
лану тиімді болады. Бұл әдістің мәнісі мынада:
талдауды жеңілдету үшін немесе есептің шешімін
бірден табу үшін фигураның кейбір элементтерін
берілген центрден берілген бұрышқа бұрады. 31 – сурет
Мысал: Параллель екі түзу және олармен шектелген жолақтан А нүктесі берілген. Екі төбесі берілген түзулерде, бір төбесі берілген нүкте болатын тең қабырғалы үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, яғни в║с, А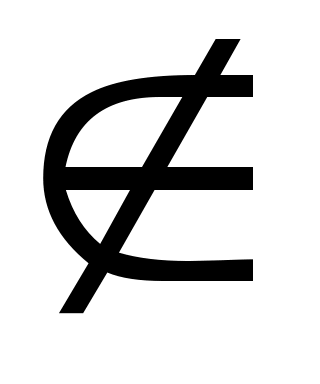 в, А
в, А 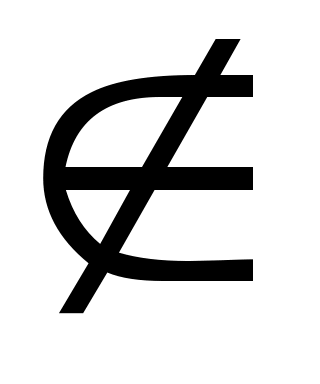 с, В
с, В в, С
в, С с, АВ = ВС = АС (32-сурет). АВС үшбұрышы дұрыс болғандықтан, А = 600 (В = С = 600). Олай болса, В төбесін 600-қа сағат тілімен бағыттас бұрсақ, ізделінді үшбұ-рыштың С төбесі шығады. Ендеше салу жоспары төмендегідей:
с, АВ = ВС = АС (32-сурет). АВС үшбұрышы дұрыс болғандықтан, А = 600 (В = С = 600). Олай болса, В төбесін 600-қа сағат тілімен бағыттас бұрсақ, ізделінді үшбұ-рыштың С төбесі шығады. Ендеше салу жоспары төмендегідей:
С

алу: 1) R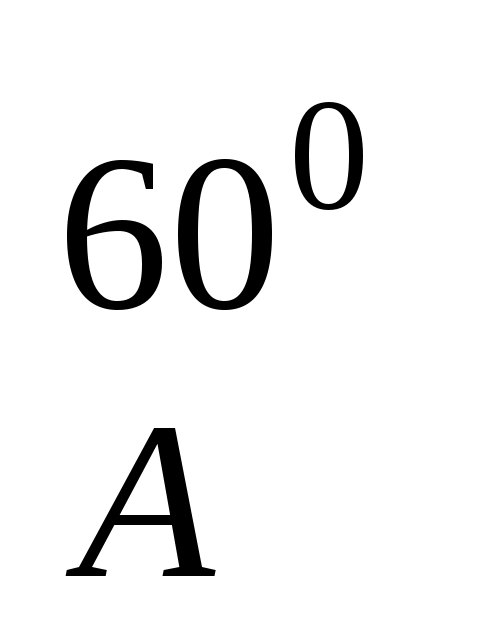 : в→в' түзуі
: в→в' түзуі
2) С = в' с нүктесі с
3) (А, АС) шеңбері
4) В = в нүктесі в
5) АВ, ВС, СА кесінділері
АВС – ізделінді үшбұрыш.
Дәлелдеу: R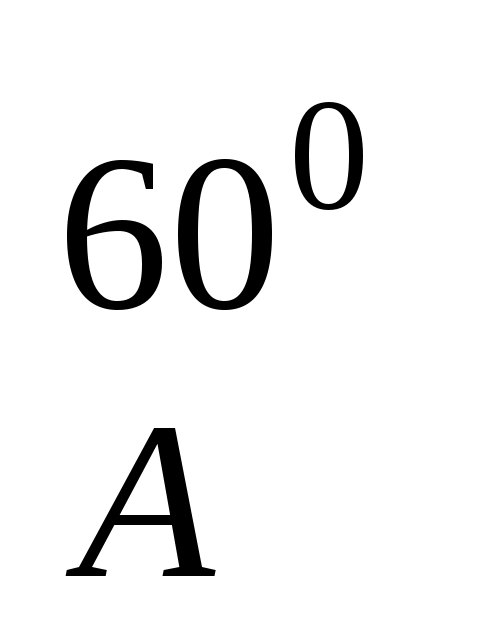 : в→в' болғандықтан АС, АВ кесінділерінің арасындағы бұрыш 600-ты құрайды, яғни САВ = 600. АС = АВ (радиустар), бұдан АСВ = АВС. Онда АСВ =
: в→в' болғандықтан АС, АВ кесінділерінің арасындағы бұрыш 600-ты құрайды, яғни САВ = 600. АС = АВ (радиустар), бұдан АСВ = АВС. Онда АСВ = 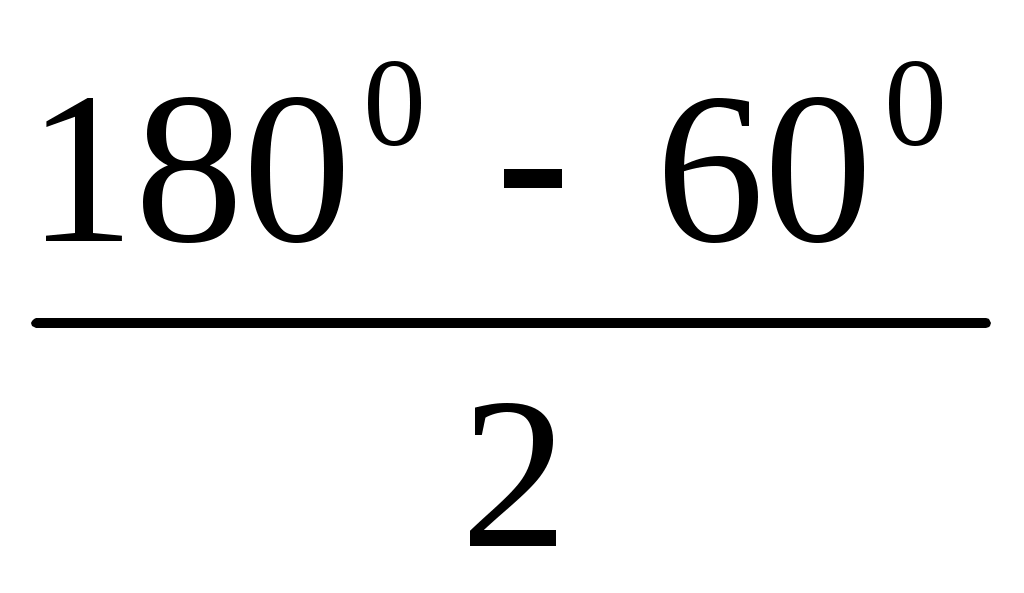 = 600. Олай болса, АВС – тең қабырғалы үшбұрыш.
= 600. Олай болса, АВС – тең қабырғалы үшбұрыш.
Зерттеу: Салу жоспарының 1) – 3) қадамдары орындалады, ал 4)-ші қадамға байланысты мына жағдайларды қарастырайық:
а) в, яғни АС АН. Онда АН = АН болғандықтан АС АН. Бірақ бұлай болу мүмкін емес, себебі АСН үшбұрышында АС – гипотенуза. Сонда шеңбері мен в түзуі міндетті түрде қиылысады (33-сурет).
б

) в қимасы бір нүкте – В нүктесі, онда АС=АН.
Бұдан АС=АН, бірақ тікбұрышты үшбұрышта гипо-
тенуза мен катет тең болуы мүмкін емес.
в) в қимасы В және В нүктелерінен құралған.
Осы екі нүктенің біреуі үшін ғана салу жоспары
орындалады, себебі САВ ≠ САВ. Сонымен
есептің жалғыз шешімі болады.
2.5. Ұқсас түрлендіру әдісі
Егер Ғ фигурасын Ғ фигурасына түрлендіргенде нүктелердің арақашық-тығы бірдей сан есе өзгеретін (артады немесе кемиді) болса, онда мұндай түрлендіру ұқсас түрлендіру деп аталады.
Е

гер Ғ фигурасының еркімізше алынған Х, У нүктелері ұқсас түрлендіргенде Ғ фигурасының Х, У нүктелеріне көшсе, онда ХУ = к∙ХУ болады (34-сурет), мұндағы к – Х, У нүктелері үшін бірдей сан.
к саны ұқсастық коэффиценті деп аталады.
к=1 болғанда ұқсас түрлендіру – қозғалыс.
Айталық Ғ берілген фигура және О – бел-
гіленген нүкте. Ғ фигурасының кез-келген Х
нүктесі арқылы ОХ сәулесін жүргізіп, оған
к

∙ОХ оң санына тең ОХ кесіндісін белгілейміз. Осы «заңдылық» бойынша әрбір Х нүктесі Ғ фигурасының Х нүктесіне көшетін Ғ фигурасын Ғ–қа түрлендіруді О центріне қатысты гомотетия деп атайды, ал к – гомотетия коэффиценті болады (35 – сурет).
Ұқсас түрлендіру түзуді түзуге, жарты түзуді жарты түзуге, кесіндіні кесіндіге көшіреді. Ұқсас түрлендіруде жарты түзулердің арасындағы бұрыш сақталады.
Ұқсас түрлендіру арқылы бір – біріне көшірілетін фигуралар ұқсас деп аталады. Ұқсас көпбұрыштардың сәйкес бұрыштары тең, ал сәйкес кесінділері пропорционал. Мысалы, ΔАВС
ΔА′В′С′ болса, онда А = A, B = B, C = C және С = а'
СН в түзуі
А = СН
Салу есептерін шешуде ұқсас түрлендіруді қолдану ұқсас түрлендіру әдісі деп аталады. Геометриялық салуларда ұқсас түрлендіру әдісін былай қолданады: алдымен берілгеніндегі бір шарттан басқаларының бәрін қанағаттандыратын фигура салынады, содан соң ізделінді фигура салынған фигураға ұқсас және қалған бір шартты қанағаттандыратындай етіп тұрғызылады. Ұқсас түрлендіру әдісі, көбіне, есептің берілгеніндегі фигуралардың біреуі кесінді, қалғандары не бұрыштар, не кесінділердің қатынастары болған жағдайда қолданылады. Әдетте, көмекші фигураның ізделінді фигурамен ұқсастығын сақтай отырып, оны ізделінді фигурамен орналасуы да ұқсас болатындай етіп тұрғызамыз.
Мысал: (а, в) бұрышы және осы бұрыш ішінде жататын М нүктесі берілген. М нүктесі арқылы өтіп, бұрыш қабырғаларымен жанасатын шеңбер салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, (О, ОМ) – ізделінді шеңбер (36-сурет).

(О, ОМ) а = А, (О, ОМ) в = В деп белгілейік. Сонда ОА = ОВ = ОМ, ОА а, ОВ в. Демек ізделінді шеңбердің
центрі берілген бұрыштың биссектрисасында
жатады. Сонымен ізделінді шеңбер екі шарт-
ты қанағаттандырады:
а) (О,ОМ) шеңбері М нүктесі арқылы өтеді
б) (О,ОМ) шеңбері (а, в) бұрышының қа-
бырғаларымен жанасады, ондай шеңберлер шексіз көп және олардың центр-лері, жоғарда көрсеткеніміздей, берілген бұрыштың биссектрисасында жатады.
а), б) шарттары бойынша гомотетияны пайдаланып, салу жоспарын былайша құрамыз.
Салу: 1) (а, в)-ң М нүктесі жатқан бұрышының биссектрисасы: d
2) а) шартын қанағаттандыратын кез-келген (О, ОА) шеңбері
3) а в = Р нүктесі
4) РМ = М нүктесі
5) Р нүктесіне қатысты гомотетияда шеңберінің образы: (О,ОМ)
шеңбері (мұнда ОМОМ)
- ізделінді шеңбер
Ескерту: Салу жоспарының 5) қадамын былайша ашып жазуға болады:
5.а) ОМ түзуі
5.б) ОМ түзуіне М нүктесі арқылы параллель түзу: t
5.в) t d = О нүктесі
5.г) w(О, ОМ) – ізделінді шеңбер болады.
Дәлелдеу: Салу бойынша О¢М¢½½ОМ болғандықтан, ÐРМ¢О¢ = ÐРМО және ÐМ¢О¢Р = ÐМОР, ал ÐР бұрышы екі үшбұрышқа ортақ. Онда
DРМ¢О¢
АВ = d, мұндағы d – берілген шеңбердің диаметрі. Егер АС = ВС болса, яғни С – АВ кесіндісінің орта перпендикулярында жатса, есептің бір шешімі болады; егер АС ≠ ВС болса, екі шешімі болады; егер С А немесе С В болса, шешімі жоқ,
АВ d. Егер АСВ 900 болса, есептің екі шешімі бар; АСВ 900 болса, есептің шешімі жоқ; АСВ=900 бола алмайды, себебі АВ d.
Салу: 1) МАК = бұрышы
2) АВ1 = m (В1АМ) кесіндісі
3) АС1 = n (С1АК) кесіндісі
4) В1С1 кесіндісі
5) АН1 В1С1 (Н1 В1С1) түзуі
6) АН1 сәулесіне АН = h кесіндісі
7) Н нүктесі арқылы lВ1С1 түзуі
8) l МА = В нүктесі
9) l КА = С нүктесі
АВС – ізделінді
Дәлелдеу: Салу бойынша АВ1С1 үшбұрышында В1АС1 = , АВ1АС1 = mn және ВСВ1С1. Онда АВС АВ1С1 (үшбұрыштың қабырғасына параллель түзу оған ұқсас болатын үшбұрыш қияды). Олай болса, АВС үшбұрышында да ВАС = , АВАС = mn және де салу бойынша А төбесінен түсірілген биіктік h болады. Демек АВС үшбұрышы есептің барлық шартын қанағаттандырады, яғни ізделінді болады.
Есеп 7: АВС сүйір бұрышты үшбұрышының ішінен А, В, С нүктелеріне дейінгі қашықтықтарының қосындысы ең кіші болатындай О нүктесін табыңыз.
Шешуі:
Т
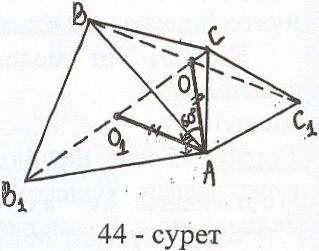
алдау: Ізделінді О нүктесі тұрғызылған болсын (44-сурет). АВО үшбұрышын АВС үшбұрышының сыртына қарай 600-қа бұрсақ, О О1, В В1. АО = АО1, О1АО = 600, бұдан АО1О – тең қабырғалы үшбұрыш, яғни АО = ОО1. Егер В1, О1, О, С нүктелері бір түзудің бойында жатса, В1О1ОС сызығы ең кіші ұзындыққа ие болады. Осылайша О В1С. Дәл осы әдіспен О С1В, мұндағы С1 -
Салу: 1) АВС үшбұрышының сыртынан
АВ, АС кесінділеріне, сәйкесінше,
тең қабырғалы АВ1В және АС1С
үшбұрыштарын тұрғызамыз.
2) В1С және С1В түзулері
3) В1С С1В = О нүктесі
О – ізделінді нүкте.
Дәлелдеу: Дәлелдеуі талдаудан байқауға болады.
Зерттеу: Қабырғалары АВ, АС болатын тең қабырғалы үшбұрыштар әрдайым бірмәнді табылады. Олай болса, В1С С1В = О нүктесі де жалғыз, яғни есептің бір ғана шешімі бар.
Есеп 8: Шеңбердің екі радиусы сызылған. Осы радиустармен тең үш бөлікке бөлінетіндей шеңбердің хордасын салыңыз.
Шешуі:
Талдау: Айталық (О, r) – берілген шеңбер, АО, ВО – берілген радиустар, ал РС – ізделінді кесінді (45-сурет). Онда АО РС = D, ВО РС = К десек, CD=DK=KP. РС кесіндісіне А (немесе В) нүктесі арқылы параллель түзу жүргізсек, РОС = РОС, мұндағы Р = ОР АВ, С = ОС АВ. Олай болса, АО, ВО радиустары РС кесіндісін тең үшке бөледі.
С
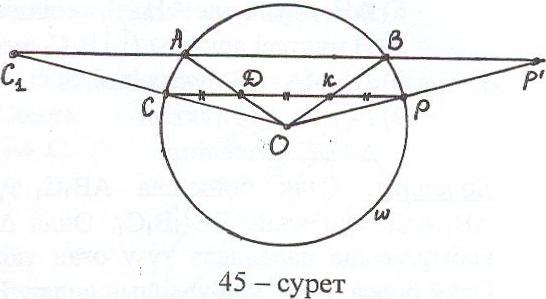
алу: 1) АВ түзуі
2) SA: В С нүктесі
3) SВ: А Р′ нүктесі
4) ОС, ОР кесінділері
5) ОС = С нүктесі
6) ОР = Р нүктесі
7) РС кесіндісі
РС – ізделінді кесінді
Дәлелдеу: АО, ВО радиустар болғандықтан, ОАС = ОВР. Салу бойынша АС = ВР. Онда АСО = ВРО, бұдан СО = РО. ОС мен ОР радиустар болғандықтан тең, онда СС = РР. Бұдан РСРС, яғни РОС РОС. Ал салу бойынша СА = AB = ВР, онда үшбұрыштардың ұқсастығынан CD = =DK=KP.
Зерттеу: Егер А, В нүктелері О нүктесіне қатысты симметриялы емес болса, онда есептің бір ғана шешімі бар. Егер А, В нүктелері О нүктесіне қатысты симметриялы болса, есептің шешімі болмайды.
Есеп 9: Үш медианасы ma, mв, mc бойынша үшбұрыш салыңыз.
Шешуі:
Т
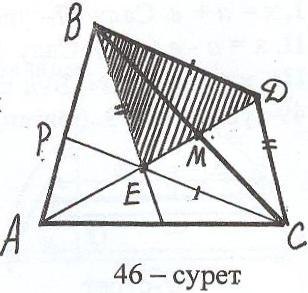
алдау: Есеп шешілді делік және ізделінді АВС үшбұрышы тұрғызылған болсын (46-сурет). АМ, ВN және СР – оның медианалары, Е – медианалардың қиылысу нүктесі және АМ = ma, BN = mв, CP = mc. ВЕС үшбұрышында ВЕ=
Салу: 1)ВЕ =
қабырғалары бойынша ΔВЕD
2) М – ЕD кесіндісінің ортасы
3) SM: В С нүктесі
4) SЕ: D A нүктесі
5) АВ, ВС, СА кесінділері
АВС – ізделінді үшбұрыш
Дәлелдеу: Салу бойынша ЕD =
a шығады. М – ЕD кесіндісінің ортасы және SM: В С бойынша SM:ВD СЕ, яғни BD = CE =
Зерттеу: ВЕD үшбұрышын салу үшін mа mв + mс, mв mа + mс, mс mа +mв, қатынастары орындалуы керек. Онда есептің бір ғана шешімі бар. Басқа жағдайларда есептің шеімі жоқ.
§3. Алгебралық әдіс
Кейбір геометриялық салуларда түзудің қандай да бір кесіндісін тұрғызу керектігі айтылады. Ондай есептерді шешу үшін алгебралық әдісті қолданамыз.
Алгебралық әдіс бойынша берілген кесінділердің ұзындықтары а, в, с, ... әріптерімен, ізделінді кесіндінің ұзындығы х әрпімен белгіленіп алынады да, есеп шартын пайдалана отырып ізделінді кесінділердің ұзындығын берілгендермен байланыстыратындай теңдеу құрылады. Құрылған теңдеуді шешіп, х-тің табылған өрнегінің геометриялық кескінін саламыз. Бұл – ізделінді кесінді болады.
Кейбір кесінділерді (немесе бірнеше кесінділерді) салу арқылы салу есептерін шешу алгебралық әдіс деп аталады. Салу есептерін шешудің алгебралық әдісі төмендегі алгоритм арқылы іске асады:
-
теңдеу құру -
құрылған теңдеуді шешу -
формуланы зерттеу -
табылған кесіндіні салу.
Мысал: «Бірлік» кесінді берілген. Ұзындығы у =
3.1. Қарапайым формулалармен берілген кесінділерді салу
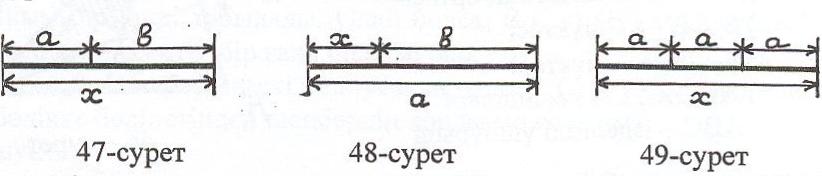
І. х = а + в Салу 47-суретте көрсетілген.
ІІ. х = а - в (а>в) Салу 48-суретте көрсетілген.
ІІІ. х = nа, n Ν. Бұл кесіндіні салу І–ші салуға келтіріледі. Мысалы 49-суретте n = 3 болған жағдай белгіленген: х = 3а.
І
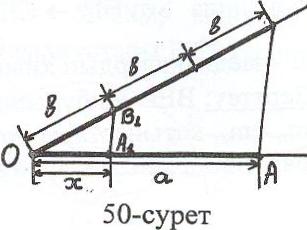
V. х =
сіндісінің екінші ұшы) қосамыз. ОВ1=вшарты
арқылы анықталатын В1 нүктесінен АВ – ға
жүргізілген параллель түзудің а кесіндісімен
қиылысуын А