Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1003
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i и vj. Из этого следует, что если вершины vi и vj не соединены рёбрами, то элемент матрицы смежности sij равен нулю.
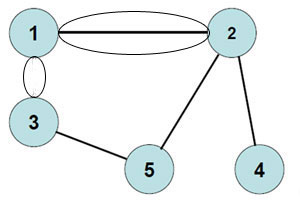
Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.
Ответ.
Матрица инцидентности H - это матрица размера n x m, где n - число вершин графа, m - число рёбер графа. Обычно в матрице инцидентности строки соответствуют вершинам графа, а столбцы - рёбрам графа.
Матрица инцидентности для неориентированного графа
Элемент матрицы инцидентности для неориентированного графа hij определяется следующим образом:
- равен единице, если вершина vi инцидентна ребру ej;
- равен нулю, если вершина vi не инцидентна ребру ej.
Пример 3. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

Ответ.
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
I вариант
А)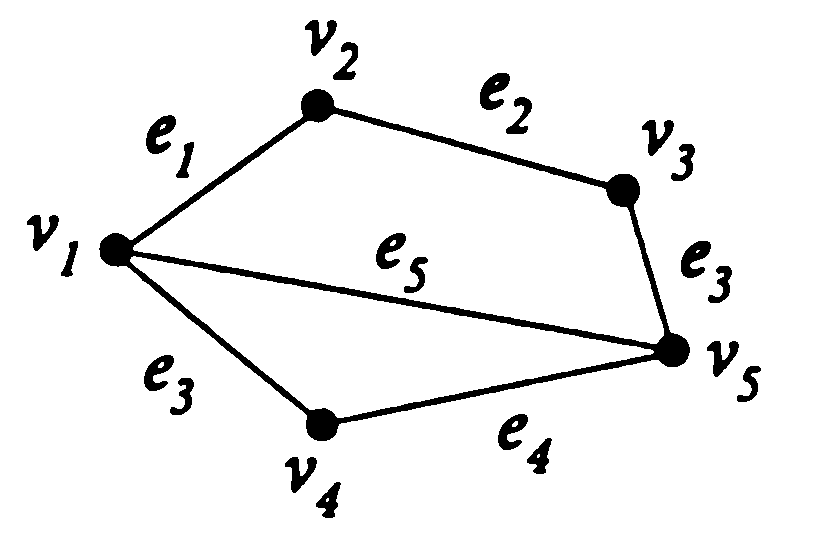 б)
б) 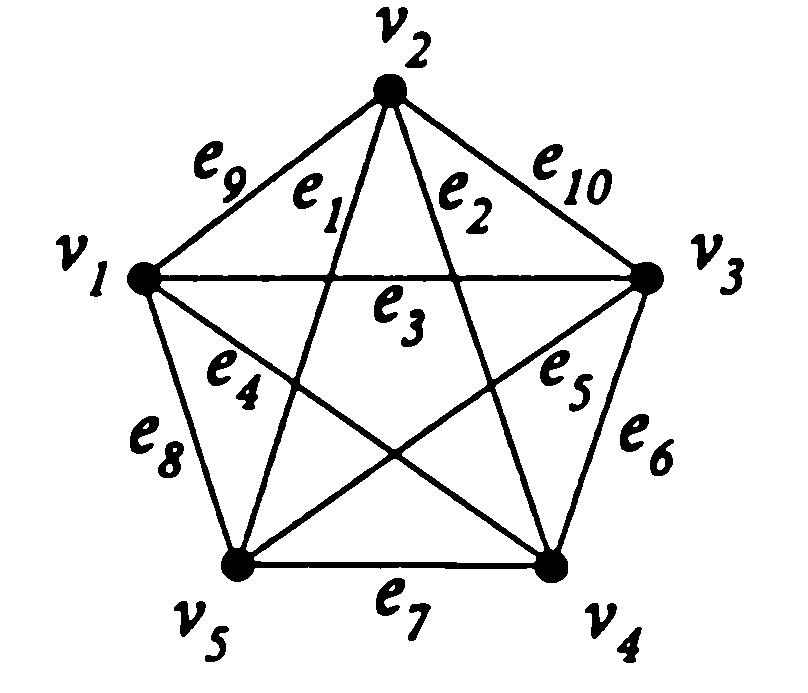 в)
в) 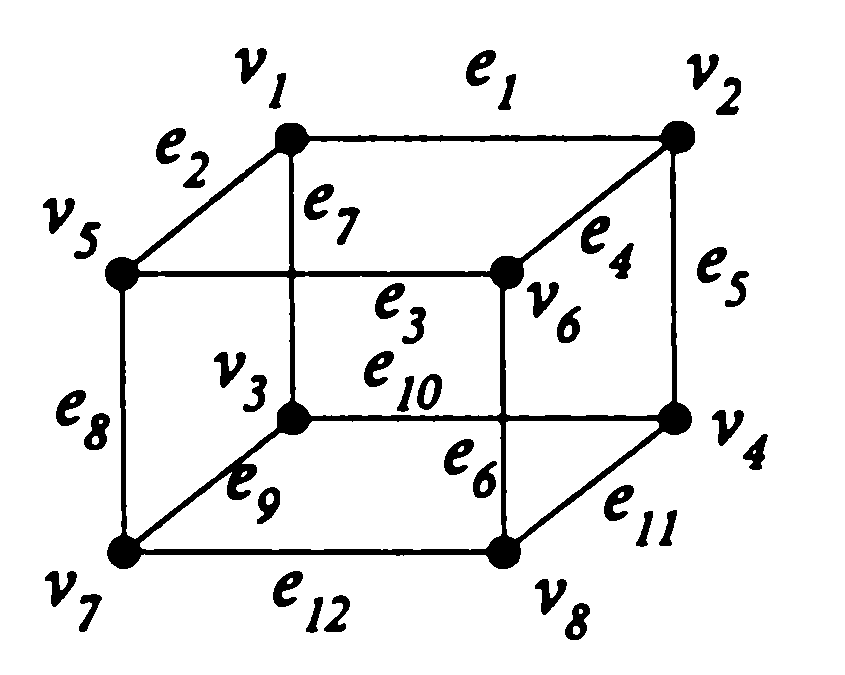
2. Найти матрицы смежности графов из первого задания.
3. Найти соответствующий граф для а) матрицы смежности; б) матрицы инцидентности
А)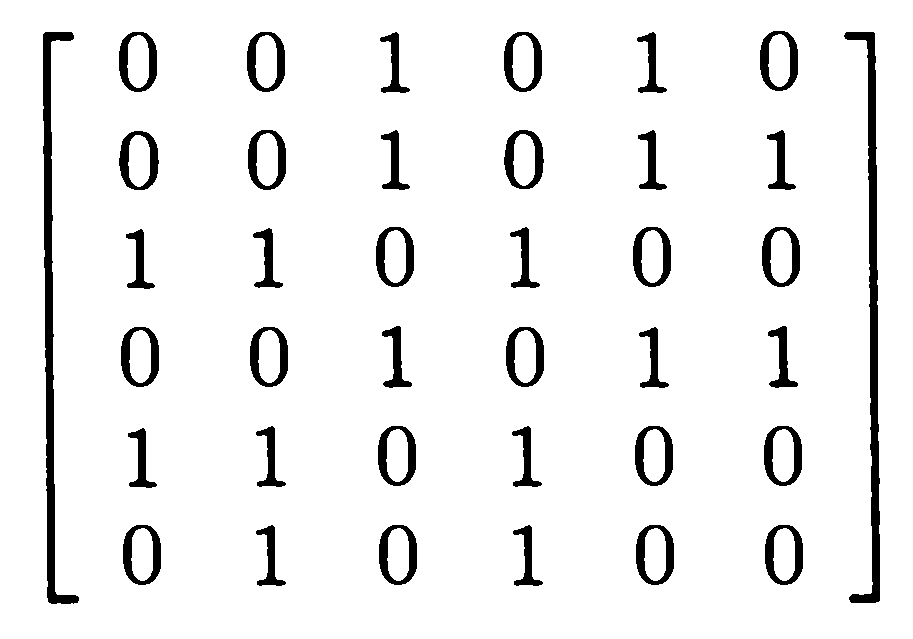 Б)
Б)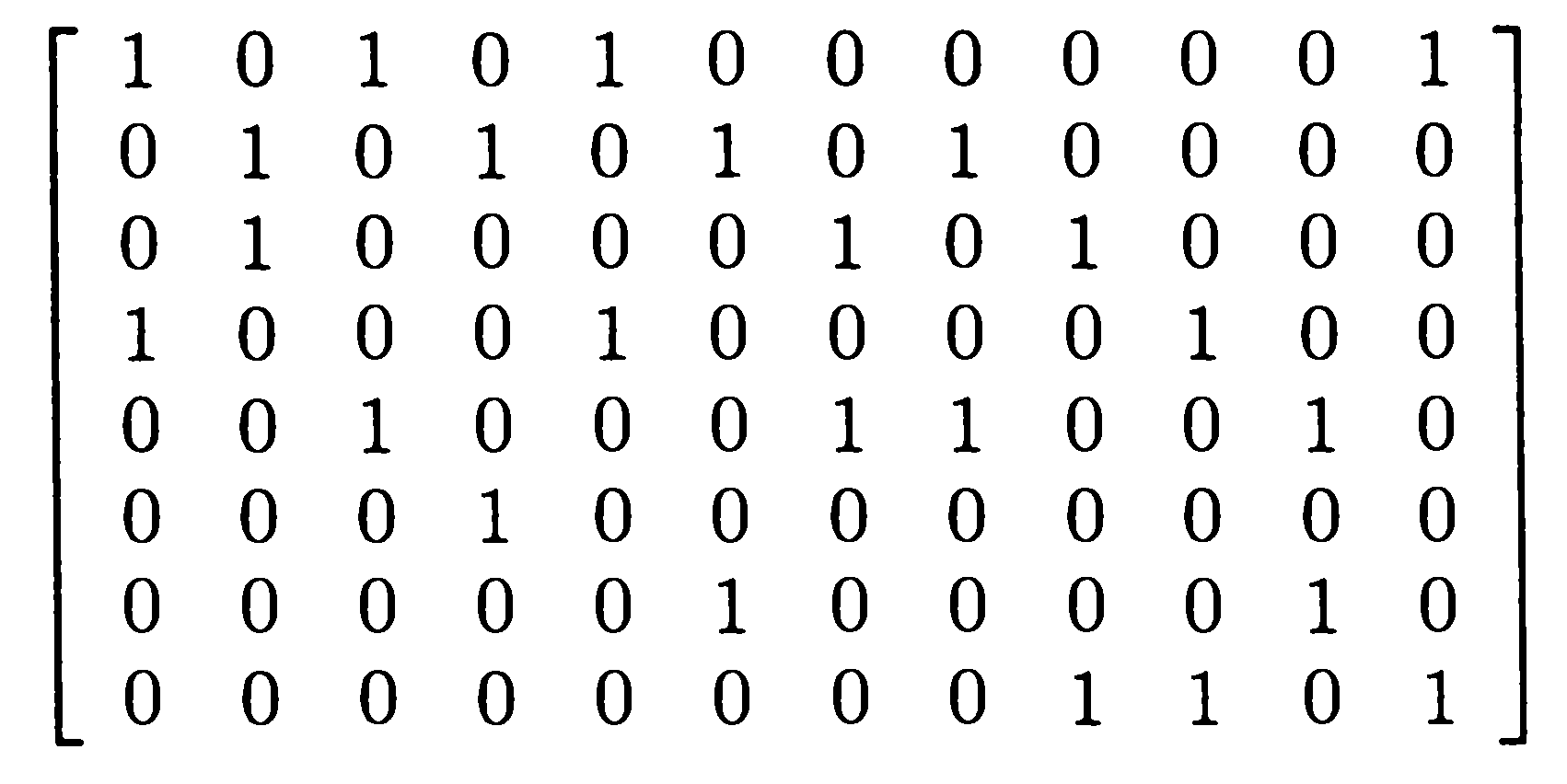
II вариант
А)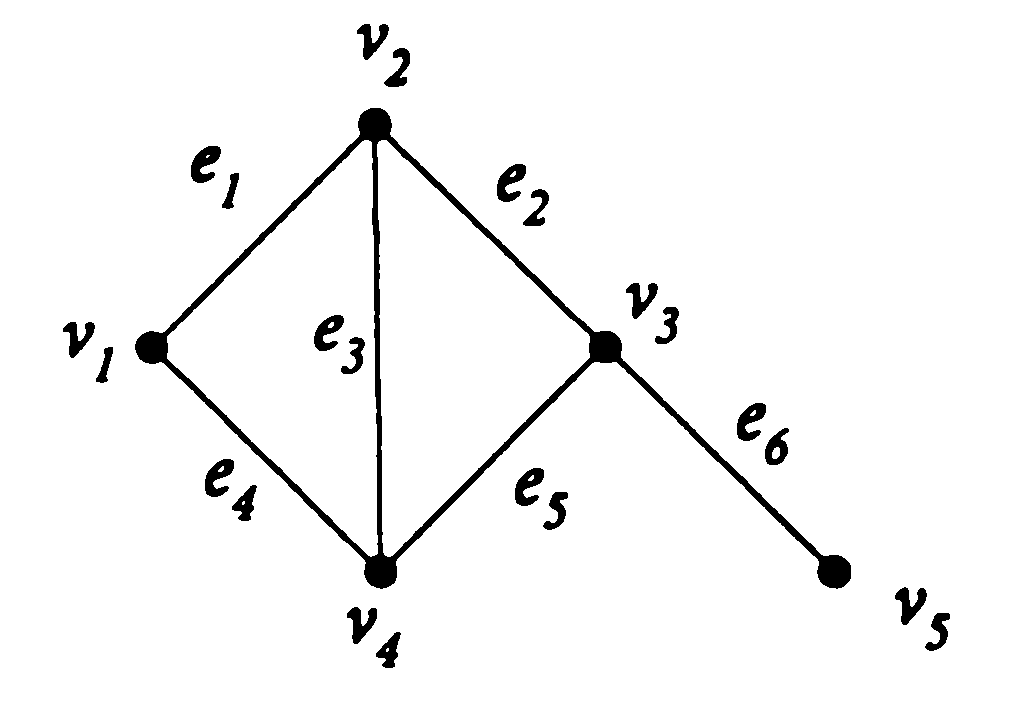 б)
б) 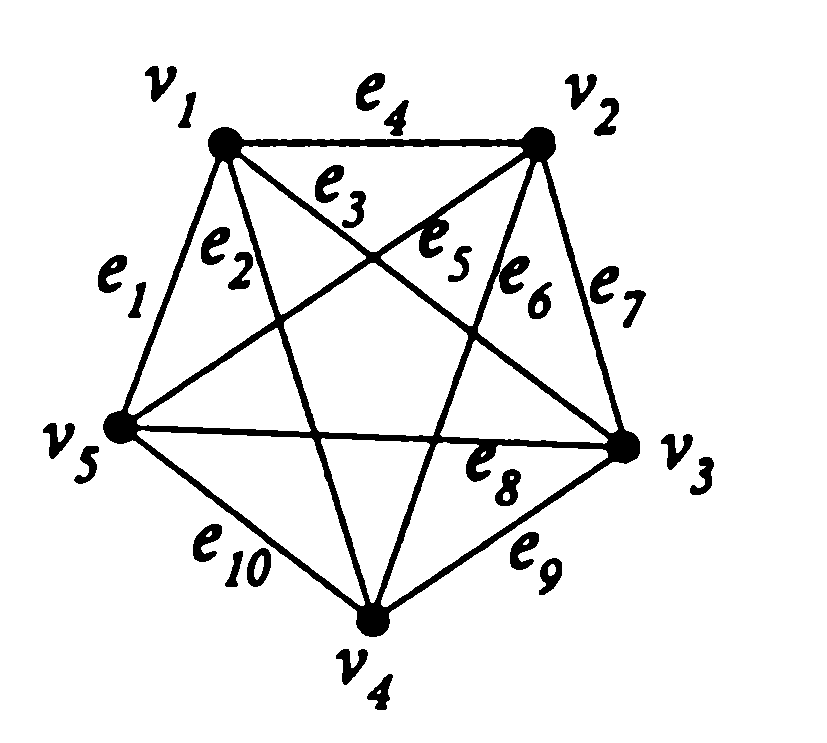 в)
в) 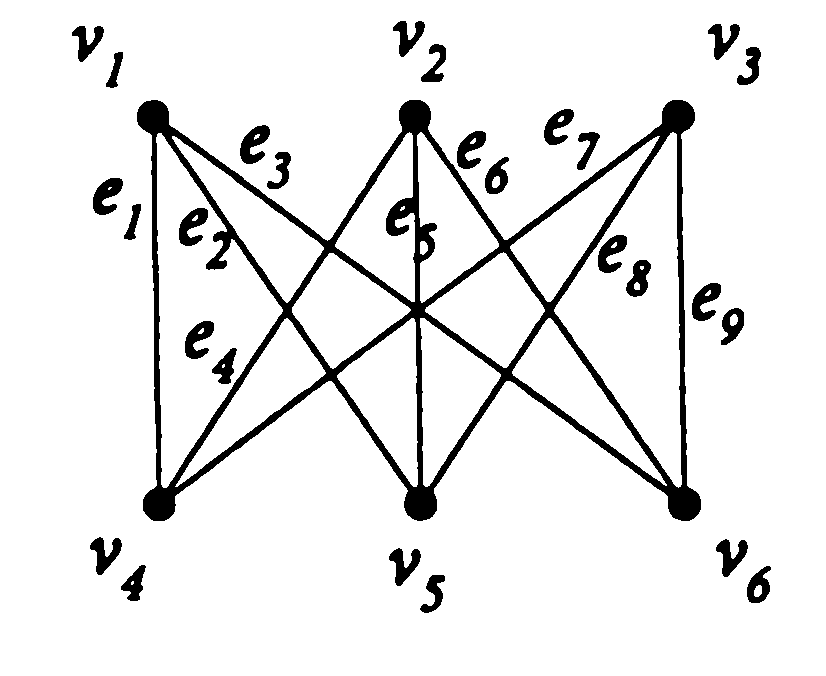
2. Найти матрицы смежности графов из первого задания.
3. . Найти соответствующий граф для а) матрицы смежности; б) матрицы инцидентности
А)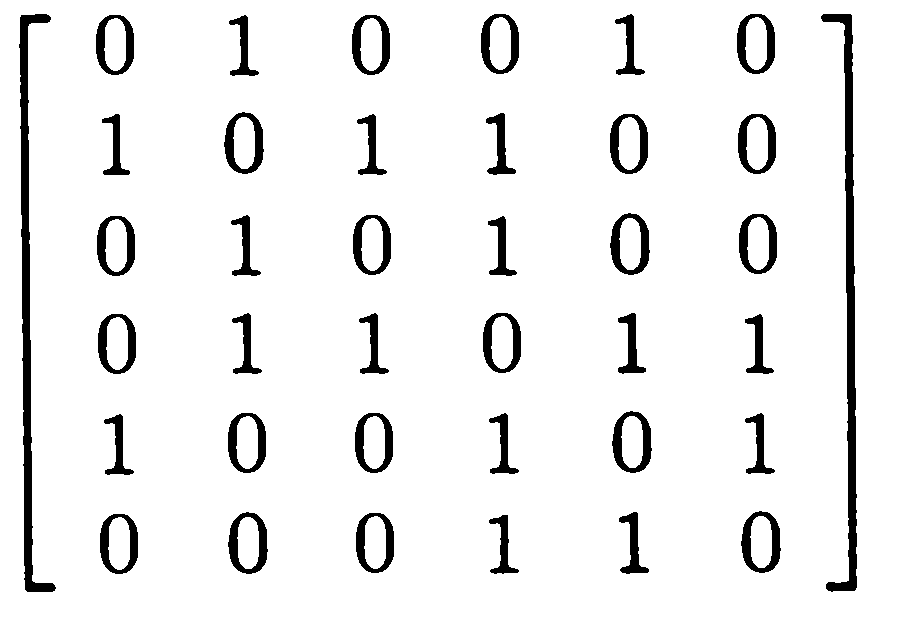 Б)
Б)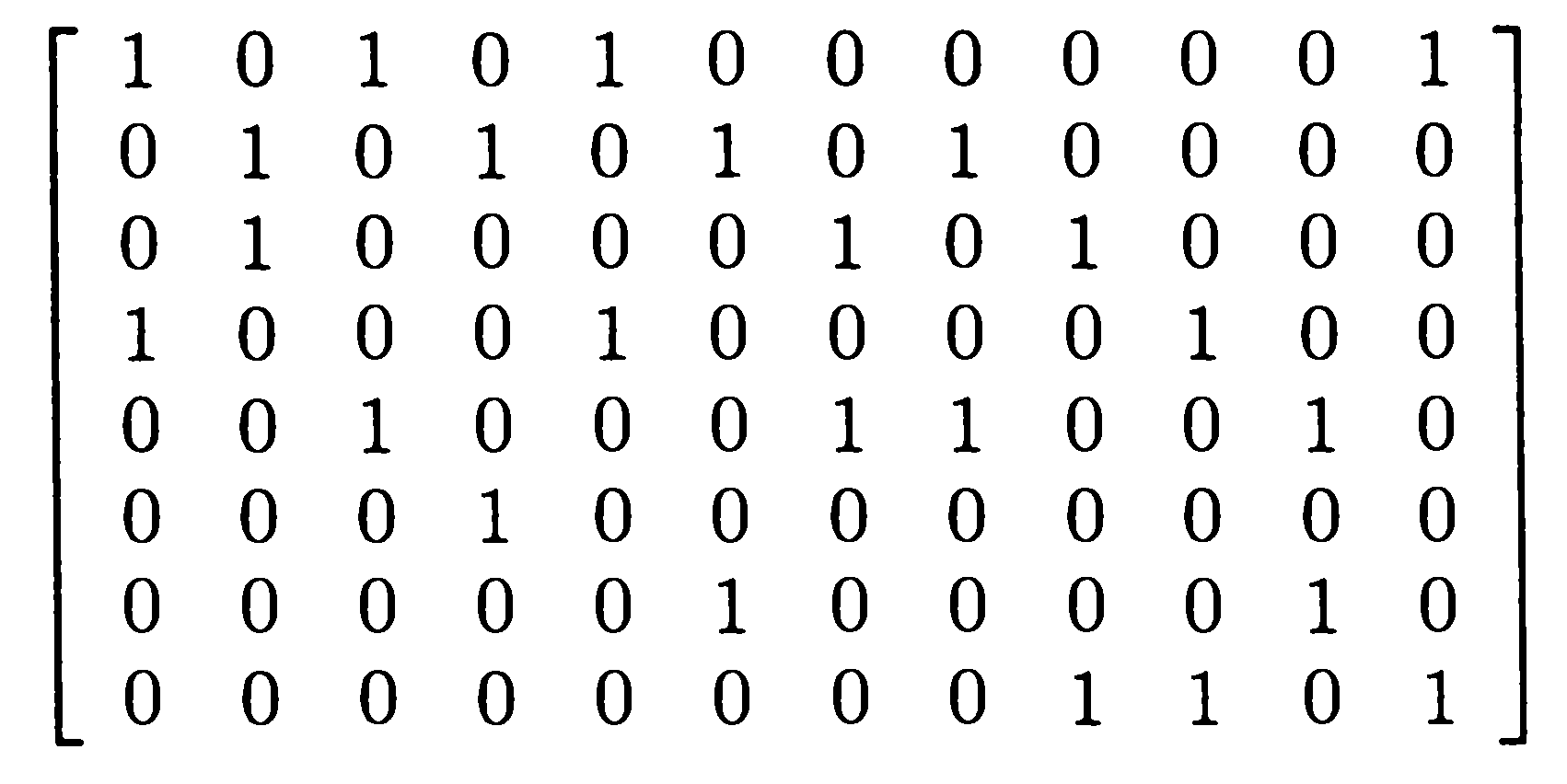
КОНТРОЛЬНЫЕ ВОПРОСЫ
ЛИТЕРАТУРА

Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.

Ответ.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 2 | 0 | 0 |
| 2 | 3 | 0 | 0 | 1 | 1 |
| 3 | 2 | 0 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Матрица инцидентности H - это матрица размера n x m, где n - число вершин графа, m - число рёбер графа. Обычно в матрице инцидентности строки соответствуют вершинам графа, а столбцы - рёбрам графа.
Матрица инцидентности для неориентированного графа
Элемент матрицы инцидентности для неориентированного графа hij определяется следующим образом:
- равен единице, если вершина vi инцидентна ребру ej;
- равен нулю, если вершина vi не инцидентна ребру ej.
Пример 3. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

Ответ.
| V | 1-2 | 1-3 | 2-4 | 2-5 | 3-5 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 |
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
I вариант
-
Найти матрицы инцидентности следующих графов.
А)
 б)
б)  в)
в) 
2. Найти матрицы смежности графов из первого задания.
3. Найти соответствующий граф для а) матрицы смежности; б) матрицы инцидентности
А)
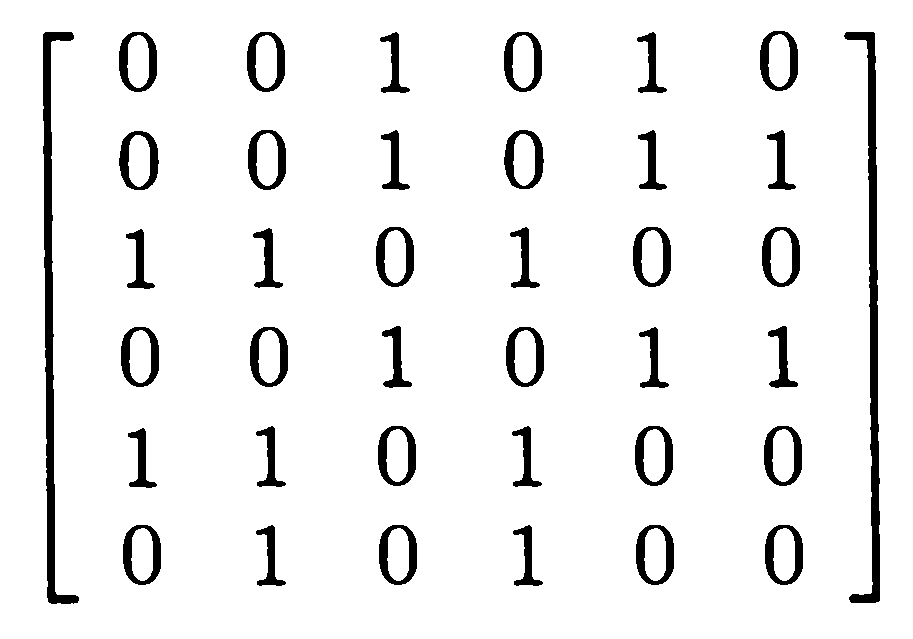 Б)
Б)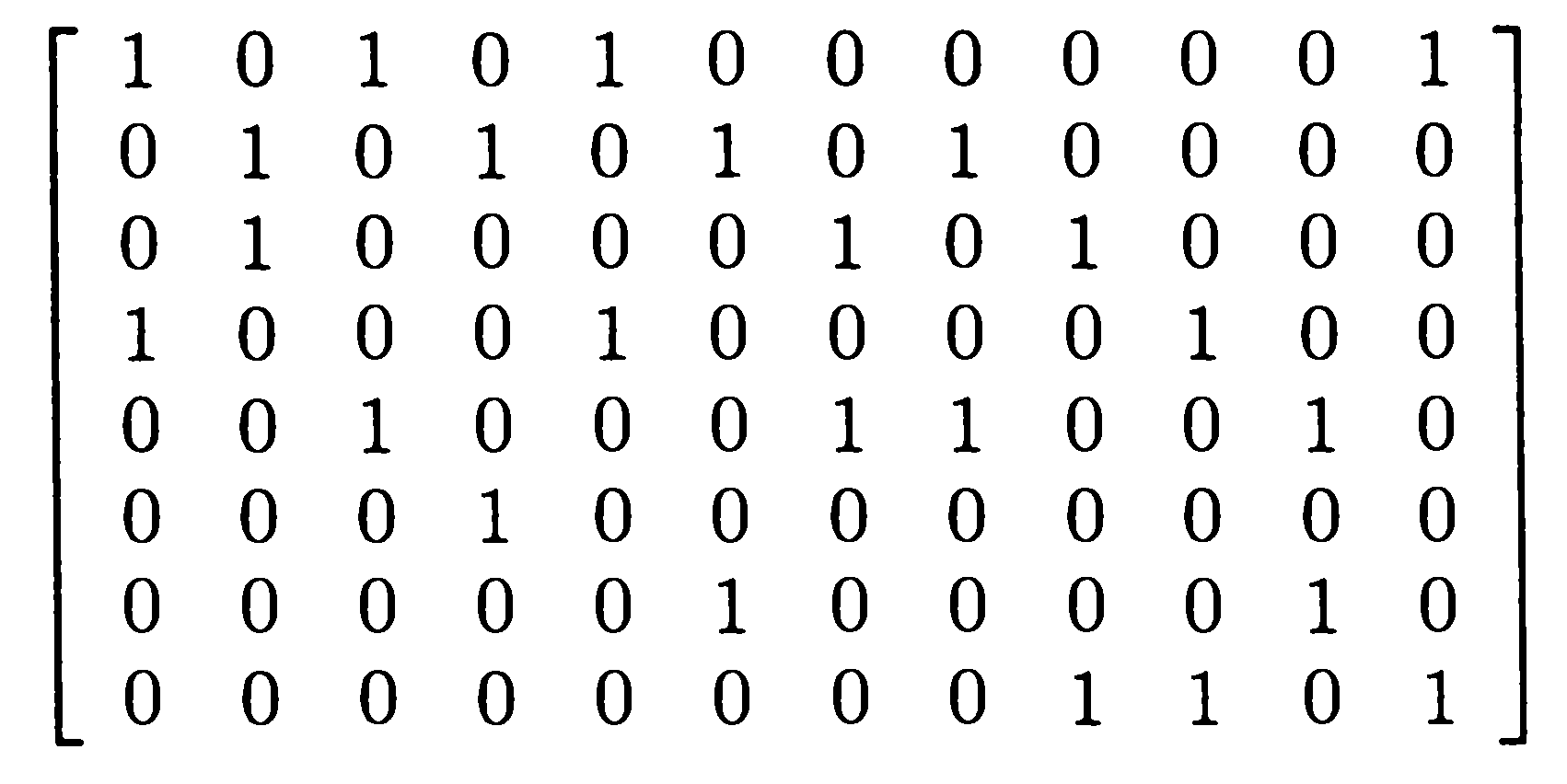
II вариант
-
Найти матрицы инцидентности следующих графов.
А)
 б)
б) 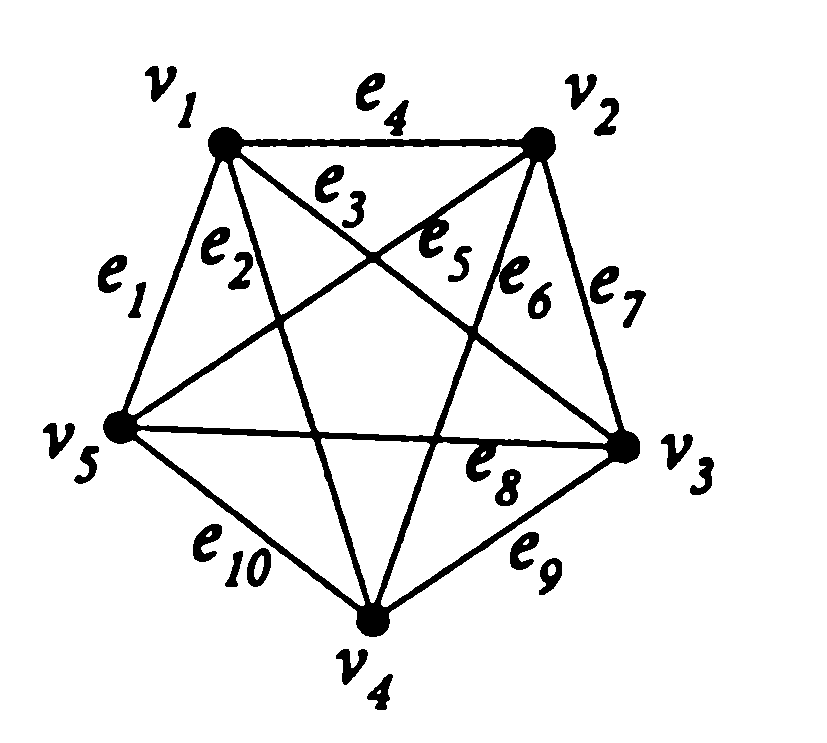 в)
в) 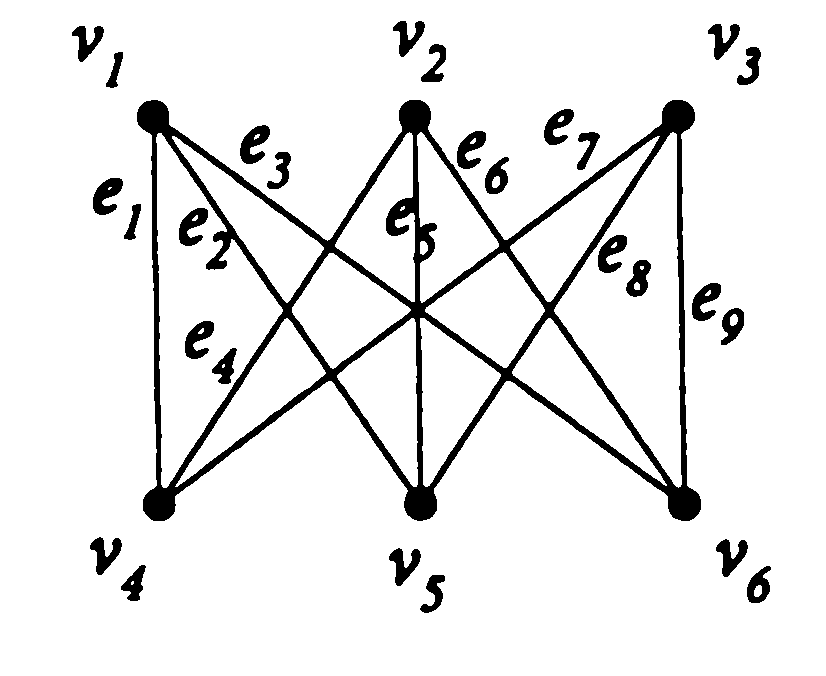
2. Найти матрицы смежности графов из первого задания.
3. . Найти соответствующий граф для а) матрицы смежности; б) матрицы инцидентности
А)
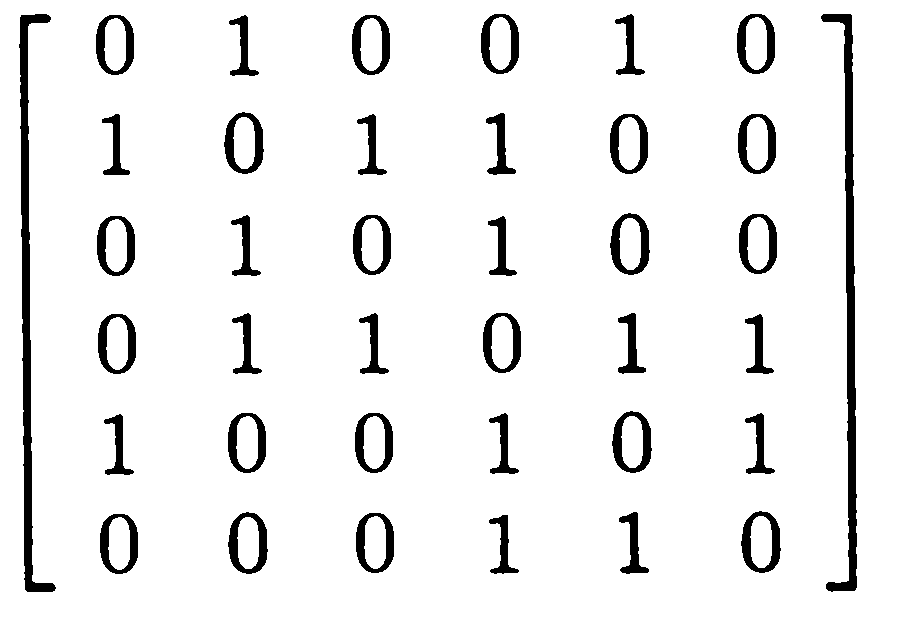 Б)
Б)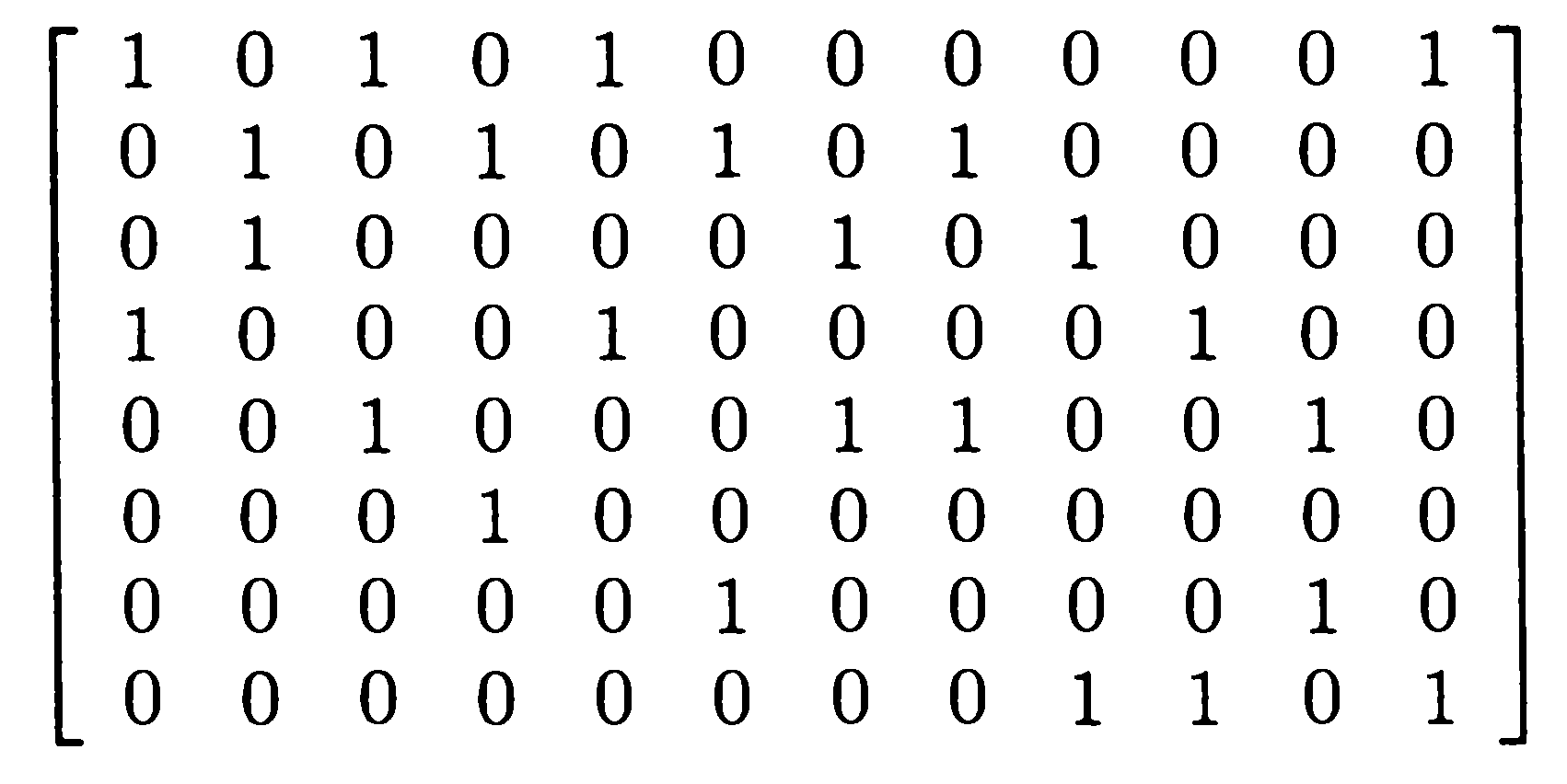
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Чем отличаются матрицы инцидентности и смежности?
ЛИТЕРАТУРА
-
Татт У. Теория графов. Пер. с англ. – М.: Мир, 2005.
