Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1002
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
10(10) = 10,7%; Р10(k<3) = 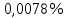 ; Р10(k≥3) = 99,99%
; Р10(k≥3) = 99,99%
Пример 4. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Дано:
n = 400; k = 104; p = 0,2; q = 0,8
Решение
Т.к. n и k велики, то используем локальную теорему Муавра-Лапласа:
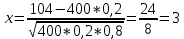 → По таблице
→ По таблице 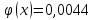
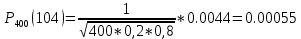
Ответ: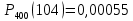
Пример 5. Вероятность повреждения товара равна 0,02. Найти вероятность того, что из ста единиц товара испортится ровно 3.
Дано:
n= 100; k = 3; p = 0,02
Решение
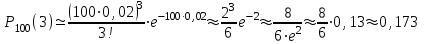
Ответ: Р100(3) = 0,173
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
I вариант
II вариант
III вариант
IV вариант
КОНТРОЛЬНЫЕ ВОПРОСЫ
Литература
Практическая работа №6
РЕШЕНИЕ ЗАДАЧ НА ПОСТРОЕНИЕ РЯДА РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И НАХОЖДЕНИЕ ЕЁ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Цель работы: научиться строить закон распределения дискретной случайной величины табличным способом, с помощью многоугольника распределения и функции распределения.
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетной документации, принимать участие в разработке проектной документации на модификацию информационной системы; ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ:90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Для задания дискретной случайной величины необходимо перечислить все возможные ее значения и указать их вероятности.
Законом распределения дискретной случайной величины называет соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически в виде функции распределения и графически с помощью многоугольника распределения.
Пример 1. Возможные значения случайной величины таковы: х1 = 2, х2 = 5, х3 = 8. Известны вероятности первых двух возможных значений: р1 = 0,4; р2 = 0,15. Найти вероятность х3.
Решение. Так как в одном испытании случайная величина принимает одно и только возможное значения, то события х1, х2, х3 образуют полную группу; следовательно сумма вероятностей этих событий равна единице: p1+ p2+ p3=1
рз = 1 – р1 – р2 = 1 – 0,4 – 0,15 = 0,45
Пример 2. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 500 и десять выигрышей по 10 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение.
р1 = 1/100 = 0,01 (количество выигрышей в 500 рублей делится на общее количество билетов);
р2 = 10/100 = 0,1 (количество выигрышей в 10 рублей делится на общее количество билетов);
р3 = 1 – (0,01 + 0,1) = 0,89.
Закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета:
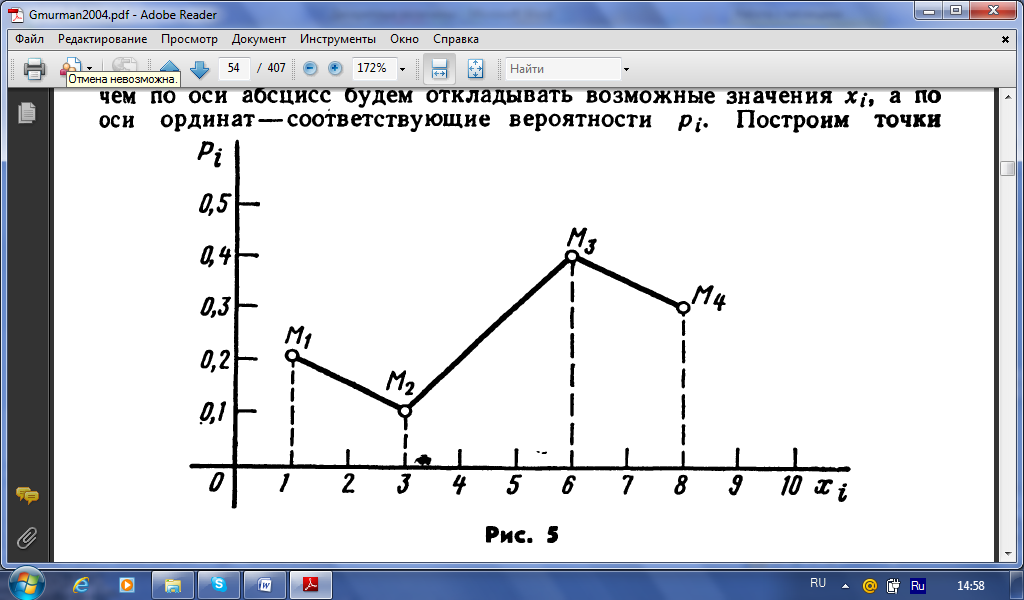
Пример 3. Дискретная случайная величина Х задана законом распределения. Построить многоугольник распределения.
Решение. Для построения многоугольника распределения в прямоугольной системе координат построим точки (хi, pi), а затем соединим их отрезками прямых.
Функция распределения случайной величины Х – это функция F(x), которая при каждом значении своего аргумента х численно равна вероятности того, что случайная величина Х кажется меньше, чем значение аргумента х: F(x) = P{X<x}
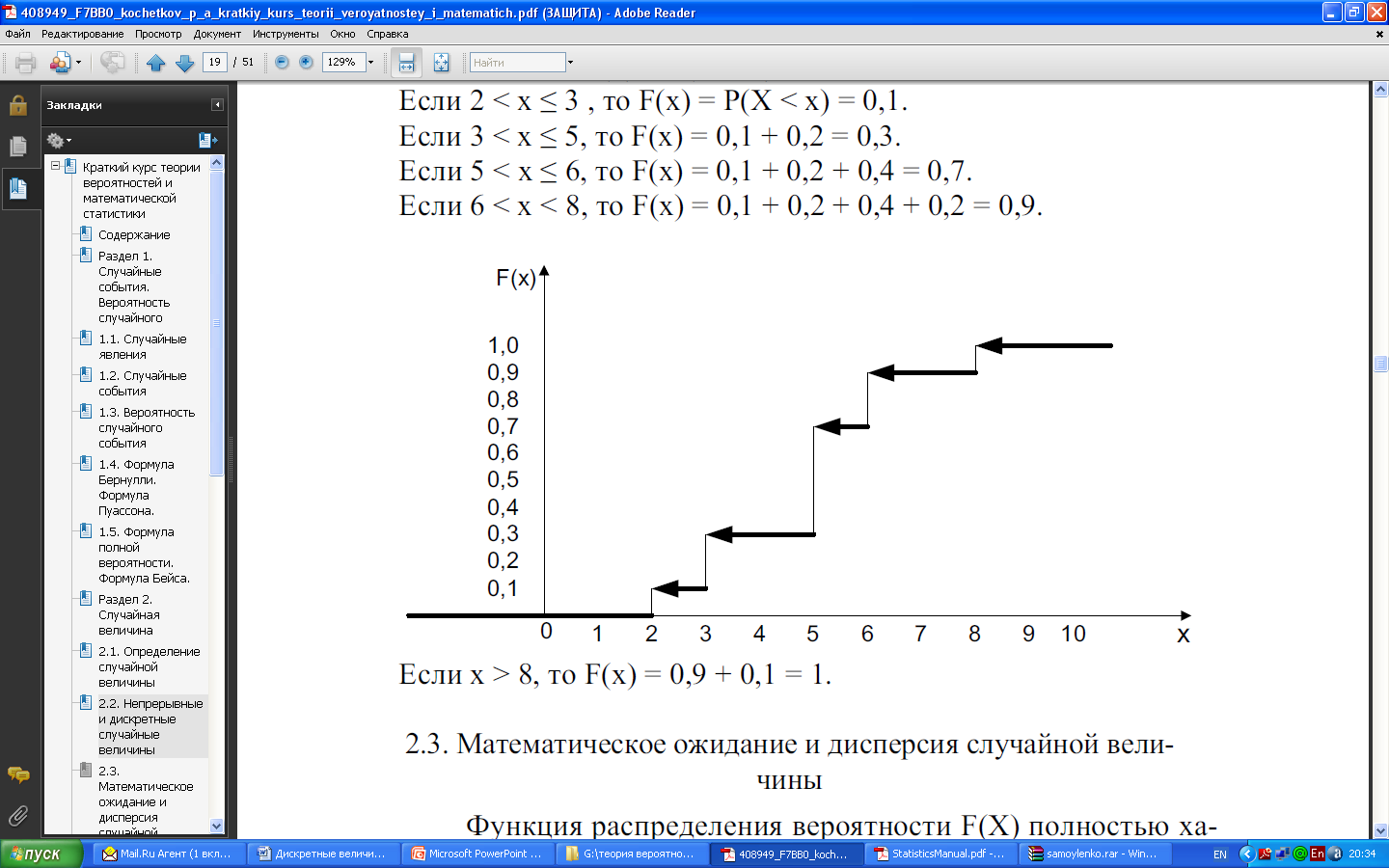
Пример 4. Дан ряд распределения дискретной случайной величины:
Построить функцию распределения этой случайной величины и ее график.
Решение
При нахождении закона распределения дискретной случайной величины часто необходимо использовать сложение и умножение вероятностей.
Пример 5. Два орудия стреляют по цели; вероятности попадания в цель при одном выстреле для них равны соответственно 0,7 и 0,8. Для случайной величины Х (числа попаданий в мишень при одном залпе) составить ряд распределения.
Решение.
Р(х2=1) = 0,7∙(1 - 0,8) + (1 – 0,7)∙0,8 = 0,14 + 0,24 = 0,38
Составляем ряд распределения.
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
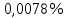 ; Р10(k≥3) = 99,99%
; Р10(k≥3) = 99,99%Пример 4. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Дано:
n = 400; k = 104; p = 0,2; q = 0,8
Решение
Т.к. n и k велики, то используем локальную теорему Муавра-Лапласа:
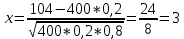 → По таблице
→ По таблице 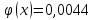
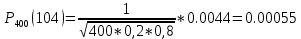
Ответ:
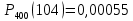
Пример 5. Вероятность повреждения товара равна 0,02. Найти вероятность того, что из ста единиц товара испортится ровно 3.
Дано:
n= 100; k = 3; p = 0,02
Решение
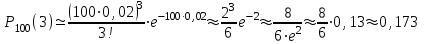
Ответ: Р100(3) = 0,173
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
I вариант
-
Устройство, состоящее из пяти независимо работающих элементов. Вероятность отказа каждого из них за сутки равна 0,2. Найти вероятность того, что откажут: а) три элементы; б) не менее 4 элементов; в) менее 4 элементов. -
По результатам ежегодной проверки Портнадзором судов, было установлено: вероятность того что суда имеют нарушения правил Морского Регистра равна 0,4. Найти вероятность того, что из 2400 судов, заходивших в порт в течение этого периода, имеют нарушения правил 960 судов. -
Пусть вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.
II вариант
-
Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) 2 телевизора потребуют ремонта; б) не более одного потребует ремонта; б) более одного потребует ремонта. -
Вероятность найти белый гриб среди прочих равна 0,25. Какова вероятность того, что среди 300 грибов белых будет 75? -
С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия.
III вариант
-
Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что: а) герб выпадет три раза; б) герб выпадет менее трех раз; в) герб выпадет во всех испытаниях. -
На заводе изготавливается в среднем 75% деталей отличного качества. За час было изготовлено 400 деталей. Найти вероятность того, что среди них ровно 280 деталей отличного качества. -
Среди шариковых авторучек в среднем при упаковке, отгрузке и доставке в магазин повреждаются 0,02%. Найти вероятность того, что среди 5000 авторучек окажутся поврежденными не более 3 ручек.
IV вариант
-
Производится залп из 5 орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,7. Найти вероятность попадания в объект: а) трех орудий; б) более трех орудий; в) менее трех орудий. -
Вероятность получения с конвейера изделия первого сорта равна 0,8. Определить вероятность того, что из взятых на проверку 400 изделий 315 будут первого сорта. -
Вероятность рождения белого тигра равна 0,02. Найти вероятность того, что среди 100 рождённых тигрят окажется 3 белых.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
При каких условиях удобнее пользоваться формулой Бернулли, при каких – формулой Лапласа, а при каких – формулой Пуассона?
Литература
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.
Практическая работа №6
РЕШЕНИЕ ЗАДАЧ НА ПОСТРОЕНИЕ РЯДА РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И НАХОЖДЕНИЕ ЕЁ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Цель работы: научиться строить закон распределения дискретной случайной величины табличным способом, с помощью многоугольника распределения и функции распределения.
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетной документации, принимать участие в разработке проектной документации на модификацию информационной системы; ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ:90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Для задания дискретной случайной величины необходимо перечислить все возможные ее значения и указать их вероятности.
Законом распределения дискретной случайной величины называет соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически в виде функции распределения и графически с помощью многоугольника распределения.
Пример 1. Возможные значения случайной величины таковы: х1 = 2, х2 = 5, х3 = 8. Известны вероятности первых двух возможных значений: р1 = 0,4; р2 = 0,15. Найти вероятность х3.
Решение. Так как в одном испытании случайная величина принимает одно и только возможное значения, то события х1, х2, х3 образуют полную группу; следовательно сумма вероятностей этих событий равна единице: p1+ p2+ p3=1
рз = 1 – р1 – р2 = 1 – 0,4 – 0,15 = 0,45
Пример 2. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 500 и десять выигрышей по 10 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение.
-
Возможные значения выигрыша: х1 = 500, х2 = 10, х3 = 0. -
Вероятности возможных значений:
р1 = 1/100 = 0,01 (количество выигрышей в 500 рублей делится на общее количество билетов);
р2 = 10/100 = 0,1 (количество выигрышей в 10 рублей делится на общее количество билетов);
р3 = 1 – (0,01 + 0,1) = 0,89.
Закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета:
| Х | 500 | 10 | 0 |
| р | 0,01 | 0,1 | 0,89 |
Пример 3. Дискретная случайная величина Х задана законом распределения. Построить многоугольник распределения.
| Х | 1 | 3 | 6 | 8 |
| Р | 0,2 | 0,1 | 0,4 | 0,3 |
Решение. Для построения многоугольника распределения в прямоугольной системе координат построим точки (хi, pi), а затем соединим их отрезками прямых.

Функция распределения случайной величины Х – это функция F(x), которая при каждом значении своего аргумента х численно равна вероятности того, что случайная величина Х кажется меньше, чем значение аргумента х: F(x) = P{X<x}
Пример 4. Дан ряд распределения дискретной случайной величины:
| Х | 2 | 3 | 5 | 6 | 8 |
| р | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Построить функцию распределения этой случайной величины и ее график.
Решение
-
Если значение аргумента x≤2, то F(x) = P (X -
Если значение аргумента 2 -
Если значение аргумента 3 -
Если значение аргумента 5 -
Если значение аргумента 6 -
Если значение аргумента x>8, то F(x) = P (X

При нахождении закона распределения дискретной случайной величины часто необходимо использовать сложение и умножение вероятностей.
Пример 5. Два орудия стреляют по цели; вероятности попадания в цель при одном выстреле для них равны соответственно 0,7 и 0,8. Для случайной величины Х (числа попаданий в мишень при одном залпе) составить ряд распределения.
Решение.
-
Возможные значения случайной величины: х1 = 0, х2 = 1, х3 = 2. -
Вероятности возможных значений:-
х1=0, если оба орудия не попали в цель Р(х1=0) = (1-0,7)(1-0,8)= 0,06. -
х2=1, если в цель попало ровно 1 орудие
-
Р(х2=1) = 0,7∙(1 - 0,8) + (1 – 0,7)∙0,8 = 0,14 + 0,24 = 0,38
-
х2=2, если оба орудия попали в цель Р(Х=2)= 0,7⋅0,8 = 0,56.
Составляем ряд распределения.
| Х | 0 | 1 | 2 |
| р | 0,06 | 0,38 | 0,56 |
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
| | I вариант | II вариант | ||||||||||||||||||||||||
| 1. | Возможные значения случайной величины таковы: х1 = 6, х2 = 7, х3 = 8. Известны вероятности первых двух возможных значений: р2 = 0,6; р3 = 0,25. Найти вероятность х1. | Возможные значения случайной величины таковы: х1 = 1, х2 = 2, х3 = 3. Известны вероятности первых двух возможных значений: р1 = 0,45; р3 = 0,3. Найти вероятность х2. | ||||||||||||||||||||||||
| 2. | Дискретная случайная величина Х задана законом распределения. Построить многоугольник распределения.
| Дискретная случайная величина Х задана законом распределения. Построить многоугольник распределения.
| ||||||||||||||||||||||||
| 3. | В лотерее среди 100 билетов 5 с выигрышем 1000 руб., 15 – 100 руб., 25 – 10 руб., остальные по 0. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета. | В лотерее разыгрывается 1000 билетов. Среди них два выигрыша по 50 руб., пять по 20 руб., десять по 10 руб., 25 по 5 руб. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета. | ||||||||||||||||||||||||
| 4. | Два стрелка произвели по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5; вторым - 0,4. Составить закон распределения числа попаданий в мишень. | Два стрелка произвели по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,7; вторым - 0,6. Составить закон распределения числа попаданий в мишень. | ||||||||||||||||||||||||
| 5. | Дан ряд распределения дискретной случайной величины:
Построить функцию распределения этой случайной величины и ее график. | Дан ряд распределения дискретной случайной величины:
Построить функцию распределения этой случайной величины и ее график. | ||||||||||||||||||||||||
| 6. | Телефонистка трижды вызывает абонента. Вероятность того, что будет принят первый вызов, равна 0,2, второй вызов – 0,3 и третий вызов – 0,4. Составить закон распределения вероятностей числа X вызовов, принятых абонентом. | Составить закон распределения вероятностей числа Х исправных приборов, если их три, а вероятности того, что исправны, соответственно равны 0,9, 0,8, 0,7. |