Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1005
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
По выборке объема n = 41 найдена смещенная оценка Dв = 3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
ЛИТЕРАТУРА
-
Спирина М. С., Спирин П.А. Теория вероятностей и математическая статистика: учебник для студентов учреждений среднего профессионального образования – М.: «Академия», 2012. – 352 с. -
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие. – М.: Высшая школа, 2007. – 400 с.
Практическая работа №14
ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ И ВЕРОЯТНОСТИ СОБЫТИЯ
ЦЕЛЬ РАБОТЫ: научиться оценивать математическое ожидание генеральной дисперсии.
Для выполнения работы необходимо знать виды числовых характеристик выборок и формулы для их определения, интервальные оценки; необходимо уметь определять числовые характеристики выборок и интервальные оценки.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Интервальной называют оценку, которая определяется двумя числами — концами интервала. Доверительный интервал – это интервал, в который с заданной вероятностью попадет неизвестное значение оцениваемого параметра распределения.
Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии имеет следующий смысл: с надежностью γ можно утверждать, что доверительный интервал (
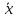
– tσ/
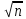 ,
,  + tσ/
+ tσ/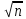 ) покрывает неизвестный параметр а; точность оценки δ = tσ/
) покрывает неизвестный параметр а; точность оценки δ = tσ/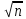 .
. P(
 – tσ/
– tσ/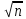 < a <
< a <  + tσ/
+ tσ/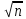 ) = 2Ф(t) = γ
) = 2Ф(t) = γДоверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии имеет следующий вид:
P(
 – tγ*s/
– tγ*s/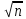 < a <
< a <  + tγ*s/
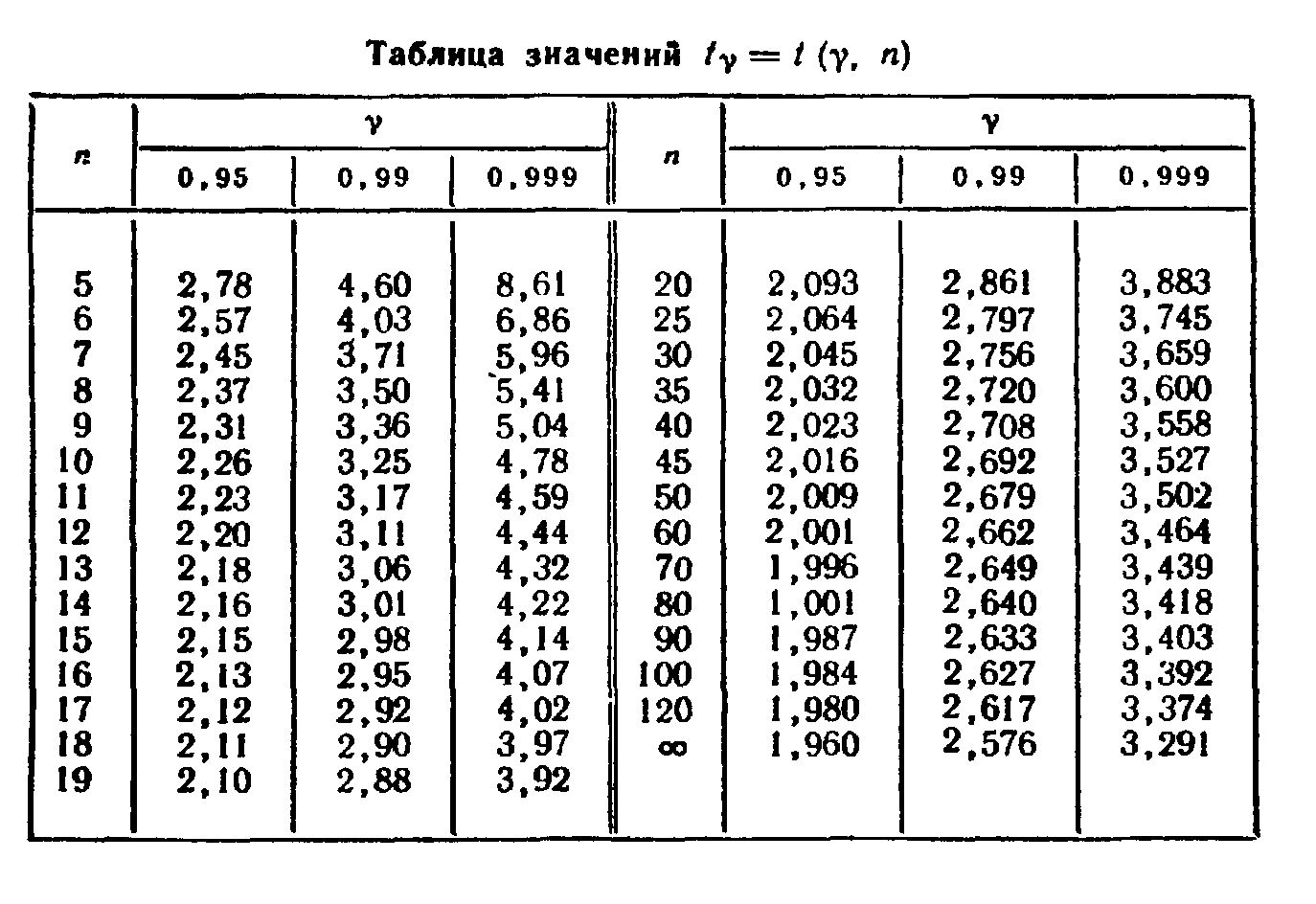
+ tγ*s/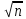 ) = γ, где s - «исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице приложения по заданным n и γ.
) = γ, где s - «исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице приложения по заданным n и γ.Пример 1. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением σ = 3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним
 , если объем выборки n = 36 и задана надежность оценки γ = 0,95.
, если объем выборки n = 36 и задана надежность оценки γ = 0,95. Решение
Найдем t. Из соотношения 2Ф(t) = 0,95 получим Ф(t) = 0,475. По таблице приложения 2 находим t = l,96.
Найдем точность оценки: δ = tσ/
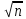 = 1.96*3/
= 1.96*3/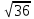 = 0,98
= 0,98Получим доверительный интервал: (
 – 0,98;
– 0,98; 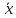 + 0,98).
+ 0,98). Пример. 2 Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 16 найдены выборочная средняя
 = 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.
= 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.
Решение
Найдем tγ. Пользуясь таблицей приложения при γ = 0,95 и n = 16, получим tγ = 2,13.
Найдем доверительные границы:
 – tγ*s/
– tγ*s/ =20,2 – 2,13*0,8/
=20,2 – 2,13*0,8/ 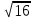 = 19,774.
= 19,774.  + tγ*s/
+ tγ*s/ =20,2 +2,13*0,8/
=20,2 +2,13*0,8/ 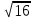 = 20,626.
= 20,626. Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774 < а < 20,626.
Интервальной оценкой (с надежностью γ) неизвестной вероятности р биномиального распределения по относительной частоте w служит доверительный интервал: P1 < Р < Р2.
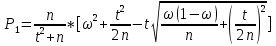
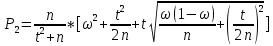
где n – общее число испытаний; m – число появлений события; w – относительная частота, равная отношению m/n; t – значение аргумента функции Лапласа, при котором Ф(t)= γ/2 (у – заданная надежность).
Пример 1. Производят независимые испытания с одинаковой, но неизвестной вероятностью Р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности Р с надежностью 0,95, если в 80 испытаниях событие А появилось 16 раз.
Решение. По условию, n = 80, m=16, γ = 0,95. Найдем относительную частоту появления события А:
w = m/n = 16/80 = 0,2.
Найдем t из соотношения Ф (t) = γ/2 = 0,95/2 =0,475; по таблице функции Лапласа находим t = 1,96.
Подставив n = 80, w = 0,2, t = 1,96 в формулы для p1 и p2, получим соответственно р1= 0,128, р2 =0,299.
Искомый доверительный интервал 0,128< р< 0,299.
При больших значениях n (порядка сотен) в качестве приближенных границ доверительного интервала можно принять выражения:
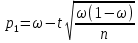 ,
, 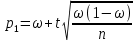
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
I вариант
-
Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной совокупности, если генеральное среднее квадратическое отклонение σ = 5, выборочная средняя = 14 и объем выборки n = 25.
= 14 и объем выборки n = 25. -
По данным девяти независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений = 30,1 и «исправленное» среднее квадратическое отклонение s = 6. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью γ = 0,99. Предполагается, что результаты измерений распределены нормально.
= 30,1 и «исправленное» среднее квадратическое отклонение s = 6. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью γ = 0,99. Предполагается, что результаты измерений распределены нормально. -
Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000ч. Найти с надёжностью 0,95 доверительный интервал для средней продолжительности а горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы 40ч. -
Производятся независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью 0,95, если в 60 испытаниях событие А появилось 15 раз. -
Изготовлен экспериментальный игровой автомат, который должен обеспечить появление выигрыша в одном случае из 100 бросаний монеты в автомат. Для проверки пригодности автомата произведено 400 испытаний, причем выигрыш появился 5 раз. Найти доверительный интервал, покрывающий неизвестную вероятность появления выигрыша с надежностью Y = 0,999.
II вариант
-
Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания а нормально распределенного признака X генеральной совокупности, если известны генеральное среднее квадратическое отклонение σ = 4, выборочная средняя = 10,2 и объем выборки n = 16.
= 10,2 и объем выборки n = 16. -
По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений = 42,8 и «исправленное» среднее квадратическое отклонение s = 1. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью γ = 0,95. Предполагается, что результаты измерений распределены нормально.
= 42,8 и «исправленное» среднее квадратическое отклонение s = 1. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью γ = 0,95. Предполагается, что результаты измерений распределены нормально. -
Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений 40м произведено 5 равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния а до цели с надёжностью 0,95, зная среднее арифметическое результатов измерений 2000м. -
Производятся независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью 0,99, если в 100 испытаниях событие А появилось 60 раз. -
Произведено 300 испытаний, в каждом из которых неизвестная вероятность р появления события А постоянна. Событие А появилось в 250 испытаниях. Найти доверительный интервал, покрывающий неизвестную вероятность р с надежностью 0,95.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Что такое доверительный интервал? -
Какая зависимость является корреляционной?
ЛИТЕРАТУРА
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.
Практическая работа №15
ПОСТРОЕНИЕ ВЫБОРОЧНОГО УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ РЕГРЕССИИ.
Цель работы: научиться строить выборочное уравнение прямой линии регрессии методом наименьших квадратов.
Для выполнения работы необходимо знать основы корреляционного анализа; необходимо уметь определять выборочное уравнение прямой линии регрессии.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Выборочное уравнение прямой линии регрессии Y на Х имеет вид: y = ρx + b,
где
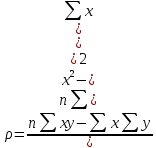 – выборочный коэффициент регрессии Y на Х
– выборочный коэффициент регрессии Y на Х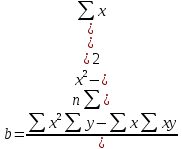 – свободный член
– свободный членПример 1. Найти выборочное уравнение прямой линии регрессии Y на Х по данным пяти наблюдений:
| Х | 1.0 | 1.5 | 3.0 | 4.5 | 5.0 |
| Y | 1.25 | 1.4 | 1.5 | 1.75 | 2.25 |
Решение
-
Составим расчетную таблицу:
| х | y | x2 | xy |
| 1 | 1.25 | 1.0 | 1.25 |
| 1.5 | 1.4 | 2.25 | 2.1 |
| 3.0 | 1.5 | 9.0 | 4.5 |
| 4.5 | 1.75 | 20.25 | 7.875 |
| 5.0 | 2.25 | 25.0 | 11.25 |
| Σx = 15 | Σy = 8.15 | Σx2 = 57.5 | Σxy = 26.975 |