Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 1004

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.




  1. Найдем выборочный коэффициент регрессии и свободный член:





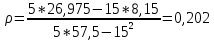
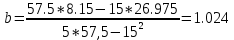
  1. Получаем уравнение регрессии: Y = 0.202x +1.024


ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
I вариант

  1. Найти выборочное уравнение прямой линии регрессии по данным n=8 наблюдений, которые получены при изучении зависимости количества продаж товара у от затрат на рекламу этого товара х:

х
1,5
4,0
5,0
7,0
8,5
10,0
11,0
12,5
12,8
13,2

y
5,0
4,5
7,0
6,5
9,5
9,0
11,0
9,0
9,8
11,2


Построить график по результатам измерений, на этом же графике построить найденное выборочное уравнение прямой линии регрессии.

  1. Реализовать задачу 1 в программе Microsoft Excel.


II вариант

  1. Исследование зависимости между среднемесячными доходами X на семью (в тыс. у.е.) и расходами Y на покупку кондитерских изделий (в у.е.) представлено в таблице:

X
4,8
3,8
5,4
4,2
3,4
4,6
3,4
4,8
5,0
3,8

Y
75
68
78
71
64
73
66
75
75
65

Найти выборочное уравнение прямой линии регрессии.

Построить график по результатам измерений, на этом же графике построить найденное выборочное уравнение прямой линии регрессии.

  1. Реализовать задачу 1 в программе Microsoft Excel.

КОНТРОЛЬНЫЕ ВОПРОСЫ



  1. Какая зависимость является корреляционной?


ЛИТЕРАТУРА


  1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.

Практическая работа №16

ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК НЕОРИЕНТИРОВАННЫХ ГРАФОВ. РЕШЕНИЕ ЗАДАЧ С ПРИМЕНЕНИЕМ ГРАФОВ
ЦЕЛЬ РАБОТЫ: научиться определять основные характеристики графов и решать задачи с их применением.
Для выполнения работы необходимо знать основные понятия теории графов; необходимо уметь: определять характеристики графов, осуществлять операции над графами, определять вид графа, решать задачи с применением графов.

Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности.
ВРЕМЯ ВЫПОЛНЕНИЯ:90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Графом G = (V, E) называется множество V – множество вершин и Е – множество ребер. Если у ребер не указано направление, то такой граф называется неориентированным, у ориентированного графа каждое ребро имеет направление.

Степенью вершины графа deg(V) называется количество ребер ей инцидентных.

Путем в графе называется последовательность ребер, по которым можно двигаться по графу, причем каждое ребро должно встречать не более одного раза.

Простым путем называется путь, в котором нет повторяющихся вершин.

Циклом называется путь, соединяющий вершину саму с собой и не содержащий повторяющихся ребер. В простом цикле не содержится повторяющихся вершин.

Операции над графами:

  1. Объединение графов включает все вершины и ребра, которые содержатся в исходных графах.

  2. Пересечение графов включает только одинаковые вершины и ребра, которые содержатся в исходных графах.

  3. Кольцевая сумма содержит объединение графов без их пересечения.

  4. Дополнение содержит те вершины и ребра, которые не хватает исходному до полного графа.

Эйлеровым графом называется граф, содержащий эйлеров цикл (цикл, содержащий все ребра графа только один раз).


Гамильтоновым графом называется граф, содержащий гамильтонов цикл (цикл, проходящий через каждую вершину только один раз).
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
Задание 1. Имеется граф G = (V, E) , где V = {1, 2, 3, 4, 5, 6}, E = {(1,2), (1,3), (1,4), (3,2), (3,5), (3,6), (4,6)}.

а) Изобразите графически в виде неориентированного графов.

б) Определите степень каждой вершины неориентированного графа

Задание 2. Имеется граф с множеством вершин {1, 2, 3, 4, 5, 6, 7}; ниже в таблице для каждой вершины перечислены смежные с ней вершины:

1
2
3
4
5
6
7

4, 5, 7
3, 6
2, 4, 5, 7
1, 3
1, 3, 6
5, 2, 7
1, 3, 6

а) изобразить графически в виде неориентированного графа;

б) привести пример простого пути в этом графе;

в) цикла в этом графе, не являющегося простым циклом

г) простого цикла в этом графе.
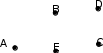
З 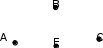адание 3. Даны два графа G1 = (V1, E1) и G2 = (V2, E2)
Изобразите геометрически объединение графов 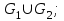пересечение графов 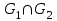и кольцевую сумму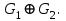
Задание 4. Изобразите дополнения графов:


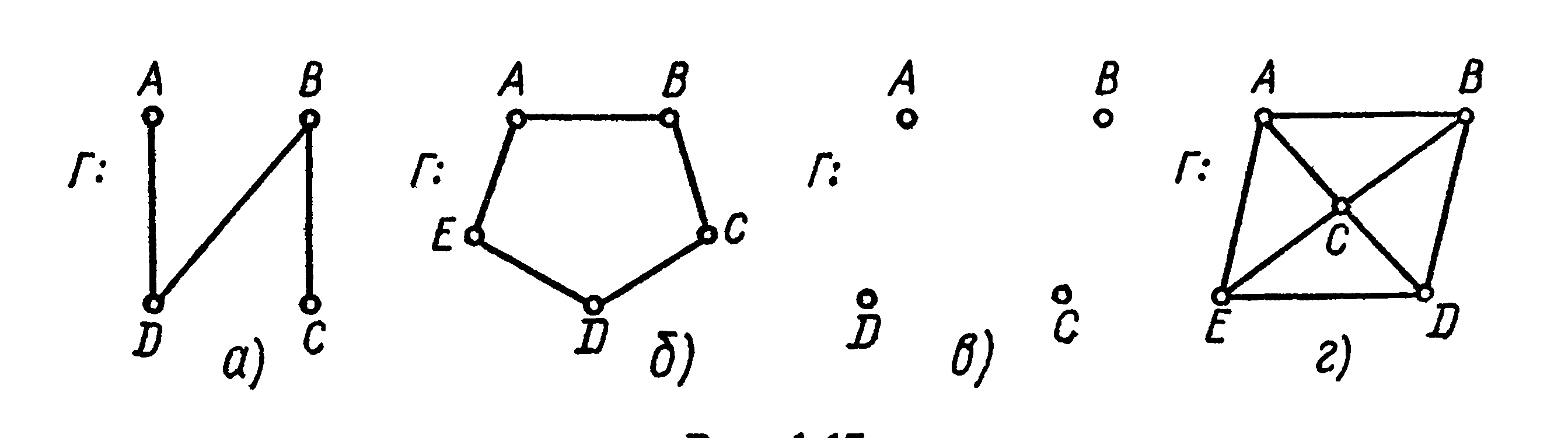
Здание 5. Какой граф, представленный на рисунке является эйлеровым или гамильтоновым?



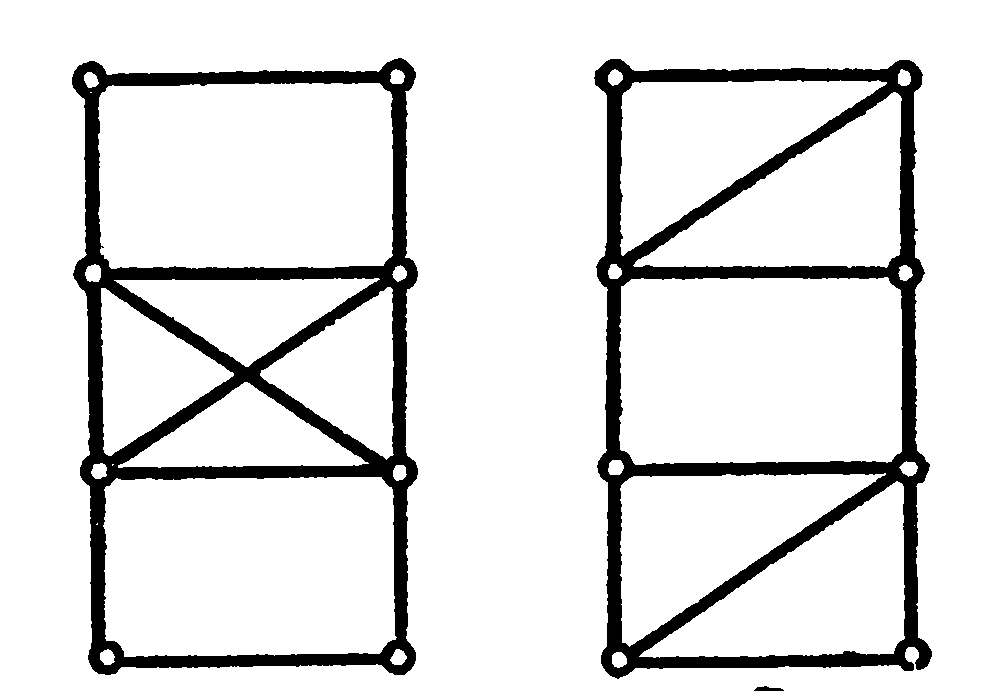
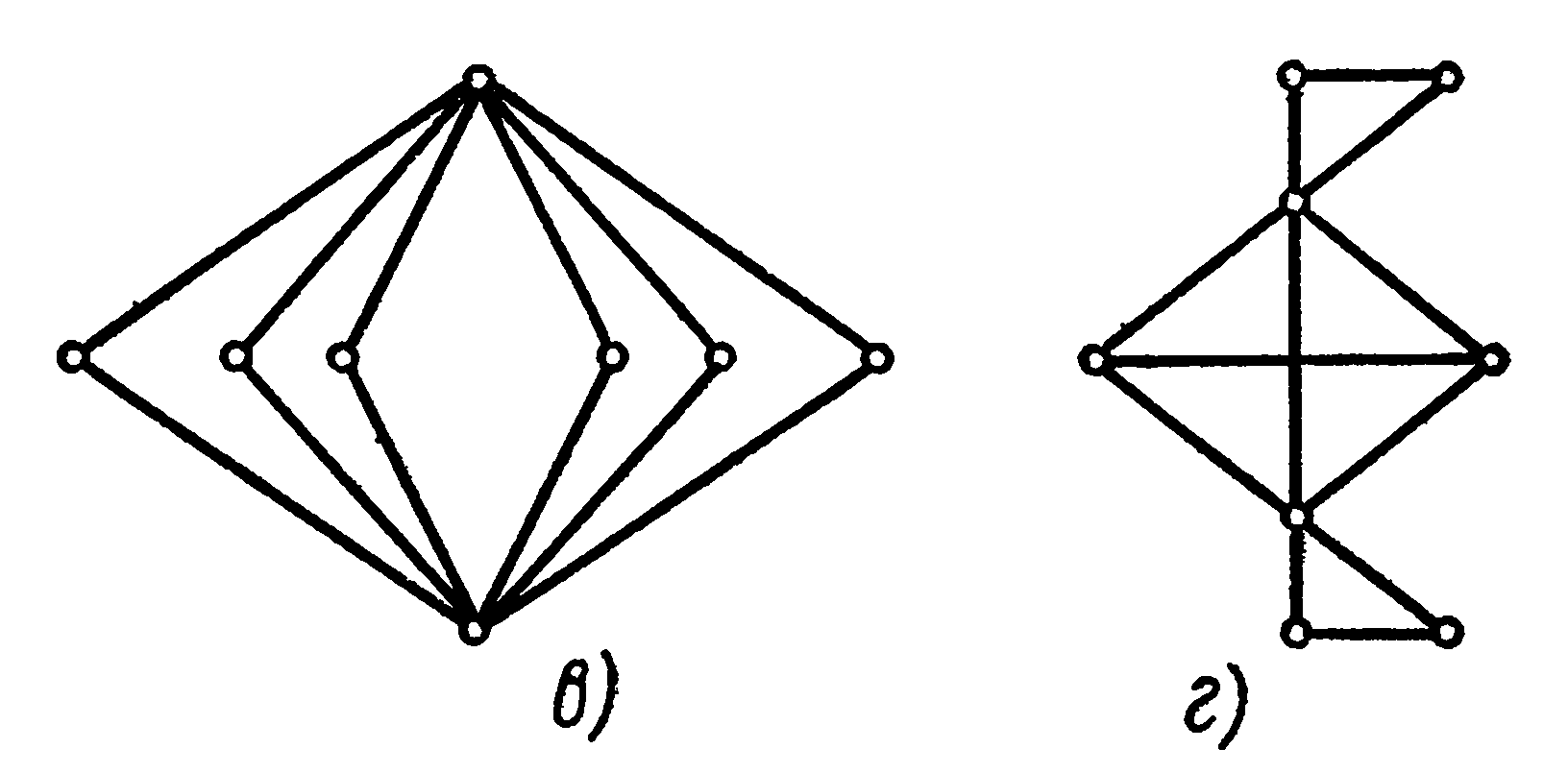
Задание 6. Из пункта А в пункт В выехали пять машин одной марки разного цвета: белая, чёрная, красная, синяя, зелёная. Чёрная едет впереди синей, зелёная – впереди белой, но позади синей, красная впереди чёрной. Какая машина едет первой и какая последней?

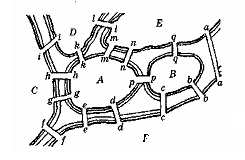
Задание 7. В некоторой местности через протоки переброшено 15 мостов. Изобразите схему с помощью графа, где вершины – это участки суши, а ребра – мосты. Можно ли обойти все мосты, проходя по каждому из них только один раз? Докажите это теоретически, если можно, то укажите такой путь. Какой тип графа вы получили?


КОНТРОЛЬНЫЕ ВОПРОСЫ


  1. Какие существуют виды графов? Охарактеризуйте каждый вид.

  2. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что: Вода и молоко не в бутылке. Сосуд с лимонадом стоит между кувшином и сосудом с квасом. В банке не лимонад и не вода. Стакан стоит между банкой и сосудом с молоком. В каком сосуде находится, какая из жидкостей?


ЛИТЕРАТУРА


  1. Татт У. Теория графов. Пер. с англ. – М.: Мир, 2005.


Практическая работа № 17

НАХОЖДЕНИЕ МАТРИЦ ИНЦИДЕНТНОСТИ И СМЕЖНОСТИ ГРАФОВ
ЦЕЛЬ РАБОТЫ: научиться определять матрицы инцидентности и смежности графов.
Для выполнения работы необходимо знать основные понятия теории графов; необходимо уметь: решать задачи с применением графов.

Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности.

ВРЕМЯ ВЫПОЛНЕНИЯ:90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Графы можно представить в аналитической форме либо матрицей смежности, либо матрицей инцидентности.
Матрица смежности S - это квадратная матрица, в которой число строк и число столбцов равно n - числу вершин графа. В ячейки матрицы смежности записываются некоторые числа в зависимости от того, соединены соответствующие вершины рёбрами или нет, и от типа графа.
Элемент матрицы смежности sij неориентированного графа определяется следующим образом:

- равен единице, если вершины vi и vj смежны;

- равен нулю, если вершины vi и vj не смежны.

Если для элемента матрицы vij имеет место i = j, то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.
Пример 1. Составить матрицу смежности для графа, представленного на рисунке ниже.



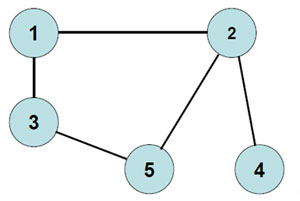
Ответ.

V
1
2
3
4
5

1
0
1
1
0
0

2
1
0
0
1
1

3
1
0
0
0
1

4
0
1
0
0
0

5
0
1
1
0
0


Матрица смежности неориентированного графа симметрична относительно главной диагонали.
Если в графе есть вершины, соединённые между собой несколькими рёбрами, то элемент матрицы смежности sij равен числу рёбер, соединяющих вершины v

Смотрите также файлы