Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1000
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Министерство образования Нижегородской области |
| Государственное бюджетное профессиональное образовательное учреждение Арзамасский коммерческо-технический техникум |
| |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ РАБОТ
Теория вероятностей и математическая статистика
Специальность: 09.02.04 Информационные системы (по отраслям)
2017 г
| Одобрена методическим объединением информационных дисциплин Протокол №___ от «___»_____________20 г Председатель МО: _________________Н.Ю. Куликова | Составлена в соответствии с требованиями к результатам освоения основной профессиональной образовательной программы специальности 09.02.04 Информационные системы (по отраслям) Зам. директора по УиНМР __________________ М.А. Ледянкина |
| | |
.
Автор: Н.Г. Саблукова, к.п.н., преподаватель специальных дисциплин высшей квалификационной категории ГБПОУ «Арзамасский коммерческо-технический техникум»
Методические указания содержат задания к практическим работам, порядок их выполнения, рекомендации, перечень контрольных вопросов по каждой практической работе, требования к знаниям и умениям. Приведен список основной литературы, рекомендуемой для подготовки к практическим работам.
Методические указания предназначены для студентов специальности 09.02.04 Информационные системы (по отраслям).

С
 ОДЕРЖАНИЕ
ОДЕРЖАНИЕ| Введение | 4 |
| Практическая работа №1 Решение задач на расчёт количества выборок. | 5 |
| Практическая работа №2 Вычисление вероятностей событий по классической формуле определения вероятности. | 7 |
| Практическая работа №3 Вычисление вероятностей сложных событий с помощью теорем умножения и сложения вероятностей. | 9 |
| Практическая работа №4 Вычисление вероятностей сложных событий с помощью формулы полной вероятности и формулы Байеса. | 11 |
| Практическая работа №5 Вычисление вероятностей событий в схеме Бернулли. | 13 |
| Практическая работа №6 Решение задач на запись распределения дискретной случайной величины. | 16 |
| Практическая работа №7 Вычисление характеристик дискретной случайной величины и характеристик функций от дискретной случайной величины. | 19 |
| Практическая работа №8 Решение задач на запись биноминального и геометрического распределений. | 22 |
| Практическая работа №9 Решение задач на формулу геометрического определения вероятности. | 25 |
| Практическая работа №10 Вычисление вероятностей и нахождение характеристик для непрерывной случайной величины с помощью функции плотности и интегральной функции распределения. | 28 |
| Практическая работа №11 Вычисление вероятностей для нормально и показательно распределенных величин. | 32 |
| Практическая работа №12 Построение для заданной выборки ее графической диаграммы; расчёт по заданной выборке её числовых характеристик. | 35 |
| Практическая работа №13 Интервальное оценивание математического ожидания нормального распределения. | 39 |
| Практическая работа №14 Интервальное оценивание вероятности события. | 42 |
| Практическая работа №15 Моделирование случайных величин; моделирование случайной точки, равномерно распределённой в прямоугольнике; моделирование сложных испытаний и их результатов. | 43 |
Введение
Методические указания к практическим работам по дисциплине «Теория вероятностей и математическая статистика» предназначены для обучающихся по специальности 09.02.04 Информационные системы (по отраслям).
Учебная дисциплина «Теория вероятностей и математическая статистика» входит в математический и общий естественнонаучный цикл и направлена на формирование базового уровня знаний, необходимых для освоения общепрофессиональных дисциплин и профессиональных модулей. Включенные в практические работы задачи стимулируют исследовательскую и творческую деятельность, развивает познавательные интересы, помогают не только глубже понять математику, но и научиться применять полученные знания на практике.
Целью выполнения практических работ по данной дисциплине является формирования у обучающихся навыков владения математическим аппаратом теории вероятности и математической статистики для решения прикладных задач. Методические указания к практическим работам содержат тему, цель, теоретические сведения, методические указания по решению задач и задания на выполнения.
Каждая практическая работа оформляется в тетрадях для практических работ. В оформление работы входить запись номера практической работы, темы, цели, задания с решением и выводы. На выполнение практической работы отводится 1 пара.
Практическая работа № 1
РЕШЕНИЕ ЗАДАЧ НА РАСЧЁТ КОЛИЧЕСТВА ВЫБОРОК
ЦЕЛЬ РАБОТЫ: научиться определять тип комбинаторного объекта и рассчитывать количество выборок заданного типа
Для выполнения работы необходимо знать: основные комбинаторные объекты (типы выборок), формулы и правила расчёта количества выборок; необходимо уметь: определять тип комбинаторного объекта (тип выборки), рассчитывать количество выборок заданного типа в заданных условиях.
Выполнение данной практической работы способствует формированию профессиональной компетенции ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Комбинаторика – это раздел математики, в котором изучается, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.
Все комбинаторные формулы можно вывести из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения. Эти два важных правила часто применяются при решении комбинаторных задач.
Основными понятиями комбинаторики являются размещения, перестановки и сочетания.
-
Размещением из n элементов по m называется любое упорядоченное подмножество, состоящее из m различных элементов данного множества.
-
Число размещений (без повторений) из n элементов по m элементам равно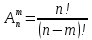
Пример 1. Сколькими способами можно выбрать председателя, заместителя и профорга из 9 человек?
Решение. n = 9, m = 3.
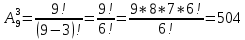
-
Число размещений (с повторением) из n элементов по m равно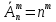 .
.
Пример 2. Сколькими способами можно рассадить 7 человек по 9 вагонам?
Решение. Так как в один вагон могут сесть несколько человек, и рассадка зависит от того кто в каком вагоне находится, то используем формулу размещения с повторениями:
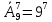
-
Перестановкой из n элементов называется размещение из n элементов по n элементам.
-
Число перестановок n различных элементов (без повторений) равно Рn=n!
Пример 3. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределиться места по окончании соревнований?
Решение. Используем формулу перестановки без повторения для n = 6:
Р6=6! = 1*2*3*4*5*6 = 720
-
Число перестановок (с повторениями) равно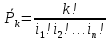
Пример 4. Сколько перестановок можно получить из букв слова КОЛОКОЛА?
Решение. Так как буквы в слове повторяются, то используем формулу перестановок с повторениями.
i1 = 2 (количество букв «к»)
i2 = 3 (количество букв «о»)
i3 = 2 (количество букв «л»)
i4 = 1 (количество букв «а»)
k = i1 + i2 + i3+ i4 = 2+3+2+1 = 8
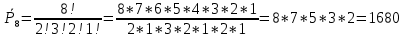
-
Сочетанием из n элементов по mназывается любое подмножество, состоящее из m различных элементов данного множества
-
Число сочетаний из n элементов по m(без повторений) равно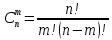
Пример 5. Из учащихся 25 человек нужно выбрать троих дежурных. Сколькими способами это можно сделать?
Решение. n = 25, m = 3.
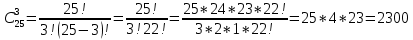
-
Число сочетаний с повторениями равно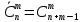
Пример 6. Сколькими способами можно купить 6 пирожных, если имеются 2 сорта пирожных по 5 в каждом?
Решение. Поскольку при покупке пирожных порядок их расположения не важен, то используем для подсчета формулу сочетаний с повторениями, при этом n = 5 +5 =10, m = 6.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
| | I вариант | II вариант |
| 1. | Сколькими способами могут восемь человек стать в очередь к театральной кассе? | Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов может он выбрать? |
| 2. | Сколько различных перестановок можно образовать из всех букв слова «Абракадабра»? | Сколько различных перестановок можно образовать из всех букв слова «Тарантас»? |
| 3. | Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов? | Сколькими способами можно выбрать 4 краски из имеющихся 9 различных красок? |
| 4. | Сколько четырехбуквенных слов можно образовать из букв слова «Сапфир»? | Сколько трехбуквенных слов можно составить из букв слова «Фонарь»? |
| 5. | Имеется 10 различных книг и 15 различных журналов. Сколькими способами можно составить посылку из 3 книг и 5 журналов? | На первой полке стоит 12 книг, а на второй 10. Сколькими способами можно выбрать 4 книги с первой полки и 3 со второй? |
| 6. | Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? | Сколько четырехзначных чисел можно составить из цифр 3, 4, 5, 6, 7, 8, 9. |
| 7. | Сколькими способами можно составить набор из 5 шоколадок, если имеются шоколадки трех сортов? | Сколькими способами можно составить коллекцию из 6 марок, если имеются марки четырех видов? |
| 8 | Имеется 10 билетов денежной лотереи и 12 билетов спортлото. Сколькими способами можно выбрать по два билета либо из первой, либо из второй лотереи? | Сколькими способами можно группу из 13 человек разбить на две подгруппы, в одной из которых должно быть не более четырех, а во второй – не более десяти человек? |
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Охарактеризуйте основные комбинаторные объекты. -
Составьте схему для определения типа комбинаторного объекта.
Литература
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с. -
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2007.
Дополнительное задание*
-
В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся? -
Сколько существует четырёхзначных пин-кодов?
Практическая работа № 2
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СОБЫТИЙ ПО КЛАССИЧЕСКОЙ ФОРМУЛЕ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ
ЦЕЛЬ РАБОТЫ: научиться вычислять вероятность события по классической формуле определения вероятности с использованием формул комбинаторики.
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Согласно классическому определению вероятности вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события А определяется формулой:
Р(А) = m/n,
где m – число элементарных исходов, благоприятствующих А;
n – число всех возможных элементарных исходов испытания.
Пример 1. В ящике имеется 10 красных и 8 синих шаров. Наудачу вынимают один шар. Найти вероятность того, что извлеченный шар окажется синим.
Решение.
| Дано: m= 7 n = 10+8 = 18 | Решение А – извлеченный шар синего цвета P(A) = m/n = 7/18 = 0,38 = 38,9% |
| Р(А) - ? | Ответ: P(A) = 38,9% |
Пример 2. Бросаются два игральных кубика. Какова вероятность, что сумма выпавших очков равна 5.
Решение.
| Дано: k = 6 – количество граней кубика. | Решение А – сумма выпавших очков на двух кубиках равна 5. P(A) = m/n Событию Aблагоприятствуют следующие исходы: (1,4), (4,1), (2,3), (3,2) → m= 4 Каждый из кубиков можно бросить шестью способами. Тогда два кубика по правилу умножения могут упасть 6*6 = 36 способами → n= 36 P(A) = 4/36 = 1/9 = 0,11 = 11% |
| Р(А) - ? | Ответ: P(A) = 11% |
Пример 3. В мешочке имеется 6 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, р, ф, а, ь, н.Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиках можно будет прочесть слово «фонарь».
Решение.
| Дано: о, р, ф, а, ь, н | Решение А – из кубиков сложилось слово «фонарь». P(A) = m/n Т.к. из данных букв слово «фонарь» можно сложить только одним способом, то событию Aблагоприятствует 1 исход. → m= 1. Количество всех возможных способов выпадения букв на кубиках равно количеству перестановок. n= P6 = 6! = 1*2*3*4*5*6 = 720 P(A) = 1/720 = 0,00139 = 1,4% |
| Р(А) - ? | Ответ: P(A) = 1,4% |
Пример 4.В группе 25 студентов. Из них 12 юношей и 13 девушек. Известно, что к доске должны быть вызваны двое учащихся. Какова вероятность, что это юноши?
Решение.
| Дано: K = 12 L = 13 H = 25 | Решение А – к доске вызваны два юноши. P(A) = m/n Число всех исходов равно количеству способов, которыми можно выбрать двух учащихся из 25 (причем порядок вызова к доске не важен) → n = 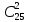 =300 =300Число благоприятствующих исходов равно числу способов выбора двух юношей из 13 → m= 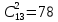 . .P(A) = 78/300=13/50 = 0,26 =26% |
| Р(А) - ? | Ответ: P(A) = 26% |
Для решения задач следующего типа:
В партии из N деталей имеется п стандартных. Наудачу отобраны т деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
можно использовать формулу:
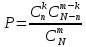
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
| | I вариант | II вариант |
| 1. | В коробке лежат 6 красных и 4 синих карандаша. Наугад вытаскиваются один из них. Найти вероятности событий того, что извлеченный карандаш красного цвета. | В коробке лежат 3 красных, 6 синих и 5 зеленых карандашей. Наугад вытаскиваются один из них. Найти вероятности событий того, что извлеченный карандаш красного цвета. |
| 2. | Бросаются два игральных кубика. Какова вероятность, что сумма выпавших очков равна 6. | Бросаются два игральных кубика. Какова вероятность, что сумма выпавших очков равна 8. |
| 3. | Слово ПЛОМБИР разрезается на буквы. Буквы перемешиваются и снова складываются слева направо. Найти вероятность того,что снова получится слово ПЛОМБИР. | Из буквы разрезной азбуки составлено слово ДОКУМЕНТ. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получится слово ДОКУМЕНТ |
| 4. | В пачке находятся одинаковые по размеру 10 тетрадей в линейку и 6 в клетку. Из пачки наугад берут 4 тетради. Какова вероятность того, что все 4 тетради окажутся в клетку? | На полке лежат 5 учебников и 6 художественных книг. С полки наугад снимают 3 книги. Какова вероятность того, что они окажутся учебниками? |
| 5. | На каждой из семи одинаковых карточек напечатана одна из букв: а, с, т, р, у, ж, л. Карточки тщательно перемешаны. Найти вероятность, что на четырех, вынутых по одной и расположенных «в одну линию» карточках можно будет прочесть слово «стул» | На каждой из семи одинаковых карточек напечатана одна из букв: д, а, т, о, с, ж, к. Карточки тщательно перемешаны. Найти вероятность, что на пяти, вынутых по одной и расположенных «в одну линию» карточках можно будет прочесть слово «доска» |
| 6. «5» | В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины. | В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников. |
| 7 «5» | В сборнике билетов по геометрии всего 25 билетов, в трех из них встречается вопрос о конусе. На экзамене школьник достается один случайно выбранный билет из этого сборника. Найти вероятность того, что в этом билете не будет вопроса о конусе. | В международных соревнованиях по фигурному катанию участвуют 25 спортсменок из разных стран, в том числе по три из США и России и по две из Японии и Швеции. Порядок выступления определяется жребием. Какова вероятность того, что спортсменка, выступающая первой, будет представлять какую-то другую из оставшихся стран? |
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Используя классическое определение вероятности, докажите свойства вероятности:-
Вероятность достоверного события равна 1. -
Вероятность невозможного события равна 0.
-
-
При каких условиях применима классическая формула определения вероятности? -
Какая сумма числа очков наиболее вероятна при бросании двух кубиков?
ЛИТЕРАТУРА
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007
Практическая работа № 3
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИЙ С ПОМОЩЬЮ ТЕОРЕМ УМНОЖЕНИЯ И СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
ЦЕЛЬ РАБОТЫ: научиться вычислять вероятности суммы совместных и несовместных событий, произведения независимых и зависимых событий.
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
-
Суммой A + B двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.-
Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий:
-
Р (А + В) = Р(А) + Р(В)
-
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В) = Р(А) + Р(В) – Р(АВ)
-
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий.-
Теорема произведения для независимых событий. Для независимых событий вероятность совместного появления событий равна произведению вероятностостей этих событий:
-
Р(АВ) = Р(А) Р(В).
-
Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(АВ) = Р(А) РА(В).
-
Вероятность появления хотя бы одного из независимых событий.
Если события А1, А2, А3,… Аn независимы в совокупности, причем Р(А1) = р1, Р(А2) = р2, Р(А3) = р3 и т.д.; q1, q2, q3, …, qn – вероятности противоположных событий.
Вероятность наступления события А, состоящего в наступлении хотя бы одного из событий А1, А2, А3,… Аn равна:
Р(А) = 1 – q1q2q3…qn.
-
Вероятность появления только одного из двух событий.
Р(А) = p1q2 + p2q1
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
| | I вариант | II вариант |
| 1. | Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий; английский и немецкий – 8%. Найти вероятность того, что случайно выбранный сотрудник фирмы знает хотя бы один язык. | Имеется 3 ящика, содержащих по 20 деталей. В первом ящике 12, во втором 5 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все детали окажутся стандартными. |
| 2. | Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,025; во второй – 0,03; в третий 0,019. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны. | В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: р, = 0,1; р, = 0,15; р, = 0,2. Найти вероятность того, что тока в цепи не будет (не работает хотя бы 1 элемент). |
| 3. | Имеется 3 ящика, содержащих по 15 деталей. В первом ящике 5, во втором 7 и в третьем 10 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все детали окажутся стандартными. | Среди студентов группы 15% имеют отличные оценки по математике, 34% – по истории. При этом 12% являются отличниками по обеим дисциплинам. Найти вероятность того, что случайно выбранный студент учится на «отлично» хотя бы по одной дисциплине. |
| 4. | Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. | В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена. Решить задачу двумя способами. |
| 5. | На полке стоят 6 учебников по математике и 3 по информатике. С полки наудачу берется сначала один учебник. Потом второй. Найти вероятность, что первая взятая книга будет учебником по информатике, а вторая учебником по математике. | В ящике находится 8 стандартных и 6 нестандартных детали. Наудачу вынимается сначала одна деталь, а потом вторая. Найти вероятность, что первая взятая деталь стандартная, а вторая нестандартная. |
| 6. | Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент. | Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из двух проверенных изделий только одно высшего сорта. |
| 7. | На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие А). Решить задачу двумя способами. | Мастер обслуживают 5 станков. 20% рабочего времени он проводит у первого станка, 10% - у второго, 15% - у третьего, 25% - у четвертого, 30% - у пятого станка. Найти вероятность того, что в наудачу выбранный момент времени мастер находится у 1, или 2, или 3 станка. |
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Чем отличается операция сложения вероятностей от произведения? -
Запишите способы, которыми можно рассчитать вероятность появления хотя бы одного события?
ЛИТЕРАТУРА
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007.
Практическая работа № 4
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИЙ С ПОМОЩЬЮ ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И ФОРМУЛЫ БАЙЕСА
ЦЕЛЬ РАБОТЫ: научиться вычислять вероятности сложных событий с помощью формулы полной вероятности и формулы Байеса.
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Формула полной верятности позволяет определить вероятность события А, которое может наступить при условии появления одного из несовместных событий В1, В2, … Вn, образующих полную группу.
Р(А) = Р(В1)·РВ1(А) + Р(В2)·РВ2(А) + … + Р(Вn)·РВn(А)
Чтобы оценить вероятности гипотез В1, В2, … Вn, после того как стал известен результат испытания, используется формула Байеса.
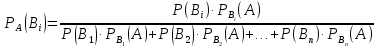
Пример 1. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором 30 деталей, из них 24 стандартных; в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – стандартная.
Решение
-
Обозначим через А – событие«взятая наудачу деталь стандартна»
Событие В1 – деталь извлечена из первого ящика;
Событие В2 – деталь извлечена из второго ящика
Событие В3 – деталь извлечена из третьего ящика
-
Определим вероятности событий В1, В2 и В3.
Вероятность того, что деталь взята из первого ящика Р(В1) = 1/3
Вероятность того, что деталь взята из первого ящика Р(В2) = 1/3
Вероятность того, что деталь взята из первого ящика Р(В3) = 1/3
-
Определим условные вероятности.
Условная вероятность того, что из 1 ящика была извлечена стандартная деталь: РВ1(А) =
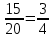
Условная вероятность того, что из 2 ящика была извлечена стандартная деталь: РВ2(А) =
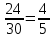
Условная вероятность того, что из 3 ящика была извлечена стандартная деталь: РВ3(А) =
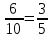
-
По формуле полной вероятности определим вероятность события А:
Р(А) =
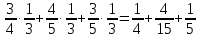 =
= 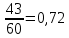 . Ответ: Р(А) = 0,72
. Ответ: Р(А) = 0,72Пример 2. На заводе, изготовляющем болты, первая машина производит 25%, вторая - 35%, третья - 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%.Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой машиной?
Решение
-
Обозначим через А – событие «выбран болт с дефектом»
В1 – болт произведен 1 машиной; В2 – болт произведен 2 машиной; В3 – болт произведен 3 машиной
-
По условию задачи имеем:
Р(В1) = 0,25
Р(В2) = 0,35
Р(В3) = 0,4
РВ1(А) = 0,05
РВ2(А) = 0,04
РВ3(А) = 0,02
-
По формуле Байеса определим вероятность гипотезы В, при условии что выбран болт с дефектом:
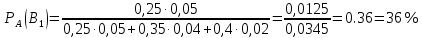
Ответ:
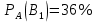
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
I вариант
-
В ящике содержится 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей – на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0,9; для деталей, изготовленных на заводах №2 и №3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества. -
Два оператора набили по одинаковому комплекту перфокарт. Вероятность того, что первый оператор допустит ошибку, равна 0,1; для второго оператора эта вероятность равна 0,2. При сверке перфокарт была обнаружена ошибка. Какова вероятность того, что ошибся первый оператор? -
Два оператора набили по одинаковому комплекту перфокарт. Вероятность того, что первый оператор допустил ошибку, равна 0,15, второй - 0,1. Какова вероятность, что при проверке наудачу взятая перфокарта оказалась с ошибкой? -
В магазин поступили телевизоры от 3 фирм. На долю 1 фирмы приходится 50% от общего числа поставок, на долю 2 фирмы – 20%, а на долю 3 фирмы – 30%. Из практики известно, что бракованными оказываются 4% поставляемых 1 фирмой, 3% поставляемых 2 фирмой и 5% поставляемых 3 фирмой. Найти вероятность того, что купленный в магазине и оказавшийся бракованным телевизор, был произведён первой фирмой.
II вариант
-
В магазин поступили телевизоры от 3 фирм. На долю 1 фирмы приходится 50% от общего числа поставок, на долю 2 фирмы – 20%, а на долю 3 фирмы – 30%. Из практики известно, что бракованными оказываются 4% поставляемых 1 фирмой, 3% поставляемых 2 фирмой и 5% поставляемых 3 фирмой. Найти вероятность того, что купленный в данном магазине телевизор окажется бракованным. -
В больницу поступает в среднем 50% больных с заболеванием А, 30% с заболеванием В, 20% с заболеванием С. Вероятность полного выздоровления для каждого заболевания соответственно равна 0,7; 0,8; 0,9. Больной был выписан из больницы здоровым. Найти вероятность того, что он страдал заболеванием А. -
На сборку механизма поступают детали с двух автоматов. Первый автомат в среднем дает 1,5% брака, второй – 1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго – 1500. -
Завод выпускает 3 типа предохранителей для магнитофона. Доля каждого из них в общем объеме составляет 30, 50 и 20%. При перегрузке сети предохранитель 1 типа срабатывает с вероятностью 0,8%, 2 типа 0,9 и 3 типа 0,85%. Выбранный наугад предохранитель сработал при перегрузке сети. Какова вероятность того, что он принадлежал к 1 типу?
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Для чего используется формула Байеса?
Литература
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.
Практическая работа № 5
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТИ ПОЯВЛЕНИЯ СОБЫТИЯ
ПРИ ПОВТОРЕНИИ ИСПЫТАНИЙ
ЦЕЛЬ РАБОТЫ: научиться вычислять вероятности событий с помощью формул Бернулли, Пуассона и Муавра-Лапласа.
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами
смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Формула Бернулли позволяет рассчитать вероятность того, что при n испытаниях событие А осуществится ровно k раз. Формулой Бернулли удобно пользоваться, когда n и k<10.
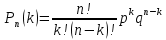
Если n и k велики, то для нахождения вероятности появления события k раз в n испытаниях используется локальная теорема Муавра-Лапласа или асимптотическая формула Лапласа.
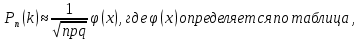
Если n велико, k мало и p<0,1, то для нахождения вероятности появления события k раз в n испытаниях удобно пользоваться формулой Пуассона.
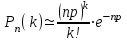
Пример 3. В классе 10 компьютеров. Для каждого компьютера вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность, что в данный момент: а) включено 4 компьютера; б) включены все компьютеры; в) включено менее 3 компьютеров; г) включено не менее 3 компьютеров.
Решение
а) n = 10; k = 4; p = 0,8; q = 0,2
По формуле Бернулли: Р10(4) =
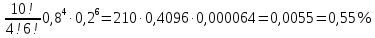
б) n = 10; k = 10; p = 0,8; q = 0,2
По формуле Бернулли: Р10(10) =
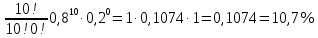
в) Р10(k<3) = Р10(0) + Р10(1) + Р10(2)
Р10(0)=
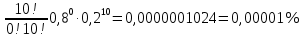
Р10(1)=
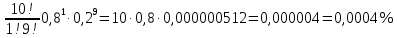
Р10(2)=
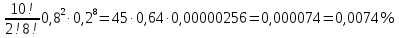
Р10(<3) =
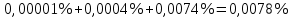
г) Т.к. события «включено менее 3 компьютеров» и «включено не менее трех компьютеров» являются противоположными, то
Р10(k≥3) = 1 - Р10(<3) = 1 – 0,000078 = 0,9999 = 99, 99%
Ответ: Р10(4) = 0,55%; Р