Файл: Методические указания для студентов по практическим занятиям по учебной дисциплине.doc

Вставьте оценки по своему желанию.

Проходной балл — среднее значение всех оценок.

Итог относительно проходного балла: если средний балл меньше проходного — «Надо работать», иначе — «Победитель».

Условия зачисления: если количество «2» = 0 и средний балл больше или равен проходному — «зачислен», иначе — «не зачислен».

2. 
   Создайте форму для ввода данных.
   
3. 
   Запишите все функции и формулы, которые использовались во время работы.
   
4. 
   Сохраните под своим именем и номером группы.
   
5. 
   Составьте отчет. Закончите работу.
   

Задание №4. Сделать вывод о проделанном практическом занятии:



Содержание отчета:
Отчет должен содержать:

1. 
   Название работы.
   
2. 
   Цель работы.
   
3. 
   Задание и его решение.
   
4. 
   Вывод по работе.
   

Вопросы для закрепления теоретического материала к практическому занятию:

1. 
   Что представляет собой электронная таблица?
   
2. 
   Как формируется адрес ячейки?
   
3. 
   Что такое диапазон ячеек и как он задается?
   
4. 
   Чем различаются абсолютная и относительная ссылка?
   
5. 
   Как связываются листы одной книги?
   

Практическое занятие №18.

Тема: Решение систем уравнений.

Цель: Научиться решать системы линейных уравнений с помощью MS Excel.

Оборудование и раздаточный материал: персональный компьютер, стандартный пакет MS Word

Краткие теоретические сведения и учебно-методические материалы по теме практического занятия:
А.Решим систему 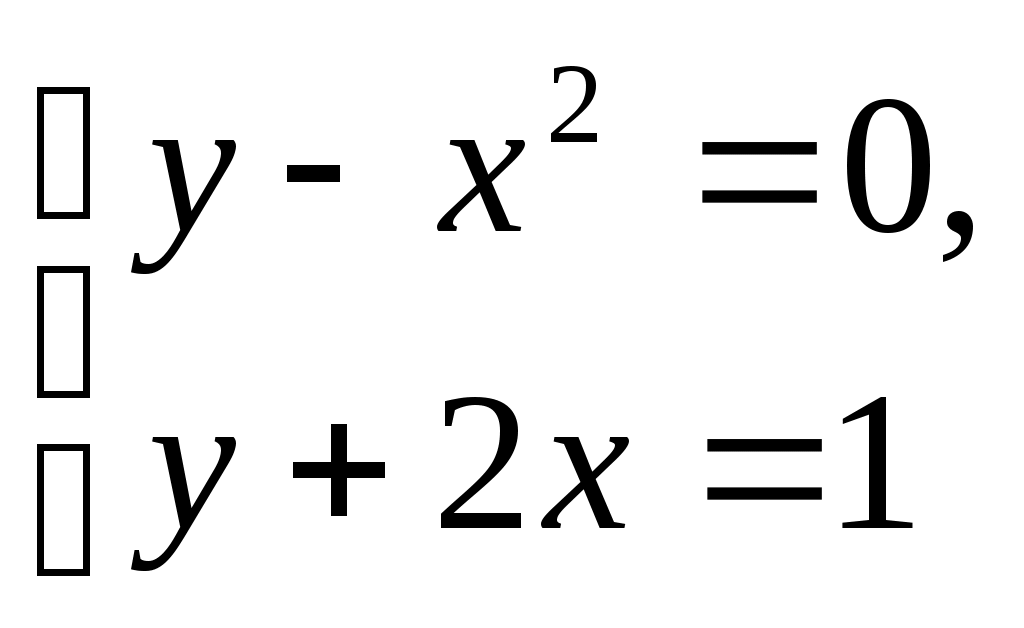графическим способом. П 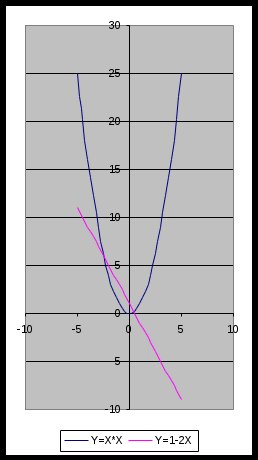реобразуем данную систему 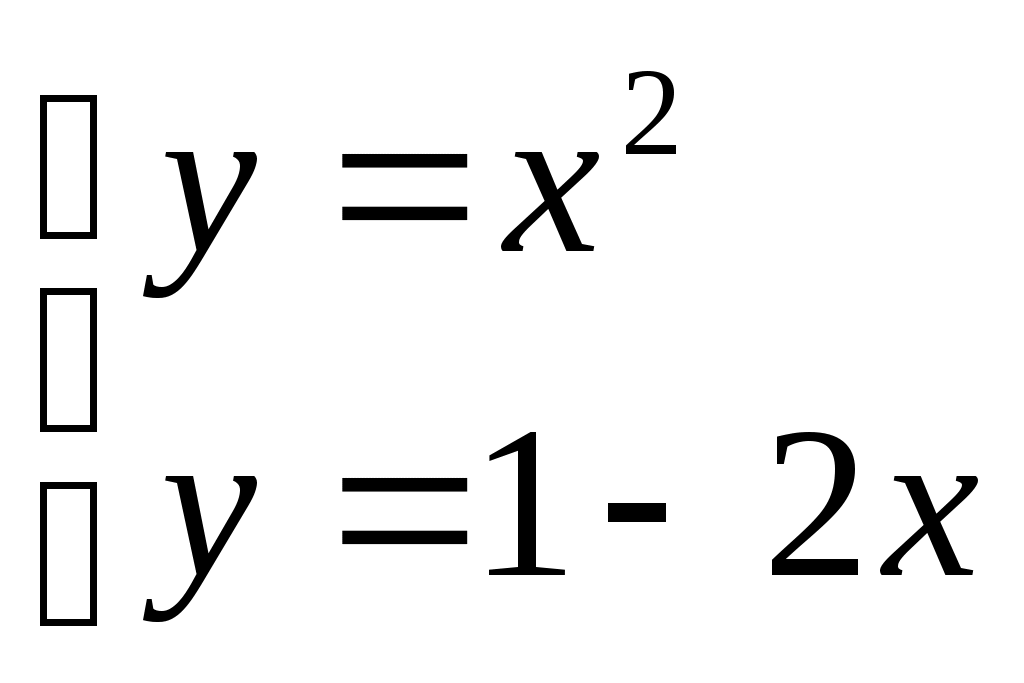. Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз

---

, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу =1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы. {(-2,5; 6); (0,5; 0)}

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.

Запишем алгоритм решения систем уравнений графическим способом:

1. Преобразовать систему уравнений, если это необходимо.

2. Задать начальные значения для Х

3. Найти значение первой функции при заданных Х

4. Найти значение второй функции при тех же Х

5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы

6. Решение системы - точка пересечения графиков функций.

7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

Б. Решить систему уравнений 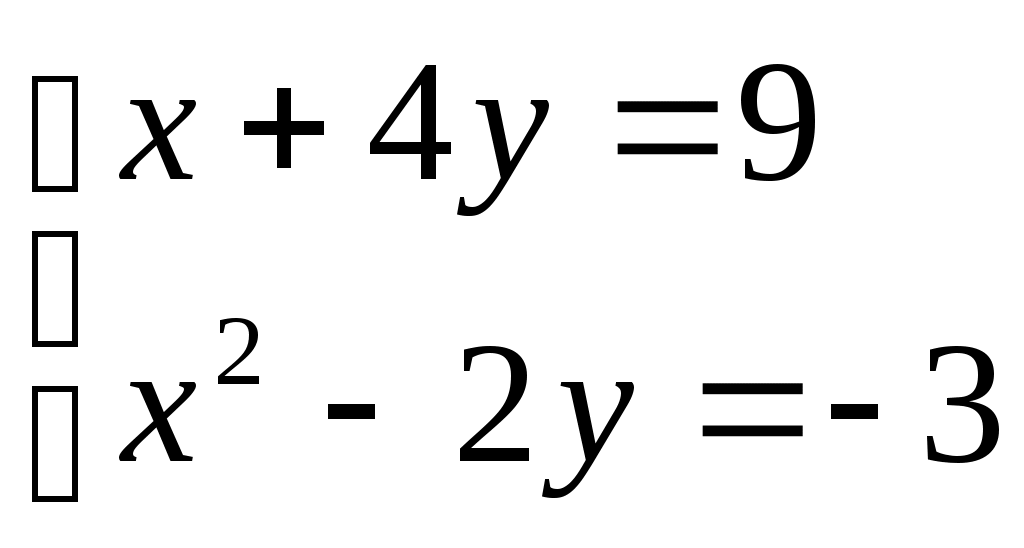. Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:. Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения

1. Преобразовать систему уравнений, если это необходимо

2 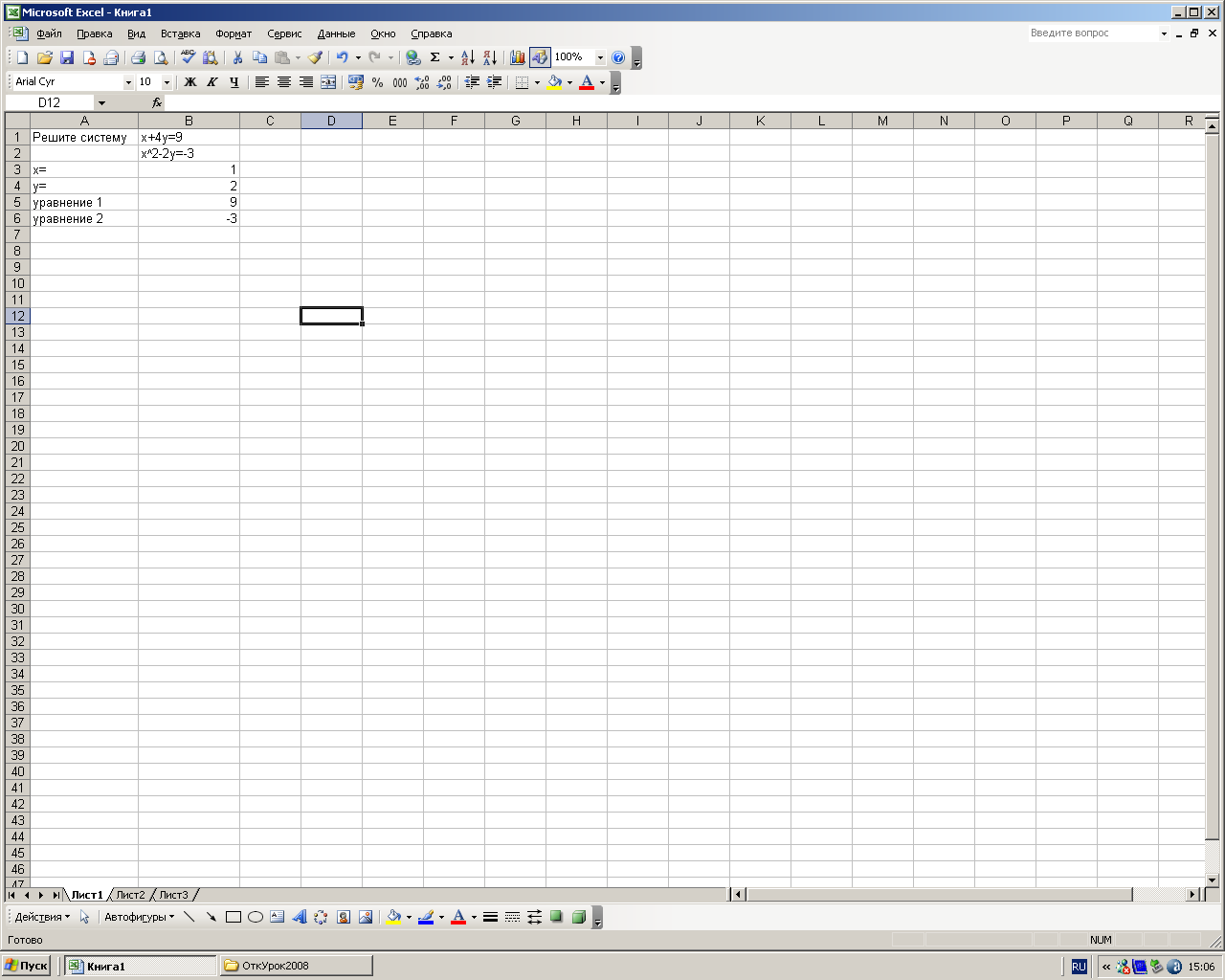. Записать исходные данные (в ячейку А1 ввести текст «Решите уравнение», в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст «Х=», в ячейку А4 «Y=», в ячейку А5 «уравнение 1», в ячейку А6 «уравнение 2». В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.

3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.

---

4. Выбрать команду Сервис – Поиск решения.

5. Установить целевую ячейку - ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения

6. В поле «изменяя ячейки» указать ячейки, в которых хотим увидеть ответ (В3 и В4)

7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак «=», в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК

8. Решить систему уравнений, щелкнув кнопкой Выполнить
Ход работы:
Решим систему уравнений

5х₁ + 4х₂ + 5х₃ = 2400

4х₁ + 3х₂ + х₃ = 1450

5х₁ + 2х₂ + 3х₃ = 1550.

Количество переменных в системе уравнений должно быть равно количеству уравнений.Уравнения должны быть записаны в стандартной форме. Если это необходимо, используйте основы алгебры и перепишите уравнение так, чтобы все переменные отображались по левую сторону от знака равенства.  В нашем примере уравнения приведены в стандартном виде.

Запишем систему уравнений в матричном виде: АХ = В, где

	5 4 5		х1		2400
А =	4 3 1 ;	Х =	х2 ;	В =	1450 .
	5 2 3		х3		1550

Если определитель системы отличен от нуля, т.е. |А|≠0, то решение системы можно найти по формуле:

X = А^-1В,

где А^-1 – обратная матрица.

Таким образом, для нахождения корней системы уравнений необходимо:

- вычислить определитель матрицы А (функция МОПРЕД);

- найти обратную матрицу А^-1 (функция МОБР);

- найти произведение матриц А^-1В (функция МУМНОЖ).

Примечание. Систему уравнений можно решить по формуле Крамера:

---

где D – определитель системы;

D_i – определитель матрицы А_i, получаемой из матрицы А заменой i-го столбца (т.е. столбца коэффициентов при неизвестном х_i) вектором свободных членов.

Решение системы линейных уравнений в Excel

Распределим ячейки рабочего листа (рис. 2).

1. В указанные ниже ячейки введем значения элементов матриц А и В:

a) в диапазон ячеек D4: F6 введем значения элементов матрицы А;

b) в диапазон ячеек I4:I6 введем значения элементов столбца В.

2. Для размещения элементов обратной матрицы А^-1 отведем блок ячеек D8: F10.

3. Для размещения результата (для переменных х_i, i = 1, 2, 3) отведем диапазон ячеек I8:I10.



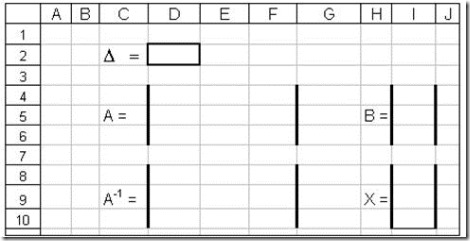
Рис. 2

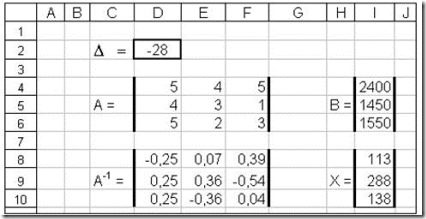
Убедимся, что определитель матрицы А отличен от нуля. Для этого в ячейку D2 введем формулу =МОПРЕД(D4:F6). В ячейке D2 получили результат –28. Следовательно, матрица А имеет обратную.

Вычислим обратную матрицу А^-1. Для этого выполним следующие действия.

1. Выделим для результата блок ячеек D8:F10, начиная с ячейки D8;

2. Выполним командуВставка –> Функция –> МОБР –> ОК.

3. В поле Массив введем адреса ячеек, где размещены элементы матрицы А, т.е. D4:F6.

4. Нажмем клавиши Shift + Ctrl + Enter.

Результат вычисления отобразится в ячейках D8:F10 (рис. 3).

Чтобы найти элементы столбца Х, умножим обратную матрицу А^-1на столбец В. Для этого выполним следующие действия:

1. Выделим диапазон ячеек I8:I10;

2. Выполним командуВставка –> Функция –> МУМНОЖ –> ОК.

3. В поле Массив1 введем адреса ячеек, где размещены элементы матрицы А^-1, т.е. D8:F10, а в полеМассив2 – адреса ячеек, где размещен столбец В, т.е. I4:I6;

4. Нажмем клавиши Shift + Ctrl + Enter.

Результат вычисления появится в ячейках I8:I10 (рис. 3).Получили решение системы уравнений х₁ = 113; х₂ = 288; х₃ = 138.



Задание №3. Сделать вывод о проделанном практическом занятии:


Содержание отчета:

---

Отчет должен содержать:

1. 
   Название работы.
   
2. 
   Цель работы.
   
3. 
   Задание и его решение.
   
4. 
   Вывод по работе.
   

Вопросы для закрепления теоретического материала к практическому занятию:

1. 
   Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel.
   
2. 
   Порядок действий для решения системы уравнений матричным методом в MS Excel.
   
3. 
   Методика работы с надстройкой «Подбор параметра» для нахождения корней уравнений.
   
4. 
   Методика работы с надстройкой «Поиск решения» для нахождения корней нелинейных уравнений и решения системы линейных алгебраических уравнений.
   

.

---