Выпускник получит возможность научиться:

• 
  Выводить уравнение сферы в заданной прямоугольной системе координат
  
• 
  Доказывать теоремы о касательной плоскости к сфере.
  

---

Объемы тел

Понятие объема и его свойства. Объем цилиндра, прямоугольного параллелепипеда и призмы. Принцип Кавальери. Объем пирамиды. Объем конуса и усеченного конуса. Объем шара и его частей. Площадь поверхности многогранника, цилиндра, конуса, усеченного конуса. Площадь поверхности шара и его частей.

Выпускник научится:

• 
  Вводить понятие объема тела;
  
• 
  Применять свойства объемов, теорему об объеме прямоугольного параллелепипеда при решении задач;
  
• 
  Применять следствие об объеме прямой призмы, основанием которой является прямоугольный треугольник при решении задач;
  
• 
  Применять теоремы об объемах прямой призмы и цилиндра при решении задач;
  
• 
  Понимать возможность и целесообразность применения определенного интеграла для вычисления объемов тел;
  
• 
  Применять формулу объема наклонной призмы с помощью интеграла при решении задач;
  
• 
  Применять теорему об объеме пирамиды и, как следствие, формулу объема усеченной пирамиды при решении типовых задач;
  
• 
  Решать типовые задачи на применение формул объемов конуса и усеченного конуса;
  
• 
  Применять формулы объема шара и площади сферы при решении задач.
  

Выпускник получит возможность научиться:

• 
  Доказывать теоремы об объемах прямой призмы и цилиндра;
  
• 
  Выводить формулу объема наклонной призмы с помощью интеграла;
  
• 
  Выводить формулу объема усеченной пирамиды;
  
• 
  Доказывать теорему об объеме конуса и ее следствие, в котором выводится формула объема усеченного конуса;
  
• 
  Вывести формулы объема шара и площади сферы при решении задач;
  
• 
  Использовать формулы для вычисления объемов частей шара – шарового сегмента, шарового слоя и шарового сектора.
  

Предметные результаты освоения учебного предмета «Математика», отражающие НРЭО:

– формирование представлений о математике, её роли в жизни и профессиональной деятельности человека, необходимость применения математических знаний для решения современных практических задач человечества, своей страны и родного края, в том числе с учетом рынке труда Челябинской области;

– овладение основными навыками получения, применения, интерпретации и презентации информации математического содержания, использования математических знаний в повседневной жизни и изучения других предметов, формирование представлений о реальном секторе экономики и рынке труда Челябинской области;

---

– формирование представлений об особенностях деятельности людей, ведущей к развитию промышленности родного края, освоение системы математических знаний для последующего изучения дисциплин необходимых для получения инженерных и технических специальностей в учреждениях системы среднего и высшего профессионального образования и для самообразования.
Содержание тем учебного курса.
Алгебра и начала математического анализа 10 класс
Повторение курса Алгебры 7 – 9 классы

Решение уравнений. Решение систем. Решение неравенств. Метод интервалов для решения неравенств. Функции, их свойства и графики.

Числовые функции

Определение функции, способы ее задания, свойства функций. Обратная функция.

Тригонометрические функции

Числовая окружность. Длина дуги единичной окружности. Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Формулы приведения. Функция у=sin x, ее свойства и график. Функция у=cos x, ее свойства и график. Периодичность функций у = sin х, у= соs х. Построение графика функций y=mf(x) и y=f(kx) по известному графику функции y=f(x). Функции у=tg х к у = ctg х, их свойства и графики.

Тригонометрические уравнения

Первые представления о решении тригонометрических урав-нений. Арккосинус. Решение уравнения cos t= a. Арксинус. Решение уравнения sin t= а. Арктангенс и арккотангенс. Решение уравнений tg х = a, ctg x = a.

Простейшие тригонометрические уравнения. Два метода решения тригонометрических уравнений: введение новой переменной и разложение на множители. Однородные тригонометрические уравнения.

---

Преобразование тригонометрических выражений

Синус и косинус суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.

Производная

Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.

Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии.

Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.

Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Дифференцирование функции у = f(kx+ т).

Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции у = f(x).

Применение производной для исследования функций на монотонность и экстремумы. Построение графиков функций. Применение производной для отыскания наибольших и наименьших значений величин.

Обобщающее повторение (11ч)
Алгебра и начала математического анализа 11 класс



Повторение курса Алгебры и начала математического анализа 10 класс

Степени и корни. Степенные функции

Понятие корня n-й степени из действительного числа. Функции 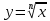, их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики.

Показательная и логарифмическая функции

Показательная функция, ее свойства и график. Показательные уравнения. Показательные неравенства.

Понятие логарифма. Функция у = log_ax, ее свойства и график. Свойства логарифмов. Логарифмические уравнения. Логарифмические неравенства. Переход к новому основанию логарифма. Дифференцирование показательной н логарифмической функций.

---

Первообразная и интеграл

Первообразная. Правила отыскания первообразных. Таблица основных неопределенных интегралов.

Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла. Формула Ньютона — Лейбни­ца. Вычисление площадей плоских фигур с помощью определен­ного интеграла.

Элементы математической статистики, комбинаторики и тео­рии вероятностей

Статистическая обработка данных. Простейшие вероятностные задачи. Сочетания и размещения. Формула бинома Ньютона. Случайные события и их вероятности.

Уравнения и неравенства. Системы уравнений и неравенств

Равносильность уравнений. Общие методы решения уравнений: замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x), разложение на множители, введение новой переменной, функционально-графический метод.

Решение неравенств с одной переменной. Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства с модулями.

Системы уравнений. Уравнения и неравенства с параметрами.

Обобщающее повторение
Геометрия 10 класс



1. Введение.

Предмет стереометрии. Аксиомы стереометрии. Некоторые следствия из аксиом.

Основная цель – познакомить учащихся с содержанием курса стереометрии,с основнымипонятиями и аксиомами, принятыми в данном курсе, вывести первые следствия из аксиом, дать представление о геометрических телах и их поверхностях, об изображении пространственных фигур на чертеже, о прикладном значении геометрии.

Изучение стереометрии должно базироваться на сочетании наглядности и логической строгости. Опора на наглядность – непременное условие успешного усвоения материала, и в связи с этим нужно уделить большое внимание правильному изображению на чертеже пространственных фигур. Однако наглядность должна быть пронизана строгой логикой. В отличие от курса планиметрии в курсе стереометрии уже с самого начала формулируются аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве, и далее изучение свойств взаимного расположения прямых и плоскостей проходит на основе этих аксиом. Тем самым задается высокий уровень строгости в логических рассуждениях, который должен выдерживаться на протяжении всего курса.

---

Смотрите также файлы

• Английский, как глобальный язык общения.docx

• Ортопедическое лечение при повышенной стираемости зубов..docx

• 1. Близорукость Фокусировка зрения на мониторе компьютера, который находится на определенном расстоянии от человека вследствие чего возникает застой сетчаткиотслоение сетчатки пропадает фокусировка зрения.doc

• Психология Задание 5.docx

• Контрольная работа по дисциплине Культурология По теме Языческая культура восточных славян.docx