Файл: 1. введение в линейное программирование.doc

1.ВВЕДЕНИЕ В ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

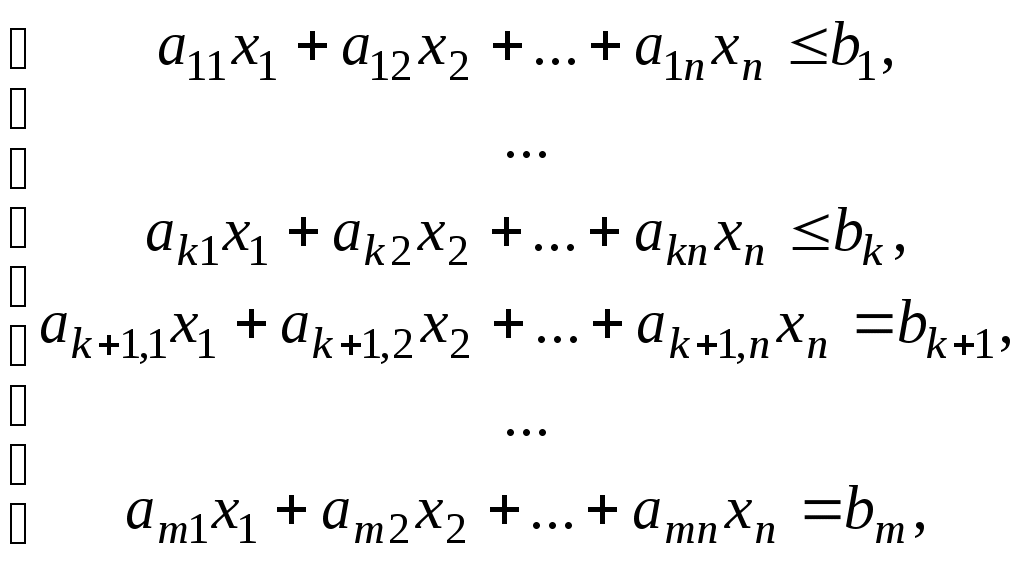
Линейное программирование (ЛП) – это метод оптимизации моделей, в которых целевые функции и ограничения строго линейны.ЛП успешно применяется в военной области, индустрии, сельском хозяйстве, транспортной отрасли, экономике, системе здравоохранения и даже в социальных науках. Задача, в которой требуется найти экстремум функции при ограничениях:называется задачей линейного программирования.Задача в краткой записи имеет вид

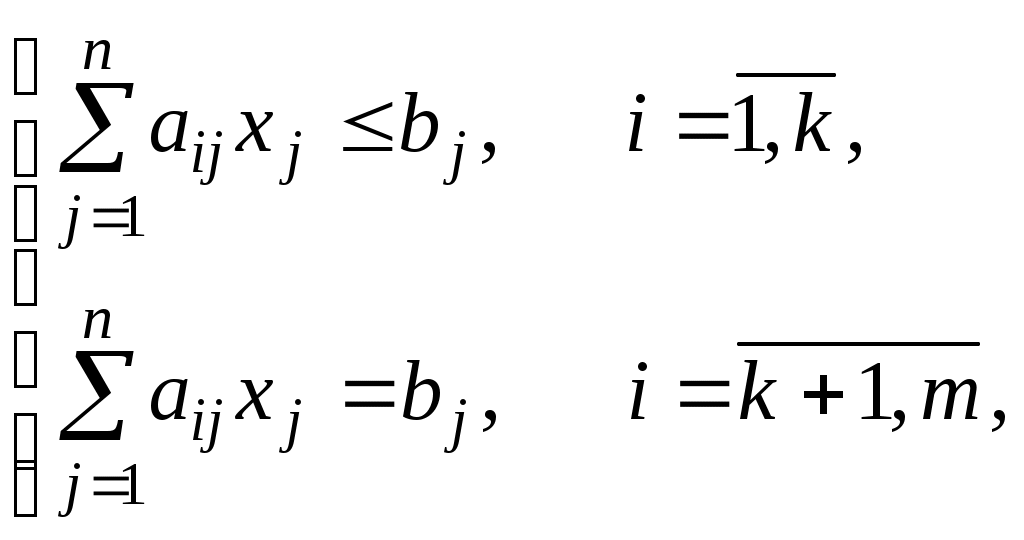
1.1.Модели линейного программирования с двумя
переменными

Пример 2.1. Компания Mikks производит краску для внутренних и наружных работ из сырья двух типов С1 и С2. Следующая таблица представляет основные данные для задачи.

	Расход сырья (в тоннах) на тонну краски		Максимально возможный ежедневный расход сырья
	Для наружных работ	Для внутренних работ
Сырье С1	6	4	24
Сырье С2	1	2	6
Доход (в тыс. долл.) на тонну краски	5	4

Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более, чем на 1 т аналогичный показатель производства краски для внешних работ. Компания хочет определить

---

оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.Задача (модель) линейного программирования (ЗЛП), как и любая задача исследования операций, включает три основных элемента.

1. 
   Переменные, которые следует определить.
   
2. 
   Целевая функция, подлежащая оптимизации.
   
3. 
   Ограничения, которым должны удовлетворять переменные.
   

Определение переменных – первый шаг в создании модели. В нашем примере необходимо определить ежедневные объемы производства краски для внутренних и наружных работ. Обозначим эти объемы как переменные модели: ежедневный объем производства краски для наружных работ; ежедневный объем производства краски для внутренних работ.Используя эти переменные, далее строим целевую функцию. Логично предположить, что целевая функция, как суммарный ежедневный доход, должна возрастать при увеличении ежедневных объемов производства красок. Обозначим эту функцию через z (она измеряется в тысячах долларов) и положим, что .В соответствии с целями компании получаем задачу:Максимизировать , или Итак, остался не определенным последний элемент модели  условия (ограничения), которые должны учитывать ограниченные возможности ежедневного потребления сырья и ограниченность спроса на готовую продукцию. 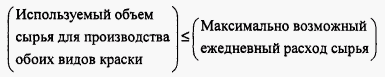Другими словами, ограничения на сырье можно записать следующим образом.Из таблицы с данными имеем следующее.Используемый объем сырья (т)Используемый объем сырья (т)Поскольку ежедневный расход сырья С1 и С2 ограничен соответственно 24 и 6 тоннами, получаем следующие ограничения.

---

(сырье С1)

(сырье С2)

Существует еще два ограничения по спросу на готовую продукцию:

1. 
   максимальный ежедневный объем производства краски для внутренних работ не должен превышать 2 т, т.е.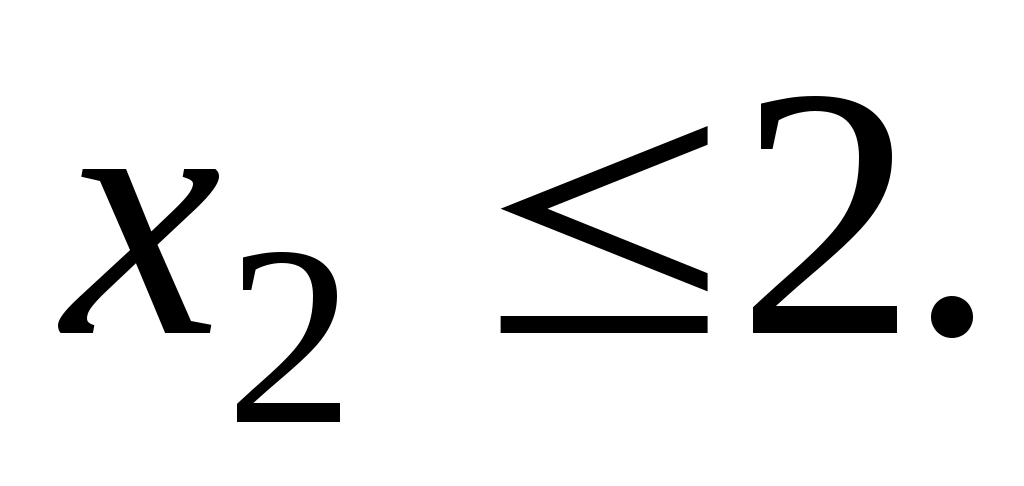
   
2. 
   ежедневный объем производства краски для внутренних работ не должен превышать ежедневный объем производства краски для наружных работ более чем на одну тонну (разность между ежедневными объемами производства красок для внутренних и наружных работ не должна превышать одной тонны), т.е.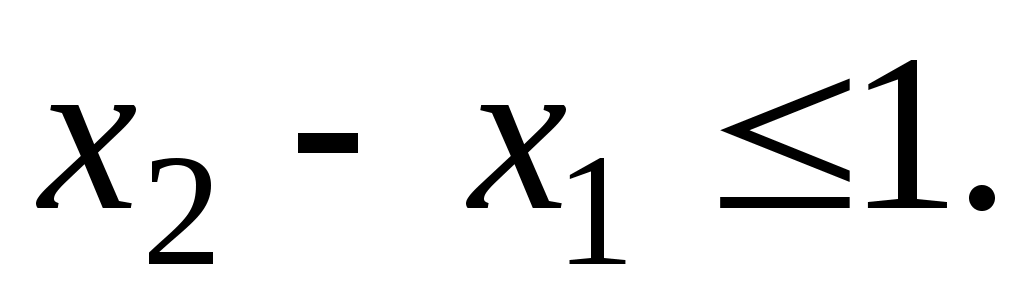
   

Еще одно неявное ограничение состоит в том, что переменные и должны быть неотрицательными. Таким образом, к сформулированным выше ограничениям необходимо добавить условие неотрицательности переменных: , . Окончательно задача будет записана следующим образом:Максимизировать (или )при выполнении следующих ограничений: , .Любое решение, удовлетворяющее ограничениям модели, является допустимым. Например, решение и будет допустимым, так как не

---

нарушает ни одного ограничения, включая условие неотрицательности. Чтобы удостовериться в этом, подставьте значения и в левые части неравенств системы ограничений и убедитесь, что ни одно неравенство не нарушается. Значение целевой функции при этом решении будет равно (тысяч долларов).

Итак, задача сформулирована.

Теперь встает вопрос о нахождении оптимального допустимого решения, доставляющего максимум целевой функции. После некоторых раздумий приходим к выводу, что задача имеет много (фактически, бесконечно много) допустимых решений. По этой причине невозможна подстановка значений переменных для поиска оптимума, т.е. нельзя применить простой перебор всех допустимых решений. Следовательно, необходима эффективная процедура отбора допустимых решений для поиска оптимального.

---

1.2.Графическое решение ЗЛП

Графический способ решения задачи ЛП состоит из двух этапов.

1. 
   Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.
   
2. 
   Нахождение оптимального решения среди всех точек пространства допустимых решений.
   

1.2.1.Нахождение максимума целевой функции

Используем модель, построенную для компании Mikks, чтобы показать два этапа графического решения ЗЛП.Этап 1.Построение пространства допустимых решений.Сначала проведем оси: на горизонтальной будут указываться значения переменной , а на вертикальной  (рис. 2.1). Далее рассмотрим условие неотрицательности переменных: , . 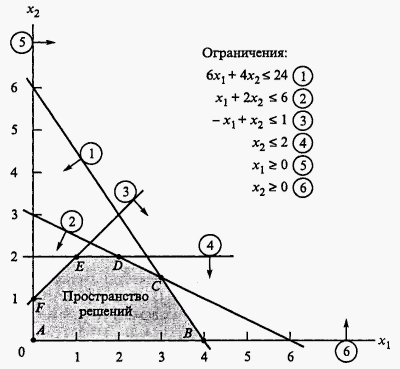Эти два ограничения показывают, что пространство допустимых решений будет лежать в первом квадранте.Рис. 2.1. Пространство допустимых решений моделиЧтобы учесть оставшиеся ограничения, проще всего заменить неравенства на равенства, в результате чего получим уравнения прямых, а затем на плоскости провести эти прямые. Например, неравенство заменяется уравнением прямой . Эта прямая обозначена на рис. 2.1 как линия (1).Этап 2. Нахождение оптимального решения.Точки пространства допустимых решений, показанного на рис. 2.1, удовлетворяют одновременно всем ограничениям. Это пространство ограничено отрезками прямых, которые соединяются в угловых точках А, В, С, D, Е и F. Любая точка, расположенная внутри или на границе области, ограниченной ломаной ABCDEF, является допустимым решением, т.е. удовлетворяет всем ограничениям. Поскольку пространство допустимых

---