Добавлен: 11.01.2024
Просмотров: 119
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
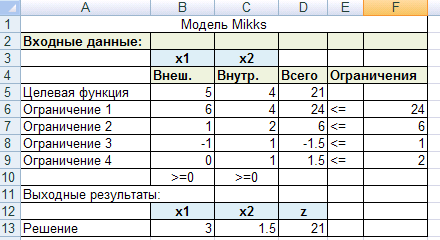
В этом окне надо ввести адрес ячейки, в которой вычисляется значение целевой функции, указать, надо ли минимизировать или максимизировать целевую функцию, и ввести адреса ячеек, содержащих значение переменных. В нашей модели:
-
в поле ввода УСТАНОВИТЬ ЦЕЛЕВУЮ ЯЧЕЙКУ вводится D5; -
устанавливается переключатель РАВНОЙ МАКСИМАЛЬНОМУ ЗНАЧЕНИЮ; -
в поле ввода ИЗМЕНЯЯ ЯЧЕЙКИ вводится $B$13:$C$13.
Эта информация указывает средству ПОИСК РЕШЕНИЯ, что переменные находятся в ячейках В13 и С13, и надо найти максимум целевой функции, значение которой вычисляется в ячейке D5.
Далее надо задать ограничения модели, щелкнув на кнопке ДОБАВИТЬ в диалоговом окне ПОИСК РЕШЕНИЯ. Открывшееся диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ предоставляет средства для ввода всех частей ограничений (левой части, знака неравенства и значения правой части). Используя это окно, вводим ограничения модели в таком виде: $D$6:$D$9<=$F$6:$F$9 (напомним, что в ячейках F6:F9 записаны значения правых частей ограничений).
Теперь осталось ввести ограничения неотрицательности для переменных. С помощью диалогового окна ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ вводим $B$13:$C$13>=0.
Когда ПОИСК РЕШЕНИЯ найдет решение этой задачи, оптимальное значение целевой функции появится в ячейке D5, а значения переменных
Теперь все готово для решения нашей задачи, достаточно щелкнуть на кнопке ВЫПОЛНИТЬ в диалоговом окне ПОИСК РЕШЕНИЯ, для чего надо открыть диалоговое окно ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ, щелкнув на кнопке ПАРАМЕТРЫ.
Самое важное – установить опцию ЛИНЕЙНАЯ МОДЕЛЬ. В этом же окне можно указать, что все переменные должны быть неотрицательными (опция Неотрицательные значения).
Результат работы:
1.4.Двойственная задача и ее решение
Каждой задаче линейного программирования можно определённым образом поставить в соответствие некоторую другую задачу линейного программирования, называемую сопряжённой или двойственной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции при ограничениях "с недостатком".
Две следующие задачи называются симметричными взаимно двойственными задачами линейного программирования:
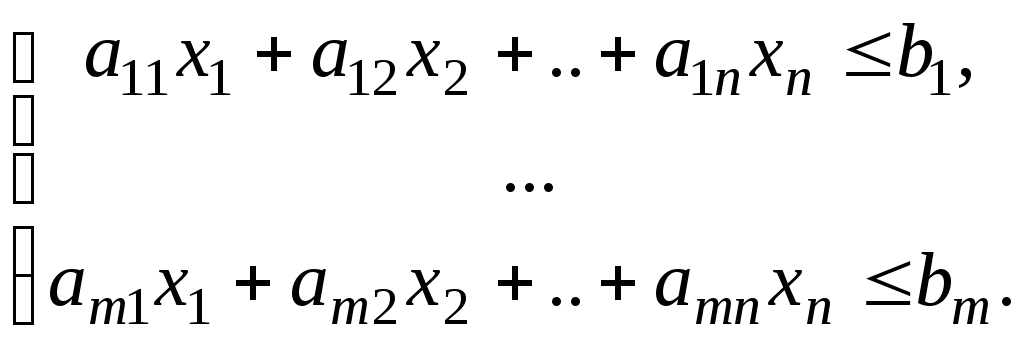 | 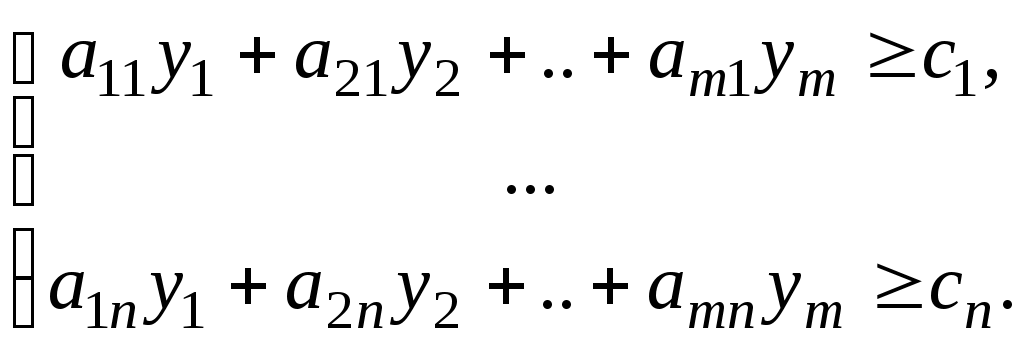 |
Обе двойственные задачи линейного программирования обладают следующими свойствами:
-
в одной задаче ищут максимум целевой функции, в другой минимум; -
обе задачи являются стандартными задачами линейного программирования, причем в задаче о максимуме все неравенства вида "≤", а в задаче о минимуме вида "≥" ; -
матрица системы ограничений одной задачи является транспонированной к матрице системы ограничений другой; -
коэффициенты при переменных целевой функции одной задачи являются свободными членами ограничений другой; -
число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче; -
условия неотрицательности имеются в обеих задачах.
Свойствами двойственных задач следует руководствоваться при их составлении.
1.5.Целочисленное программирование
Значительная часть задач по смыслу может иметь решения только в целых числах; например, число турбин, судов, животных может быть только целым числом. Такие задачи решаются методами целочисленного программирования. Общая постановка задачи линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.
Задачи целочисленного программирования решаются в Excel теми же средствами, что и общие задачи линейного программирования. В отличие от задач линейного программирования, при решении задач целочисленного программирования необходимо добавить указание на то, что разыскиваемые оптимальные значения переменных могут принимать только целые значения. Для этого в окне "Добавление ограничения" нужно выбрать в списке, расположенном посередине, значение "цел", как показано в следующем примере.
Пример 2.3. На мебельной фабрике изготавливают столы, стулья и табуреты. На производство одного изделия требуется 1,5, 1 и 0,62 м3 древесины. При этом затраты рабочего времени при изготовлении стола составляют 5 машино-часов, стула − 1,5 машино-часа и табурета − 0,7 машино-часа. Всего для производства мебели фабрика может ежедневно использовать 12 м3 древесины. Оборудование может быть занято в течение 26 машино-часов. Прибыль от реализации стола, стула и табуретки равна 200, 30 и 15 руб. соответственно. Фабрика должна ежедневно производить не менее двух столов. На производство другой продукции ограничений нет. Требуется определить, какую продукцию и в каком количестве следует ежедневно изготавливать фабрике, чтобы прибыль от ее реализации была максимальной.
Решение.
Составим вспомогательную таблицу:
| | Стол | Стул | Табурет | Ограничение ресурсов |
| Древесина, м3 | 1,5 | 1 | 0,62 | 12 |
| Рабочее время, маш.-час. | 5 | 1,5 | 0,7 | 26 |
| Прибыль за 1 шт., руб. | 200 | 30 | 15 | |
Определим переменные модели:
Используя эти переменные, далее строим целевую функцию:
Запишем ограничения:
Решение в Excel:
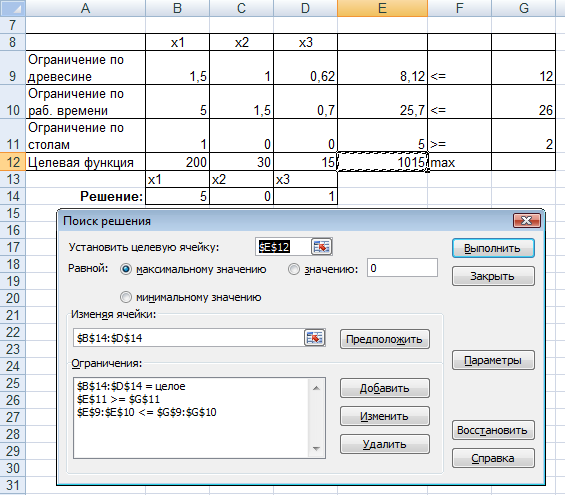

Рис. 2.4. Решение задачи целочисленного программирования