Добавлен: 11.01.2024
Просмотров: 122
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
решений содержит бесконечное число точек, необходима некая процедура поиска оптимального решения.
Нахождение оптимального решения требует определения направления возрастания целевой функции
(напомним, что мы максимизируем функцию z). Мы можем приравнять z к нескольким возрастающим значениям, например 10 и 15.
Эти значения, подставленные вместо z в выражение целевой функции, порождают уравнения прямых. Для значений 10 и 15 получаем уравнения прямых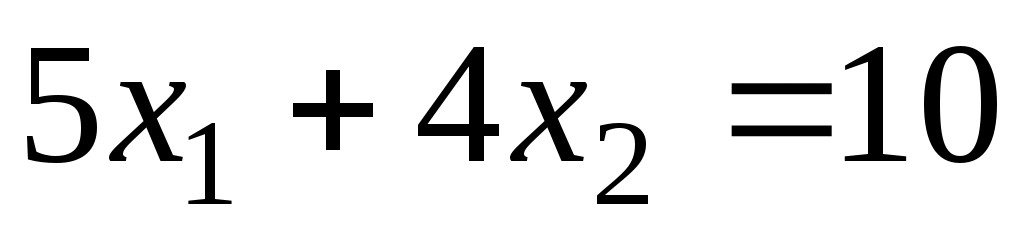
и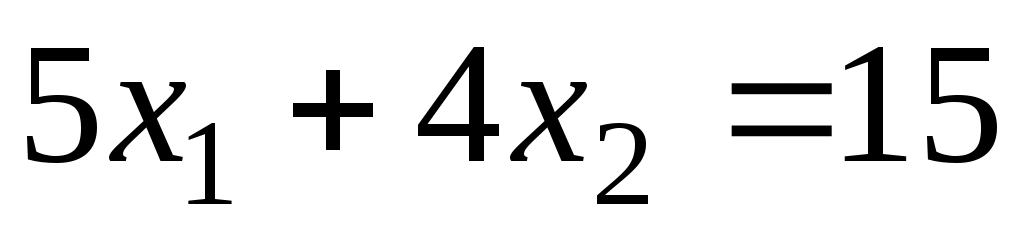 
. На рис. 2.2 эти прямые показаны штриховыми линиями, а направление возрастания целевой функции толстой стрелкой.
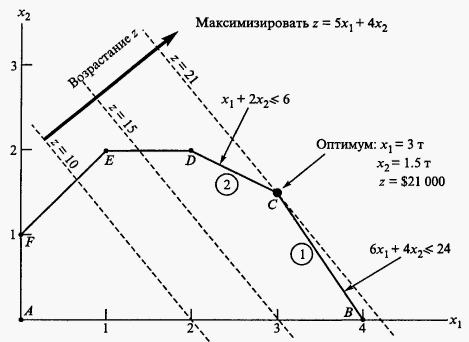
Рис. 2.2. Оптимальное решение модели
Целевая функция может возрастать до тех пор, пока прямые, соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.
На рис. 2.2 видно, что оптимальное решение соответствует точке С. Эта точка является местом пересечения прямых (1) и (2), поэтому ее координаты
и 
находятся как решение системы уравнений, задающих эти прямые:
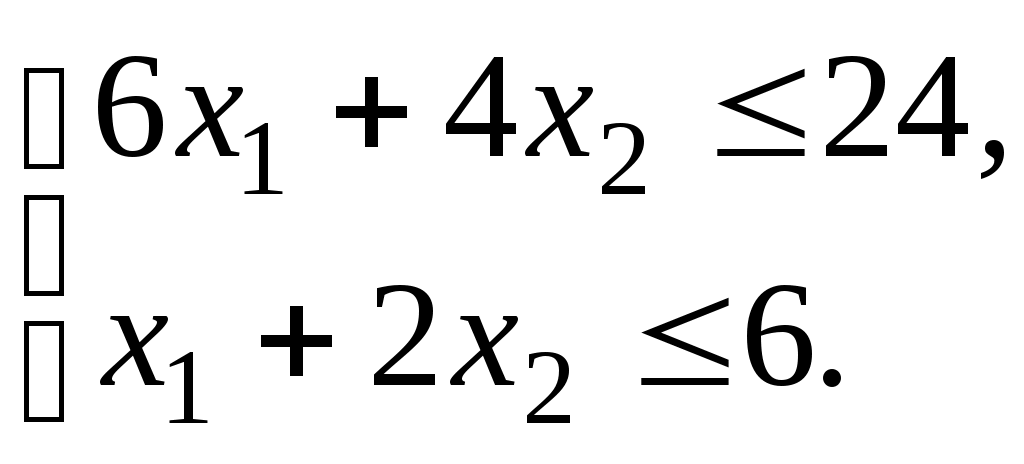
Решением этой системы будет
и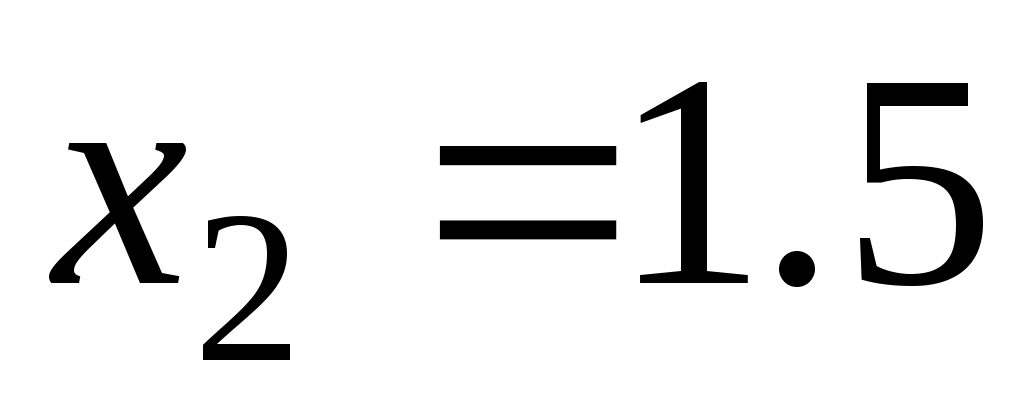 
, при этом значение целевой функции равно
.
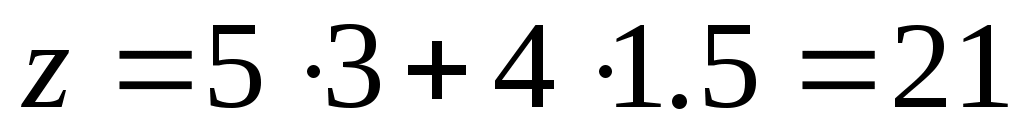Полученное решение означает, что для компании Mikks оптимальным выбором будет ежедневное производство 3 т краски для наружных работ и 1.5 т для внутренних работ с ежедневным доходом в $21 000.
Не случайно, что оптимальное решение расположено в угловой точке пространства допустимых решений, где пересекаются две прямые. Если мы изменим наклон функции z (путем изменения ее коэффициентов), то обнаружим, что в любом случае решение достигается в одной из угловых точек (или одновременно в нескольких угловых точках). В этом и состоит основная идея построения общего симплексного алгоритма, который будет рассмотрен далее.
Пример 2.2. Задача о диете
Фармацевтическая фирма Ozark ежедневно производит не менее 800 кг некой пищевой добавки – смеси кукурузной и соевой муки, состав которой представлен в следующей таблице.
Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма Ozark хочет определить рецептуру смеси минимальной стоимости с учетом требований диетологов.
Поскольку пищевая добавка состоит только из кукурузной и соевой муки, переменными для этой задачи, очевидно, будут
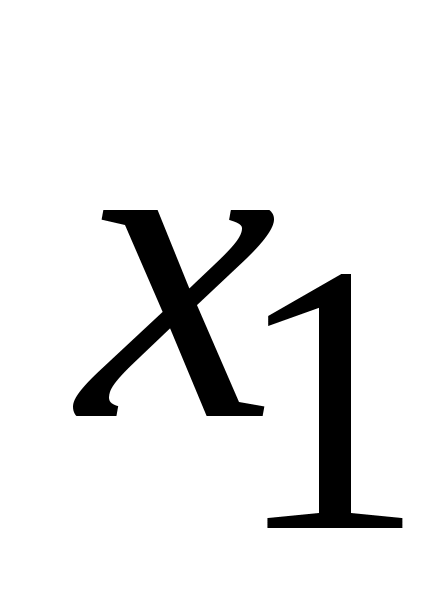количество (в кг) кукурузной муки, используемой в дневном производстве пищевой добавки;
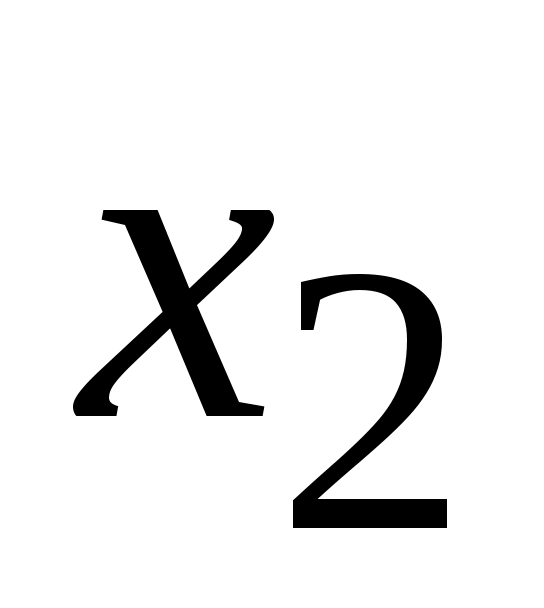количество (в кг) соевой муки, используемой в дневном производстве пищевой добавки.
Целевая функция равна общей стоимости пищевой добавки, производимой за один день, и должна быть минимальной. В данном случае это можно записать следующим образом:
Минимизировать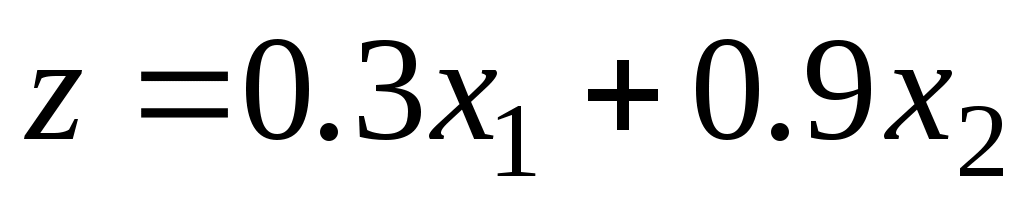
(или 
)
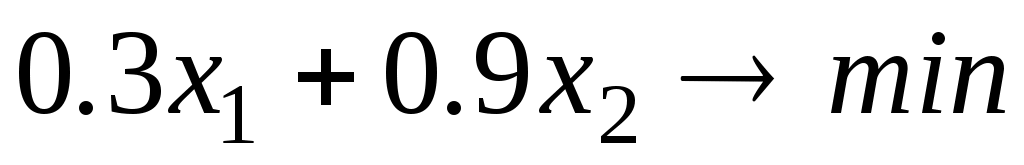Ограничения модели должны отражать производственные требования и рекомендации диетологов. Фирма должна выпускать не менее 800 кг смеси в день; соответствующее ограничение будет записано следующим образом:
.
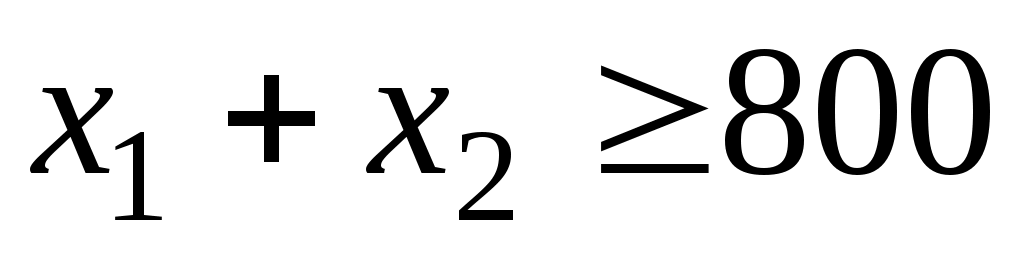Рассмотрим ограничение, связанное с количеством белка в пищевой добавке. Общее количество белка в смеси, состоящей из кг кукурузной муки и кг соевой муки, равно 
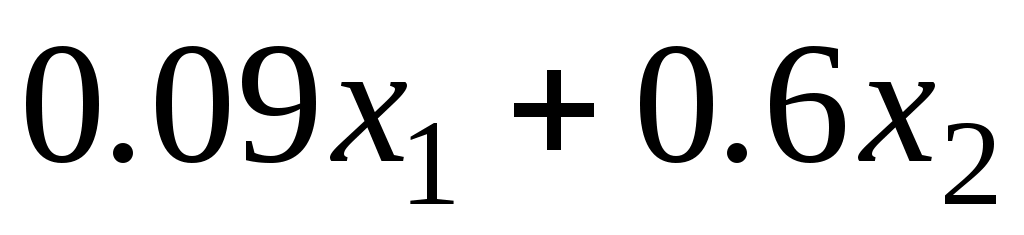(кг).
Это количество должно составлять не менее 30% от общего объема смеси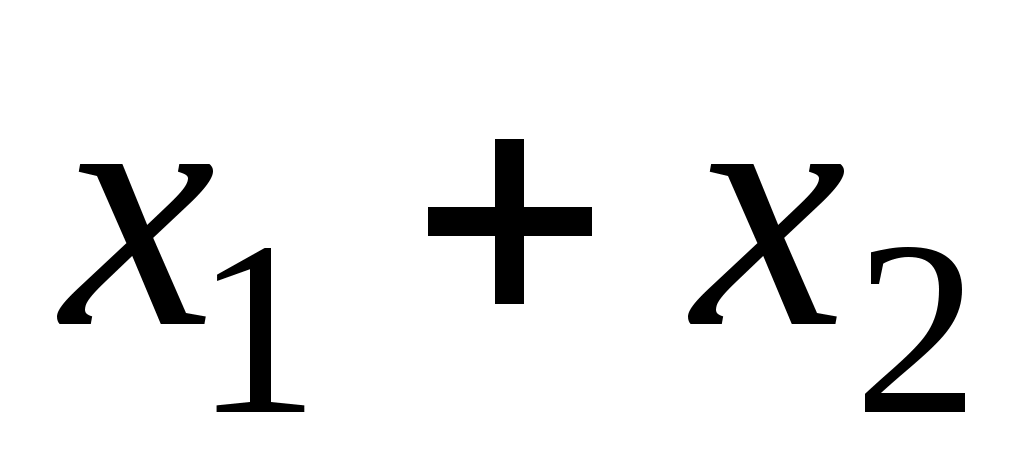
. Отсюда получаем следующее неравенство: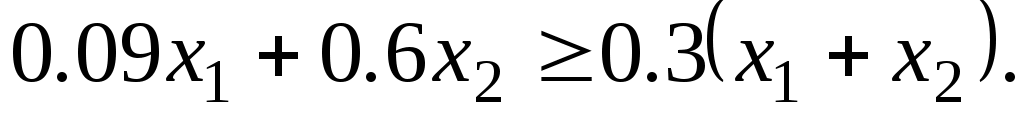 
Аналогично строится ограничение для клетчатки:
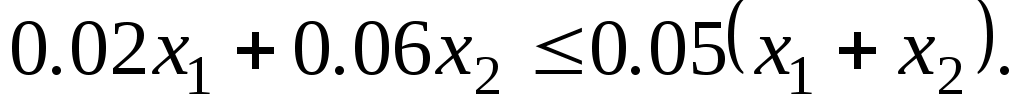
В последних двух неравенствах переменные
и 
надо перенести из правых частей в левые. Окончательно модель примет следующий вид.
Минимизировать
(или 
)
при ограничениях
, 
.
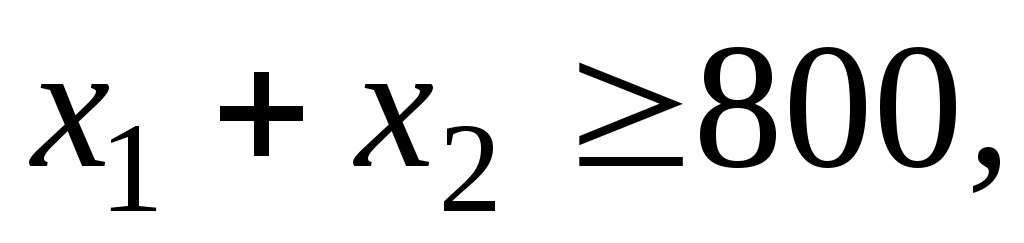
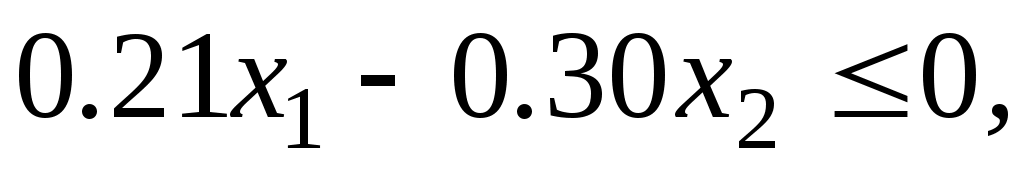
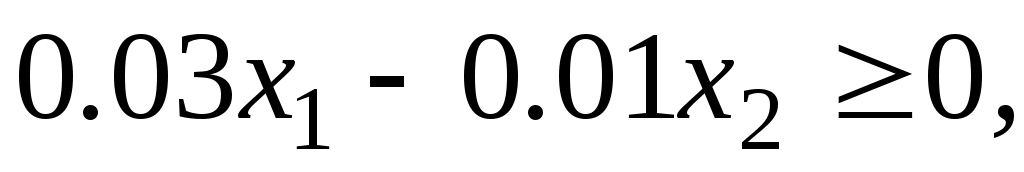
На рис. 2.3 показано графическое решение этой задачи.
Поскольку в данной модели следует минимизировать целевую функцию, поэтому нужно идти в направлении уменьшения ее значений (это направление на рис. 2.3 показано стрелкой). Оптимальное решение находится на пересечении прямых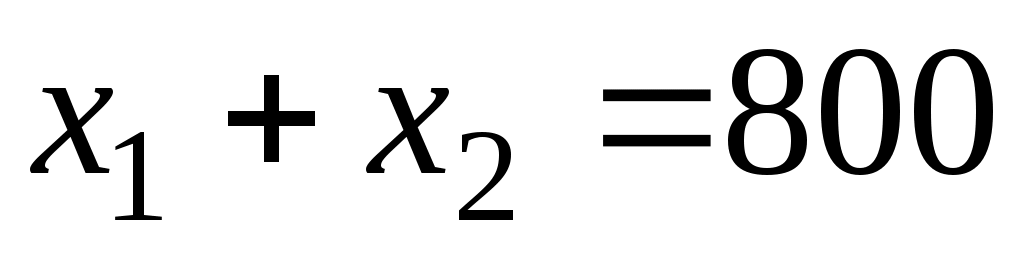
и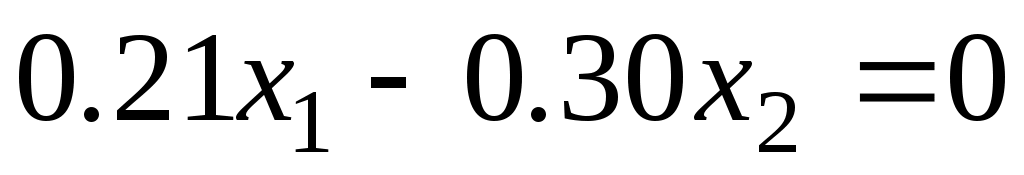 
, откуда получаем 
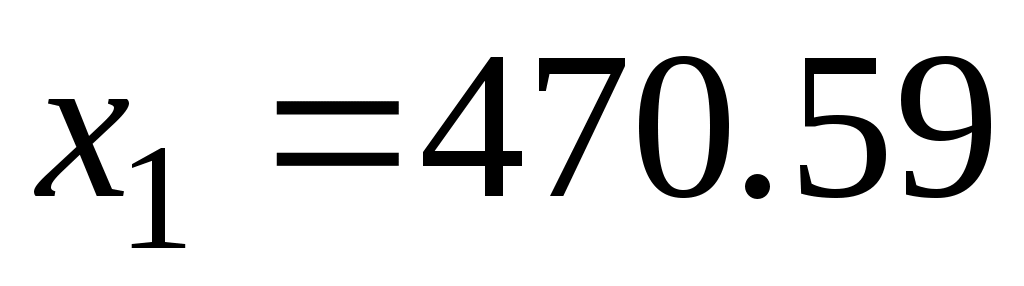(кг) и
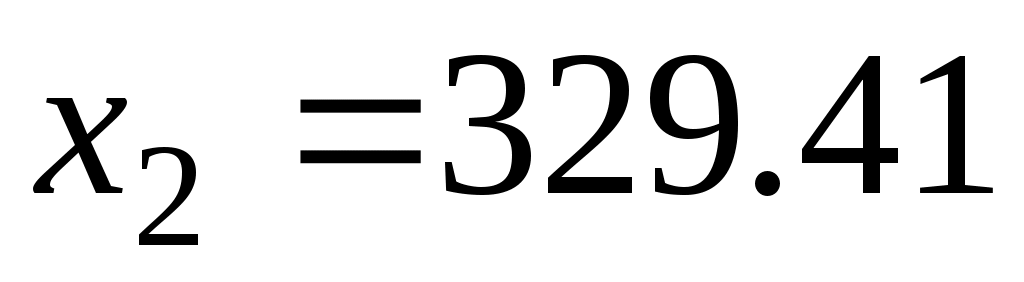(кг).
При этих значениях переменных минимальная стоимость производимой ежедневно пищевой добавки составляет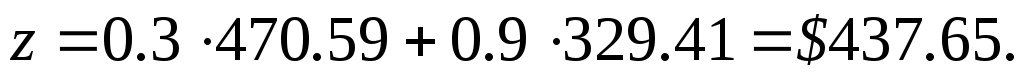
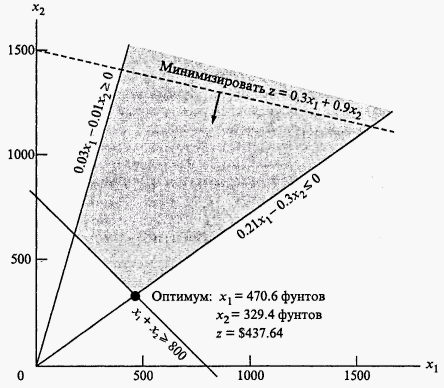
Рис. 2.3. Графическое решение задачи о диете
Проиллюстрируем на примере Mikks.
Составим в Excel следующую таблицу:
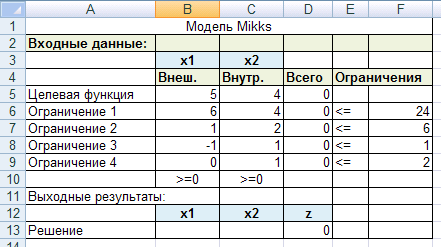
Здесь содержится 4 типа данных:
Для инструмента Поиск решения требуется информация только первых трех типов – поясняющие заголовки и надписи необходимы только для того, чтобы сделать табличное представление модели более понятным и удобочитаемым.
Покажем соответствие между математической моделью и табличной.
После ввода исходных данных и расчетных формул табличная модель готова для использования средства Поиск решения.
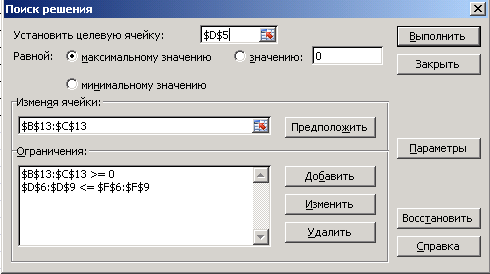
Откроется одноименное диалоговое окно:
Нахождение оптимального решения требует определения направления возрастания целевой функции
(напомним, что мы максимизируем функцию z). Мы можем приравнять z к нескольким возрастающим значениям, например 10 и 15. Эти значения, подставленные вместо z в выражение целевой функции, порождают уравнения прямых. Для значений 10 и 15 получаем уравнения прямых
и . На рис. 2.2 эти прямые показаны штриховыми линиями, а направление возрастания целевой функции толстой стрелкой. Рис. 2.2. Оптимальное решение модели
Целевая функция может возрастать до тех пор, пока прямые, соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.
На рис. 2.2 видно, что оптимальное решение соответствует точке С. Эта точка является местом пересечения прямых (1) и (2), поэтому ее координаты
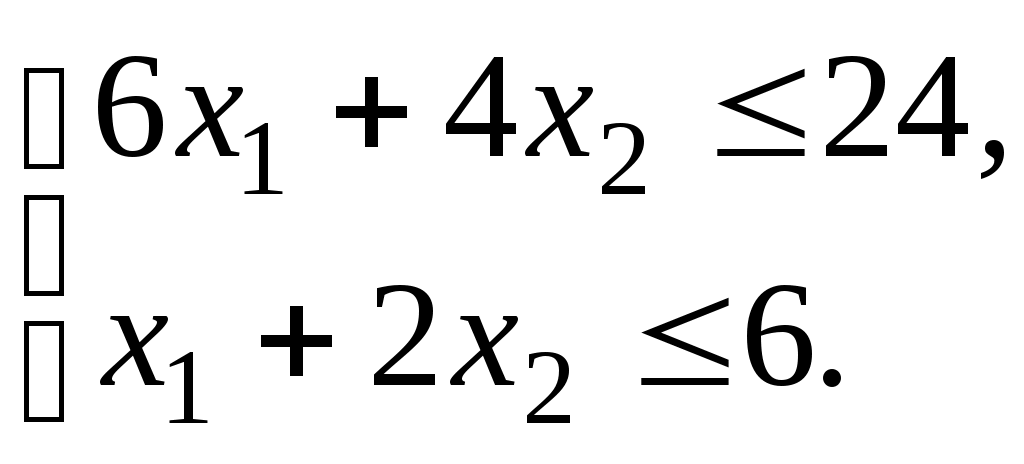
и находятся как решение системы уравнений, задающих эти прямые: Решением этой системы будет
и , при этом значение целевой функции равно . Полученное решение означает, что для компании Mikks оптимальным выбором будет ежедневное производство 3 т краски для наружных работ и 1.5 т для внутренних работ с ежедневным доходом в $21 000.
Не случайно, что оптимальное решение расположено в угловой точке пространства допустимых решений, где пересекаются две прямые. Если мы изменим наклон функции z (путем изменения ее коэффициентов), то обнаружим, что в любом случае решение достигается в одной из угловых точек (или одновременно в нескольких угловых точках). В этом и состоит основная идея построения общего симплексного алгоритма, который будет рассмотрен далее.
1.2.2.Нахождение минимума целевой функции
Пример 2.2. Задача о диете
Фармацевтическая фирма Ozark ежедневно производит не менее 800 кг некой пищевой добавки – смеси кукурузной и соевой муки, состав которой представлен в следующей таблице.
| Мука | Белок | Клетчатка | Стоимость (в $ за кг) |
| (в кг на кг муки) | |||
| Кукурузная | 0,09 | 0,02 | 0,30 |
| Соевая | 0,6 | 0,06 | 0,90 |
Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма Ozark хочет определить рецептуру смеси минимальной стоимости с учетом требований диетологов.
Поскольку пищевая добавка состоит только из кукурузной и соевой муки, переменными для этой задачи, очевидно, будут
количество (в кг) кукурузной муки, используемой в дневном производстве пищевой добавки; количество (в кг) соевой муки, используемой в дневном производстве пищевой добавки.Целевая функция равна общей стоимости пищевой добавки, производимой за один день, и должна быть минимальной. В данном случае это можно записать следующим образом:
Минимизировать
(или )Ограничения модели должны отражать производственные требования и рекомендации диетологов. Фирма должна выпускать не менее 800 кг смеси в день; соответствующее ограничение будет записано следующим образом:
.Рассмотрим ограничение, связанное с количеством белка в пищевой добавке. Общее количество белка в смеси, состоящей из
кг кукурузной муки и кг соевой муки, равно (кг). Это количество должно составлять не менее 30% от общего объема смеси
. Отсюда получаем следующее неравенство: Аналогично строится ограничение для клетчатки:
В последних двух неравенствах переменные
и надо перенести из правых частей в левые. Окончательно модель примет следующий вид.Минимизировать
(или )при ограничениях
, .На рис. 2.3 показано графическое решение этой задачи.
Поскольку в данной модели следует минимизировать целевую функцию, поэтому нужно идти в направлении уменьшения ее значений (это направление на рис. 2.3 показано стрелкой). Оптимальное решение находится на пересечении прямых
и , откуда получаем (кг) и
(кг). При этих значениях переменных минимальная стоимость производимой ежедневно пищевой добавки составляет
Рис. 2.3. Графическое решение задачи о диете
1.3.Компьютерное решение задач ЛП (при помощи Excel)
Проиллюстрируем на примере Mikks.
Составим в Excel следующую таблицу:
Здесь содержится 4 типа данных:
-
входные данные (ячейки B5:C9 и F6:F9), -
значения переменных и целевой функции (ячейки в прямоугольнике B13:D13), -
формулы, по которым вычисляются значения целевой функции и левых частей ограничений (ячейки D5:D9) и -
поясняющие заголовки и надписи.
Для инструмента Поиск решения требуется информация только первых трех типов – поясняющие заголовки и надписи необходимы только для того, чтобы сделать табличное представление модели более понятным и удобочитаемым.
Покажем соответствие между математической моделью и табличной.
| | Алгебраическая формула | Формула Excel | Ячейка |
| Целевая функция z |  | =B5*B$13+C5*C$13 | D5 |
| Ограничение 1 |  | =B6*B$13+C6*C$13 | D6 |
| Ограничение 2 |  | =B7*B$13+C7*C$13 | D7 |
| Ограничение 3 |  | =B8*B$13+C8*C$13 | D8 |
| Ограничение 4 | | =B9*B$13+C9*C$13 | D9 |
После ввода исходных данных и расчетных формул табличная модель готова для использования средства Поиск решения.
Откроется одноименное диалоговое окно: