Файл: 1. введение в линейное программирование.doc

Здесь дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.

Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц (СТ).

Базисные переменные			Свободные члены
	6	4	24
	1	2	6
	-1	1	1
	0	1	2
	-5	-4	0

Замечание. Если целевую функцию необходимо максимизировать, то предварительно нужно умножить ее на (–1).
Сформулируем алгоритм СМ применительно к данным, внесенным в таблице.

Шаг 1. Выяснить, имеются ли в последней строке таблицы отрицательные числа (значение в последнем столбце не принимается во внимание). Если все числа неотрицательны, то процесс закончен; базисное решение является оптимальным; .

Если в последней строке имеются отрицательные числа, перейти к Шагу 2.

Шаг 2.

---

Просмотреть столбец, соответствующий наименьшему отрицательному числу и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов нет положительных чисел, то оптимального решения не существует.

Если найден столбец, содержащий хотя бы один положительный элемент, отметить его и перейти к Шагу 3.

Шаг 3. Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку, соответствующую наименьшему частному (горизонтальной стрелкой). Выделить разрешающий элемент , стоящий на пересечении отмеченных строки и столбца. Перейти к Шагу 4.

Шаг 4.

1. 
   Поменять местами переменные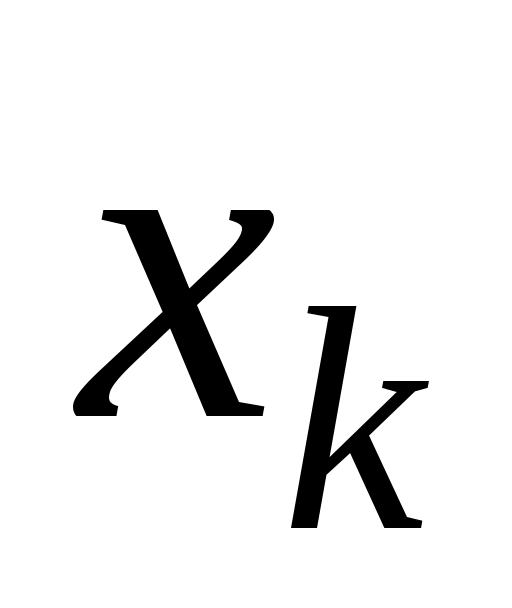 и , остальные переменные оставить на прежних местах.
   
2. 
   На место опорного элемента поставить число .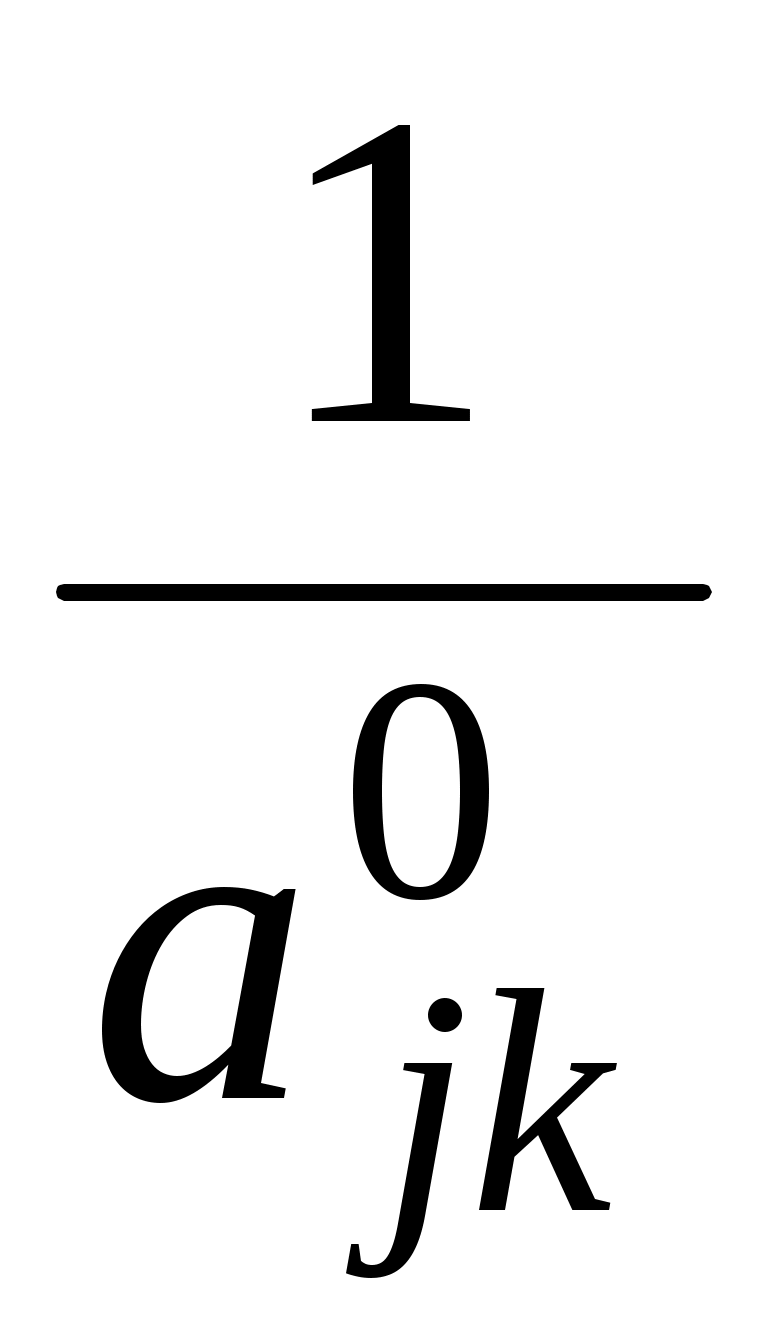
   
3. 
   На остальных местах разрешающей (опорной) строки записать соответствующие элементы исходной таблицы, делённые на опорный элемент.
   
4. 
   На свободные места разрешающего столбца поставить со знаком минус соответствующие элементы исходной таблицы, делённые на опорный элемент.
   

Шаг 5.

Оставшиеся свободные места в новой СТ заполнить построчно следующим образом: из строки элементов исходной таблицы вычесть произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы.

На этом заполнение новой таблицы заканчивается и происходит переход к Шагу 1.

Пример 2.5. Приведем ход решения задачи по данному алгоритму:

Базисные переменные			Свободные члены
	6	4	24
	1	2	6
	-1	1	1
	0	1	2
			0
Базисные переменные			Свободные члены
	0,17	0,67	4,00
	-0,17	1,33	2,00
	0,17	1,67	5,00
	0,00	1,00	2,00
	0,83	-0,67	20,00
Базисные переменные			Свободные члены
	0,25	-0,50	3,00
	-0,13	0,75	1,50
	0,38	-1,25	2,50
	0,13	-0,75	0,50
	0,75	0,50	21,00

---

Ответ:

---

1.7.Транспортная задача

Транспортная задача является особым типом задач целочисленного программирования, для которых разработаны простые и эффективные способы нахождения оптимального решения, не требующие громоздких вычислений. Экономико-математическую модель транспортной задачи рассмотрим на следующем примере.

Пример 2.6. Имеются три поставщика некоторого товара и четыре потребителя этого товара. Причём известна стоимость перевозки товара от каждого поставщика к каждому потребителю. Требуется найти объёмы перевозок для каждой пары "поставщик − потребитель" так, чтобы суммарные затраты на перевозку были минимальны, запасы всех поставщиков реализованы и потребности всех потребителей удовлетворены (табл.2.1).
Таблица 2.1.

Поставщики	Потребители								Запасы поставщиков,
	7		2		4		8		340
	8		9		6		5		200
	3		5		7		2		160
Спрос потребителей,	120		170		150		260

---

В левом верхнем углу произвольной клетки стоит коэффициент, равный стоимости перевозки от поставщика, номер которого указан в этой строке, к потребителю, номер которого указан в столбце.

В теории транспортной задачи таблица вида табл. 2.1 называется таблицей поставок.

Построим экономико-математическую модель данной задачи, обозначив через объем поставляемого товара от i -го поставщика к j- му потребителю. Чтобы запасы каждого поставщика были полностью реализованы, должны быть справедливы уравнения баланса для каждой строки таблицы поставок, т. е. выполняться равенства

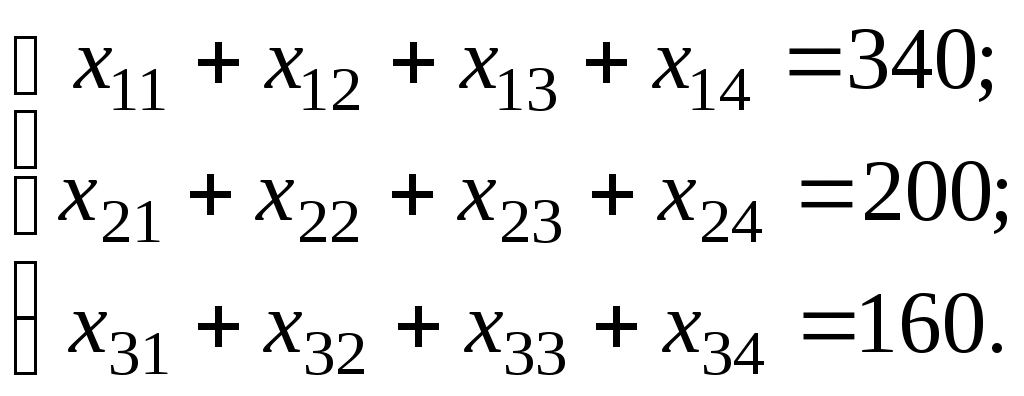(2.4)

Чтобы спрос каждого из потребителей был удовлетворён, должны быть справедливы уравнения баланса для каждого столбца таблицы поставок, то есть

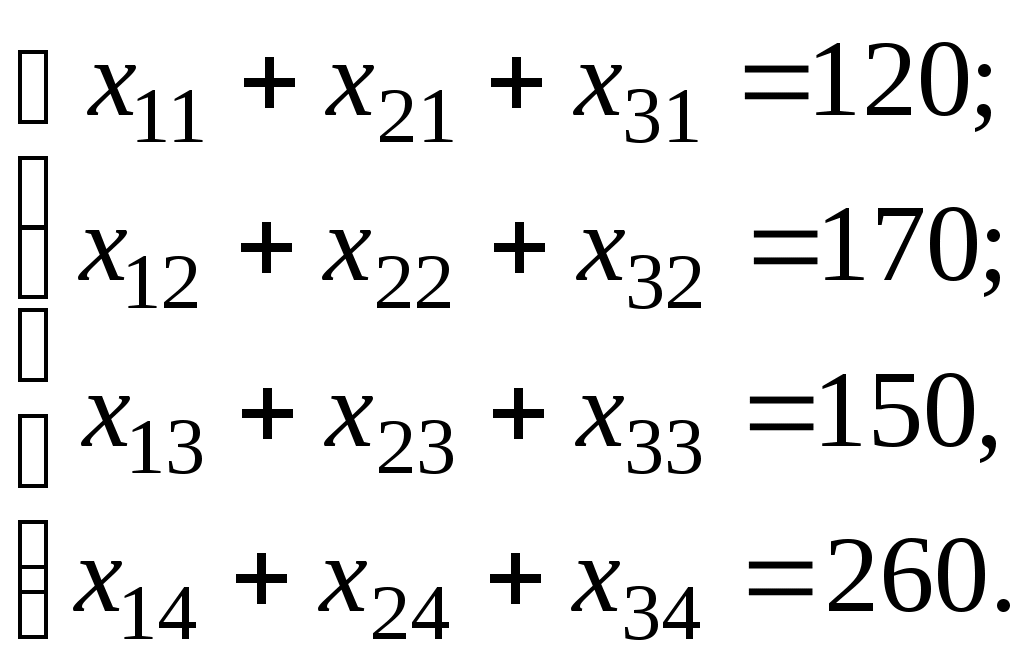(2.5)

Поскольку объём перевозимого груза величина неотрицательная, то должны выполняться ограничения на переменные :



Суммарные затраты F на перевозку определяются указанными в таблице поставок тарифами перевозок и размерами поставок:

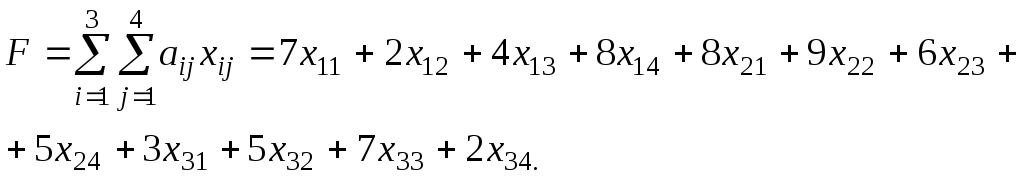(2.6)

Решить транспортную задачу − значит на множестве неотрицательных решений системы ограничений найти такое решение, при котором линейная функция принимает минимальное значение.

Транспортная задача называется закрытой (сбалансированной), если сумма запасов всех n поставщиков равна сумме потребностей всех m потребителей:



В противном случае транспортная задача называется открытой. Решение открытой транспортной задачи сводят к решению закрытой транспортной задачи введением фиктивных потребителей, когда сумма запасов превышает сумму потребностей, или фиктивных поставщиков, когда сумма потребностей превышает сумму запасов. При этом тарифы перевозок для фиктивных поставщиков и потребителей принимаются равными нулю.

Число основных (базисных) переменных закрытой транспортной задачи равно

---