ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 152
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
только переменные составляющие токов и напряжений. Согласно пер- вому закону Кирхгофа, ток в выходной цепи
iк = iL+iC+iR . (2)
С целью упрощения расчетов используем два допущения:
а) входной ток активного элемента считаем отсутствующим (iB = 0), что дос- тигается в генераторах на полевых транзисторах подачей надлежащего смеще- ния во входную цепь, тогда
к
u L diL dt
1 iсdt ir Rэ , (3)
dt
M u ; (4)
б) пренебрегаем влиянием выходного напряжения усилителя на ток iК, счи- тая его зависящим только от входного напряжения
iк = Ф(uв), (5)
что в большинстве случаев лишь несколько снижает точность расчетов, не вли- яя на характер получающихся зависимостей.
Выражение (5) можно рассматривать как аппроксимацию проходной ха- рактеристики активного элемента относительно рабочей точки. Производную
тока iк по времени запишем как
diк dt
diк
duв
duв dt
Suв duв , (6)
dt
где S(uв) = Ф'(uв) - крутизна характеристики (5). Заменяем токи в (2), согласно
(5) и (3):
1 u кdt C duк uк
Фu в .
о
Дифференцируя это уравнение по времени, используя (6) и (4) и обозна- чая ω2 =1/LC, получаем дифференциальное уравнение генератора:
d2uв 1
МSuв duв 2
. (7)
dt2
R
эC LC
dt
0uв 0
Это уравнение является нелинейным, поскольку коэффициент при duв/dt зави-
сит от искомой переменной uв. Нелинейность уравнения является следствием наличия в схеме нелинейного элемента. Уравнение определяет все свойства рассматриваемого генератора, его решение позволяет установить и условия са- мовозбуждения, и особенности стационарны их колебаний, и характер пере- ходных процессов.
При определении условий самовозбуждения колебаний нелинейное уравнение генератора (7), как уже отмечалось, может быть заменено линейным. Действительно, в этом случае нас только интересует, что будет с небольшим отклонением от состояния равновесия: станет оно затухать или нарастать. Так
как нелинейная функция S(uв), представляющая собой крутизну проходной ха-
рактеристики прямой передачи, не имеет разрыва, для малых величин uв она может быть заменена значением этой функции при uв=0, т.е. крутизной S(0)=S в рабочей точке. В результате нелинейное уравнение (7) превращается в линей- ное:
d2u 1
МSdu 2
. (8)
2 0u 0
dt RэC
LCdt
Здесь напряжение u записано без индекса, поскольку уравнение справедливо и для uK, в чем легко убедиться, используя (4). Уравнение (8) можно записать как уравнение контура
d2u
du 2
, (9)
dt2
2э dt 0u 0
2 R
где э 1 1
эС
МS- эквивалентный коэффициент затухания.
LC
Его решение имеет вид
u Ae э t
sin( C t
) ,
 где А и φ - амплитуда и фаза, зависящие от начальных условий; с
где А и φ - амплитуда и фаза, зависящие от начальных условий; с
2 2 -
0 э
частота свободных колебаний. Если записать RЭ = L/Cr, где r - сумма сопротив- лений потерь, включенных последовательно в ветвях контура, то
э 1 r МSMS , (10)
2 L LC 2LC
где α = r/2L = 1/2RЭС — коэффициент затухания контура.
Уравнение (9) показывает, что генератор эквивалентен колебательному контуру, коэффициент затухания которого уменьшен на величину MS/2LC, за- висящую от взаимоиндукции М, т.е. от обратной связи. Полученный результат означает, что переменное напряжение на входе активного элемента, благодаря
наличию обратной связи, создает ток iк, доставляющий в колебательную систе- му
энергию, компенсирующую потери в ней. Необходимая же энергия пере-
менного тока iк получается благодаря тому, что переменное напряжение uв управляет расходом энергии источника постоянного тока, имеющимся в вы- ходной цепи, т.е. благодаря преобразованию энергии постоянного тока в энер- гию переменного тока.
Если обратная связь невелика (αЭ > 0 или MS/C < r), вносимая энергия лишь частично компенсирует расходуемую в колебательной системе, поэтому возникшее колебание затухает, хотя и медленнее, чем в отсутствие обратной связи. При достаточно сильной обратной связи коэффициент αЭ оказывается отрицательным (вносимая энергия больше расходуемой) и колебания нара-
стают. Рассмотрим зависимость характера колебаний от αэ (рис. 3).
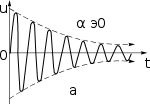
 uα э0
uα э0
0t
б
Рис.3
или
Условия самовозбуждения генератора можно записать как
αэ <0 (11)
M > MKP = L/SRЭ = rC/S. (12)
В рамках допущений, принятых при выводе уравнения генератора, коэф- фициент обратной связи Ко.с = М/L, а коэффициент усиления усилителя
Кy = SRэ. Поэтому условие самовозбуждения (12) идентично условию (1).
Обратная связь, способствующая самовозбуждению колебаний, называ- ется положительной. В рассмотренном случае она соответствует M>0. Если знак М изменить на обратный, для чего достаточно поменять местами точки подключения одной из обмоток трансформатора, то затухание контура возрас- тет и самовозбуждение станет невозможным. Обратная связь, затрудняющая самовозбуждение, т.е. увеличивающая устойчивость состояния равновесия, на- зывается отрицательной. Следовательно, для создания автогенераторов необхо- димо использование положительной обратной связи.
Точных аналитических методов решения нелинейных дифференциаль- ных уравнений (за редким исключением) не существует. В связи с этим было разработано большое количество разнообразных методов приближенного ана- лиза нелинейных цепей. Каждый метод обладает определенными пре- имуществами при решении круга задач. Наиболее распространенными метода- ми являются: метод линеаризации; квазилинейный метод (метод гармонической линеаризации); метод медленно меняющихся амплитуд; метод фазовой плоско- сти; метод малого параметра; метод математического моделирования.
Наибольшее распространение для инженерных расчетов стационарных режимов автогенераторов получил квазилинейный метод, основанный на ис- следовании соотношений между первыми гармониками токов и напряжений и замене нелинейною элемента эквивалентным линейным, характеризуемым средним по первой гармонике параметром. После такой замены нелинейная цепь описывается линейными уравнениями и может исследоваться методами линейной теории (например методом комплексных амплитуд). Квазилинейный метод применим для систем, колебания в которых близки к гармоническим.
Рассмотрим схему автогенератора (см. рис.1) с контуром в выходной цепи усилителя, активным элементом которого могут быть биполярный или полевой транзистор. Благодаря значительной добротности (обычно порядка 50 – 200) колебательные контуры генераторов обладают большой изби- рательностью. Поэтому даже тогда, когда выходной ток усилителя сильно от- личается от синусоидального из-за нелинейности АЭ, напряжения на контуре
uк и на входе АЭ uв оказываются почти синусоидальными, лишь незначительно
отличающимися от их первых гармоник uк1 , uв1. Анализируемый генератор со- стоит из двух частей: нелинейной (АЭ) и линейной (контура и катушки связи). Запишем соотношения между комплексными амплитудами первых гармоник токов и напряжений. Нелинейный элемент будем характеризовать средней кру- тизной, определяемой отношением комплексных амплитуд тока İК1 в выходной цепи АЭ к амплитуде напряжения возбуждения Ú
iк = iL+iC+iR . (2)
С целью упрощения расчетов используем два допущения:
а) входной ток активного элемента считаем отсутствующим (iB = 0), что дос- тигается в генераторах на полевых транзисторах подачей надлежащего смеще- ния во входную цепь, тогда
к
u L diL dt
1 iсdt ir Rэ , (3)
C
в
u M diL
dt
M u ; (4)
r
L
б) пренебрегаем влиянием выходного напряжения усилителя на ток iК, счи- тая его зависящим только от входного напряжения
iк = Ф(uв), (5)
что в большинстве случаев лишь несколько снижает точность расчетов, не вли- яя на характер получающихся зависимостей.
Выражение (5) можно рассматривать как аппроксимацию проходной ха- рактеристики активного элемента относительно рабочей точки. Производную
тока iк по времени запишем как
diк dt
diк
duв
duв dt
Suв duв , (6)
dt
где S(uв) = Ф'(uв) - крутизна характеристики (5). Заменяем токи в (2), согласно
(5) и (3):
1 u кdt C duк uк
Фu в .
L dt Rэ
о
Дифференцируя это уравнение по времени, используя (6) и (4) и обозна- чая ω2 =1/LC, получаем дифференциальное уравнение генератора:
d2uв 1
МSuв duв 2
. (7)
dt2
R
эC LC
dt
0uв 0
Это уравнение является нелинейным, поскольку коэффициент при duв/dt зави-
сит от искомой переменной uв. Нелинейность уравнения является следствием наличия в схеме нелинейного элемента. Уравнение определяет все свойства рассматриваемого генератора, его решение позволяет установить и условия са- мовозбуждения, и особенности стационарны их колебаний, и характер пере- ходных процессов.
При определении условий самовозбуждения колебаний нелинейное уравнение генератора (7), как уже отмечалось, может быть заменено линейным. Действительно, в этом случае нас только интересует, что будет с небольшим отклонением от состояния равновесия: станет оно затухать или нарастать. Так
как нелинейная функция S(uв), представляющая собой крутизну проходной ха-
рактеристики прямой передачи, не имеет разрыва, для малых величин uв она может быть заменена значением этой функции при uв=0, т.е. крутизной S(0)=S в рабочей точке. В результате нелинейное уравнение (7) превращается в линей- ное:
d2u 1
МSdu 2
. (8)
2 0u 0
dt RэC
LCdt
Здесь напряжение u записано без индекса, поскольку уравнение справедливо и для uK, в чем легко убедиться, используя (4). Уравнение (8) можно записать как уравнение контура
d2u
du 2
, (9)
dt2
2э dt 0u 0
2 R
где э 1 1
эС
МS- эквивалентный коэффициент затухания.
LC
Его решение имеет вид
u Ae э t
sin( C t
) ,
 где А и φ - амплитуда и фаза, зависящие от начальных условий; с
где А и φ - амплитуда и фаза, зависящие от начальных условий; с 2 2 -
0 э
частота свободных колебаний. Если записать RЭ = L/Cr, где r - сумма сопротив- лений потерь, включенных последовательно в ветвях контура, то
э 1 r МSMS , (10)
2 L LC 2LC
где α = r/2L = 1/2RЭС — коэффициент затухания контура.
Уравнение (9) показывает, что генератор эквивалентен колебательному контуру, коэффициент затухания которого уменьшен на величину MS/2LC, за- висящую от взаимоиндукции М, т.е. от обратной связи. Полученный результат означает, что переменное напряжение на входе активного элемента, благодаря
наличию обратной связи, создает ток iк, доставляющий в колебательную систе- му
энергию, компенсирующую потери в ней. Необходимая же энергия пере-
менного тока iк получается благодаря тому, что переменное напряжение uв управляет расходом энергии источника постоянного тока, имеющимся в вы- ходной цепи, т.е. благодаря преобразованию энергии постоянного тока в энер- гию переменного тока.
Если обратная связь невелика (αЭ > 0 или MS/C < r), вносимая энергия лишь частично компенсирует расходуемую в колебательной системе, поэтому возникшее колебание затухает, хотя и медленнее, чем в отсутствие обратной связи. При достаточно сильной обратной связи коэффициент αЭ оказывается отрицательным (вносимая энергия больше расходуемой) и колебания нара-
стают. Рассмотрим зависимость характера колебаний от αэ (рис. 3).

 uα э0
uα э00t
б
Рис.3
или
Условия самовозбуждения генератора можно записать как
αэ <0 (11)
M > MKP = L/SRЭ = rC/S. (12)
В рамках допущений, принятых при выводе уравнения генератора, коэф- фициент обратной связи Ко.с = М/L, а коэффициент усиления усилителя
Кy = SRэ. Поэтому условие самовозбуждения (12) идентично условию (1).
Обратная связь, способствующая самовозбуждению колебаний, называ- ется положительной. В рассмотренном случае она соответствует M>0. Если знак М изменить на обратный, для чего достаточно поменять местами точки подключения одной из обмоток трансформатора, то затухание контура возрас- тет и самовозбуждение станет невозможным. Обратная связь, затрудняющая самовозбуждение, т.е. увеличивающая устойчивость состояния равновесия, на- зывается отрицательной. Следовательно, для создания автогенераторов необхо- димо использование положительной обратной связи.
-
Стационарный режим автогенератора
Точных аналитических методов решения нелинейных дифференциаль- ных уравнений (за редким исключением) не существует. В связи с этим было разработано большое количество разнообразных методов приближенного ана- лиза нелинейных цепей. Каждый метод обладает определенными пре- имуществами при решении круга задач. Наиболее распространенными метода- ми являются: метод линеаризации; квазилинейный метод (метод гармонической линеаризации); метод медленно меняющихся амплитуд; метод фазовой плоско- сти; метод малого параметра; метод математического моделирования.
Наибольшее распространение для инженерных расчетов стационарных режимов автогенераторов получил квазилинейный метод, основанный на ис- следовании соотношений между первыми гармониками токов и напряжений и замене нелинейною элемента эквивалентным линейным, характеризуемым средним по первой гармонике параметром. После такой замены нелинейная цепь описывается линейными уравнениями и может исследоваться методами линейной теории (например методом комплексных амплитуд). Квазилинейный метод применим для систем, колебания в которых близки к гармоническим.
Рассмотрим схему автогенератора (см. рис.1) с контуром в выходной цепи усилителя, активным элементом которого могут быть биполярный или полевой транзистор. Благодаря значительной добротности (обычно порядка 50 – 200) колебательные контуры генераторов обладают большой изби- рательностью. Поэтому даже тогда, когда выходной ток усилителя сильно от- личается от синусоидального из-за нелинейности АЭ, напряжения на контуре
uк и на входе АЭ uв оказываются почти синусоидальными, лишь незначительно
отличающимися от их первых гармоник uк1 , uв1. Анализируемый генератор со- стоит из двух частей: нелинейной (АЭ) и линейной (контура и катушки связи). Запишем соотношения между комплексными амплитудами первых гармоник токов и напряжений. Нелинейный элемент будем характеризовать средней кру- тизной, определяемой отношением комплексных амплитуд тока İК1 в выходной цепи АЭ к амплитуде напряжения возбуждения Ú