ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 160
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
IK1
0Uв1Uв2U'
Uв10
0>
1 2 3 4 5 6
M M =M
M3MМ
в112кр 4
а б
Рис.7
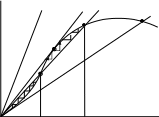
На этой же схеме приведены характеристики обратной связи для различ- ных значений М: М1<М2<М3<М4. Стационарным режимам соответствуют точки пересечения колебательной характеристики и характеристики обратной связи. При М=М3 точек пересечения окажется две: точка О, соответствующая состоя- нию равновесия UB1=0, и точка А3, соответствующая динамическому режиму с амплитудой U'B1. В каждой из них выполняется условие баланса амплитуд. Од- нако это еще не означает, что любой из этих режимов может быть получен. В реальных схемах может быть получен только устойчивый режим.
Для проверки устойчивости состояния равновесия (точки О) предполо- жим, что за счет какого-то возмущения возникло колебание напряжения с не- большой амплитудой ∆UB1. Это вызовет появление тока с амплитудой ∆IK1, оп- ределяемой по колебательной характеристике. В свою очередь, этот ток создает напряжение на входе АЭ с амплитудой ∆UB2, определяемой по характеристике обратной связи, причем ∆UB2>∆UB1, что вызовет дальнейшее увеличение тока и т. д. В итоге амплитуда случайно возникшего колебания возрастает, т.е. состоя- ние равновесия оказывается неустойчивым. Аналогично производится проверка устойчивости тока А3 путем введения предположения о случайном отклонении амплитуды UB1 от U'B1 в сторону больших и меньших значений. При этом легко убедиться, что динамический режим, соответствующий точке А3, является ус- тойчивым, так как небольшие отклонения затухают.
Стационарный режим я вляется устойчивым, если в точке пересечения характеристик крутизна колебательной характери- стики меньше крутизны характеристики обратной связи, и не- устойчивым в противоположном случае. Применение этого критерия к точкам О и A3 подтверждает сделанный ранее вывод о неустойчивости состояния рав- новесия и устойчивости динамического режима.
Графики (рис. 7, б) позволяют установить зависимость амплитуды колеба- ний, например IK1, от изменения M, определяющей величину обратной связи. При увеличении М от нуля до М2 = МKP единственным стационарным и притом устой- чивым режимом является состояние равновесия. При М>М2 появляются два ста- ционарных режима, причем устойчивым оказывается динамический режим (точки А3 и А4). Поэтому при М>М2 с ростом М амплитуда IK1 плавно изменяется (см. рис. 7,б). При уменьшении М амплитуда IK1 изменяется в соответствии с той же характеристикой, и при М2 = МKP колебания исчезают.
Режим генератора, в котором амплитуда колебании плавно меняется с изменением об ратной свя зи, называется м ягким ре - жим ом самовозб уждения колебаний.
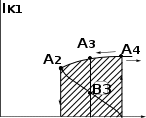
Жесткий режим. Рассмотрим колебательную характеристику и семейст- во характеристик обратной связи для различных значений М (М1<М2<М3<М4) (рис. 8,а). При М = М3 характеристики пересекаются в трех точках, соответст- вующих трем стационарным режимам: О - состоянию равновесия, В3 и А3 - ди- намическим режимам с амплитудами U''B1 и U'B1. Рассматривая процесс изме- нения IK1 и UB1 при небольших начальных отклонениях ∆UB1 от значений UB1, соответствующих точкам О, В3 и A3, убеждаемся в том, что точки О и A3 соот- ветствуют устойчивым, а точка В3 - неустойчивому режимам.
 IK1M1
IK1M1M2M3
M
4
 Ошибка!
Ошибка! A2A3A4
1 2 3 4 5 6
B3
U
в1
0Uв"1'
а
Uв10M1
Рис.8
M 2 M3 M 4 M M
 б
б
Определим зависимость амплитуды IK1 от величины обратной связи. При увеличении М от нуля до значения М = М4, при котором характеристики оказы- ваются касательными в начале координат, режим, соответствующий точке О, является устойчивым и малые флуктуации не вызывают нарастания колебаний. При М = М4 режим, соответствующий точке О, становится неустойчивым и ма- лые колебания сразу нарастают до больших амплитуд, соответствующих точке A4. При дальнейшем увеличении М изменение амплитуд происходит по колеба- тельной характеристике. Если теперь уменьшать М до М = М2, то при М = М4,
так же как и при М = М3, срыва колебаний не произойдет, так как динамические режимы, определяемые точками А3 и A4, являются устойчивыми. Колебания сорвутся, когда М уменьшится до М = М2, так как соответствующая ему точка А2 неустойчива: небольшое уменьшение амплитуды UB1 вызовет ее дальнейшее уменьшение до нуля. Зависимость IK1 от М для жесткого режима построена на схеме (см. рис. 8, б): сплошным линиям соответствуют устойчивые режимы, пунктирной - неустойчивые.
Жесткий режим самовозб уждения колебаний характеризу- ется скачкообразным возникновением колебаний б ольшой ам - плитуды при