ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 158
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
B1 на входе АЭ:
S& сp I&К1/UВ1 . (13)
Вследствие нелинейности АЭ S& ср
зависит от амплитуды
U& B1 . Пренебрегая
влиянием напряжения ÚК1 на ток İК1, получим из (13)
I&К1 S& срUВ1 . (14)
Если первая гармоника тока iK1 совпадает по фазе с первой гармоникой
напряжения возбуждения uB1 , средняя крутизна оказывается действительной. Однако на практике при работе на достаточно высоких частотах в результате конечного времени прохождения носителей через прибор ток iK1 отстает по фа- зе от uB1. Поэтому в общем случае среднюю крутизну (13) следует считать ком- плексной.
Для линейной части схемы (см. рис. 1) при iB1=0 имеем ÚK1= İ К1ZЭ и
Uв1 K& о.с.Uк1 K& о.с.ZэI&к1 причем комплексный коэффициент обратной связи
(15)
К& О.С. .=ÚB1 /ÚК1=M/L=KО.С.
оказывается действительным. Произведение КО.СZЭ, характеризующее линей- ную часть схемы, называют управляющим сопротивлением:
ZУ = КО.СZЭ. (16)
Подставляя (14) в (15), получим комплексное уравнение генератора:
S& срК& о.с.Zэ
1.
(17)
Оно имеет очевидный физический смысл: в стационарном режиме ком плексный коэффициент передачи по замкнутому контуру ге- нератора равен единице. Если воспользоваться (16), придем к иной форме комплексного уравнения генератора:
S& СР ZУ 1.
(18)
Представляя каждую из комплексных величин в показательной форме
S& ср
Sсреis ,
K& о.с. Kо.с.eiк ,
Zэ Zэeiк , (19)
можем записать уравнение (17) в виде
SсрKо.с.Zэei(s к z )
1. (20)
Уравнение (20) имеет место, если одновременно выполняются два условия:
s к z
0,2π,…, 2πn (21)
SсрKо.с.Zэ 1
(22)
Соотношения (21), (22) являются важнейшими в теории автогенераторов, определяющими параметры стационарного режима. Выражение (21), называе- мое условием баланса фаз, означает, что в стационарном режиме сумма всех
фазовых сдвигов по замкнутому контуру генератора равна нулю или целому числу 2π. Поскольку каждый из сдвигов фаз, входящих в это выражение, зави- сит от частоты по-разному, в большинстве генераторов существует лишь одна частота ω0, на которой выполняется условие баланса фаз, т.е. на которой возможно генерирование колеб аний. Таким образом, из условия балан- са фаз определяется частота генерируемых колебаний.
Выражение (22), называемое условием баланса амплитуд, говорит о том, что в стационарном режиме коэффициент передачи по замкнутому контуру ге-
нератора равен единице. В этом условии две величины (Ко.с и Zэ) от амплитуды
колебаний не зависят, а одна (Scp) зависит от UB1. Следовательно, условие ба- ланса амплитуд выполняется лишь при определенной амплитуде UB1. Для опре- деления амплитуды стационарных колебаний удобно (22) переписать в виде
Sср(UB1) = 1/Ко.с.Zэ. (23)
Рассмотрим (рис. 4) построенные зависимость Scp(UB1), называемую характеристикой средней крутизны, и прямую обратной связи, проведенную на
уровне 1/Ко.сZэ. Точка пересечения этих зависимостей определяет стационар- ную амплитуду колебаний ƯB1, для которой выполняется условие баланса ам- плитуд. Если частота генерируемых колебаний равна резонансной частоте кон- тура, то Zэ=Rэ и условие баланса амплитуд
Sср(UB1) = 1/Ко.сRэ. (24)
Scp
0U'В1UВ1
 Рис.4
Рис.4
Стационарный режим будет устойчивым, если большая
амплитуда UВ1 станет затухать, т.е. если при UВ1>U'В1 величина αЭ окажется положительной. Для этого требуется, чтобы
∂SCP/∂UВ1<0. (25)
Таким образом, стационарный режим автоколебаний я вля - ется устойчивым, если производ ная средней крутизны по ампли- туде напряжения отрицательна.
В квазилинейном методе для определения амплитуды стационарных ко- лебаний применяется также подход, основанный на использовании колебатель- ных характеристик.
Колебательной характеристикой называется зависимость амплитуды IK1 первой гармоники выходного тока нелинейного элемента от амплитуды UB входного гармонического напряжения:
IK1 = Ф1(UB). (26)
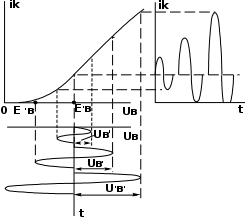 Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).
Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).
Рис.5
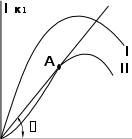
Если смещение Е''B соответствует нижнему загибу характеристики iK(uВ), то с увеличением UB сначала IK1 растет быстрее UB, а затем приблизительно пропорционально UB, что приводит к колебательной характеристике II. При больших амплитудах UB амплитуды IK1 всегда уменьшаются из-за влияния на- пряжения на нагрузке.
При любой амплитуде UB средняя крутизна
Scp = tgα, (27)
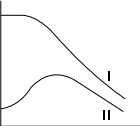
где α - угол наклона линии, соединяющей точку колебательной характеристики с началом координат. Рассмотрим характеристики средней крутизны S
cp(UB), соответствующие колебательным (I и II) (рис. 6, б). При малых UB Scp опреде- ляется крутизной S в рабочей точке Sср(0)=S.
Режим работы генератора с характеристиками I называется мягким, а с
характеристиками II - жестким. Отметим, что при характеристике II наиболь-
шее значение Scp соответствует точке А (см. рис. 6,а), в которой касательная к колебательной характеристике проходит через начало координат.
 Scp
Scp
0aUв 0
бUв
Рис.6
Следует отметить, что при анализе работы генератора в мяг- ком режиме вольт- амперная характеристика его нелинейного элемента должна быть аппроксимирована полиномом не ниже третьей степени, а в жестком – не ниже пя той степени.
Рассмотрим особенности каждого режима.
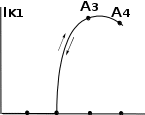
Мягкий режим. Помимо колебательной характеристики IK1 = Ф(UВ1) на схеме (рис. 7, а) построено семейство характеристик обратной связи, опреде- ляющих зависимость UВ1 от IK1 через линейные элементы генератора. Эти ха- рактеристики будут соответствовать выражению (15), если в последнем заме- нить комплексные амплитуды на модули: UB1 = Kо.сZэIк1. Решая это уравнение
относительно IK1 и учитывая, что Kо.с = M/L, получаем уравнение характери- стик обратной связи:
IK1 = (L/MZэ)UB1. (28)
IK1
M1M2M3M4

 A3A4
A3A4
S& сp I&К1/UВ1 . (13)
Вследствие нелинейности АЭ S& ср
зависит от амплитуды
U& B1 . Пренебрегая
влиянием напряжения ÚК1 на ток İК1, получим из (13)
I&К1 S& срUВ1 . (14)
Если первая гармоника тока iK1 совпадает по фазе с первой гармоникой
напряжения возбуждения uB1 , средняя крутизна оказывается действительной. Однако на практике при работе на достаточно высоких частотах в результате конечного времени прохождения носителей через прибор ток iK1 отстает по фа- зе от uB1. Поэтому в общем случае среднюю крутизну (13) следует считать ком- плексной.
Для линейной части схемы (см. рис. 1) при iB1=0 имеем ÚK1= İ К1ZЭ и
Uв1 K& о.с.Uк1 K& о.с.ZэI&к1 причем комплексный коэффициент обратной связи
(15)
К& О.С. .=ÚB1 /ÚК1=M/L=KО.С.
оказывается действительным. Произведение КО.СZЭ, характеризующее линей- ную часть схемы, называют управляющим сопротивлением:
ZУ = КО.СZЭ. (16)
Подставляя (14) в (15), получим комплексное уравнение генератора:
S& срК& о.с.Zэ
1.
(17)
Оно имеет очевидный физический смысл: в стационарном режиме ком плексный коэффициент передачи по замкнутому контуру ге- нератора равен единице. Если воспользоваться (16), придем к иной форме комплексного уравнения генератора:
S& СР ZУ 1.
(18)
Представляя каждую из комплексных величин в показательной форме
S& ср
Sсреis ,
K& о.с. Kо.с.eiк ,
Zэ Zэeiк , (19)
можем записать уравнение (17) в виде
SсрKо.с.Zэei(s к z )
1. (20)
Уравнение (20) имеет место, если одновременно выполняются два условия:
s к z
0,2π,…, 2πn (21)
SсрKо.с.Zэ 1
(22)
Соотношения (21), (22) являются важнейшими в теории автогенераторов, определяющими параметры стационарного режима. Выражение (21), называе- мое условием баланса фаз, означает, что в стационарном режиме сумма всех
фазовых сдвигов по замкнутому контуру генератора равна нулю или целому числу 2π. Поскольку каждый из сдвигов фаз, входящих в это выражение, зави- сит от частоты по-разному, в большинстве генераторов существует лишь одна частота ω0, на которой выполняется условие баланса фаз, т.е. на которой возможно генерирование колеб аний. Таким образом, из условия балан- са фаз определяется частота генерируемых колебаний.
Выражение (22), называемое условием баланса амплитуд, говорит о том, что в стационарном режиме коэффициент передачи по замкнутому контуру ге-
нератора равен единице. В этом условии две величины (Ко.с и Zэ) от амплитуды
колебаний не зависят, а одна (Scp) зависит от UB1. Следовательно, условие ба- ланса амплитуд выполняется лишь при определенной амплитуде UB1. Для опре- деления амплитуды стационарных колебаний удобно (22) переписать в виде
Sср(UB1) = 1/Ко.с.Zэ. (23)
Рассмотрим (рис. 4) построенные зависимость Scp(UB1), называемую характеристикой средней крутизны, и прямую обратной связи, проведенную на
уровне 1/Ко.сZэ. Точка пересечения этих зависимостей определяет стационар- ную амплитуду колебаний ƯB1, для которой выполняется условие баланса ам- плитуд. Если частота генерируемых колебаний равна резонансной частоте кон- тура, то Zэ=Rэ и условие баланса амплитуд
Sср(UB1) = 1/Ко.сRэ. (24)
| Scp (UВ1) | | |
| 1 Кос Zэ | | |
Scp

0U'В1UВ1
Стационарный режим будет устойчивым, если большая
амплитуда UВ1 станет затухать, т.е. если при UВ1>U'В1 величина αЭ окажется положительной. Для этого требуется, чтобы
∂SCP/∂UВ1<0. (25)
Таким образом, стационарный режим автоколебаний я вля - ется устойчивым, если производ ная средней крутизны по ампли- туде напряжения отрицательна.
-
Режимы возбуждения колебаний в автогенераторе
В квазилинейном методе для определения амплитуды стационарных ко- лебаний применяется также подход, основанный на использовании колебатель- ных характеристик.
Колебательной характеристикой называется зависимость амплитуды IK1 первой гармоники выходного тока нелинейного элемента от амплитуды UB входного гармонического напряжения:
IK1 = Ф1(UB). (26)
 Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).
Колебательная характеристика определяется по динамической вольт- амперной характеристике прибора (рис. 5): при выбранном смещении ЕВ для различных амплитуд входного напряжения (U'''B>U''B>U'B) строим графики тока iK и рассчитываем амплитуды их первых гармоник IK1. Для смещения Е'B, соот- ветствующего участку с постоянной крутизной S, при небольших амплитудах UB IK1=SUB. По мере увеличения UB напряжение все больше заходит на участки меньшей крутизны, в результате чего рост амплитуды IK1 замедляется (рис. 6,а).Рис.5
Если смещение Е''B соответствует нижнему загибу характеристики iK(uВ), то с увеличением UB сначала IK1 растет быстрее UB, а затем приблизительно пропорционально UB, что приводит к колебательной характеристике II. При больших амплитудах UB амплитуды IK1 всегда уменьшаются из-за влияния на- пряжения на нагрузке.
При любой амплитуде UB средняя крутизна
Scp = tgα, (27)
где α - угол наклона линии, соединяющей точку колебательной характеристики с началом координат. Рассмотрим характеристики средней крутизны S
cp(UB), соответствующие колебательным (I и II) (рис. 6, б). При малых UB Scp опреде- ляется крутизной S в рабочей точке Sср(0)=S.
Режим работы генератора с характеристиками I называется мягким, а с
характеристиками II - жестким. Отметим, что при характеристике II наиболь-
шее значение Scp соответствует точке А (см. рис. 6,а), в которой касательная к колебательной характеристике проходит через начало координат.

 Scp
Scp0aUв 0
бUв
Рис.6
Следует отметить, что при анализе работы генератора в мяг- ком режиме вольт- амперная характеристика его нелинейного элемента должна быть аппроксимирована полиномом не ниже третьей степени, а в жестком – не ниже пя той степени.
Рассмотрим особенности каждого режима.
Мягкий режим. Помимо колебательной характеристики IK1 = Ф(UВ1) на схеме (рис. 7, а) построено семейство характеристик обратной связи, опреде- ляющих зависимость UВ1 от IK1 через линейные элементы генератора. Эти ха- рактеристики будут соответствовать выражению (15), если в последнем заме- нить комплексные амплитуды на модули: UB1 = Kо.сZэIк1. Решая это уравнение
относительно IK1 и учитывая, что Kо.с = M/L, получаем уравнение характери- стик обратной связи:
IK1 = (L/MZэ)UB1. (28)
IK1
M1M2M3M4

 A3A4
A3A4