ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 310
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 5.6.9
| | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 1,00 | 1,00 | 0,00 | 0,00 | 0,00 |
| 2 | | 0 | 1,00 | 0,00 | 0,00 | 0,00 |
| 3 | | | 0 | 0,00 | 0,00 | 0,00 |
| 4 | | | | 0 | 1,00 | 1,00 |
| 5 | | | | | 0 | 1,00 |
| 6 | | | | | | 0 |
Подсчитаем сумму расстояний между объектами:
0+ 4+ 4+ 12+ 14+ 17+0+ 0+ 4+ 12+ 14+ 17+
0+ 0+ 0+ 8+ 10+ 13+
0+ 0+ 0+ 0+ 2+ 5+
0+ 0+ 0+ 0+ 0+ 3 =139.
Среднее расстояние = 139/15=9,27.
Сумма расстояний между объектами, вошедшими в кластеры:
1∙4+1∙4+1∙4+1∙2+1∙5+1∙3=22.Среднее расстояние между объектами в кластерах = 22/6=3,67.
Сумма расстояний между объектами, находящимися в разных кластерах:
(1-0)∙12+(1-0)∙14+(1-0)∙17++(1-0)∙12+(1-0)∙14+(1-0)∙17+
+(1-0)∙8+(1-0)∙10+(1-0)∙13= 117.
Среднее расстояние между объектами, находящимися в разных кластерах
=117/9=13.
Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 9,27/3,67=2,52; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 13/9,27=1,4.
Рассмотренные шесть примеров наглядно продемонстрировли методику применения основных методов кластерного анализа. Получение одинаковых результатов по всем рассмотренным методам объясняется сравнительной несложностью рассматриваемого примера. При усложнении примера следует ожидать различий в результатах кластерного анализа.
Задание 1.6
Пример 6.1
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах методом скользящего среднего с шагом m=3 числа. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
| Год | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Число ПК | 4150,5 | 4558,3 | 5709,6 | 6684,0 | 7528,4 | 8267,3 | 8743,7 | 9288,1 |
Вычислим сглаженные значения числа ПК:
Вычислим цепной годовой прирост:
Вычислим спрогнозированные значения числа ПК для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
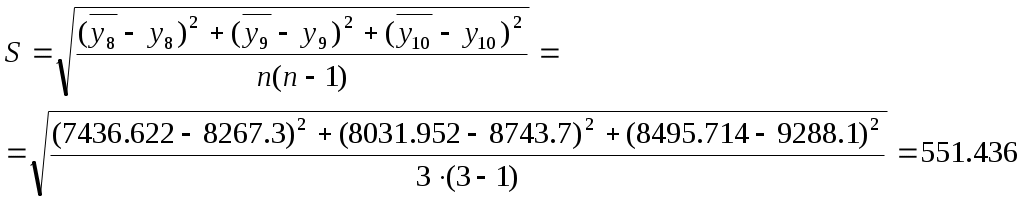
Вычислим отношение ошибки к среднему значению:
Так как отношение среднеквадратической ошибки к среднему значению превышает рекомендуемое значение 0.05 сравнительно на немного, то резуль-тат признаем допустимым.
Полученные результаты сглаживания и прогнозирования.
| Год | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Число ПК | 4150,5 | 4558,3 | 5709,6 | 6684,0 | 7528,4 | 8267,3 | 8743,7 | 9288,1 |
| Число ПК: сглаженное, спрогнозир. | 4026.6 | 4806.1 | 5650.6 | 6640.7 | 7485.1 | 7436.6 | 8032.0 | 8495.7 |
Спрогнозируем количество ПК в 2011, 2012, 2013 годах.
Вычислим спрогнозированные значения числа ПК для оценки качества:
Полученные результаты сглаживания и прогнозирования.
| Год | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Число ПК | 8267,3 | 8743,7 | 9288,1 | - | - | - |
| Число ПК: спрогнозированное | 7436.6 | 8032.0 | 8495.7 | 8832.6 | 9297.9 | 9719.9 |
На рис.6.1 результаты сглаживания и прогнозирования представлены в графическом виде.
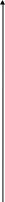
у
11
10
9
Экспериментальные значения 
8 
Спрогнозированные значения 
7 
6 
Сглаженные значения
5
4 
3 4 5 6 7 8 9 10 11 12 13 х 
Рис.6.1
Пример 6.2
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах методом взвешенного скользящего среднего с шагом m=3 числа. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
| Год | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Число ПК | 4150,5 | 4558,3 | 5709,6 | 6684,0 | 7528,4 | 8267,3 | 8743,7 | 9288,1 |
Вычислим сглаженные значения числа ПК:
Вычислим цепной годовой прирост:
Вычислим спрогнозированные значения числа ПК для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
