ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 311
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример 1.4.4
Изменим постановку задачи примера 1.4.1, изменив ограничения (1) и (3).
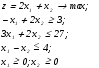
В этом случае произойдёт перемещение области допустимых решений как это показано на рис.4.4.
у
14
(2)
12
10 
8-
(3)
6 ОДР
4 
2 
1 2 3 4 5 6 7 8 9 х Целевая функция
Рис.4.4
Область допустимых решений (ОДР) ограничивается осью координат у1,
ограничением (1) и ограничением (2). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (0;1,5) а последняя – точкой максимума (6;4,5). В точке минимума z =3,в точке максимума z=16,5. Проверим выполнение всех ограничений в найденных точках.
Для точки минимума
0+2·1,5=3 выполняется как равенство;
3·0+2·1,5<27 выполняется;
0-1,5<4 выполняется.
Для точки максимума
-6+2·4,5=3 выполняется как равенство;
3·6+2·4,5=27 выполняется как равенство;
6-4,5<4 выполняется.
Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным.
Отметим, что решение четырёх примеров позволило найти минимумы и максимумы целевой функции в четырёх различных ОДР, определяемых задаваемыми ограничениями. В остальных областях координатного пространства могут быть найдены только точки минимумов целевой функции, то есть решение будет неполным, ввиду того что области для поиска точек максимума являются расходящимися.
Задание 1.5
Пример 1.5.1
Евклидово расстояние. Наиболее близкий сосед
Требуется разделить шесть объектов на два кластера. Объекты –
информационные системы характеризуются двумя признаками:
Х1-среднее время решения одной задачи в минутах;
Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы.
Значения признаков Х1 и Х2 для шести вариантов информационной системы представлены в таблице 5.1.1.
Таблица 5.1.1
| | 1 | 2 | 3 | 4 | 5 | 6 |
| X1 | 2 | 4 | 5 | 12 | 14 | 15 |
| X2 | 8 | 10 | 7 | 6 | 6 | 4 |
4>4>27>4>3>4>27>3>3>27>3>
По таблице 5.1.1 построен график, представленный на рис.5.1.1.
10 Х2
8
6 4 2
2 4 6 8 10 12 14 Х
1
Рис. 5.1.1
По формуле Евклида вычислены расстояния между объектами. Приведём два примера вычисления расстояний между 1 и 5 объектами и 2 и 6 объектами.
Процесс вычисления расстояния между 1 и 5 объектами поясняется на рис. 5.1.2; между 2 и 6 объектами на рис. 5.1.3.
10 Х2
8
6 4 2
