Файл: Тема Организационные подходы использования образовательных платформ для формирования представлений о геометрических понятиях в 5ом классе основной школы.doc

Одной из задач обучения является выработка у учащихся практических умений измерения и построения геометрических фигур с помощью чертежных и измерительных инструментов и без них(измерить –на глаз, начертить от руки и т.п.). Следует дать также первоначальное представление о точности построений и измерений .

Учитывая задачи, намеченные программой при изучении геометрического материала, следует широко использовать разнообразные наглядные пособия. Это демонстрационные, общеклассные модели геометрических фигур, требуются индивидуальные наглядные пособия.

Наиболее эффективными приемами изучения геометрического материала являются лабораторно-практические: моделирование фигур из бумаги, из палочек, проволоки; черчение, измерение и др.

При обучении в школе необходимо опираться на имеющийся опыт детей, уточнять и обогащать их представления.

У учащихся 1-4 классов надо формировать четкие образы точки, прямой и кривой линий, отрезка прямой. Задача учителя – научить вычленять, называть и правильно показывать эти фигуры, изображать их на бумаге и на доске, обозначать с помощью букв. Дети должны научиться измерять и чертить отрезки, заданной длинны .

Важнейшую роль при изучении геометрического материала в начальных классах играют геометрические задания, специально направленные на развитие у младших школьников пространственных представлений и воображения, их речи и мышления, на формирование практических умений и навыков. К ним можно отнести задания на:

А) классификацию геометрических фигур;

Б) деление фигур на части;

В) составление геометрических фигур заданной формы из других фигур;

Г) вычленение фигур на чертеже сложной конфигурации;

Д) распознавание фигур знакомых видов в окружающей обстановке;

Е) выяснение геометрической формы предметов или их частей.

В 1 классе учащиеся знакомятся с таким понятие как точка. Учитель при помощи следующих заданий: «Поставьте точку посередине клетки. Поставьте точку в верхнем левом углу клетки и т.д.» - учит ориентироваться в клетке. Затем эти знания можно применить на письме цифр.

После знакомства с прямой линией дети учатся ставить точки на прямой, проводить прямые через точки. Формирование представлений о прямой линии учащихся 1 класса происходит в процессе выполнения ими разнообразных упражнений. При этом, прямую сопоставляют с кривой линией. Дети должны научиться распознавать линию, начерченную в любом положении. При этом важно ее располагать не только горизонтально или вертикально, но и под различными углами.

---

В процессе выполнения упражнений, ребята знакомятся с некоторыми свойствами прямой. Например: при изображении линий, замечают, что через одну точку можно провести сколько угодно прямых или кривых линий. Или же то, что через две точки можно провести прямую линию, причем только одну, а кривых сколько угодно.

Также в ходе выполнения практических заданий учащиеся знакомятся с отрезком. Например, отметив на прямой две точки, учитель поясняет, что такую часть прямой называют отрезком. Позже делается сравнение отрезка с прямой, делается вывод, что прямая - не ограничена и какому-либо измерению поддается лишь часть прямой, ограниченная двумя, тремя точками – отрезок.

После изучения этих понятий формируются знания о таких фигурах, как многоугольник, угол, круг. При знакомстве с многоугольником вычленяются элементы фигуры: стороны, углы, вершины. Параллельно эти элементы рассматриваются на моделях .

Формирование понятия угла начинается с прямого угла, в процессе складывания листочков бумаги сначала вдвое, затем перегибая еще раз. Учитель предлагает развернуть сложенные листы. И ребята подмечают, что линии сгиба разделили лист на четыре угла, у которых одна вершина. Учащиеся делают вывод, что углы равны между собой, так как при складывании листа бумаги по линиям сгиба углы совпадают.

Понятие угла закрепляется в дальнейшем в процессе изучения многоугольников, например, при рассмотрении прямоугольника. В основе формирования представлений о прямоугольнике и квадрате, лежат определения: прямоугольник – это четырехугольник, у которого все углы прямые, а квадрат – это прямоугольник с равными сторонами.

Использование способствует постепенному осознанию детьми, что любой квадрат есть прямоугольник и в тоже время не всякий прямоугольник может быть квадратом .

С окружностью и кругом учащиеся начинают знакомиться в 3 классе. С помощью циркуля дети учатся чертить окружности, а также знакомятся с элементами окружности и круга – центром и радиусом. Именно в ходе практических упражнений усваиваются все эти сведения.

Часто приходиться сталкиваться с такой проблемой, что ребята путают окружность и круг. С целью предотвращения подобной ситуации, дают специальные упражнения, например: проведите окружность и раскрасьте круг, отметьте центр круга или окружности, а также точки, лежащие внутри круга, вне круга, на окружности.

С помощью уже знакомого понятия отрезка, учащиеся 1 класса знакомятся с понятием ломаной линии. Учитель предлагает по образцу построить линию из палочек или бумажных полосок. Тем самым дается название новой линии. Затем учащиеся чертят ломаные линии в своих тетрадях. При этом дети каждый раз подсчитываю, сколько отрезков и звеньев содержит построенная ломаная линия. Далее дается понятие незамкнутой и замкнутой линии, в процессе выполнения некоторых практических понятий .

---

Необходимо также установить связь между замкнутой линией и многоугольником, для которого ломаная линия является границей: замкнутая ломаная линия из трех звеньев ограничивает треугольник, а из четырех звеньев – четырехугольник и т.д.

Во 2 классе ребята знакомятся с измерением ломаных, то есть учатся находить длины ломаных линий. Учитель говорит, что для измерения ломаной необходимо измерить длины всех звеньев и сложить их. Для отработки навыка нахождения длины ломаной нужно включить достаточное количество упражнений на нахождение длины замкнутых и незамкнутых ломаных линий с разным количеством звеньев.

Позже, в 3 классе, на основе полученных знаний вводится понятие периметра многоугольника. Учитель поясняет, что периметром называется сумма длин всех сторон многоугольника.

Опыт показывает, что, не смотря на наличие в курсе математики 1-4 классов геометрического материала, большинство учащихся к концу обучения в 4 классе имеют лишь первые представления о рассматриваемых в начальных классах геометрических понятиях .

К тому же эти представления носят весьма фрагментарный характер. Учащиеся слабо владеют предусмотренной программой геометрической терминологией, далеко не всегда могут установить существенные признаки известных им геометрических фигур. Например, учащиеся начальных классов часто не различают прямую и отрезок, прямоугольник и квадрат и т.п. в связи с наличием в одной из двух данных фигур отдельных признаков, характерных для другой фигуры.

Такие же ошибки при изучении элементов геометрии нередко допускают и учащиеся 5 класса. Следовательно, при формировании геометрических понятий в 5-6 классах особое внимание должно быть направлено на выявление всех существенных признаков .

Таким образом, в начальной школе ведется накопление и развитие геометрических представлений у школьников, они знакомятся с понятиями «фигура», «плоскость», «прямая», с основными понятиями, связанными с окружность и кругом, с некоторыми терминами, овладевают элементарными навыками использования простейших инструментов. Это достигается систематическим проведением практических работ. Изготовление учащимися моделей геометрических фигур, вырезание, вычерчивание, получение фигур в результате перегибания листов бумаги, упражнения в распознавании фигур на чертежах и в реальной жизни, практические измерительные работы в классе и на местности играет основную роль на этой ступени обучения.

---

Самостоятельная задача формулировки определений перед учащимися не ставится. Однако они получают некоторые представления об определениях.

Таким образом, к 5 классу у учащихся накапливается значительный запас геометрических знаний и представлений, для дальнейшего обобщения и систематизации.

Геометрический материал в 5-6 классах распределен по всему курсу математики. Он составляет содержание так называемого пропедевтического или подготовительного курса геометрии. Основные цели этого курса – подготовить к сознательному усвоению систематического курса геометрии 7-9 классов, к изучению смежных дисциплин.

Пропедевтический курс геометрии связан с систематическим курсом планиметрии 7-9 классов как по содержанию, так и по идейной направленности.

Тем самым решается ряд задач:

1. 
   Знакомство в пропедевтическом курсе с основными геометрическими понятиями, с простейшими математическими фактами, являющимися аксиомами и теоремами, проведение первых логических обоснований, являющихся доказательствами, - все это служит подготовкой для раскрытия логического строения геометрии.
   
2. 
   Подготовительный курс геометрии знакомит учащихся с геометрической терминологией и символикой, которые используются и в систематическом курсе.
   
3. 
   Ознакомление с некоторыми видами отображения фигур готовит учащихся к сознательному усвоению идей геометрических преобразований.
   
4. 
   Знакомство с координатной прямой и координатной плоскостью создает основу для использования координатного метода при изучении отдельных разделов систематического курса геометрии.
   
5. 
   В 5 классе учащиеся имеют дело с такими геометрическими величинами, как длина, площадь, объем. Также знакомятся с величиной угла. В 6 классе вводятся формулы длины окружности и площади круга. В результате выполнения некоторых измерений и решения соответствующих задач на вычисления у учащихся складывается представление о величине как о неотрицательном числе. В процессе решения задач учащиеся знакомятся и со свойствами геометрических величин.
   
6. 
   В пропедевтическом курсе большое внимание уделяется в выработке у учащихся умений и навыков в выполнении построений с помощью основных геометрических инструментов, а также формированию у них рациональных приемов построения геометрических фигур. Эти умения будут необходимы как при изучении систематического курса геометрии, так и при изучении курса черчения.
   
7. 
   В подготовительном курсе геометрии реализуется идея связи теории с практикой. Теоретические положения раскрываются при решении задач жизненного характера.
   
8. 
   Пропедевтический курс включает задачи, позволяющие развивать у учащихся пространственные представления.
   
9. 
   Изучение материала пропедевтического курса геометрии подготавливает учащихся к усвоению некоторых смежных дисциплин, изучаемых в школе.
   

---

Содержание материала, изучаемого в 5 классе, составляют такие вопросы, как основные геометрические понятия: точка, прямая, плоскость, луч, отрезок, угол, треугольник; отношения – равенства фигур, измерение геометрических величин – длин отрезков, меры углов, площади прямоугольника, объема прямоугольного параллелепипеда. Эти вопросы не являются для учащихся 5 класса совершенно новыми, они рассматривались ими в начальной школе на интуитивном уровне. Учащимся известны понятия «окружность», «круг», «центр», «радиус», «диаметр». В систематическом курсе геометрии все эти понятия в дальнейшем получают свое развитие. В 5 классе ребята знакомятся со многими понятиями в оперативном плане, не определяя их, а лишь выделяя характерные свойства, существенные признаки в процессе решения задач.

В 5 классе учащиеся знакомятся также с простейшим символическим языком геометрии .

Курс геометрии 5 класса построен преимущественно на индуктивной основе.

1. 
   Учащиеся встречаются с такими понятиями, как «плоскость» и «прямая». Они должны научиться мысленно видеть, что прямая не имеет ни начала, ни конца, что она лежит в плоскости, что любая модель плоскости – это только часть плоскости. Следовательно, необходимо сформировать ясные представления об этих абстракциях у учащихся.
   

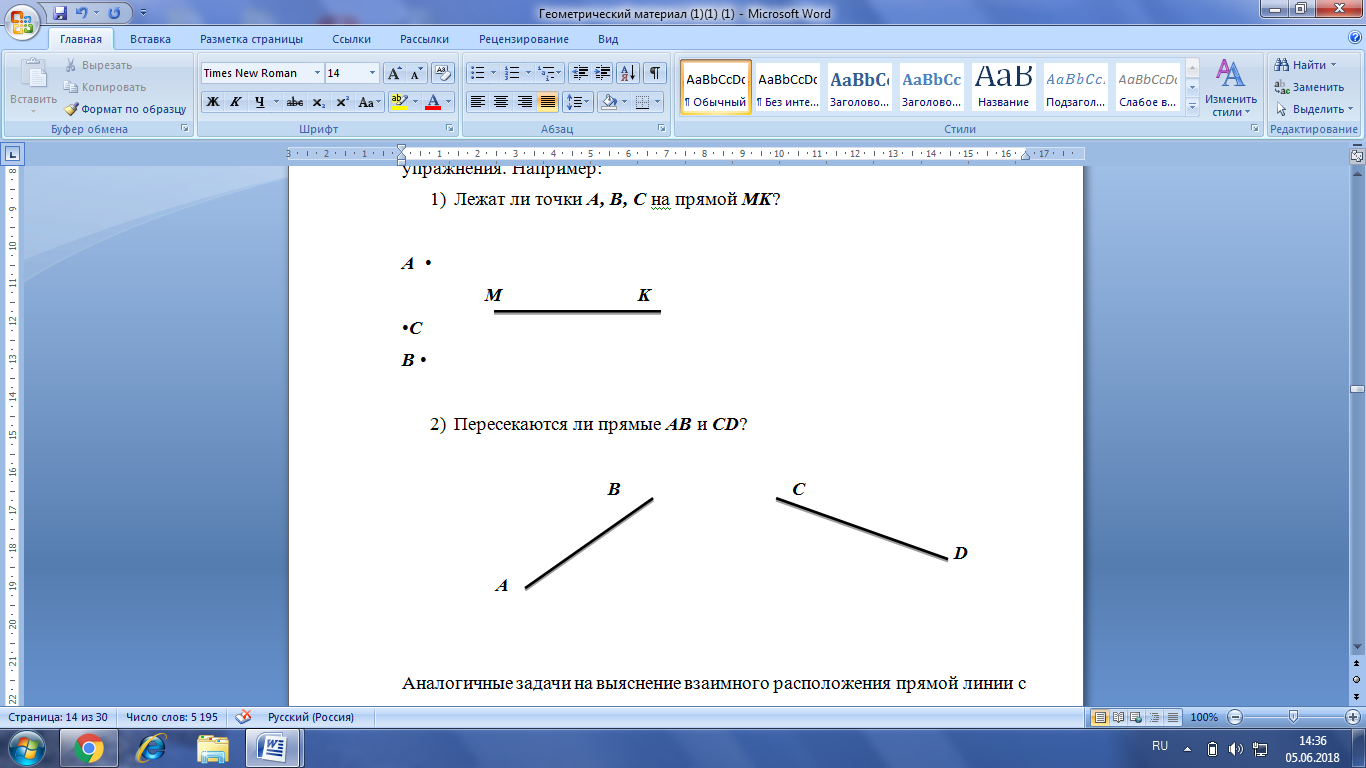
При изучении прямой линии важно создать представление о ее бесконечности. В этом помогут соответствующим образом подобранные упражнения. Например:

1. 
   Лежат ли точки A, B, Cна прямой MK?
   

---