Файл: Тема Организационные подходы использования образовательных платформ для формирования представлений о геометрических понятиях в 5ом классе основной школы.doc

Рис.1. Расположение прямой и точек

2. 
   Пересекаются ли прямые ABи CD?
   

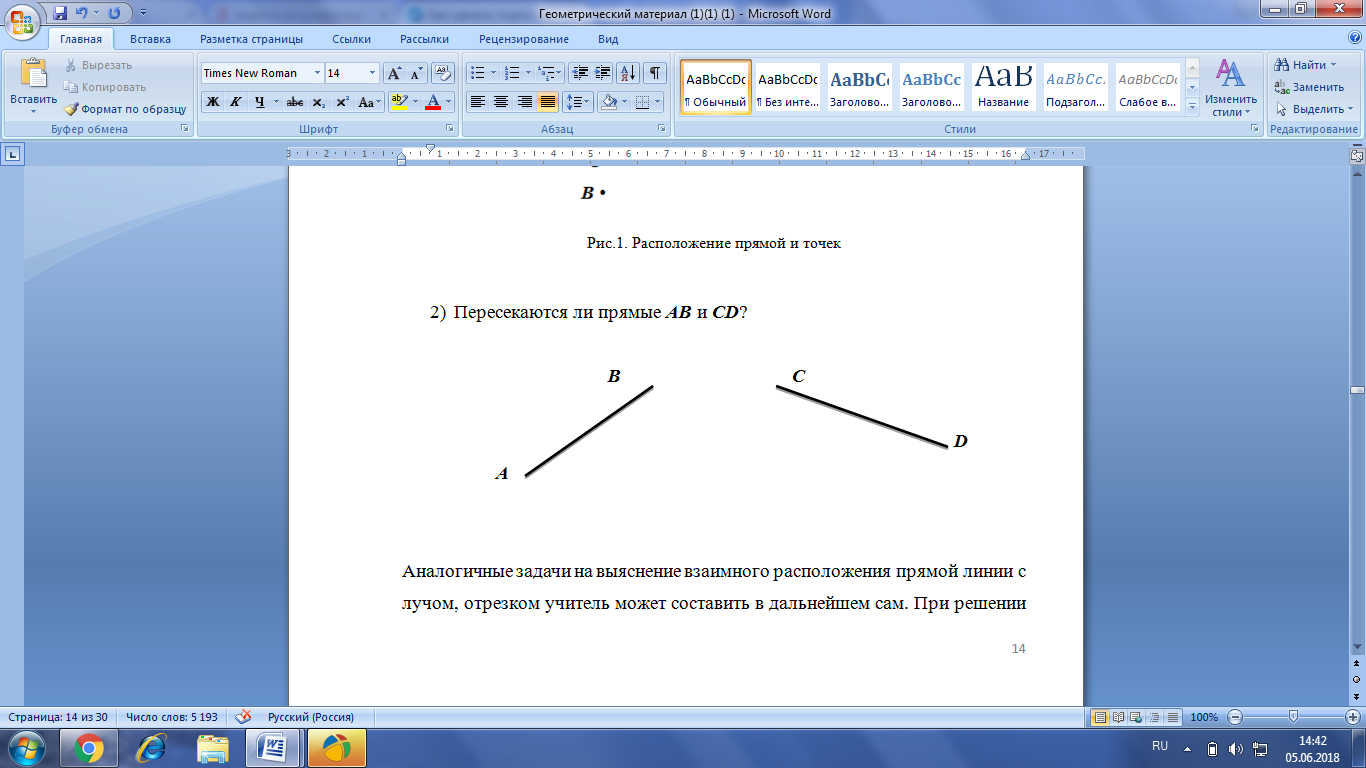
Рис.2. Пересекающиеся прямые
Аналогичные задачи на выяснение взаимного расположения прямой линии с лучом, отрезком учитель может составить в дальнейшем сам. При решении таких задач учащиеся представляют себе прямую линию безграничной, понимают, что на чертеже можно изобразить только часть прямой .

Далее учащиеся знакомятся с одним из основных свойств прямой линии:

- через любые две точки плоскости проходит единственная прямая;



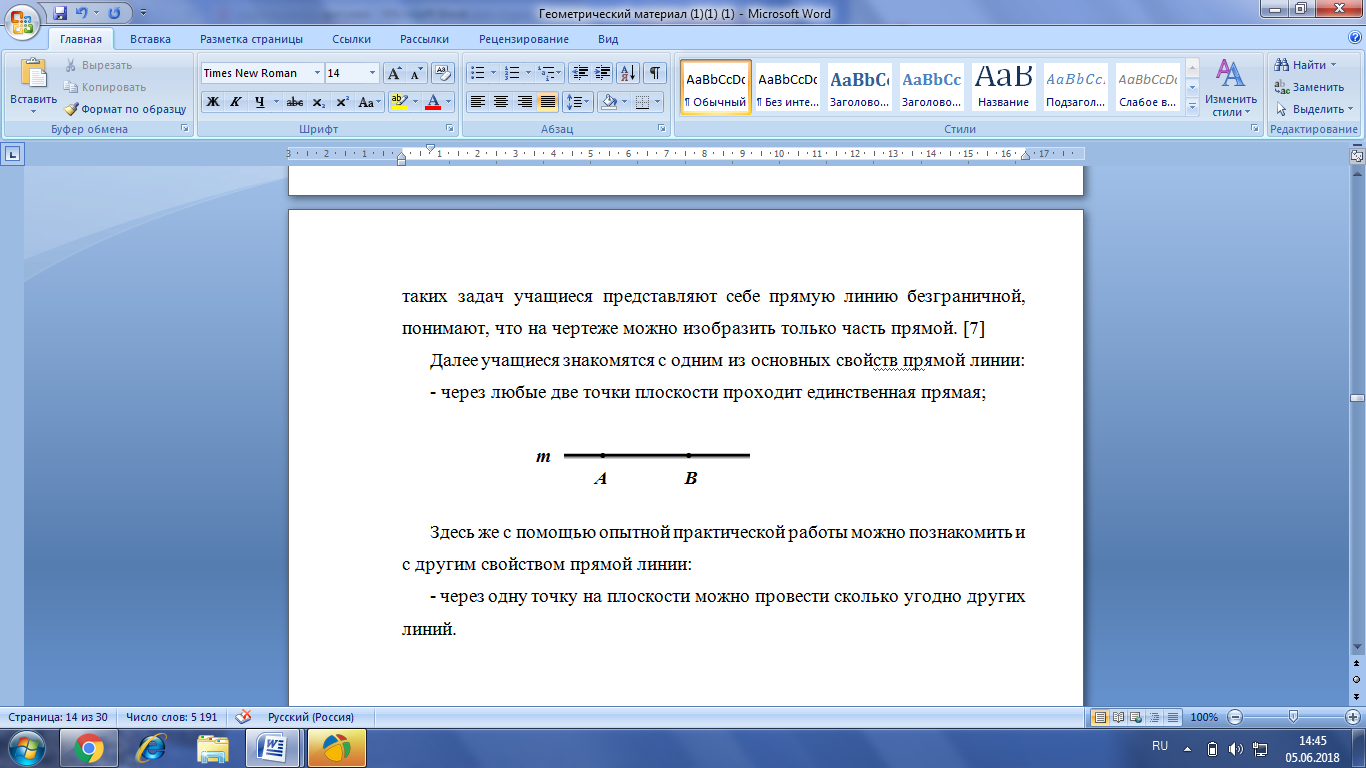
Рис. 3. Построение прямой через две точки
Здесь же с помощью опытной практической работы можно познакомить и с другим свойством прямой линии:

- через одну точку на плоскости можно провести сколько угодно других линий.



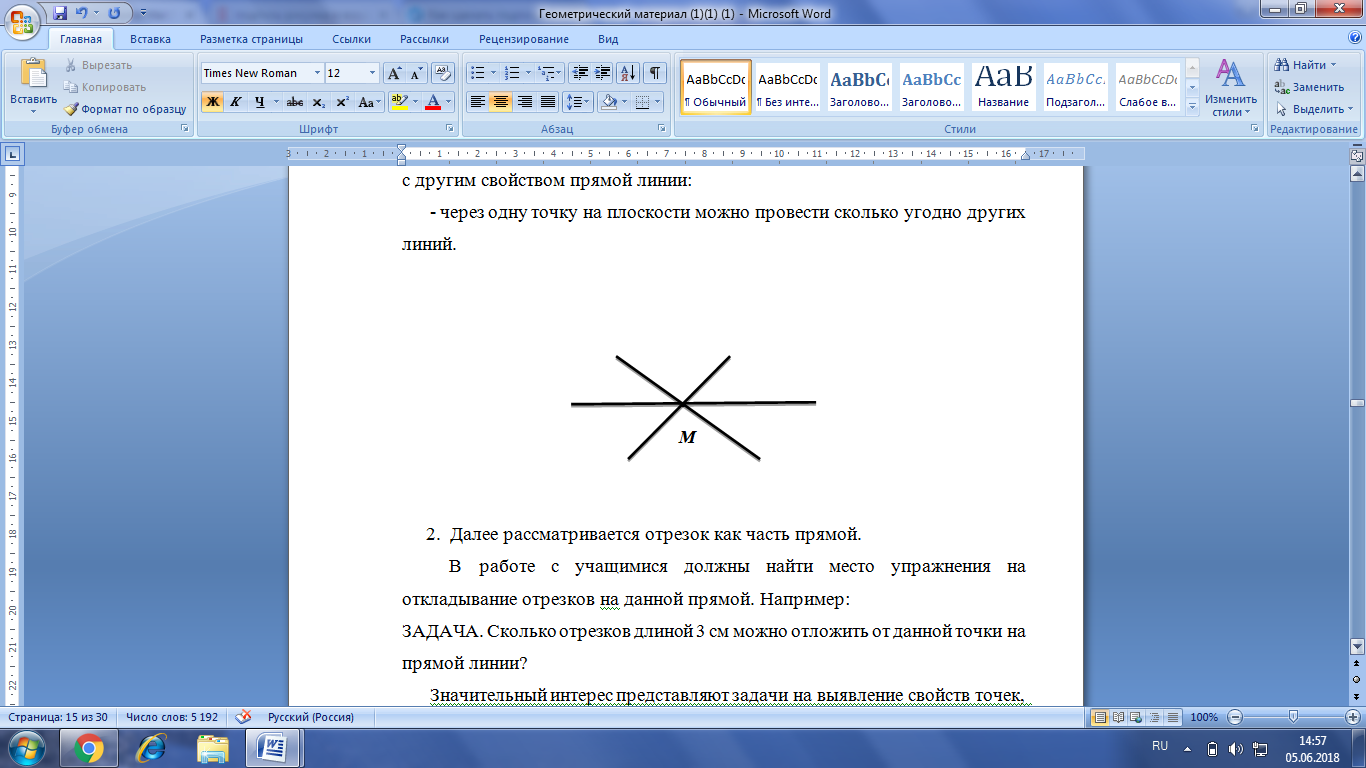
Рис. 4. Построение нескольких прямых через одну точку

2. 
   Далее рассматривается отрезок как часть прямой.
   

В работе с учащимися должны найти место упражнения на откладывание отрезков на данной прямой. Например:

ЗАДАЧА. Сколько отрезков длиной 3 см можно отложить от данной точки на прямой линии?

Значительный интерес представляют задачи на выявление свойств точек, принадлежащих и не принадлежащих ему, принадлежащих прямой и не принадлежащих ей. Например:

ЗАДАЧА. Отметьте в тетради точки Cи D. Проведите отрезок CD. Отметьте точку M, лежащую на отрезке CD. Лежит ли точка Mна прямой CD?

ЗАДАЧА. Сколько общих точек имеют:

а) отрезок ABи прямая CD;



Рис. 5.Отрезок и прямая, не имеющие общих точек
б) прямая MN и отрезок EK;



Рис. 6. Прямая и отрезок, имеющие общую точку

---

3. 
   При разъяснении понятия луча используется интуитивно ясное понятие «часть прямой». Особую трудность представляет формирование у учащихся представления о неограниченности луча. Для наглядности можно привести в качестве примера луч прожектора, направленный в ночное небо.
   

Особого внимания требует понятие лучей, дополнительных друг к другу. Здесь необходимо ввести упражнения для формирования понятий и обработки непривычной терминологии.

ЗАДАЧА. Назвать на прямой AC луч, дополнительный лучу OC.



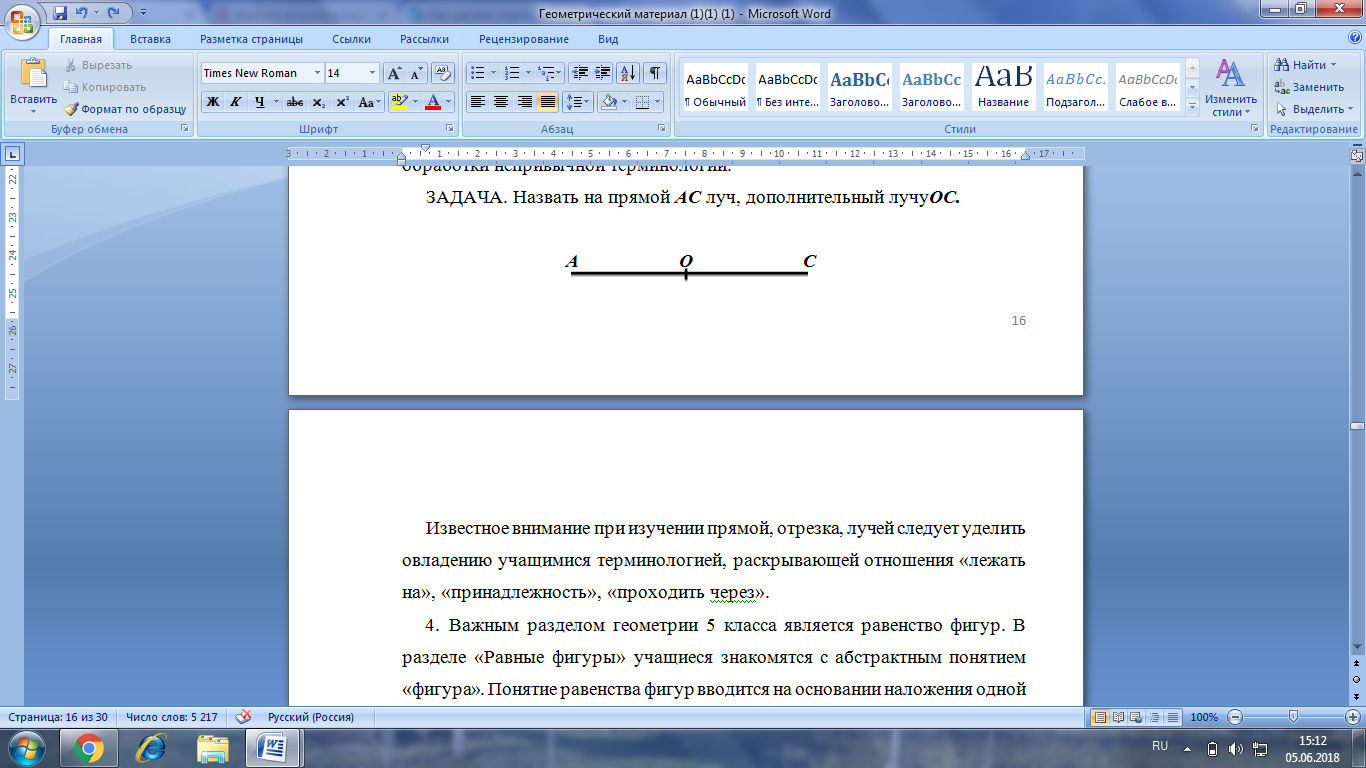
Рис. 7. Лучи, дополнительные друг к другу
Известное внимание при изучении прямой, отрезка, лучей следует уделить овладению учащимися терминологией, раскрывающей отношения «лежать на», «принадлежность», «проходить через».

4. 
   Важным разделом геометрии 5 класса является равенство фигур. В разделе «Равные фигуры» учащиеся знакомятся с абстрактным понятием «фигура». Понятие равенства фигур вводится на основании наложения одной фигуры на другую.
   

Две фигуры, которые можно наложить одну на другую так, чтобы они совпали, называют равными.

С помощью наглядных пособий учащиеся подводятся к выводу, что равные отрезки имеют равные длины, отрезки с равными длинами равны, а фигуры с равными площадями не всегда равны[10].

Вместе с тем учителю следует иметь в виду, что понятие «геометрическая фигура» играет важную роль при изучении геометрического материала в 5 классе. В изучаемом курсе это понятие является самым широким родовым, и к раскрытию его следует обратиться в самом начале изучения геометрического материала.

Формально-логического определения понятию «геометрическая фигура» не дается. Оно формируется на основе наблюдения учащимися окружающих тел. При этом необходимо опираться на интуитивно развитое умение ребят выделять одинаковые и не одинаковые формы у наблюдаемых вещей, на уже развитые у учащихся этого возраста способности не связывать понятие формы с материалом, из которого изготовлены изучаемые тела. Перед учащимися ставится задача: «Назовите известные вам геометрические фигуры». При ответе необходимо добиваться, чтобы учащиеся приводили примеры как пространственных, так и плоских фигур. При этом учащиеся должны называть не предметы, а собственно геометрические фигуры: треугольник, квадрат, куб, многоугольник, пирамиду, конус и т.д. На дом можно задавать задания практического характера: сделать модель одной из известных геометрических фигур (из пластилина, вырезать из бумаги и т.д.), в тетради сделать рисунок знакомых геометрических фигур, предметов, имеющих формы фигур. Аналогичные задания можно давать учащимся и при рассмотрении понятия «равные фигуры».

---

Далее рассматриваются высказывания: равные отрезки имеют равные длины; если длины отрезков равны, то отрезки равны; равные фигуры имеют одинаковую площадь.

При этом следует обратить внимание на обоснование этих высказываний, на их доказательность, подтверждение с помощью выполнения практических заданий.

Формированию таких умений могут способствовать следующие задания:

ЗАДАЧА. На рисунке 8 изображены пары фигур. Что общего и что различного в изображении этих фигур?



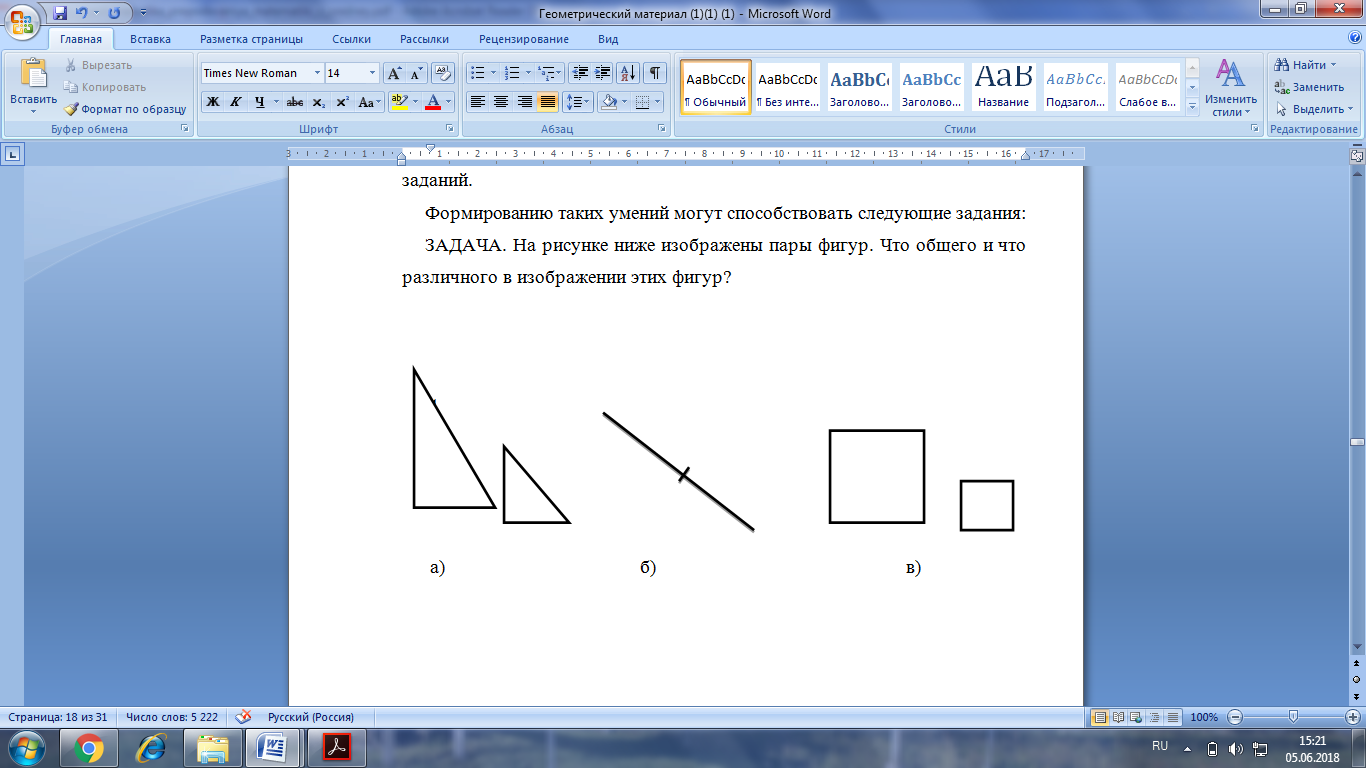
Рис. 8. Сходство и различие фигур.
ЗАДАЧА. Какие из отрезков AB, MP, CD, OK, MN,и BCравны, если AB=6 см, MP=5 см, CD=60 мм, OK=50мм, MN=6 см, BC=57 мм?

ЗАДАЧА. У четырехугольников ABCDи MNPQ все стороны имеют одинаковые длины. Равны ли эти четырехугольники?

При решении этой задачи следует предоставить возможность учащимся подумать и попытаться сделать самостоятельные выводы. Чертеж в данном случае служит средством подтверждения этих выводов.

Важное значение имеют упражнения на построение фигур, равных данным (на клетчатой бумаге), на узнавание равных фигур на чертеже.

Такие упражнения носят тренировочный характер, они помогают сформировать у учащихся умение выделить существенные принципы понятия геометрической фигуры, равенства фигуры, установить равенство фигур путем фактического наложения либо способом геометрического видения.

К понятию равенства необходимо обращаться при изучении любой из фигур в 5-6 классах.

5. 
   Многие геометрические сведения, с которыми знакомятся учащиеся до 5 класса, на определенном уровне обобщения рассредоточены по всем классам. Так, с понятием угла учащиеся знакомятся при изучении конкретных многоугольников – треугольников, четырехугольников и т.д. В 5 классе уже изучается луч. Здесь школьники учатся выделять вершины, стороны угла, усваивают, что два луча, выходящие из одной точки, определяют угол. Вводится значок обозначения угла « ». Сравнение углов осуществляется, так же как и сравнение других фигур, через наложение. Рассматриваются с учащимися различные виды углов: развернутый, прямой, острый, тупой. Понятие угла в 5 классе определяется как два луча, имеющие общее начало. ( Подход к определению угла генетический, так как вводится после построения самого угла ).
   

---

Н апример: Проведем на плоскости два луча ABи AC, имеющие общее начало в точке A. Получившуюся геометрическую фигуру называют углом.



Рис. 9. Построение угла

Важно обратить внимание учащихся на то, как правильно изображать и обозначать углы. При изучении этой темы учащимся следует предложить изготовить некоторые наглядные пособия. Эта работа сможет увлечь учащихся данной темой и закрепить определение угла и его элементов.

При изучении темы «Угол» нельзя не обратить внимание учащихся на разновидность углов (развернутый, прямой, острый, тупой). Учитель может предложить ученикам несколько задач, с помощью которых они закрепят эти понятия и научатся распознавать углы на глаз без применения инструментов (угольника, транспортира). Здесь интересна задача с часами (часы с движущимися стрелками также легко изготовить и использовать как наглядное пособие).

ЗАДАЧА. 1. Используя рисунок, записать все углы, которые равны углу AOB, углу AOD, углу AOL, углу BOD.

2.Для каких углов является биссектрисой луч OD?

3.Перечислить все острые, прямые, тупые и развернутые углы.

4.Какое время показывают часы, когда их стрелки образуют прямой угол и минутная стоит на 12?

Важная роль при обучении геометрии в 5-6 классах отводится решению задач. Предполагается, что изучение нового материала будет проходить главным образом в процессе решения задач, в процессе формирования умений и навыков применения знаний, а не в результате лишь заучивания теоретических положений.

Изучение геометрического материала опирается на творческое мышления учащихся. Поэтому задачи в учебнике занимают значительное место.

При рассмотрении вопроса измерения углов важное место имеют задачи вычислительного характера. Например:

ЗАДАЧА. Какую часть развернутого угла составляют углы в 30˚, 45˚, 60˚, 240˚? Какую часть прямого угла составляют углы в 30˚, 15˚, 60˚, 75˚?

Дидактические задачи носят различный характер. Некоторые из них решаются при изучении одного пункта учебника, другие предлагаются при изучении разных тем. Например, для формирования правильного представления о неограниченности прямой дидактические задачи предлагаются не только в пункте, посвященном изучению прямой непосредственно, но и при изучении углов и др.

---

.

Возможности образовательных платформ для преподавания математики в 5-ом классе основной школы

В концепции математического образования от 24.12.2013 года сказано, что качественное математическое образование поможет каждому занять достойное место в обществе, и я с этим согласна. Без базовой математической подготовки невозможна постановка образования современного человека. Формирование математического стиля мышления проявляется в определенных умственных навыках. Также изучение математики способствует эстетическому воспитанию человека.

Ученик может творить и рассчитывать на успех в любой области знаний тогда, когда он научиться в школе решать сложные задачи, анализировать, рассуждать, уметь доказывать утверждения. Математическая наука призвана формировать эти качества с раннего возраста, столь необходимые для успешной жизненной позиции каждого человека.

Сегодня в современном мире стремительно развиваются новые технологии, прогресс приходит во все сферы нашей жизни, в том числе и в образование. Надо понимать, для того, чтобы стать современным учителем, надо идти в ногу со временем, учить по-новому, используя инновационные компьютерные технологии в образовательном процессе.

Огромные перспективы и неограниченные возможности дает учителю в процессе обучения использование электронных образовательных платформ для творческой, мыслительной и исследовательской деятельности учащихся.

В своей работе почти на каждом уроке использую образовательные платформы, которых очень много в Интернете. Эти ресурсы позволяют учителю качественно подготовиться к уроку, рационально организовать и использовать учебное время. Красочное содержание позволяет заинтересовать обучающихся, сформировать у них предметные умения и универсальные учебные действия.

Показ на уроках презентаций, видеороликов, аудиоприложений сегодня это уже не новинка. На сегодняшний день основой образования являются цифровые технологии.

На помощь в этом учителям приходят компьютерные программы и интернет-ресурсы, которые стали особенно актуальными в условиях дистанционного обучения математике. Внедрение новых информационных технологий

---