ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 253
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2 Структурный анализ механизмов
3 Кинематический анализ механизма
3.1 Анализ зубчатого механизма
3.2 Построение плана положений
3.3 Анализ механизма методом диаграмм
3.4 Анализ механизма методом планов
4 Кинетостатический анализ механизма
Определение реакции во всех кинематических парах механизма
Силовой расчет ведущего звена механизма
Грохот разделяет любой кусковой или сыпучий материал на частицы разных размеров с помощью просеивающих поверхностей с калибровочными отверстиями. Сферы применения грохота – разделение на фракции горных пород, инертных строительных материалов, а также обезвоживание различных материалов (обогащенных углей, промытых руд).
Также грохотом называют машины для просеивания зерна злаковых и бобовых культур на механизированных токах, элеваторах, мельницах.
Обычно имеет высокую производительность, которая обеспечивается большой площадью поверхности грохочения (площадью сита), в отличие от вибрационных сит, которые обладают в общем случае малой и средней производительностью, могут быть предназначены для решения специфических задач (малая крупность деления – меньше 2 мм, обезвоживание и др.)
и имеют различные конструктивные исполнения.
Применение грохотов:
• Разделение на фракции угля, руд, щебня;
• Рассеивание материалов;
• Обезвоживание материалов (обогащенных углей, промытых руд).
Рабочие инструменты грохотов: короб грохота, рама, подвесные пружины, заточки приводного вала, подшипники, диски, дебалансы, вал, шкив.
Классификация грохотов:
По характеру движения рабочего органа или способу перемещения материала:
• Неподвижные грохоты (с неподвижной просеивающей поверхностью);
• Частично подвижные грохоты (с движением отдельных элементов просеивающей поверхности);
• Вращающиеся грохоты (с вращательным движением просеивающейся поверхности);
• Плоские подвижные грохоты (с колебательным движением всей просеивающей поверхности);
• Гидравлические грохоты (грохоты с перемещением материала в струе воды или пульпы).
По форме рабочей поверхности:
• Плоские грохоты (неподвижные грохоты, частично подвижные грохоты, плоские подвижные грохоты, гидравлические грохоты);
• Барабанные грохоты (вращающиеся грохоты);
• Дуговые грохоты (гидравлические грохоты).
По расположению просеивающей поверхности:
• Наклонные грохоты (в некоторых случая вертикальные);
• Горизонтальные грохоты (или слабонаклонные).
2 Структурный анализ механизмов

Рисунок 2 – Рычажный механизм
1. Механизм грохота, плоский механизм.
2. Обозначаем все звенья механизма, даем им названия:
1 - кривошип,
2 - ползун,
3 – кулиса,
4 - шатун,
5 – ползун,
6 - стойка, неподвижное звено.
3. Обозначаем все кинематические пары механизма, определяем их класс и вид:
О (6,1) - низшая, вращательная кинематическая пара 5 класса,
А (1,2) - низшая, вращательная кинематическая пара 5 класса,
А(2,3) – низшая, поступательная кинематическая пара 5 класса,
С (3,4) - низшая, вращательная кинематическая пара 5 класса,
D (4,5) - низшая, поступательная кинематическая пара 5 класса,
D (5,6) - низшая, поступательная кинематическая пара 5 класса,
4. Определяем степень подвижности механизма по формуле П.Л. Чебышева для плоских механизмов:
W = 3n – 2p5 – p4, (2.1)
где n – число подвижных звеньев;
p5 – число пар пятого класса;
р4 – число пар пятого класса.
N = 5; р5 = 7; р4 = 0;
W = 3·5 – 2·7 = 1.
Вывод: для данного механизма требуется одно входное звено.
5. Раскладываем механизм на структурные группы Ассура. Определяем их класс, вид и порядок:
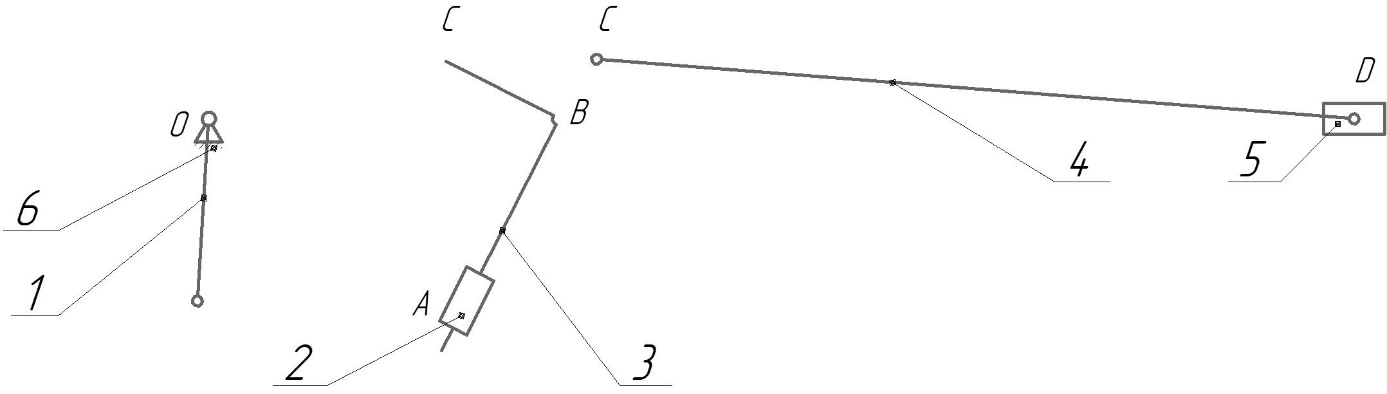
Рисунок 3 – группы Ассура.
6. Запишем формулу строения механизма
I (6, 1) → II2 (2, 3) → II2 (4, 5). (2.2)
7. Определяем класс механизма.
Механизм 2 класса, так как наивысший класс группы Ассура – второй.
3 Кинематический анализ механизма
3.1 Анализ зубчатого механизма
Согласно схемы передаточное отношение зубчатого привода, состоящего из последовательного соединения
планетарной передачи и рядовой передачи
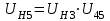 , (3.1)
, (3.1)где
 - передаточное отношение рядовой передачи.
- передаточное отношение рядовой передачи.
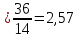
Согласно исходных данных зубчатый привод должен обеспечить передаточное отношение
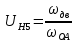 . (3.2)
. (3.2)Передаточное отношение планетарного редуктора задано по условию проекта
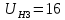 .
.Определим общее передаточное отношение зубчатого механизма.
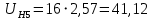 .
.Определим угловую скорость кривошипа ОА.
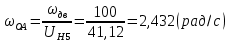 .
.3.2 Построение плана положений
Масштаб схемы. Приняв на чертеже (см. лист 1 приложения) отрезок ОА = 36 мм, находим:
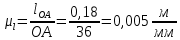 . (3.3)
. (3.3)В принятом масштабе пересчитываем отрезки на чертеже:
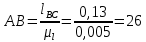 мм.
мм.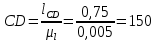 мм.
мм.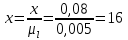 мм.
мм.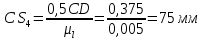
В принятом масштабе вычерчиваем схему механизма. Для построения 12 положений звеньев механизма разделим траекторию, описываемую точкой А кривошипа, на 12 равных частей. В качестве нулевого принимаем то положение кривошипа, при котором точка D ползуна занимает крайнее левое положение. Из отмеченных на окружности точек А0, А1…А11 проводим прямые через точку В, далее к этим прямым восстанавливаем перпендикуляры ВС=26 мм получаем точки С, из них раствором циркуля СD=150 мм получаем точки D на горизонтальной прямой.
3.3 Анализ механизма методом диаграмм
Расчет масштабного коэффициента для оси угла поворота входного звена:
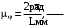 (3.4)
(3.4)где L - размер на чертеже (любое произвольно взятое число), мм (в нашем случае L = 120, мм).
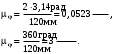
Масштаб по оси ординат графика перемещений:
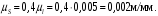
Масштаб по оси ординат графика аналога скоростей:
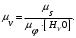 (3.5)
(3.5)Полюсное расстояние выбирается в следующих пределах [HV0] = 20…40 мм.
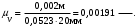
Для построения графика аналога скоростей принимаем [HV0] = 20 мм.
Масштаб по оси ординат графика аналога ускорений:
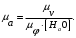 (3.6)
(3.6)Полюсное расстояние выбирается в следующих пределах
[Ha0] = 20…40 мм.

Для построения графика аналога скоростей принимаем [Ha0] = 20 мм.
Построение графиков.
На формате расчерчиваем три графика.
По оси «φ» откладываем выбранное при расчете масштабного коэффициента расстояние L = 120 мм. Это расстояние разбиваем на 12 равных участков (для 12 положений механизма). Для каждого положения механизма находим соответствующее перемещение ползуна.
Получившиеся точки соединяем ломаной кривой.
Построение второго графика.
На втором графике по оси «», в области отрицательных значений, откладываем выбранное при расчете масштабного коэффициента полюсное расстояние HVO20 мм.
С первого графика отрезок 01' переносим параллельно на второй график в точку HVи продолжаем до пересечения с осью V , получаем точку 1" .
На середине отрезка 0 1 (по оси ) ставим точку на высоте 01".
Аналогично поступаем на участке 12 . С первого графика отрезок 1'2' переносим параллельнона второй график в точку
HVи продолжаем до
пересечения с осью V , получаем точку 2". На середине отрезка 12 (по оси ) ставим точку на высоте 0 2". И т.д. Получившиеся точки соединяют плавной кривой.
Кривую на втором участке заменяют ломаной (соединяют точки пересечения графика с границами участков по оси «»). Третий график строят аналогично второму графику.
Расчет масштабных коэффициентов.
Масштаб по оси абсцисс:

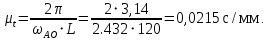
Масштаб по оси ординат графика скоростей:
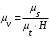
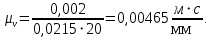
Масштаб по оси ординат графика ускорений:
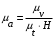
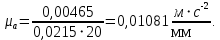
3.4 Анализ механизма методом планов
Определим линейную скорость т. А для ведущего звена.
Векторное уравнение движения точки А относительно центра вращения т. О:
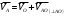 (3.7)
(3.7)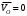 , т.к. эта точка неподвижна (находится в стойке),
, т.к. эта точка неподвижна (находится в стойке), (3.8)
(3.8)Скорость точки А будет направлена по касательной к окружности радиусом равным длине звена АО (перпендикулярно звену АО) в сторону вращения этого звена.
Определим ω1.
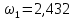 рад/с.
рад/с.Определяем скорость точки А.
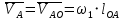 .
.
Масштаб планов скоростей вычисляем по формуле
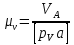 ,
,где VA – действительное значение скорости точки А,
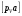 – отрезок, выражающий эту скорость на чертеже в мм.
– отрезок, выражающий эту скорость на чертеже в мм. 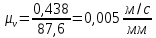
Записываем векторные системы уравнений для групп Ассура:
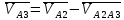
(3.9)
где
