ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 252
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2 Структурный анализ механизмов
3 Кинематический анализ механизма
3.1 Анализ зубчатого механизма
3.2 Построение плана положений
3.3 Анализ механизма методом диаграмм
3.4 Анализ механизма методом планов
4 Кинетостатический анализ механизма
Определение реакции во всех кинематических парах механизма
Силовой расчет ведущего звена механизма
— вектор скорости точки А во вращательном движении относительно точки О, направлена перпендикулярно оси звена ОА;
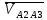 — вектор скорости точки А в поступательном движении относительно кулисы ВА, направлена по оси ВА;
— вектор скорости точки А в поступательном движении относительно кулисы ВА, направлена по оси ВА;
Скорости точек С и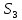 .
.
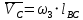
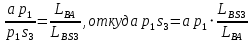
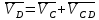 (3.10)
(3.10)
где — вектор скорости точки D в поступательном движении по горизонтали;
— вектор скорости точки D в поступательном движении по горизонтали;
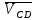 — вектор скорости точки D во вращательном движении относительно точки С, направлен перпендикулярно звену ВС;
— вектор скорости точки D во вращательном движении относительно точки С, направлен перпендикулярно звену ВС;
Строим планы скоростей. Построение начинаем от ведущего звена. Из точки рV, принятой за полюс плана скоростей, откладываем в направлении вращения кривошипа ОА перпендикулярно к нему вектор скорости точки А рVа = 87,6 мм. Из точки а проводим линию, параллельно оси звена ВА, а из полюса рV плана скоростей — линию, перпендикулярную оси ВА. Точка а3 пересечения этих линий даст конец вектора искомой скорости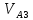 . Положение точки
. Положение точки 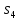 на плане скоростей определяем по соотношению
на плане скоростей определяем по соотношению
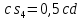 . (3.11)
. (3.11)
Действительные значения скорости каждой точки определяем по формулам:
 , (3.12)
, (3.12)
 , (3.12)
, (3.12)
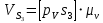 , (3.14)
, (3.14)
 . (3.15)
. (3.15)
 . (3.16)
. (3.16)
Получение значения сводим в табл. 3.1.
Определяем (табл. 3.2) угловую скорость кулисы ОА и коромысла СD для трех положений по формулам:
 . (3.17)
. (3.17)
 (3.18)
(3.18)
Таблица 3.1 - Значения скоростей точек рычажного механизма
Таблица 3.2 – Значения угловых скоростей, рад/с.
Определим полное ускорение т. А для ведущего звена.
Векторное уравнение движения точки А относительно центра вращения О:
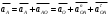 (3.19)
(3.19)
Нормальное ускорение направлено к центру вращения звена, от точки А к точке О, тангенциальное ускорение направлено перпендикулярно нормальному ускорению в сторону углового ускорения.
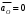 , т.к. эта точка неподвижна (находится в стойке).
, т.к. эта точка неподвижна (находится в стойке).
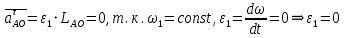 (3.20)
(3.20)
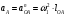
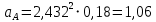 м/с2.
м/с2.
Ускорение точки А будет направлено параллельно звену АО от точки А к точке О (к центру вращения точки А).
Масштаб плана ускорений определяется по формуле

где aA - действительное значение ускорения точки А;
[pаa] = 106 мм — длина отрезка, изображающего на плане ускорений вектор нормального ускорения точки А кривошипа ОА.

Построение плана ускорений группы Ассура II класса 2-го вида (звенья 2 и 3) производим согласно векторному уравнению:
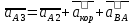
Или в развернутом виде
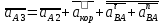 (3.21)
(3.21)
где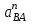 — нормальное ускорение точки А кулисы АВ при вращении ее вокруг точки В, направлено параллельно оси звена АВ от точки А к точке В;
— нормальное ускорение точки А кулисы АВ при вращении ее вокруг точки В, направлено параллельно оси звена АВ от точки А к точке В;
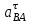
— тангенциальное ускорение точки кулисы ВА при вращении его вокруг точки В, направлено перпендикулярно к оси звена АВ;
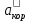 -кориолисово ускорение
-кориолисово ускорение
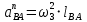
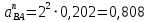 м/с2.
м/с2.
Его масштабная величина, обозначим ее через [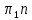 ] равна
] равна

 мм.
мм.
Кориолисово ускорение
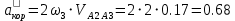 м/с2
м/с2
Его масштабная величина, обозначим ее через [а2р] равна
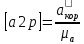
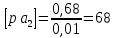 мм.
мм.
Из произвольной точки pa— полюса плана ускорений проводим вектор [pаa] параллельно звену ОА в 1 положении от точки A1 к точке О. На плане ускорений через точку а вектора [pаa] проводим прямую, перпендикулярную оси звена ВА, и откладываем на ней в направлении от точки отрезок [а2р] = 68 мм. Через конец этого вектора проводим прямую, перпендикулярную к оси звена ВА. Затем через полюс pa проводим прямую, параллельную оси звена ВА, и откладываем на ней в направлении от точки А к точке В отрезок [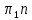 ] = 80,8 мм. И через конец этого отрезка проводим прямую параллельную ВА Точка пересечения этих прямых определит конец вектора [paа3].
] = 80,8 мм. И через конец этого отрезка проводим прямую параллельную ВА Точка пересечения этих прямых определит конец вектора [paа3].
Точку С, S3 и S4 на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков, аналогично как и для плана скоростей.
Численное значение ускорений точек звеньев найдем по формулам:


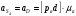
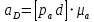
Определяем угловое ускорение ε2 звена АВ
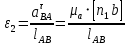
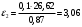 рад/с2.
рад/с2.
Для определения направления углового ускорения ε2 мысленно переносим вектор [n1b] с плана ускорений в точку В звена АВ. Считая точку А неподвижной, замечаем, что поворот звена будет против часовой стрелки.
Определяем угловое ускорение ε3 звена ВС
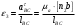
 рад/с2.
рад/с2.
Расчеты для остальных положений сведем в таблицы 3.3 и 3.4
Таблица 3.3 – Ускорения точек
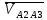 — вектор скорости точки А в поступательном движении относительно кулисы ВА, направлена по оси ВА;
— вектор скорости точки А в поступательном движении относительно кулисы ВА, направлена по оси ВА; Скорости точек С и
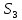 .
.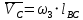
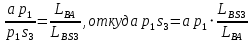
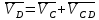 (3.10)
(3.10)где
 — вектор скорости точки D в поступательном движении по горизонтали;
— вектор скорости точки D в поступательном движении по горизонтали; 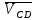 — вектор скорости точки D во вращательном движении относительно точки С, направлен перпендикулярно звену ВС;
— вектор скорости точки D во вращательном движении относительно точки С, направлен перпендикулярно звену ВС; Строим планы скоростей. Построение начинаем от ведущего звена. Из точки рV, принятой за полюс плана скоростей, откладываем в направлении вращения кривошипа ОА перпендикулярно к нему вектор скорости точки А рVа = 87,6 мм. Из точки а проводим линию, параллельно оси звена ВА, а из полюса рV плана скоростей — линию, перпендикулярную оси ВА. Точка а3 пересечения этих линий даст конец вектора искомой скорости
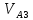 . Положение точки
. Положение точки 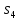 на плане скоростей определяем по соотношению
на плане скоростей определяем по соотношению 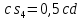 . (3.11)
. (3.11)Действительные значения скорости каждой точки определяем по формулам:
 , (3.12)
, (3.12) , (3.12)
, (3.12)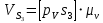 , (3.14)
, (3.14) . (3.15)
. (3.15) . (3.16)
. (3.16)Получение значения сводим в табл. 3.1.
Определяем (табл. 3.2) угловую скорость кулисы ОА и коромысла СD для трех положений по формулам:
 . (3.17)
. (3.17) (3.18)
(3.18)Таблица 3.1 - Значения скоростей точек рычажного механизма
| Длины векторов скоростей на плане скоростей, мм | | ||||
| Обозначение вектора | № положения | | |||
| 1 | 6 | 9 | | ||
| [pVa] | 87.6 | 87.6 | 87.6 | | |
| [pVc] | 51.88 | 47.58 | 94,8 | | |
| [a2a3] | 34.7 | 27.64 | 27,64 | | |
| [pVa3] | 80.43 | 83.33 | 83,13 | | |
| [pVs3] | 38.31 | 35.13 | 70 | | |
| [pVs4] | 31.7 | 39.39 | 78,85 | | |
| [pVd] | 19.87 | 37.67 | 75,57 | | |
| [cd] | 46.39 | 34.03 | 67,28 | | |
| Значения скоростей точек, м/с | |||||
| Обозначение скорости | № положения | | |||
| 1 | 6 | 9 | |||
| Va | 0.438 | 0.438 | 0.438 | | |
| Vc | 0,26 | 0.24 | 0,47 | | |
| Vа2а3 | 0,17 | 0.14 | 0,14 | | |
| VS3 | 0.19 | 0.18 | 0,35 | | |
| VS4 | 0.16 | 0.2 | 0,39 | | |
| Vd | 0.099 | 0.19 | 0,38 | | |
| Vcd | 0.23 | 0.17 | 0,34 | | |
Таблица 3.2 – Значения угловых скоростей, рад/с.
| Обозначение угловой скорости | № положения | ||
| 1 | 6 | 9 | |
| ????3 | 2 | 1.85 | 3,62 |
| ????4 | 0,31 | 0.23 | 0,45 |
Определим полное ускорение т. А для ведущего звена.
Векторное уравнение движения точки А относительно центра вращения О:
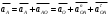 (3.19)
(3.19)Нормальное ускорение направлено к центру вращения звена, от точки А к точке О, тангенциальное ускорение направлено перпендикулярно нормальному ускорению в сторону углового ускорения.
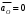 , т.к. эта точка неподвижна (находится в стойке).
, т.к. эта точка неподвижна (находится в стойке). 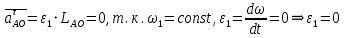 (3.20)
(3.20)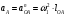
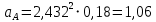 м/с2.
м/с2.Ускорение точки А будет направлено параллельно звену АО от точки А к точке О (к центру вращения точки А).
Масштаб плана ускорений определяется по формуле

где aA - действительное значение ускорения точки А;
[pаa] = 106 мм — длина отрезка, изображающего на плане ускорений вектор нормального ускорения точки А кривошипа ОА.

Построение плана ускорений группы Ассура II класса 2-го вида (звенья 2 и 3) производим согласно векторному уравнению:
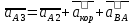
Или в развернутом виде
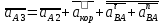 (3.21)
(3.21)где
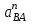 — нормальное ускорение точки А кулисы АВ при вращении ее вокруг точки В, направлено параллельно оси звена АВ от точки А к точке В;
— нормальное ускорение точки А кулисы АВ при вращении ее вокруг точки В, направлено параллельно оси звена АВ от точки А к точке В;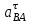
— тангенциальное ускорение точки кулисы ВА при вращении его вокруг точки В, направлено перпендикулярно к оси звена АВ;
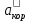 -кориолисово ускорение
-кориолисово ускорение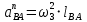
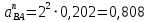 м/с2.
м/с2.Его масштабная величина, обозначим ее через [
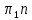 ] равна
] равна
 мм.
мм.Кориолисово ускорение
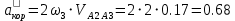 м/с2
м/с2Его масштабная величина, обозначим ее через [а2р] равна
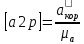
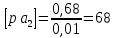 мм.
мм.Из произвольной точки pa— полюса плана ускорений проводим вектор [pаa] параллельно звену ОА в 1 положении от точки A1 к точке О. На плане ускорений через точку а вектора [pаa] проводим прямую, перпендикулярную оси звена ВА, и откладываем на ней в направлении от точки отрезок [а2р] = 68 мм. Через конец этого вектора проводим прямую, перпендикулярную к оси звена ВА. Затем через полюс pa проводим прямую, параллельную оси звена ВА, и откладываем на ней в направлении от точки А к точке В отрезок [
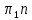 ] = 80,8 мм. И через конец этого отрезка проводим прямую параллельную ВА Точка пересечения этих прямых определит конец вектора [paа3].
] = 80,8 мм. И через конец этого отрезка проводим прямую параллельную ВА Точка пересечения этих прямых определит конец вектора [paа3].Точку С, S3 и S4 на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков, аналогично как и для плана скоростей.
Численное значение ускорений точек звеньев найдем по формулам:


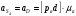
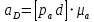
Определяем угловое ускорение ε2 звена АВ
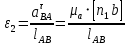
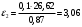 рад/с2.
рад/с2.Для определения направления углового ускорения ε2 мысленно переносим вектор [n1b] с плана ускорений в точку В звена АВ. Считая точку А неподвижной, замечаем, что поворот звена будет против часовой стрелки.
Определяем угловое ускорение ε3 звена ВС
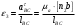
 рад/с2.
рад/с2.Расчеты для остальных положений сведем в таблицы 3.3 и 3.4
Таблица 3.3 – Ускорения точек
| Длины векторов ускорений, мм | |||
| Обозначение отрезка вектора ускорения | № Положения | ||
| 1 | 6 | 9 | |
| [πa] | 106 | 106 | 106 |
| [ра3] | 16,53 | 22,89 | 48.81 |
| [na3] | 26 | 18,36 | 67.92 |
| [πa3] | 84.88 | 79,8 | 164.11 |
| [πs3] | 40.43 | 33,74 | 138.2 |
| [πd] | 49.12 | 23,43 | 151.43 |
| [kd] | 39.26 | 38,59 | 68.77 |
| [cd] | 39.92 | 38,79 | 70.43 |
| [πc] | 54.75 | 45,7 | 187.14 |
| [πs4] | 48.03 | 30,7 | 166.54 |
| Значения ускорений, м/с2 | |||
| Обозначение ускорения | № Положения | ||
| 1 | 6 | 9 | |
| аa | 1.06 | 1.06 | 1.06 |
| аА2А3 | 0,1653 | 0,2289 | 0.4881 |
| аban | 0,808 | 0,777 | 1.49 |
| аbat | 0,26 | 0,1836 | 0.6792 |
| ac | 0,5475 | 0,457 | 0.7043 |
| аа3 | 0,4043 | 0,3374 | 1.382 |
| аs4 | 0,4803 | 0,307 | 1.665 |
| аd | 0.491 | 0.2343 | 1.514 |
| adct | 0.3926 | 0,3879 | 0.7043 |