ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 387
Скачиваний: 0
СОДЕРЖАНИЕ
Основные теоретические сведения
Краткая теория вопроса и метода.
Описание метода гидростатического взвешивания.
Краткая теория вопроса и метода измерения.
Краткая характеристика методов.
Описание экспериментальной установки.
Краткое знакомство и машиной Атвуда.
Описание прибора и теория метода.
Алгоритм обработки результатов многократных измерений.
При неизменном исходном положении грузов и одном и том же положении приемного столика будем иметь один и тот же путь. Тогда отношение ускорений согласно (4) обратно пропорционально отношению квадратов соответствующих промежутков времени движения.
Для двух различных
случаев согласно второму закону Ньютона
будем иметь
![]() ,
,![]() .
Здесь
.
Здесь![]() и
и![]() .
.
В этом случае
выполнение соотношения
![]() равносильно справедливости равенства
равносильно справедливости равенства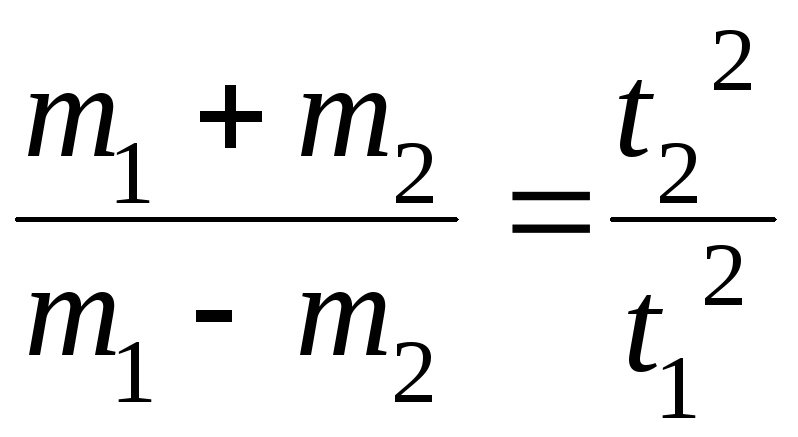 (6).
(6).
Заполните таблицу 4:
Таблица 4
|
m1 |
m2 |
m1+m2 |
m1-m2 |
t1 |
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сделать вывод на основе полученных вами числовых данных.
Вопросы к отчету.
Перечислить и дать определение всем кинематическим характеристикам движения материальной точки (путь, перемещение, скорость, мгновенная скорость, ускорение, линейное и угловое и т.д.).
Какие уравнения служат для описания движения?
Что называется динамическим уравнением движения?
Как можно определить момент инерции блока, пользуясь измерениями, в данной работе?
Относительно какой системы отсчета рассматривается движение грузов?
Сформулируйте законы Ньютона.
Выведите формулу (6) и покажите, как она подтверждает второй закон Ньютона.
Подсчитайте силу натяжения нити при равноускоренном и при равномерном движении грузов.
Выведите формулу для ускорения, учитывая силу трения.
Лабораторная работа № 2.2.
Изучение вращательного движения на крестообразном
маятнике Обербека.
Цель работы: изучить законы вращательного движения твердого тела и познакомиться с методом их экспериментальной проверки; определить моменты инерции крестовины и груза.
 Приборы
и принадлежности:
крестообразный маятник (прибор Обербека),
два груза разной массы (200 г и 300 г),
штангенциркуль, секундомер, масштабная
линейка, технические весы с разновесом.
Приборы
и принадлежности:
крестообразный маятник (прибор Обербека),
два груза разной массы (200 г и 300 г),
штангенциркуль, секундомер, масштабная
линейка, технические весы с разновесом.
Краткая теория вопроса.
Опр.1 Вращательное движение – движение, при котором все точки тела движутся по (коаксиальным) окружностям, центы которых лежат на одной и той же прямой, называемой осью вращения.
Для характеристики вращательного движения тела используются параметры, одинаковые для всех точек тела:
Угловое перемещение (угол поворота)
 – это угол между радиусами, проведенными
из центра окружности, описываемой
движущейся точкой, в начальный и
конечный моменты времени его движения.
Измеряется в радианах.
– это угол между радиусами, проведенными
из центра окружности, описываемой
движущейся точкой, в начальный и
конечный моменты времени его движения.
Измеряется в радианах.Угловая скорость
 – величина, показывающая изменение
угла поворота за единицу времени.
Измеряется в радианах в секунду.
Направление угловой скорости определяется
по правилу правого винта.
– величина, показывающая изменение
угла поворота за единицу времени.
Измеряется в радианах в секунду.
Направление угловой скорости определяется
по правилу правого винта.
Угловое ускорение
 – величина, показывающая изменение
угловой скорости за единицу времени.
Измеряется в радианах на секунду в
квадрате.
– величина, показывающая изменение
угловой скорости за единицу времени.
Измеряется в радианах на секунду в
квадрате.
При
описании вращательного движения
важнейшими динамическими
характеристиками являются момент силы
![]() и
момент импульса
и
момент импульса
![]() .
Момент силы характеризует
в динамике ее способность вызывать
вращение тел
и изменять угловую скорость. Различают
момент силы
относительно центра (точки) и относительно
оси.
.
Момент силы характеризует
в динамике ее способность вызывать
вращение тел
и изменять угловую скорость. Различают
момент силы
относительно центра (точки) и относительно
оси.
Опр.2
Моментом
силы
![]() относительно центра «О»называется
векторная
величина
относительно центра «О»называется
векторная
величина
![]() ,
где
,
где![]() —
радиус-вектор точки
приложения силы, проведенный из центра.
—
радиус-вектор точки
приложения силы, проведенный из центра.
Вектор
![]() направлен перпендикулярно плоскости,
в которой лежат векторы
направлен перпендикулярно плоскости,
в которой лежат векторы![]() и
и![]() .
.
Когда речь идет о моменте силы относительно оси, то в качестве точки О берется проекция точки приложения силы на эту ось!!! Направление вектора момента силы относительно оси определяется правилом буравчика.
М омент
импульса
омент
импульса![]() во
вращательном движении играет
ту же роль, что и импульс
во
вращательном движении играет
ту же роль, что и импульс
![]() в
поступательном движении.
в
поступательном движении.
Аналогично,
различают момент импульса относительно
оси
и относительно центра (точки). Момент
импульса относительно
центра «О» равен
![]() .
.
Опр.3
Скалярная величина, равная произведению
массы материальной точки
![]() на квадрат ее расстояния от оси вращения,
называетсямоментом
инерции материальной
точки относительно
оси вращения:
на квадрат ее расстояния от оси вращения,
называетсямоментом
инерции материальной
точки относительно
оси вращения:
I=mR2 (1).
Момент инерции
тела
(понимаемого как система материальных
точек или частиц)
относительно какой-либо оси равен сумме
моментов инерции всех материальных
точек тела относительно этой оси:
![]() .
.
Момент инерции
тела
(понимаемого как сплошная среда)
с плотностью
![]() вычисляется интегрированием по его
объему:
вычисляется интегрированием по его
объему:![]() ,
гдеdV-
элемент объема.
,
гдеdV-
элемент объема.
Момент инерции тела относительно какой-либо оси является физической величиной, характеризующей инертность тела по отношению к вращению вокруг этой оси.
Основной закон динамики вращательного движения твердого тела вытекает из уравнения моментов и имеет вид:
![]() (2), причем
(2), причем
![]() .
.
Здесь
![]() -
суммарный момент (относительно оси
вращения) всех
внешних сил, действующих на тело; I
- момент инерции тела относительно оси
вращения.
-
суммарный момент (относительно оси
вращения) всех
внешних сил, действующих на тело; I
- момент инерции тела относительно оси
вращения.
Если во время движения I=const, то уравнение (1) примет вид:
![]() (2’)
(2’)
Основной закон динамики вращательного движения устанавливает связь между угловым ускорением вращающегося тела, моментом приложенных к нему сил и его моментом инерции. Формулируется закон таким образом: угловое ускорение вращающегося тела пропорционально суммарному моменту всех сил, приложенных к нему, и обратно пропорционально моменту инерции этого тела.
Основной закон динамики вращательного движения – это второй закон Ньютона, записанный с использованием величин, характеризующих этот вид механического движения. Его значение – возможность записи уравнений движения любого вращающегося тела.
Описание метода и установки
Законы вращательного движения проверяются на установке, называемой маятником Обербека (рис. 2).
Маятник
Обербека представляет собой крестовину
(состоит из четырех стержней,
закрепленных наглухо крестом под углом
900друг к другу),
вращающуюся вокруг горизонтальной
оси. и
четырех грузов массой m,
которые могут перемещаться вдоль
стержней и закрепляться на различных
расстояниях (R)
от оси вращения. На
оси имеется двухступенчатый шкив
с радиусами r1
и r2,
на который наматывается нить. Выбор
радиуса шкива задаетс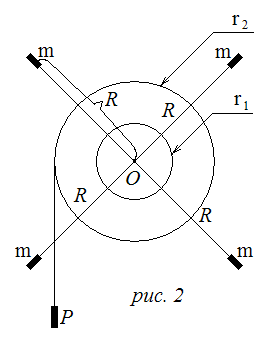 я
условиями эксперимента.Для
приведения прибора во вращательное
движение нить подвеса груза P
массой mгр.
наматывается на один из шкивов, и затем
груз поднимается на некоторую высоту
h
от поверхности табуретки или пола. Груз
отпускается и движется вниз с ускорением
a
вдоль вертикальной линейки, на которой
отмечаются начальное и конечное
положения при движении. С помощью
секундомера фиксируется точное время
движения подвеса. Зная
h
и время движения груза t,
можно вычислить ускорение:
я
условиями эксперимента.Для
приведения прибора во вращательное
движение нить подвеса груза P
массой mгр.
наматывается на один из шкивов, и затем
груз поднимается на некоторую высоту
h
от поверхности табуретки или пола. Груз
отпускается и движется вниз с ускорением
a
вдоль вертикальной линейки, на которой
отмечаются начальное и конечное
положения при движении. С помощью
секундомера фиксируется точное время
движения подвеса. Зная
h
и время движения груза t,
можно вычислить ускорение:
![]() (3).
(3).
При этом шкив со
стержнями и расположенными на них
грузами будет вращаться с угловым
ускорением
![]() ,
гдеr
- радиус шкива, с которого сматывается
нить, или, учитывая (3):
,
гдеr
- радиус шкива, с которого сматывается
нить, или, учитывая (3):
![]() (4).
(4).
Установим основные физические закономерности, наблюдаемые на маятнике Обербека.
При движении груза
P
на него действуют две силы, определяющие
его ускорение: сила тяжести
![]() и сила
натяжения шнура
и сила
натяжения шнура
![]() .
По второму закону Ньютона для грузаР
в проекции на направление движения:
.
По второму закону Ньютона для грузаР
в проекции на направление движения:
![]() откуда
откуда
![]() ,
,