Файл: ВсяМехЛАБраб2части.doc

Оценка погрешности производится в соответствии с видом измерения физической величины. Измерения бывают прямые и косвенные, однократные и многократные.

Правила, используемые при оценке погрешностей косвенных измерений:

• при сложении и вычитании абсолютные погрешности складываются;

• при умножении и делении относительные погрешности складываются;

• при возведении в степень и извлечении корня относительные погрешности умножаются на показатель степени;

• дисперсия суммы и разности величин равна сумме их дисперсий.

Причем, погрешность результата измерения всегда значительно меньше самого результата. Если это условие не выполнено, то к полученному результату нет никакого доверия и опыт нужно провести заново.

Средняя квадратичная погрешность функции z(a,b,…) многих переменных:

. Аналогично, для абсолютных погрешностей.

Алгоритм обработки результатов многократных измерений.

1. Найти среднее арифметическое значение х_ср измеряемой величины: .

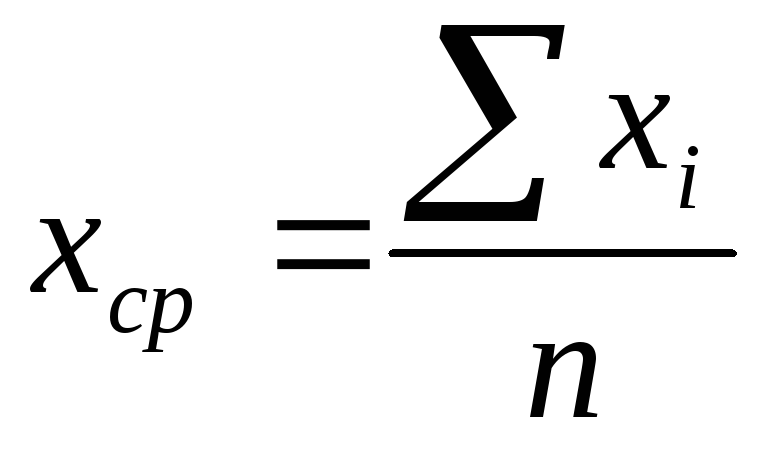2. Найти абсолютные погрешности отдельных измерений: .

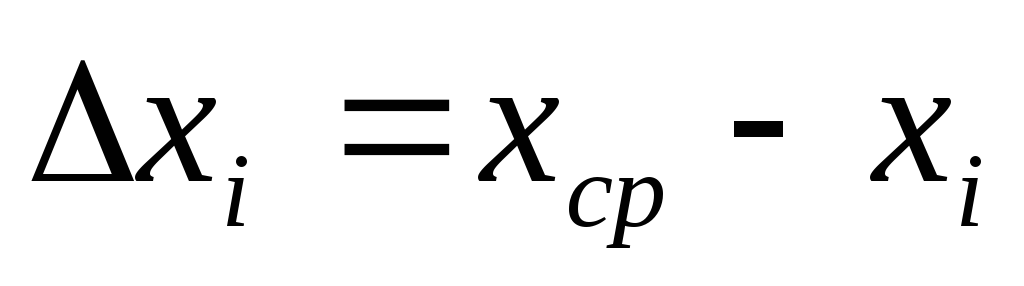3. Определяем среднюю квадратичную погрешность среднего значения: .

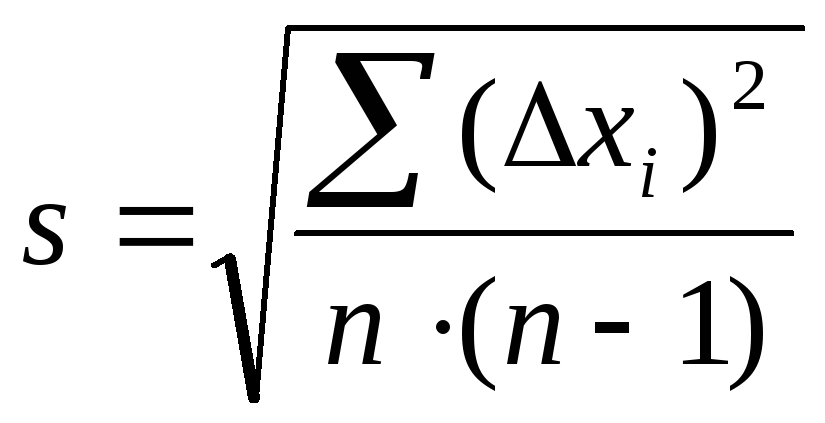4. По числу наблюдений n и выбранной вероятности Р по таблице определяем коэффициент Стьюдента t_s.

5. Вычисляем доверительный интервал для среднего значения измеряемой величины: Е=t_ss.

6. Записываем результат измерений в виде: Х=х_ср  Е (Р=Р_s).

7. Определяем относительную погрешность измерений в процентах: =.

В случае однократных прямых измерений с помощью измерительного прибора погрешность зависит от класса точности прибора К. К – число, равное предельно допустимой погрешности, выраженной в процентах от верхнего предела измерения прибора. Т.о. , гдес - цена деления прибора, N_m – наибольшее число делений в приборе. Погрешность от текущего измерения: х=0,01Кх, где х – показание прибора. Доверительная вероятность этих приборных измерений равна 1.

В случае многократных прямых измерений доверительная погрешность, соответствующая доверительной вероятности Р находится по формуле: .

Обработка результатов косвенных измерений:

1. выполнить прямые однократные или многократные измерения и найти средние значения аргументов; вычислить абсолютные погрешности каждого аргумента;

2. для аргументов определенных путем однократных измерений вычислить доверительные погрешности с заданной доверительной вероятностью х_i=Р_tx_пр;

3. для аргументов, найденных при многократных измерениях, определить средние квадратичные погрешности и по методу Стьюдента их абсолютные погрешности с нужной доверительной вероятностью;

4. найти абсолютную погрешность функции данных аргументов по формуле: .

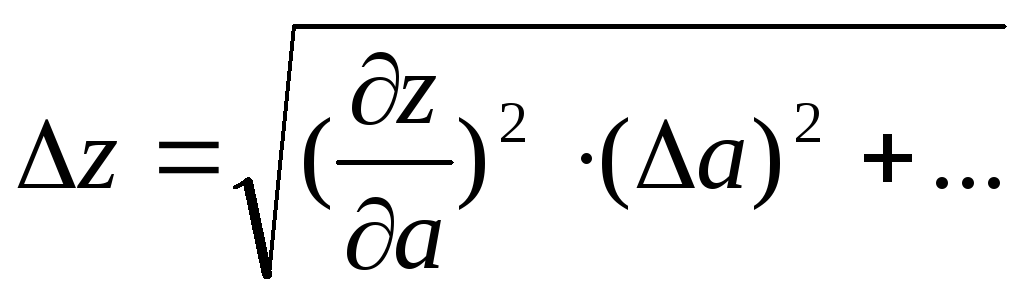5. среднее значение функции z: z_ср=z(a_ср, b_ср, …);

6. если функция удобна для логарифмирования, то т.к. 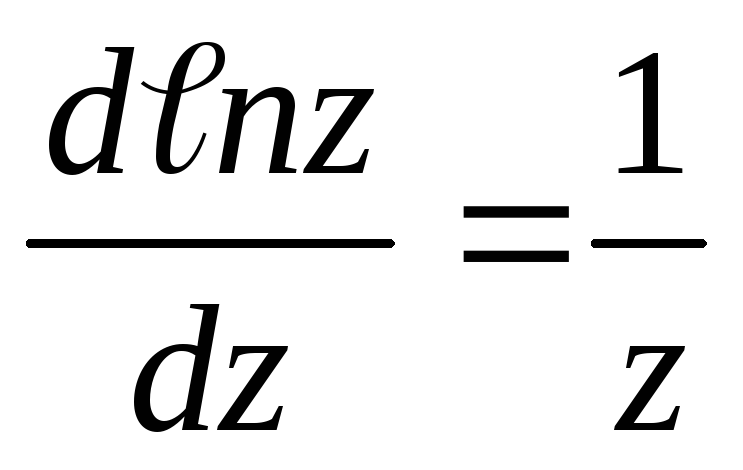, находим относительную погрешность:;

7. абсолютная погрешность находится как произведение относительной погрешности на значение самой величины;

8. окончательный результат записывается в виде: z = z_ср  z (P=P_z).

Приложение 2.

Типы погрешностей

Абсолютная и относительная погрешности

Опр.1 Абсолютная погрешность измерения физической величины определяется разностью , гдеx - измеренное значение физической величины, X - ее истинное значение, как правило, неизвестное.

Опр.2 Относительная погрешность измерения определяется отношением абсолютной погрешности к истинному значению измеряемой величины и выражается в процентах: .

На практике экспериментальной деятельности за Х принимается так называемое действительное значение измеряемой величины. В ходе учебного эксперимента будем за Х можно принимать: 1) среднее значение полученной величины (если измерения многократные); 2) известное табличное значение измеряемой величины; 3) результат однократного измерения (лишь для оценки относительной погрешности) при соответствующих расчетах абсолютной погрешности (например, по классу точности измерительного прибора).

Инструментальные и методические погрешности. Инструментальными (приборными) погрешностями средств измерений называются такие, которые принадлежат данному средству измерений, могут быть определены при его испытаниях и занесены в его паспорт. Например, погрешность весов из-за неравенства плеч или из-за того, что гири обладают тем или иным объемом  сила, с которой гиря давит на чашку весов, меньше ее истинного веса на вес вытесняемого ею воздуха (закон Архимеда). Инструментальные погрешности могут возникать вследствие несовершенства или неправильной технологии изготовления приборов. Методическая погрешность зависит от методики получения окончательного результата: 1) от пренебрежения по ходу вывода расчетной формулы тем или иным аргументом или условием протекания процесса и пр., 2) от наличия влияния на характер исследуемого процесса средств измерения и неучета этого влияния в расчетной формуле и т.д..

Систематические и случайные погрешности. Систематическими называют погрешности, которые при повторении наблюдений сохраняются постоянными или изменяются по определенному закону. Такие погрешности связаны, например, с ограниченной точностью изготовления приборов, их неправильной установкой, неверным выбором метода измерений, постоянным воздействием различных внешних факторов и т. д. Основной отличительный признак систематических погрешностей состоит в том, что они могут быть предсказаны и благодаря этому почти полностью устранены введением соответствующих поправок.

Случайные погрешности - непредсказуемые ни по знаку, ни по величине (либо недостаточно изученные) погрешности. Случайные погрешности обусловлены большим количеством трудно учитываемых факторов, влияющих как на измерительные устройства, так и на самого экспериментатора. Присутствие случайных погрешностей (в отличие от систематических) легко обнаруживается при повторных измерениях в виде некоторого разброса получаемых результатов. Таким образом, главной отличительной чертой случайных погрешностей является их непредсказуемость от одного отсчета к другому. Описание случайных погрешностей производится с помощью аппарата математической статистики и теории вероятностей.

Грубые погрешности. Грубые погрешности (промахи) определяются факторами чуждыми исследуемому процессу. Обычно они связаны с не тщательностью ведения измерений и записи результатов, а также сбоями в работе аппаратуры. Погрешности такого рода должны быть исключены путем проверок.

Погрешности отсчета. Отсчетом называют число, полученное при данном измерении по отсчетному устройству меры или прибора или полученное путем счета последовательных отметок или сигналов. Отсчет по шкале получают при помощи указателя, которым может быть стрелка (в амперметре), уровень жидкости (в мензурке), световой луч (в зеркальном гальванометре), конец измеряемого стержня (для линейки).

Если указатель установился точно на отметке шкалы, то за результат измерения принимается числовое значение этой отметки. Как правило же, указатель устанавливается между отметками шкалы, в этом случае можно оценить доли деления “на глаз”. Погрешность такого отсчета составляет 1-5 десятых доли деления, т.е. не превосходит половины цены деления шкалы. Как правило, независимо от того, к какой отметке ближе лежит указатель, его показание следует округлить до среднего арифметического двух значений, в промежутке между которыми он находится.

Рассмотренная погрешность отсчета, связанная с округлением показания средства измерения является случайной величиной и называется погрешностью округления.

Погрешность отсчета возникает не только от округления показаний прибора, но и по ряду других причин, например от параллакса. Параллакс заключается в видимом смещении указателя шкалы, вызываемом изменением точки наблюдения. Для уменьшения погрешности связанной с параллаксом линейки, например, изготовляют тонким или на краю линейки делают скос, кончики стрелки секундомера пригибают к шкале. В стрелочных приборах, для облегчения установки глаза, применяют зеркальную шкалу. Отсчет производят тогда, когда стрелка прибора закроет собой свое изображение в зеркале. Погрешность от параллакса может быть как случайной, так и систематической (например, если прибор постоянно находится сбоку от экспериментатора).