ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.04.2024
Просмотров: 92
Скачиваний: 0
2. Тригонометрический ряд
Полезно рассмотреть частный вид функциональных рядов, так называемые тригонометрические ряды. Членами тригонометрических рядов служат тригонометрические функции sin nx и
cos nx (n=1,2,3,…), взятые с числовыми коэффициентами. Тригонометрические функции, так же как и степенные, используются для разложения по ним функций.
О п р е д е л е н и е 1. Функциональный ряд вида
![]() +
+![]() (
(![]() cos
nx+
cos
nx+![]() sin
nx)
(1)
sin
nx)
(1)
где
![]() ,
,![]() и
и
![]() вещественные
числа, называется
тригонометрическим рядом.
вещественные
числа, называется
тригонометрическим рядом.
(Свободный член
обозначается
![]() для удобства некоторых дальнейших
выкладок).
для удобства некоторых дальнейших
выкладок).
Каждый член
тригонометрического ряда является
периодической функцией с периодом 2![]() .
Действительно, постоянную
.
Действительно, постоянную![]() можно, как известно, считать периодической
функцией с каким угодно периодом, в
частности с периодом2
можно, как известно, считать периодической
функцией с каким угодно периодом, в
частности с периодом2![]() ;sin
x
и cos
x
(п=1)
имеют период 2
;sin
x
и cos
x
(п=1)
имеют период 2![]() ;sin
2x
и cos
2x
(п=2),
как известно, имеют период
;sin
2x
и cos
2x
(п=2),
как известно, имеют период
![]() ,
следовательно, число2
,
следовательно, число2![]() также является их периодом; вообщеsin
пx
и cos
пx
имеют период, равный
также является их периодом; вообщеsin
пx
и cos
пx
имеют период, равный
![]() ,
и, следовательно, число
,
и, следовательно, число![]() также является их периодом. Поэтому
можно сказать, что если ряд (1) сходится,
то его сумма является периодической
функцией с периодом2
также является их периодом. Поэтому
можно сказать, что если ряд (1) сходится,
то его сумма является периодической
функцией с периодом2![]() .
.
Изучим одно свойство системы тригонометрических функций.
О п р е д е л е н и
е 2. Система
функций
![]() (х),
(х),
![]() (х),…,
заданных
в некотором
промежутке
(х),…,
заданных
в некотором
промежутке
![]() ,
называется
ортогональной системой в
,
называется
ортогональной системой в
![]() ,если
,если
![]() при n
при n![]() m
(2)
m
(2)
и
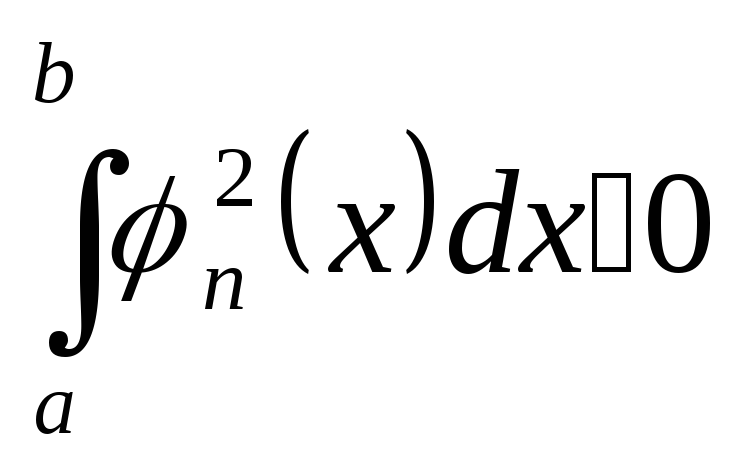 при любом
п.
при любом
п.
(Последнее неравенство означает, в частности, что ни одна из функций системы не есть тождественный нуль.)
Т е о р е м а. Система функций
1, cos x, sin x, cos 2x, sin 2x,…, cos nx, sin nx,… (3)
является
ортогональной системой в промежутке
![]() .
.
Доказательство. Проверим выполнение равенства (2) для функций системы (3). Для этого надо проверить непосредственным вычислением равенство нулю интегралов от произведений различных функций системы (3), то есть от произведения двух косинусов с разными аргументами, двух синусов с разными аргументами, произведения косинуса на синус (с любыми аргументами) и произведения любого синуса или любого косинуса из системы (3) на единицу, которая является первой функцией системы (3).
Итак, проводим указанные выкладки:
а)
![]()
б)
![]()
в) Пусть n![]() m:
m:
![]()
в силу пункта а), так как (m+n) и (m-n) – целые числа, отличные от нуля.
г) Пусть n![]() m:
m:
![]()
опять в силу пункта а).
д)
![]()
в силу пункта б)
первый интеграл равен нулю; второй
интеграл равен нулю в силу пункта б) при
n![]() m;
если же n=m,
то этот интеграл равен нулю потому, что
подынтегральная функция тождественно
равна нулю: sin(m-n)x=sin0=0.
m;
если же n=m,
то этот интеграл равен нулю потому, что
подынтегральная функция тождественно
равна нулю: sin(m-n)x=sin0=0.
Также проверяется легко и второе требование:
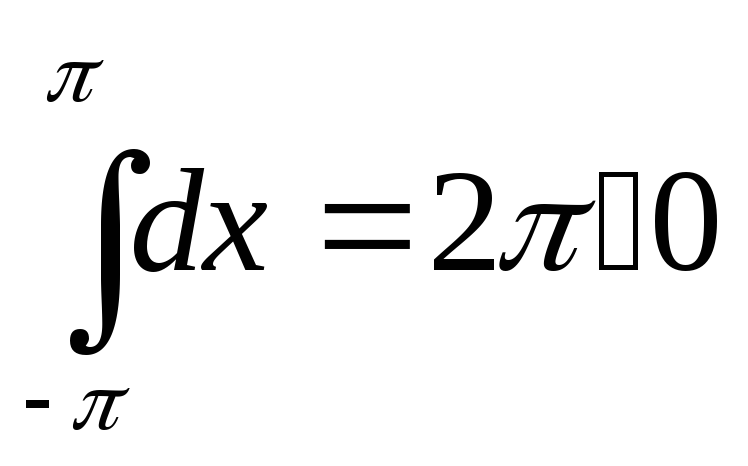
![]()
![]()
Таким образом, теорема доказана.
Примеры
№1Является ли система функций
![]()
![]()
ортогональной?
1.
![]()
2.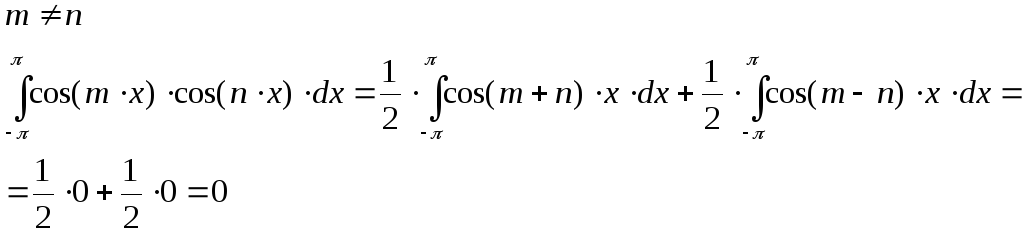
3.![]()
![]()
Таким образом система является ортогональной.
![]()
№2Является ли система функций
![]()
ортогональной.
1.![]()
2.![]()
3.![]()
![]()
Таким образом, система является ортогональной.
№3
![]()
![]()
![]()
![]()
Функция является ортогональной.
3. Ряд фурье
Ранее было введено понятие ряда Тейлора. Так был назван специальный ряд, коэффициенты которого вычислялись по определенному правилу с помощью некоторой заданной функции f(х). Таким образом, каждой бесконечно дифференцируемой функции ставился в соответствие ее ряд Тейлора.
Изучая
тригонометрические ряды, можно пойти
по такому же пути. Возьмем некоторую
функцию f(х),
определенную в
![]() (а может быть, и в большем промежутке
или даже на всей числовой оси), и составим
с ее помощью следующие числа:
(а может быть, и в большем промежутке
или даже на всей числовой оси), и составим
с ее помощью следующие числа:
![]() ,
,
![]() ,
,![]() (1)
(1)
О п р е д е л е н и е. Тригонометрический ряд, коэффициентами которого служат числа (1), называется рядом Фурье функции f(х), а сами числа (1) называются коэффициентами Фурье функции f(х).
Для того чтобы
можно было вычислить коэффициенты
Фурье, нужно, очевидно, предположить,
что функция f(х)
интегрируема в
![]() .
.
Итак, каждой функции
f(х),
интегрируемой в
![]() ,
можно поставить в соответствие ее ряд
Фурье:
,
можно поставить в соответствие ее ряд
Фурье:
f(х)~![]() (2)
(2)
Докажем предварительно следующее утверждение, относящееся к любому функциональному ряду.
Л е м м а. Если
функциональный ряд
![]() сходится равномерно в
сходится равномерно в![]() и
и![]() – некоторая ограниченная в
– некоторая ограниченная в![]() функция, то ряд
функция, то ряд![]() также равномерно сходится в
также равномерно сходится в![]() .
.
Доказательство.
Тот факт, что данный ряд
![]() равномерно
сходится в
равномерно
сходится в
![]() означает
следующее: для всякого ε>0
найдется номер N
такой, что неравенство
означает
следующее: для всякого ε>0
найдется номер N
такой, что неравенство
![]() <ε
справедливо для всякого n
<ε
справедливо для всякого n
![]() N
и для любого
N
и для любого
![]()