Файл: Матан(3блок).doc

,

Т.к. корни разные то

Найдем матрицу S:

Т.к. (справа). Пусть, тогда

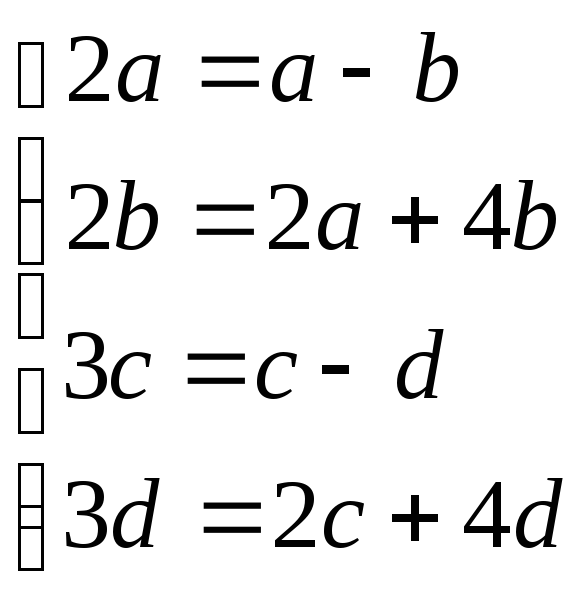
при

Следовательно,

Интегрируя уравнение , где. Согласно формуле

получаем

Найдем по формуле

Ответ: .

19. Построить функцию Грина для следующей краевой задачи

А)

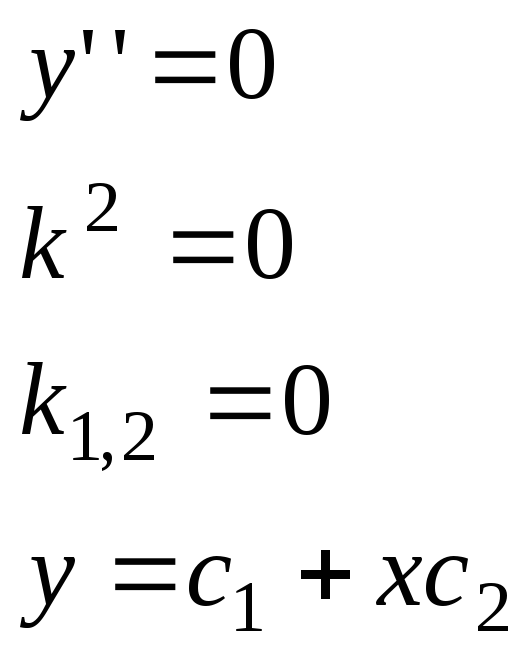
Условию удовлетворяет нормаль

удовлетворяет

Ф-цию Гр ищем в виде

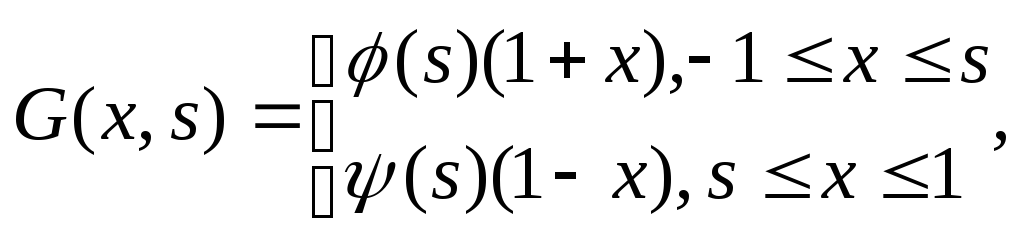
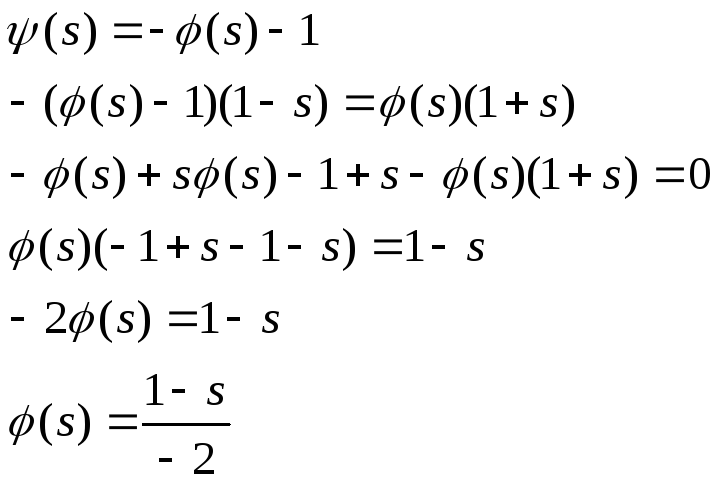
Ответ

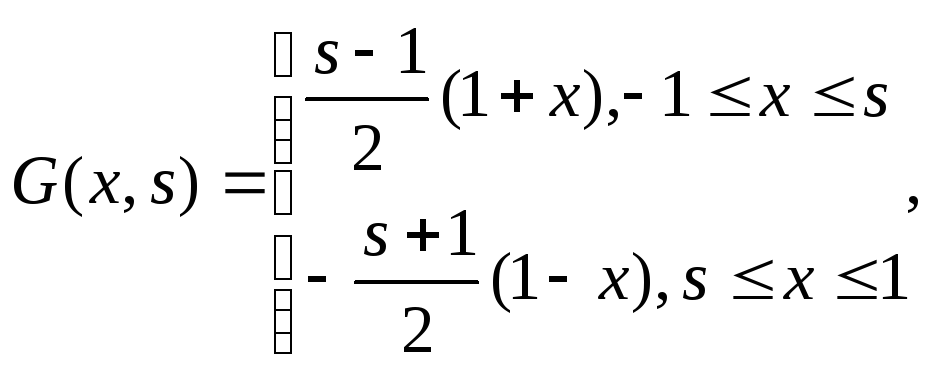
19. Построить функцию Грина для следующей краевой задачи

Б)

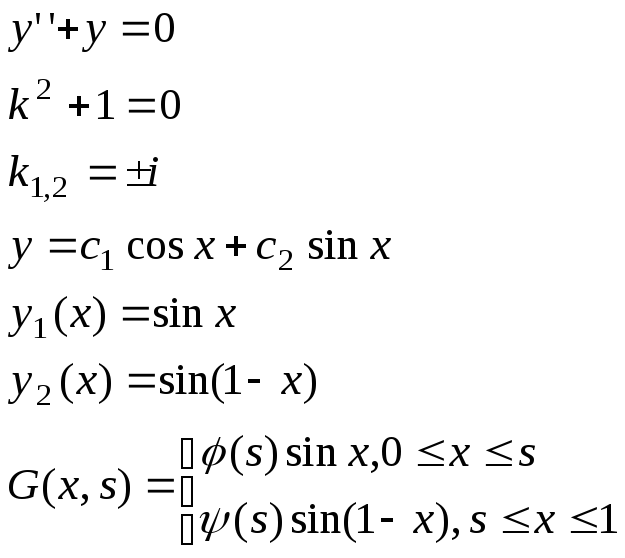
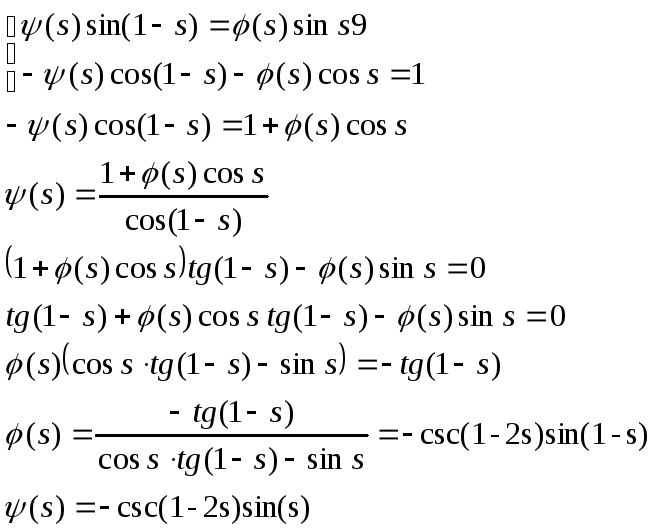
Ответ:

20. Привести к каноническому виду уравнение.

А)

1)

- гипер-ий тип

2) найдем уравнение характеристик

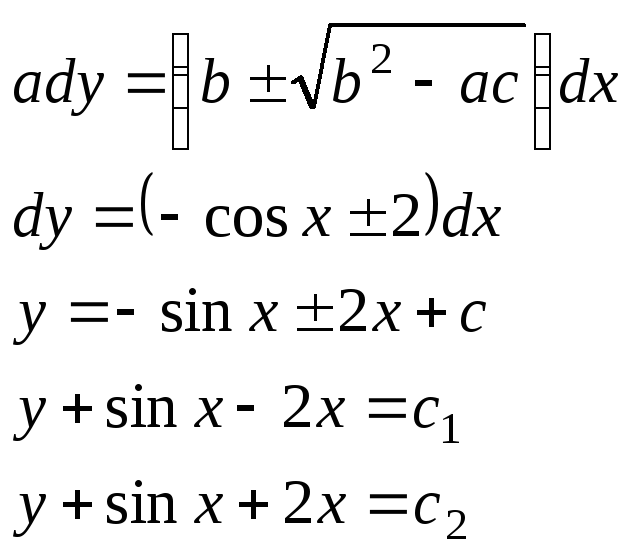
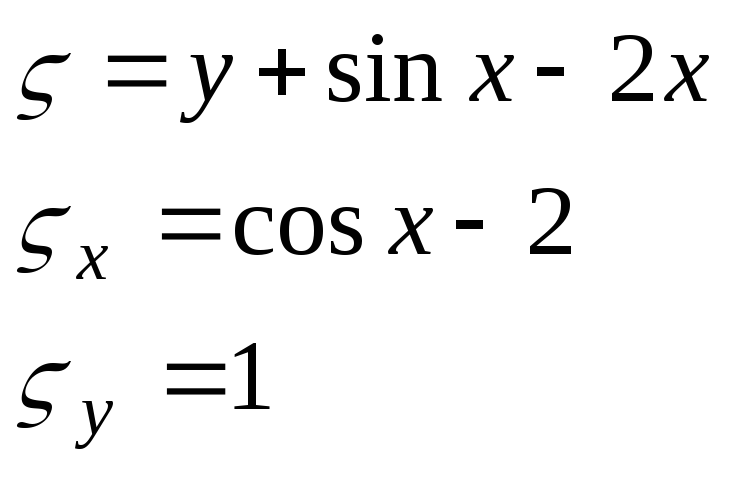
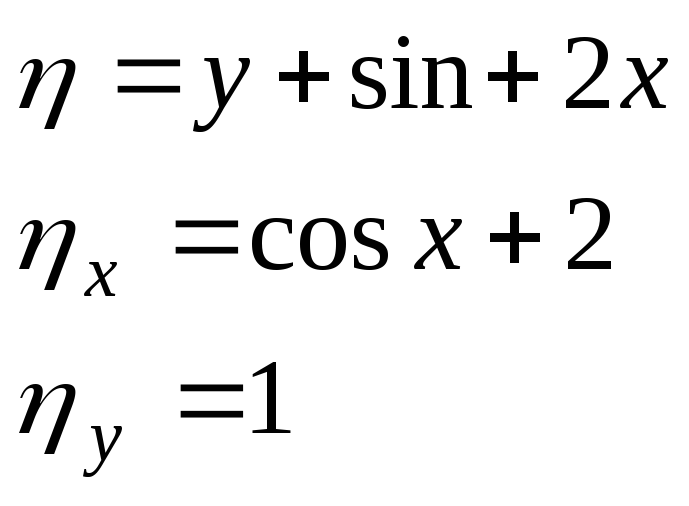
3)

4)

=> =>

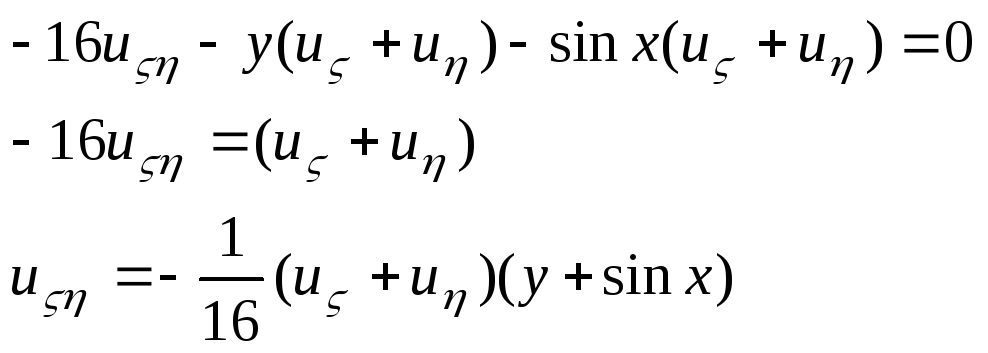
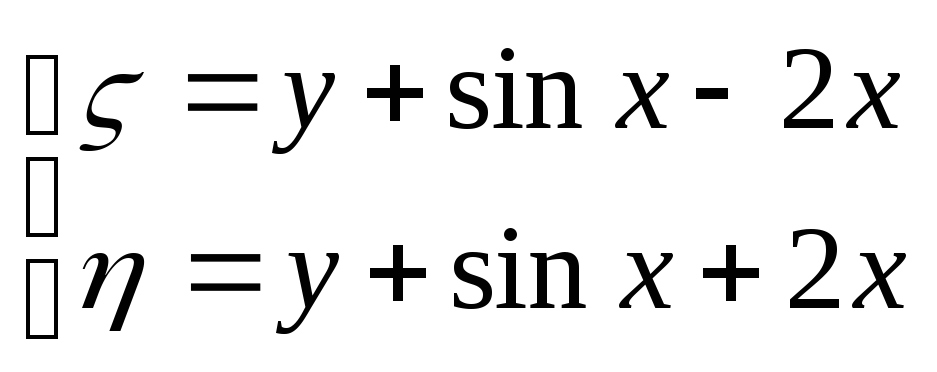Тогда

20. Привести к каноническому виду уравнение

Б)

1)

(т.к. по усл.)- эллиптич. Тип

2) найдём уравнение характеристик

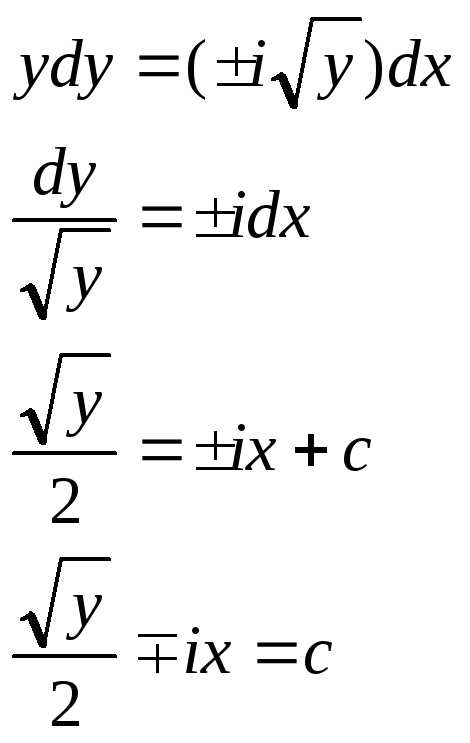
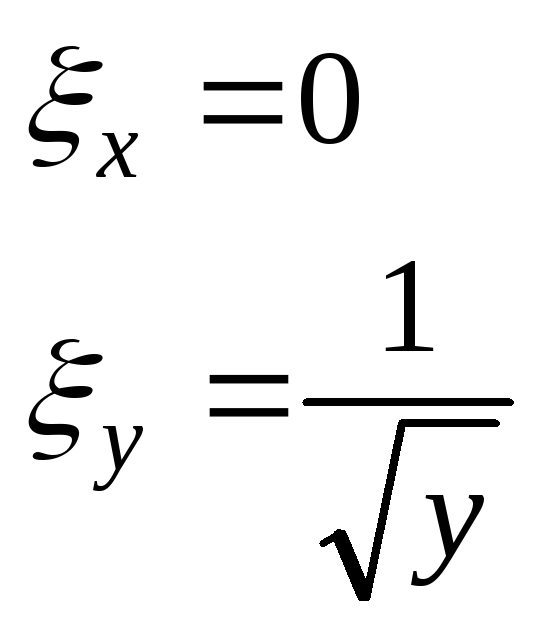
3)

Ответ:

20. Привести к каноническому виду уравнение

В) .

1)

- эллиптич. тип

2) найдём уравнение характеристик

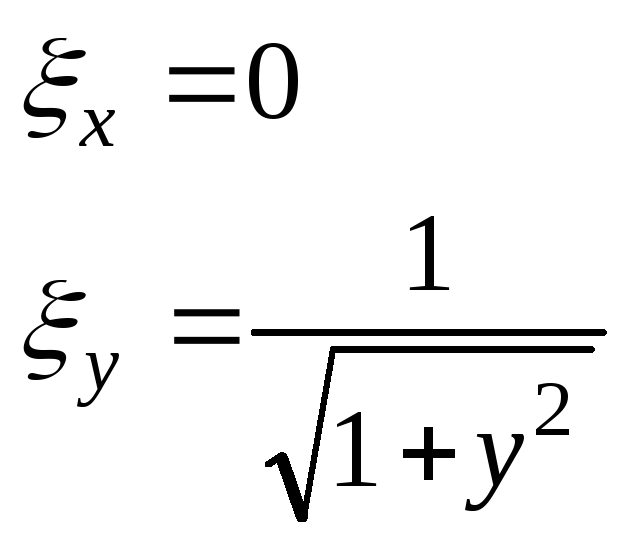
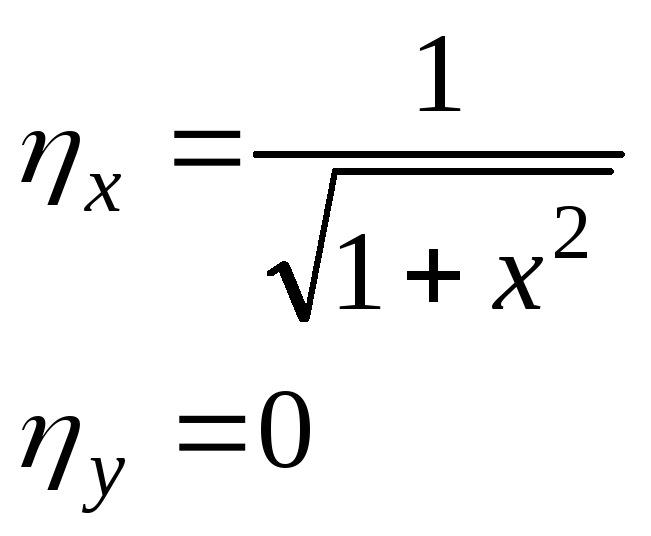
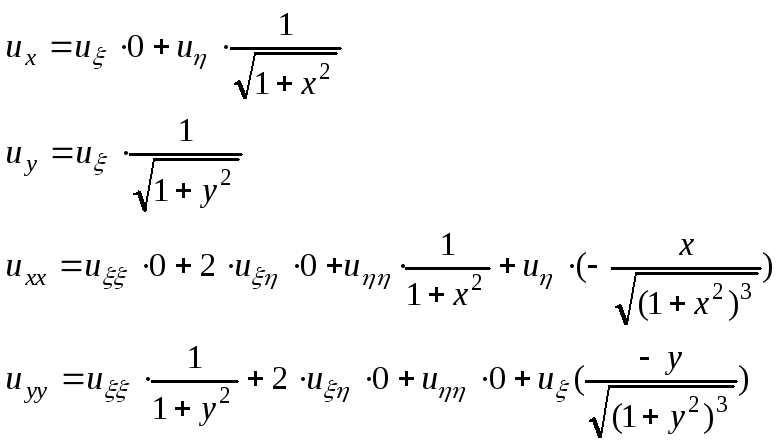
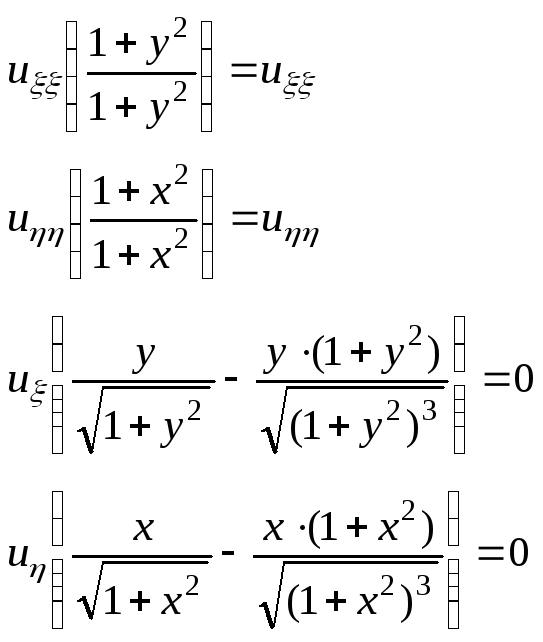
Ответ: -канонический вид

21. . Решить методом характеристик уравнение

А)

-гипербалич. тип

;

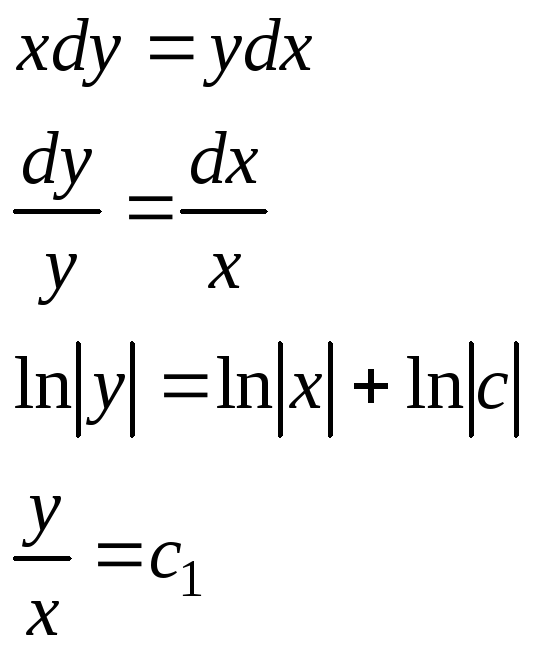
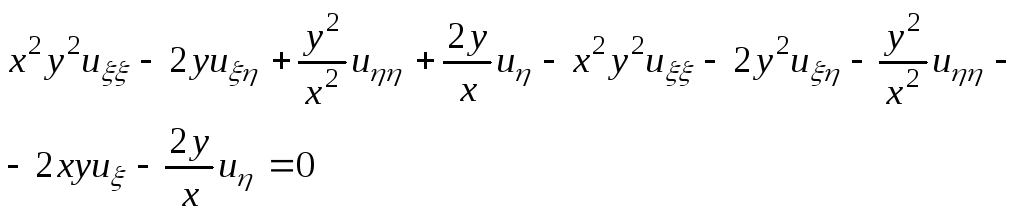
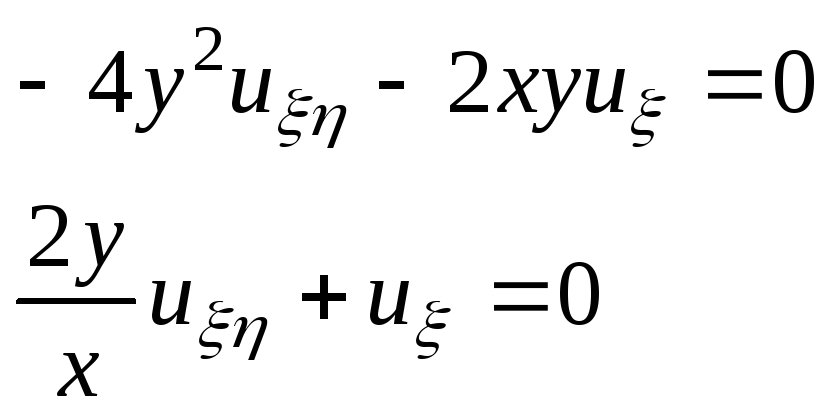
Пусть

; ;

;

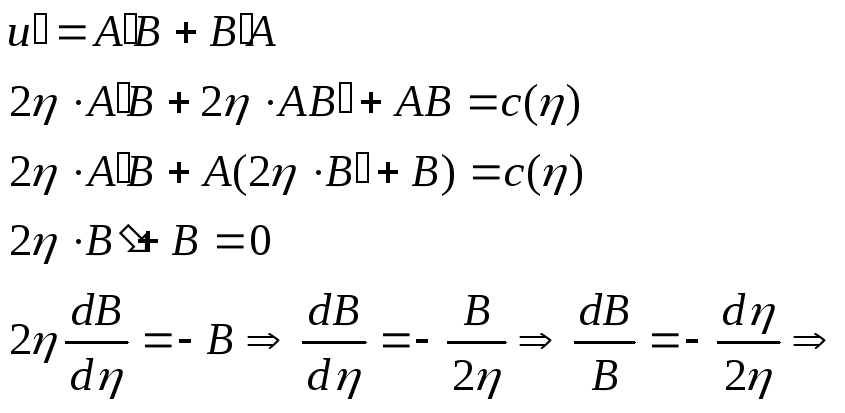
Следовательно

22 найти общее решене

А)

Частное решение ищем

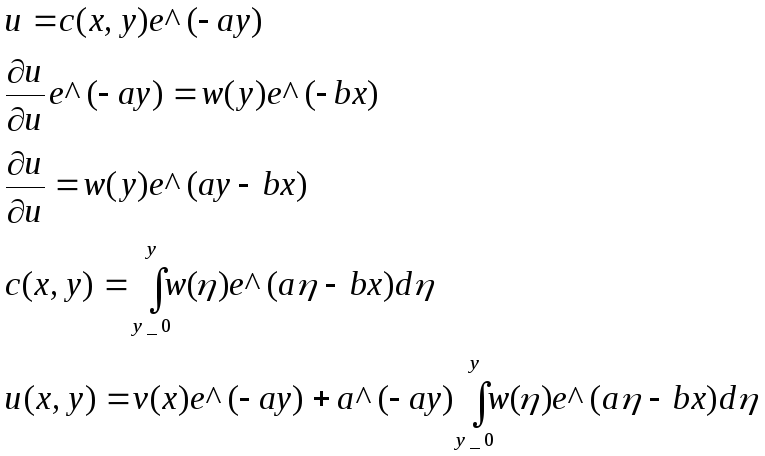
Б)

Общее и частное решение находится так же как в а)

а=-2,b=-3

23. В круге решить задачу Дирихле для уравнения Пуассона