Файл: Матан(Блок 1).doc

Пусть функции определены на X, все непрерывны в некоторой точке. Если ряд на множестве X сходится равномерно, то и сумма ряда в точке также будет непрерывна.

В.6. Криволинейный интеграл. Формула Грина.

1) Рассмотрим на плоскости некоторую кривую AB, гладкую или кусочно – гладкую.[Кривая, заданная уравнениями , называется гладкой, если функции и непрерывные производные и, не обращающиеся в ноль одновременно. Непрерывная кривая, составленная из конечного числа гладких кусков, называется кусочно - гладкой], и предположим, что функция определена и ограничена на кривой AB.

Разобьем кривую AB произвольно на n частей точками , выберем на каждой из частичных дуг произвольную точку и составим сумму (1), - длина дуги . Сумма (1) называется интегральной суммой для функции по кривой AB. Обозначим ч/з наибольшую из длин частичных дуг .

Опр. Если интегральная сумма (1) при имеет предел, равный I, то этот предел называется криволинейным интегралом первого рода от функции по кривой AB и обозначается одним из следующих символов . В этом случае функция называется интегрируемой вдоль кривой AB, сама кривая AB – контуром интегрирования, A – начальной, а B – конечной точками интегрирования.

Геометрический смысл.

Криволинейный интеграл при численно равен площади участа цилиндрической поверхности с образующей параллельной оси . Снизу этот участок ограничен контуром , а сверху кривой, изображающей подынтегральную функцию .

Вычисление криволинейного интеграла первого рода.

Вычисление криволинейного интеграла первого рода сводится к вычислению определённых интегралов. Пусть кривая AB задана параметрическими уравнениями , где и непрерывные, и - непрерывные, - функция, непрерывная вдоль этой кривой, причем в точке A:, в точке B: . Тогда для любой точке кривой AB длину дуги AM можно рассматривать как функцию параметра и вычислять по формуле откуда . Получаем:

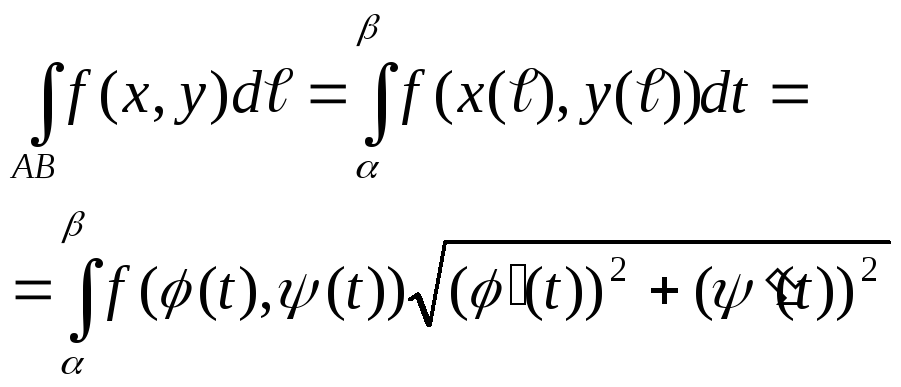
2) Пусть на кривой AB определены 2 ограниченные функции и . Разобьём кривую AB на n частей точками . Обозначим ч/з и проекции вектора на оси координат, на каждой частичной дуге возьмем произвольную точку и составим интегральную сумму для функции (): 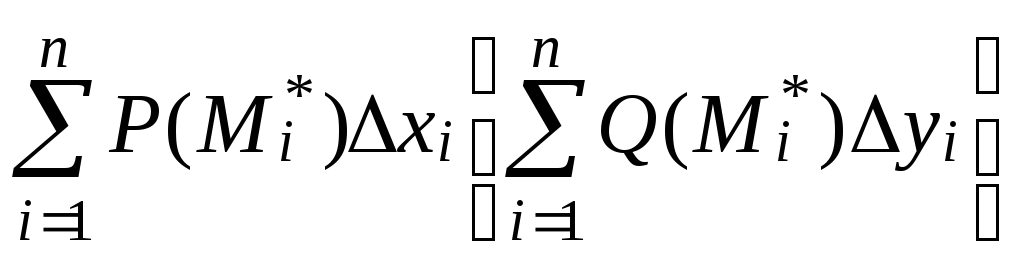(2).

Опр. Если интегральная сумма (2) при - длина дуги имеет предел I , то этот предел называется криволинейным интегралом второго рода от функции () по кривой AB и обозначается: .

Сумма называется общим криволинейным интегралом второго рода.

Вычисление криволинейного интеграла второго рода.

Криволинейные интегралы второго рода вычисляют сведением их к определённым интегралам по формулам:

;

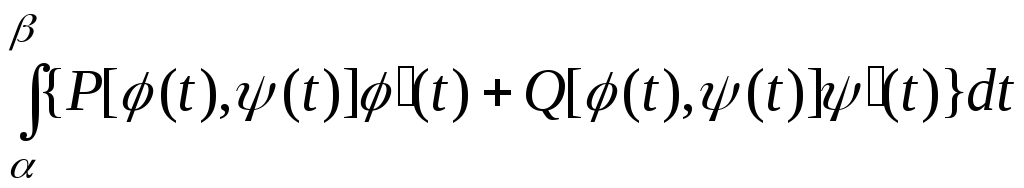= (3)

Где кривая AB: ; A:, B: .

В частности, если кривая AB задана уравнением вида , где y(x) – непрерывно дифференцируемая функция, то: , ; (4)

3) Формула Грина.

Т. Пусть G – некоторая простая замкнутая область, ограниченная контуром L, и пусть функции и непрерывны вместе со своими частными производными и в данной области. Тогда имеет место формула :

, называемая формулой Грина.

В.7. Производная функции комплексного переменного. Геометрический смысл аргумента и модуля производной. Условия Коши – Римана. Аналитическая функция.

Пусть в области комплексной плоскости z задана функция f(z). Если для точки существует при предел разностного отношения , то этот предел называется производной функции f(z) по комплексной переменной в точке и обозначается , т.е. (1)

Функция f(z) в этом случае называется дифференцируемой в точке .

Т.1. Если функция дифференцируема в точке , то в точке существуют частные производные функций и по переменным , причем имеют место следующие соотношения:

(2) – условие Коши – Римана.

Т.2. Если в точке функции и дифференцируемы, а их частные производные связаны соотношениями (2), то функция является дифференцируемой функцией комплексной переменной z в точке .