Файл: Матан(блок2).doc

Пусть ф-ии и и их частные производные первого порядка непрерывны в вплоть до , частные производные второго порядка внутри непрерывны и ограничены. Полагая и пользуясь формулой (1) приходим к первой формуле Грина (2).

Меняя местами u и v в формуле (2) будем иметь (3).

Вычитая (2) из (3) получим вторую формулу Грина (4).

Лемма. Если функция непрерывна, имеет непрерывные производные первого и второго порядка везде в области , причем первые производные непрерывны вплоть до границы, а вторые производные непрерывны внутри области, то имеет место формула:

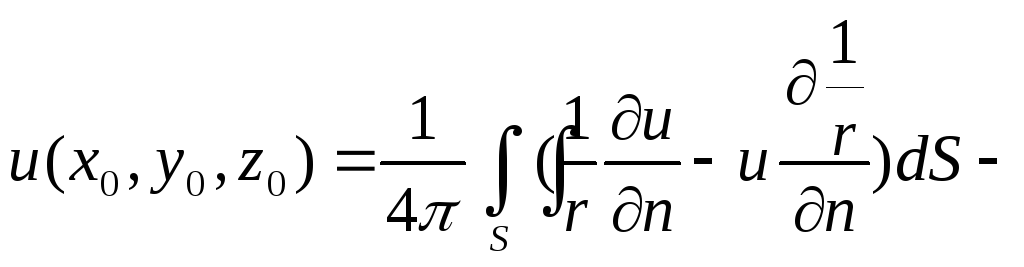
(5) где - расстояние от фиксированной точки лежащей внутри , до переменной точки , n – внешняя нормаль к поверхности .

Пусть гармоническая функция внутри конечной области - непрерывна вместе с производными первого порядка вплоть до границы области . Пусть известна ф-ия обладающая свойствами: 1) как функция переменной точки М она является гармонической внутри области и имеет непрерывные первые производные вплоть до поверхности ; 2) на поверхности ф-ия принимает граничные значения .

Функцией Грина задачи Дирихле для уравнения Лапласа называется ф-ия удовлетворяющая следующим условиям: 1) как функция точки М есть гармоническая внутри области исключая точку где она обращается в бесконечность; 2) она удовлетворяет граничному условию (6) ; 3) в области ф-ия допускает представление (7), где .