Файл: Матан(блок2).doc

Причем,ф-ия f_ε≥0 и (3).Решение этой задачи обозн-т у_ε(х,ξ). Интегрир ур-ия(1) с таким обр зад ф-ей по отр [ξ-ε, ξ+ε] получим

1(т.к.интегр=1)(4)

Предп,что предельная ф-ия сущ-ет и непрер на [0,l],тогда совершая пред-й переем при ε ->0 в (4) получим,что производная в точке х=ξ должна иметь разрыв 1го рода,причем разность пр и левого пред-го знач-ия этой произв-ой в точке х=ξ опред выр-м -.Т.о. если ф-ия сущ-ет,то она подчин-ся след-м усл-ям:1)как ф-ия перем-ой х удовл однор ур-ию при 0<x<ξ,ξ<x<l;2) удовл-ет гран-м усл-ям (1);3) непрер на [0,l],а ее первая произв-ая в точке х=ξ имеет разрыв 1го рода с велич-й скачка предельн знач =

ОпрФ-ию,удовл усл (1-3) наз-т функцией Грина первой краевой задачи.

Существенное значение ф-ии Грина закл в том,что что через нее м.б. выражено реш-е первой краевой задачи с произв правой частью f(x).Пусть сущ-ет реш-е зад(1) и ф-ия Грина .Примен форм-лу Грина

= к этим ф-м на отр [0,ξ-ε] и [ξ+ε,l],где ф-ии y(x) и непрер диф-мы и обл-т 2мя непрер произв,получим

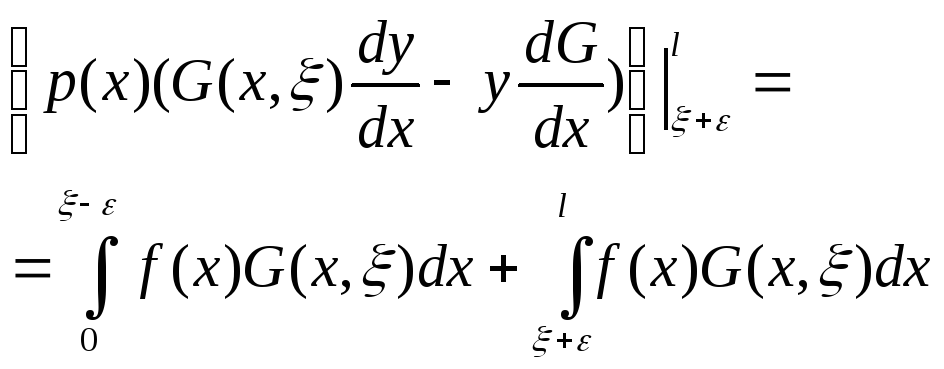+(5)

Т.к. ф-ии у(х) и удовл однородн граничн усл-я (1),то подст-ки х=0 и х=l обращ-т в нуль.Переходя в (5) к пределу всилу опред ф-ии Грина получим ,что и т.д.

13 Задача Штурма –Лиувилля

Имеет вид

Где q(x) – действительная непрерывная функця на некотором отрезке [a,b]

произвольные действительные числа

Лемма1

Если функции положительны в каждой точке отрезка [a,b]

То функция является решением дифференциального уравнения

Тогда и только тогда, когда функция

является решением уравнения

Где

Доказательство

Если функция то и функция

И наоборот если то функция

Учитывая равенства

Получаем

Осталось воспользоваться равенством

Лемма2

Если на [a,b] то уравнение

Эквивалентно уравнению

где

Доказательство

Очевидно что

Так как

То коэффициент при равен нулю то есть

Следовательно

Б.2 в. 14 Корректность постановки задач математической физики. Привести пример.

Так как задачи мат физики представляют собой мат модели реальных физических процессов то их постановки должны удовлетворять следующим естественным требованиям: 1) решение должно существовать в каком-либо классе функций , 2) решение должно быть единственным в каком-либо классе функций , 3) решение должно непрерывно завесить от данных задачи (начальных и граничных данных, свободного члена, коэффициентов ур-ия).

Непрерывная зависимость решения u от данных задачи D означает следующее: пусть последовательность данных , k=1,2,… в каком-то смысле стремится к D , и k=1,2,… соответствующее решения задачи; тогда должно быть в смысле надлежащим образом выбранной сходимости. Например пусть задача приводится к уравнению где L – линейный оператор, переводящий M в N, где M и N – линейные нормированные пространства. В этом случае непрерывная зависимость решения u от свободного члена F будет обеспечена если оператор существует и ограничен из N в М. требование непрерывной зависимости обуславливается тем обстоятельством что физические данные как правило определяются из эксперимента приближенно и поэтому нужно быть уверенным в том что решение задачи в рамках выбранной мат модели не будет существенно зависеть от погрешностей измерений.

Задача удовлетворяющая перечисленным требованиям называется корректно поставленной (по Адамару), а множество функций наз-ся классом корректности. Задача не удовлетворяющая хотя бы одному из условий 1)-3) наз-ся некорректно поставленной.

К некорректно поставленным задачам часто приводят обратные задачи мат физики: по некоторой информации о решении прямой задачи восстановить некоторые неизвестные физические величины, определяющие эту задачу (источники, краевые условия, коэффициенты уравнения и др.).

15

Дифференциальным уравнением называется уравнение, содержащие производные неизвестных функций.

Если неизвестная функция зависит от одной переменной, то это уравнение называетсяобыкновеннвм диф ур-ем, в противном случае- ур-ем в частных производных. Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.

Частной производной первого порядка функции u([) по переменной х_i называется предел