Файл: Матан(блок2).doc

Дифференциальным уравнением с частными производные относительно неизвестн функции u(x) называется отношение

Введем сокращенное обозначение , где L- дифференц оператор, действующий на функцию и преобразующий их в элементы пространства непрерывных функций .

Уравнение вида , где множеству непрерывных функций, называется линейным дифференциальным уравнением с частными производными, если для диф оператора L выполнены условия линейности

1)

2)

Рассмотри класс уравнений второго порядка с двумя неизвестными переменными. Введем специальные обозначения независ перем тогда

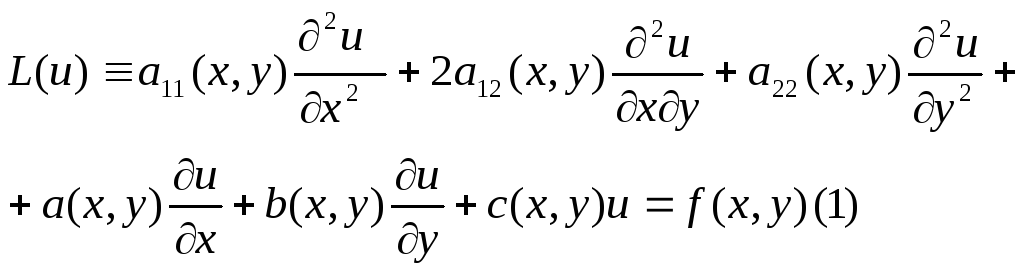
- заданные функции двух переменных

неизвестная функция

Для классификации уравнений (1), построим вспомогательную функцию

называемой дискриминантом уравнения.

Определение Тип уравнения определяется следующим образом

1) >0, то (1) называется гиперболического типа

2) <0-эллиптического типа

3) =0-параболического в точке (х,у)

Примера:

1. гиперболич тип – уравнение колебание струны 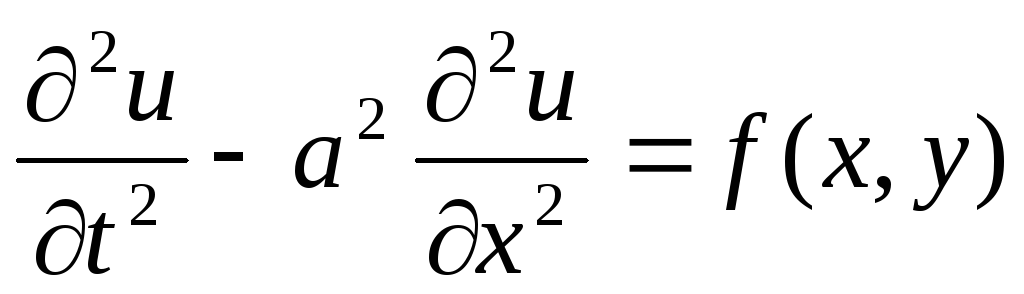, где

х=х₁пространственная переменная, t=х₂- временная переменная.

2) эллиптический тип- Уравнение Лапласа ; х,у- пространственная переменная

3) параболическое уравнение-уравнение теплопроводности

Перейдем в уравнении (1) от неизвестных переменных х, уК новым независимым переменным с помощью невырожденного преобразования

(2)

Преобразование (2) называется невырожденным в Е, если якобиан

Преобразуем производные к новым переменным

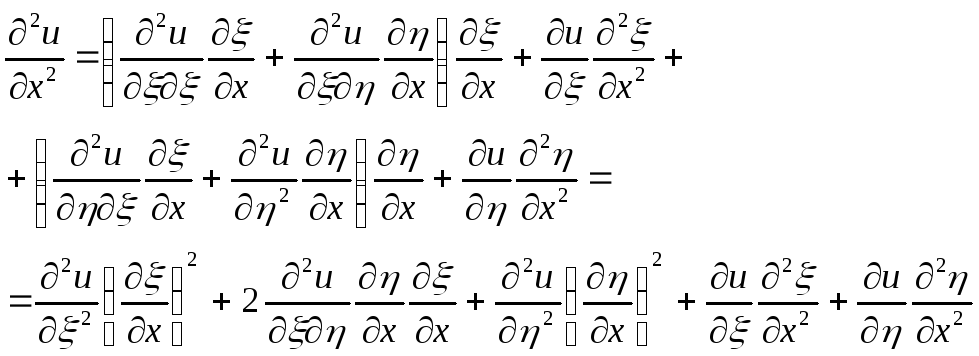
(3) Подставляя значения производных из (3) в (1) будем иметь

(4)

где

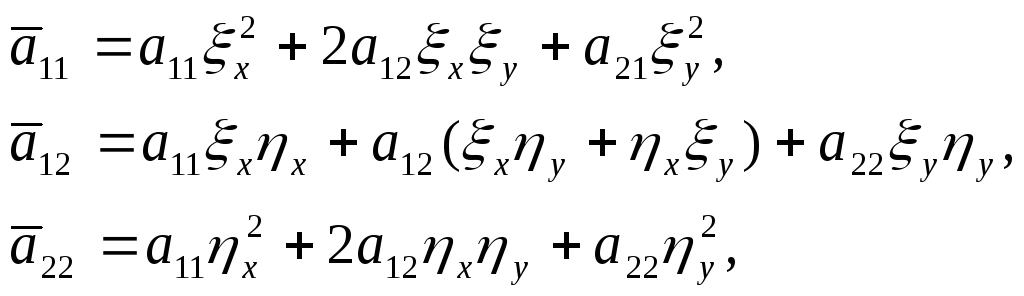
функция не зависит от вторых производных.

Выберем переменные таким образом, чтобы коэффициент был равен нулю. Рассмотрим уравнение с частн производными первого порядка

(5)

Пусть -какое нить частное решение этого уравнения. Если положить то , таким образом задача о выборе новых неизвестных переменных связана с решением уравнения (5).

Лемма: Если является частным решением уравнения , то соотношение представляет собой общий интеграл обыкновенного диф уравнения

(6)

Уравнение (6) называется характеристическим уравнением для уравнения (1), а его интегралы- характеристиками.

Уравнеине (6) распадается на 2 уравнения:

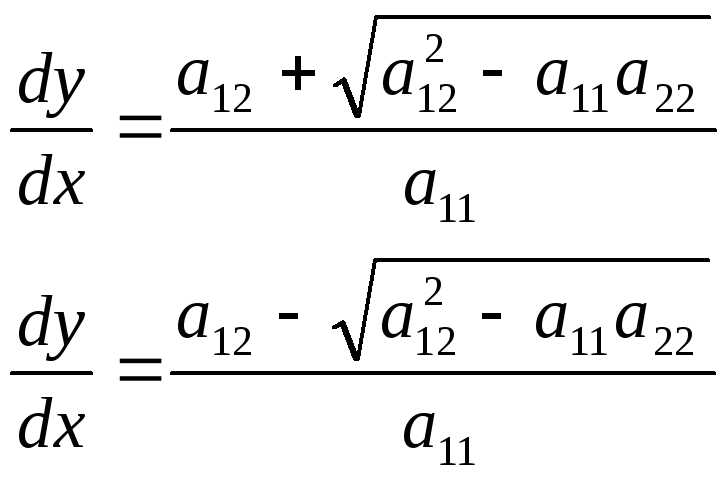
А подкоренное выражение определяет тип уравнения (1)

1) Пусть >0 (гиперболический тип)

Канонич вид тогда будет

2. Пусть 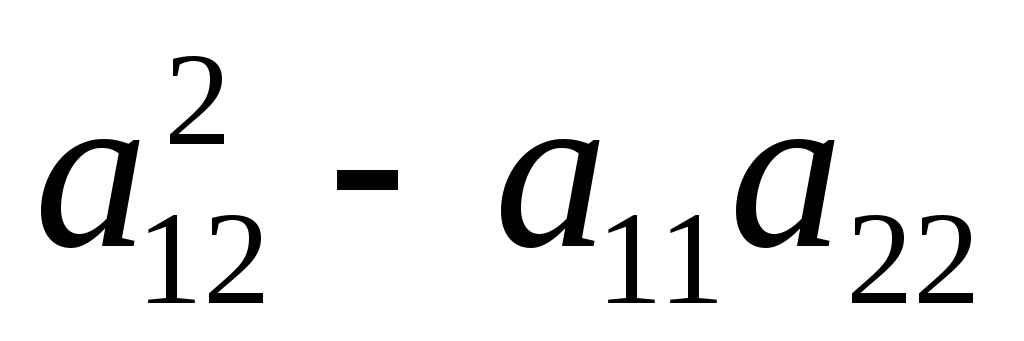=0 (параболический тип)

Канония вид

3)

Пусть <0 (элиптич тип )

Б.2 в. 16 Первая краевая задача для Ур колебания струны. Интеграл энергии и единственности решения первой краевой задачи.

Рассмотрим уравнение (1) описывающие поперечные колебания струны. (Если рассматриваются свободные колебания струны то они описываются ур-ем ).

Сформулирует первую краевую задачу для ур-ия (1). Найти ф-ию определенную в области удовлетворяющую ур-ию для 0<x<l, t>0, граничным t>0 (2) и начальным условиям 0<x<l (3).

Теорема единственности: Возможно существование только одной ф-ии определенной в области и удовлетворяющей уравнению (4) начальным и граничным условиям: (5) если выполнены условия: 1) ф-ия и производные входящие в ур-ие (4) а также производная непрерывны на отрезке ; 2) коэффициенты и k(x) непрерывны на отрезке .

Д-во: допустим существует два решения рассматриваемой задачи и и рассмотрим разность . Ф-ия очевидно удовлетворяет однородному уравнению и однородным дополнительным условиям: ; а также условию 1) теоремы. Докажем что . Рассмотрим ф-ию (6) и покажем что она не зависит от t.

Ф-ия (6) называется полной энергией струны. Физический смысл ф-ии E(t): это полная энергия струны в момент времени t.

Продифференцируем E(t) по t, выполняя при этом дифференцирование под знаком интеграла: . Интегрируя по частям первое слагаемое правой части будем иметь: . Подстановка обращается в нуль в силу граничных условий (из следует и аналогично для x=l). Отсюда следует что т.е. E(t)=const. учитывая начальные условия получаем (7) т.к.

. Пользуясь формулой (7) и положительностью k и заключаем, что . Откуда и следует тождество . Пользуясь начальным условием, находим ,тем самым доказано что . Следовательно если существуют две функции и удовлетворяющие всем условиям теоремы то .