ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.04.2024
Просмотров: 146
Скачиваний: 0
СОДЕРЖАНИЕ
Б. 2 в. 1 Необходимые условия экстремума функции нескольких переменных. Достаточные условия
4.Формула Тейлора с остаточным членом в форме Лагранжа. Разложение элементарных функций.
Б.2 в. 5 Ряд Лорана. Классификация изолированных особых точек. Вычеты.
8 Теорем Рисса о представлении линейного функционала
Б.2 в. 14 Корректность постановки задач математической физики. Привести пример.
Дифференциальным уравнением называется уравнение, содержащие производные неизвестных функций.
Б.2 в.19 Функция Грина. Функция Грина для внутренней задачи Дирихле.
Представляя
многочлен
![]() в виде (2), получим:
в виде (2), получим:
![]() ,
,
![]() ,
…,
,
…,
![]() .
Т.о. мы получили, что построенный
формальный многочлен
.
Т.о. мы получили, что построенный
формальный многочлен
![]() и его производные в точке
и его производные в точке
![]() совпадают со значениями ф-ии
совпадают со значениями ф-ии
![]() и её производными. Если
и её производными. Если
![]() -есть
многочлен степени
-есть
многочлен степени
![]() ,
то
,
то
![]() .
Если же
.
Если же
![]() не есть многочлен или является многочленом
степени выше
не есть многочлен или является многочленом
степени выше
![]() ,
то подобное рав-во не имеет смысла. В
этом случае многочлен
,
то подобное рав-во не имеет смысла. В
этом случае многочлен
![]() лишь приближённо представляет ф-ию
лишь приближённо представляет ф-ию
![]() в точке
в точке
![]() .
Разность
.
Разность
![]() .
Тогда очевидно будет погрешностью
допускаемой при замене
.
Тогда очевидно будет погрешностью
допускаемой при замене
![]() на
на
![]() .
Т.о.
.
Т.о.
![]() (3).
Это тоже ф-ла Тейлора. Слагаемое
(3).
Это тоже ф-ла Тейлора. Слагаемое
![]() обычно наз. Либо
дополнительным, либо остаточным членом.
Дополнительным
к ф-ле (2) и остаточным к
обычно наз. Либо
дополнительным, либо остаточным членом.
Дополнительным
к ф-ле (2) и остаточным к
![]() до
до
![]() .
.
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
Б.2 в. 5 Ряд Лорана. Классификация изолированных особых точек. Вычеты.
Рассмотрим ряд
вида
![]() (1)
где
(1)
где
![]() фиксированная точка комплексной
плоскости,
фиксированная точка комплексной
плоскости,
![]() некот комплексное число, а суммирование
ряда ведется как по полож так и по отриц
значениям индекса n.
Ряд (1) носит название ряда
Лорана.
некот комплексное число, а суммирование
ряда ведется как по полож так и по отриц
значениям индекса n.
Ряд (1) носит название ряда
Лорана.
Теорема:
ф-ия
![]() аналитическая
в круговом кольце
аналитическая
в круговом кольце
![]() однозначно
представляется в этом кольце сходящимся
рядом Лорана.
однозначно
представляется в этом кольце сходящимся
рядом Лорана.
Если
![]() диф-ма во всех точках некот области
G
а ее производная
непрерывна в этой области то ф-ия
диф-ма во всех точках некот области
G
а ее производная
непрерывна в этой области то ф-ия
![]() наз аналитической
в области G.
наз аналитической
в области G.
Точка
![]() наз изолированной
особой точкой
ф-ии
наз изолированной
особой точкой
ф-ии
![]() если
если
![]() однозначная и аналитичная в круговом
кольце
однозначная и аналитичная в круговом
кольце
![]() а точка
а точка
![]() является особой точкой ф-ии
является особой точкой ф-ии
![]() .
.
Пусть ф-ия
![]() задана в области G,
ограниченном контуром Г. Точка
задана в области G,
ограниченном контуром Г. Точка
![]() наз-ся
правильной точкой ф-ии
наз-ся
правильной точкой ф-ии
![]() если существует сходящийся степенной
ряд
если существует сходящийся степенной
ряд
![]() ,
кот в общей части области G
и своего круга сходимости
,
кот в общей части области G
и своего круга сходимости
![]() сходится к ф-ии
сходится к ф-ии
![]() ,
,
![]() .
Точки
.
Точки
![]() не являющиеся правильными точками ф-ии
не являющиеся правильными точками ф-ии
![]() наз-ся особыми
точками.
наз-ся особыми
точками.
В основу квалификации
изолированных особых точек однозн ф-ии
![]() положен способ ее разложения в окрестности
таких точек.
положен способ ее разложения в окрестности
таких точек.
1 тип.
Разложение (1) не содержит отриц степеней
![]() .
В этом случае точка a
наз-ся устранимой
особой точкой
ф-ии
.
В этом случае точка a
наз-ся устранимой
особой точкой
ф-ии
![]() т.е.
ряд (1) обращается в обыкновенный степенной
ряд и следовательно сходится всюду в
окрестности точки a,
включая точку a.
Сумма этого ряда будет представлять
собой ф-ию голоморфную в окрестности
точки a.
Данная ф-ия
т.е.
ряд (1) обращается в обыкновенный степенной
ряд и следовательно сходится всюду в
окрестности точки a,
включая точку a.
Сумма этого ряда будет представлять
собой ф-ию голоморфную в окрестности
точки a.
Данная ф-ия
![]() совпадает
с суммой ряда если
совпадает
с суммой ряда если
![]() .
Поэтому мы сделаем
.
Поэтому мы сделаем
![]() голоморфной в точке a,
если положим
голоморфной в точке a,
если положим
![]() .
Таким образом особая точка этого типа
исчезает, если мы надлежащим образом
определим нашу ф-ию в этой точке. Сл,
если точка a
устранимая особая точка то
.
Таким образом особая точка этого типа
исчезает, если мы надлежащим образом
определим нашу ф-ию в этой точке. Сл,
если точка a
устранимая особая точка то
![]() т.е.
т.е.
![]() в малой окрестности устранимой точки
ф-ия ограничена.
в малой окрестности устранимой точки
ф-ия ограничена.
2 тип.
Разложение (1) содержит конечное число
отриц степеней
![]() .
В этом случае точка a
наз-ся полюсом
ф-ии
.
В этом случае точка a
наз-ся полюсом
ф-ии
![]() .
Если обозначить через m
наиб из отриц степеней, входящих в
разложение (1) то получим
.
Если обозначить через m
наиб из отриц степеней, входящих в
разложение (1) то получим
![]() .
Если m=1
то полюс наз простым,
при m>1
полюс наз кратным,
а m
наз порядком
полюса. В
окрестности полюса ф-ия не ограничена.
.
Если m=1
то полюс наз простым,
при m>1
полюс наз кратным,
а m
наз порядком
полюса. В
окрестности полюса ф-ия не ограничена.
3 тип.
Разложение (1) содержит бесконечное
множество отрицательных степеней
![]() .
В этом случае точка a
наз существенно
особой точкой ф-ии
.
В этом случае точка a
наз существенно
особой точкой ф-ии
![]() .
.
Теорема (Сохотского): какую бы малую окрестность существенно особой точки мы ни взяли, ф-ия в ней не ограничена и принимает значения как угодно мало отличающиеся любого наперед заданного числа.
Мероморфной ф-ей называют всякую однозначную ф-ию, не имеющую в конечной части плоскости других особых точек кроме полюсов.
Ф-ия голоморфна
если ее можно разложить в ряд Тейлора
по степеням
![]() .
.
Вычет в конечной
точке. Пусть
![]() аналит в кольце
аналит в кольце
![]() .
Тогда точка a
явл для ф-ии
.
Тогда точка a
явл для ф-ии
![]() изолированной особой точкой а ф-ия
изолированной особой точкой а ф-ия
![]() представима в кольце сходящимся рядом
Лорана
представима в кольце сходящимся рядом
Лорана
![]() .
Вычетом
ф-ии
.
Вычетом
ф-ии
![]() в точке a
наз коэффициент
в точке a
наз коэффициент
![]() ряда Лорана для
ряда Лорана для
![]() в окрестности точки а.
Обозначается
в окрестности точки а.
Обозначается
![]()
![]() где
где
![]()
![]()
Вычет в полюсе
![]() .
Если а
простой вычет
.
Если а
простой вычет
![]() то ряд Лорана в окрестности точки а
имеет след вид:
то ряд Лорана в окрестности точки а
имеет след вид:
![]()
![]() .
В частности
.
В частности
![]() где
где
![]() -
голоморфные в точке а, причем
-
голоморфные в точке а, причем
![]()
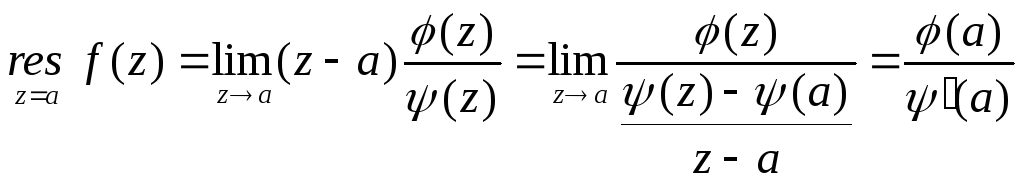 . Если a
кратный полюс то
. Если a
кратный полюс то
![]() .
.
Вычет бесконечно
удаленной точки.
Пусть
![]() голоморфна в области
голоморфна в области
![]() следовательно точка
следовательно точка
![]() является изолированной особой точкой
а ф-ия
является изолированной особой точкой
а ф-ия
![]() представима в этой области сходящимся
рядом Лорана
представима в этой области сходящимся
рядом Лорана
![]() .
Вычетом ф-ии
.
Вычетом ф-ии
![]() в точке
в точке
![]() называется число
называется число
![]() где
где
![]() коэффициент ряда Лорана при
коэффициент ряда Лорана при
![]()
для ф-ии
![]() в окрестности бесконечно удаленной
точки, т.е.
в окрестности бесконечно удаленной
точки, т.е.
![]() т.е.
т.е.
![]() ;
;
![]()
Теорема (основная
теорема вычетов):
пусть ф-ия
![]() голоморфна в каждой точке
голоморфна в каждой точке
![]()
Кроме конечного
числа особых точек
![]() .
Обозначим
.
Обозначим
![]() произвольный кусочно-гладкий замкнутый
контур, содержащий внутри себя точки
произвольный кусочно-гладкий замкнутый
контур, содержащий внутри себя точки
![]() и целиком лежащий в области (D).
При этих условиях
и целиком лежащий в области (D).
При этих условиях
![]() равен сумме вычетов ф-ии
равен сумме вычетов ф-ии
![]() относительно точек
относительно точек
![]()
![]()
№6. Опр1 Отображение g метрич-го простр-ва (X,ρ) наз-ся сжимающим,
если сущ-ет такое число 0<α<1,что ρ(g(x),g(y))≤ αρ(x,y).
Теорема1(принцип сжимающих отображений)
Всякое сжимающее
отобр-е полного метрич-го простр-ва
(X,ρ)в
это же простр-во имеет и при том только
одну неподв-ую точку х![]() Х,т.е.такую
точку х
Х,т.е.такую
точку х![]() Х,что
g(x)=x.
Х,что
g(x)=x.
Опр2
2 отобр-ия g
и g1
метрич-го простр-ва(X,ρ)
в это же простр-во коммутируют,если(![]() )
)![]()
Теорема2 (обобщение принципа сжатых отобр-ий)
Пусть g и g1 отобр-ие полного метрич-го простр-ва (X,ρ)в это же простр-во,
тогда если отобр-е
g1
сжимающ и отобр g
и g1
коммутируют,то ур-ие g(x)=x
имеет решение х![]() Х.
Х.