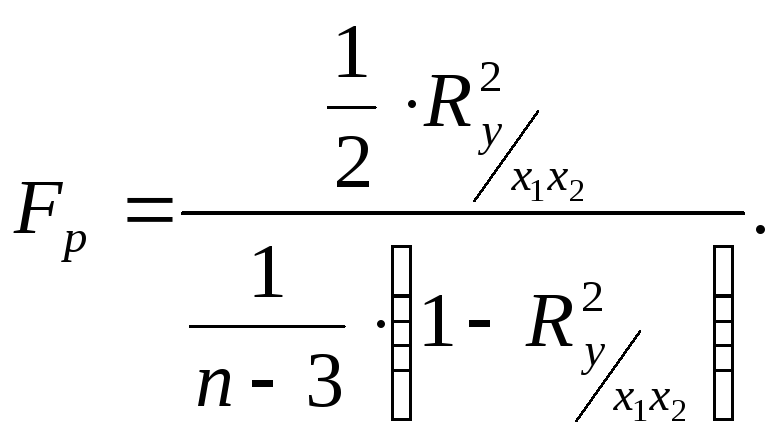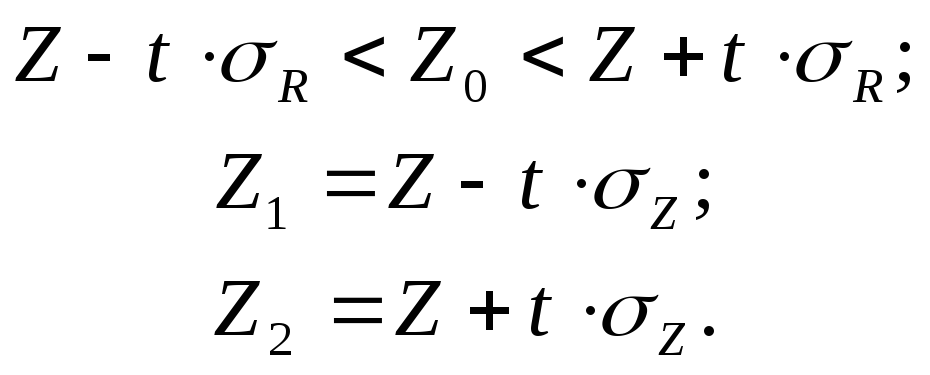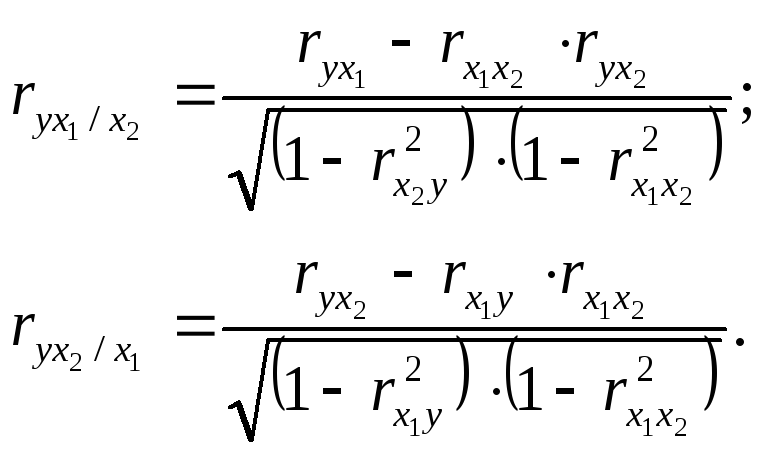Файл: Тема 9.doc

где

коэффициенты в стандартизованном масштабе.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .

Приближение к единице свидетельствует о сильной зависимости между признаками. При небольшом числе наблюдений величина коэффициента множественной корреляции, как правило, завышается.

Чтобы оценить общую вариацию результативного (моделируемого) признака в зависимости от факторных признаков, величина коэффициента множественной корреляции корректируется на основании следующего выражения:

(9.34)

где		скорректированное значение;
		число наблюдений;
		число факторных признаков.

Корректировка не производится при условии, если

Проверка значимости коэффициента множественной корреляции осуществляется на основе -критерия Фишера-Снедекора:

(9.35)

---

Гипотеза о незначимости коэффициента множественной корреляции () отвергается, если.

Оценка доверительных границ производится следующим образом: величина приравнивается к гиперболическому тангенсу величины, т.е., где

Плотность распределения является почти нормальной со средним значением

(9.36)

и дисперсией

Следовательно,

отсюда:

(9.37)

По таблицам -преобразования Фишера находят и, т.е. - верхняя и нижняя границы значений.

Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признакамии при фиксированном значении других () факторных признаков, т.е. когда влияниеисключается и оценивается связь междуив «чистом виде».

---

Коэффициент, в котором исключается влияние только одного факторного признака, называется коэффициентом частной корреляции первого порядка. В общем виде коэффициент корреляции первого порядка выражается так:

.

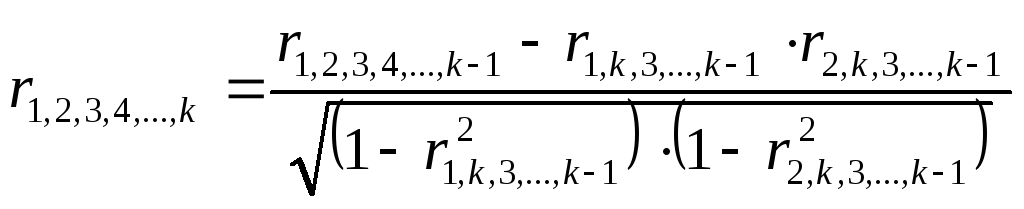В случае зависимости от двух факторных признаковикоэффициент частной корреляции следующий:

(9.38)

где

парные коэффициенты корреляции между указанными в индексе переменными.

В первом случае исключено влияние факторного признака , во втором- . Значения парного и частного коэффициентов корреляции отличаются друг от друга, так как парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный - учитывает наличие и влияние других факторов.

Проверка значимости и расчет доверительных интервалов для частных коэффициентов корреляции аналогичны расчетам для парных коэффициентов с тем лишь отличием, что число степеней свободы определяется как

где

порядок коэффициента частной корреляции.

Обобщенную методику корреляционного метода анализа экономических явлений и процессов можно представить блок-схемой (рис. 9.8).

---

---

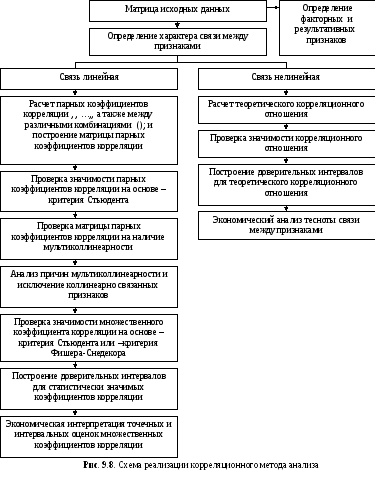
9.7 Методы изучения связи социальных явлений

Важной задачей статистики является разработка методики статистической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки.

Как правило, анализ социальных явлений, их связей и зависимостей должен начинаться с построения графиков связей. В настоящее время используются графики, характеризующие связь социальных явлений (рис. 9.9).

С помощью графика (рис. 9.9 а) «цепь» изображаются связи между социальными признаками, которые одинаково существенны и значимы.

График (рис. 9.9 б) «звезда» изображает зависимость социальных явлений, которые тяготеют к одному наиболее значимому. Исключение данного признака нарушает взаимосвязи между оставшимися признаками.

На графике (рис. 9.9 в) «сетка» выделяется несколько значимых признаков, которые тесно зависимы друг от друга.

Для количественной характеристики многомерных (многофакторных) связей социальных явлений используется метод корреляционных плеяд, основанный на расчете коэффициентов связи, которые носят общее названиеинформативных коэффициентов. Метод корреляционных плеяд позволяет сгруппировать взаимосвязанные признаки в так называемые плеяды. Плеяды выделяются на основе матрицы информационных коэффициентов корреляции, коэффициентов сопряженности и т.д. Алгоритм построения корреляционных плеяд базируется на выделении максимальных значений информационных коэффициентов в исходной матрице значений. На базе отдельно выделенных плеяд строится «дерево плеяд», особенность которого в том, что внутриплеядные связи между факторными признаками тесные, а межплеядные - слабые.

Информационной основой для такого анализа служат данные различных социологических обследований на базе анкетирования.

Вычисление информационных коэффициентов служит основой для дальнейшего углубленного анализа связей между социальными явлениями. В настоящее время такой углубленный статистический анализ проводится при разработке корреляционных плеяд с дальнейшим переходом к факторному анализу или методу главных компонент.

Количественная оценка связей социальных явлений осуществляется на базе расчета и анализа целого ряда коэффициентов.

При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд показателей.

---