Добавлен: 21.10.2018
Просмотров: 3249
Скачиваний: 12
43
4.2.2. Построение желаемой ЛАЧХ
Желаемая ЛАЧХ состоит из трёх участков.
Низкочастотный участок определяет точность работ САУ в
установившемся режиме, т.е. ее статические свойства. Для систем с порядком
астатизма γ=1 низкочастотный участок должен иметь наклон −20 дБ/дек. А при
ω=1 с
-1
ЛАЧХ должна иметь ординату равную 20∙lgk=20 дБ.
Среднечастотный участок определяет основные динамические свойства
САУ. Среднечастотный участок проводится с наклоном −20 дБ/дек, т. к. при
больших наклонах трудно обеспечить устойчивость системы и необходимое
перерегулирование. Протяженность этого участка устанавливаем исходя из
необходимого запаса устойчивости по амплитуде ∆L, т.е. не менее 11дБ
рекомендованного в [2].
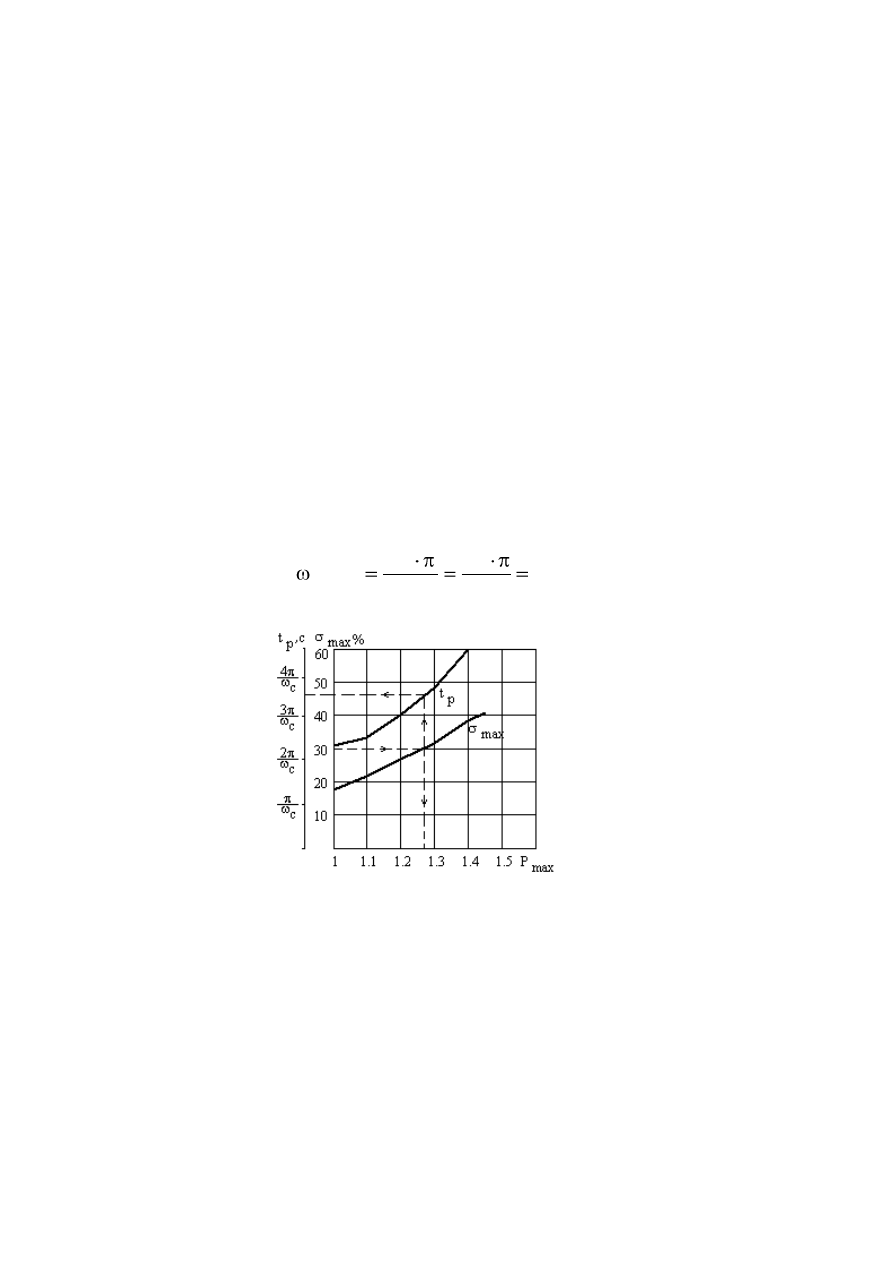
Определяем частоту среза. Для заданного σ
max
%≤30 % по номограмме,
связывающей показатели качества переходного процесса и параметры типовой
вещественной характеристики (рис.24), определяем P
max
=1,27. Тогда для
P
max
=1,27 по той же номограмме определяем t
р
=3,6∙π/ω
ср.
Откуда минимальная
частота среза желаемой ЛАЧХ может быть найдена по формуле:
52
,
4
5
,
2
6
,
3
t
6
,
3
max
р
min
ср
c
-1
.
Рис. 24 . Номограмма, связывающая показатели качества
переходного процесса и параметры типовой вещественной
характеристики
Максимальная частота среза желаемой ЛАЧХ выбирается из условия
обеспечения заданного ускорения отработки объектом регулирования
рассогласования ошибки с требуемой точностью. Так, при наличии начального
рассогласования ∆ε ускорение выходной координаты ограничивается
значением δ
в
'', при этом частота среза должна быть не более ω
срmax
. Тогда
максимальная частота среза может быть найдена по формуле:

44
10
1
,
0
10
в
max
ср
с
-1
.
Частота среза желемой ЛАЧХ выбирается в диапазоне: 4,52 c
-1
≤ω
ср
≤10 c
-1
.
Для получения более простой передаточной функции корректирующего звена
принимаем ω
ср
=10 c
-1
.
Высокочастотный участок определяет сглаживающие свойства системы
по отношению к помехам и на устойчивость и качество системы влияния не
оказывает.
Поэтому
высокочастотный
участок
логарифмической
характеристики имеет наклон, как и у неизменяемой части системы −60 дБ/дек.
В результате получим желаемую ЛАЧХ, передаточная функция которой
имеет вид:
.
)
1
s
04
,
0
(
)
1
s
06
,
0
(
s
10
)
s
(
W
ж
Определим устойчивость системы в замкнутом состоянии. Для этого
следует найти характеристическое уравнение замкнутой системы.
Передаточная функция замкнутой желаемой системы имеет вид:
.
10
s
1
s
1
,
0
s
10
24
10
)
s
(
W
1
)
s
(
W
)
s
(
W
2
3
4
ж
ж
жз
Откуда характеристическое уравнение замкнутой системы:
.
10
s
1
s
1
,
0
s
10
24
)
s
(
D
2
3
4
Коэффициенты характеристического уравнения равны:
a
0
=24∙10
-4
; a
1
=0,1; a
2
=1; a
4
=10.
Проверяем устойчивость системы по критерию Гурвица.
Т.к. а
0
>0, а
1
>0, а
2
>0, а
3
>0, то для устойчивости системы требуется
выполнение условия:
0
10
7
,
9
10
24
1
1
,
0
a
a
a
а
2
5
3
0
2
1
Следовательно, система устойчива.
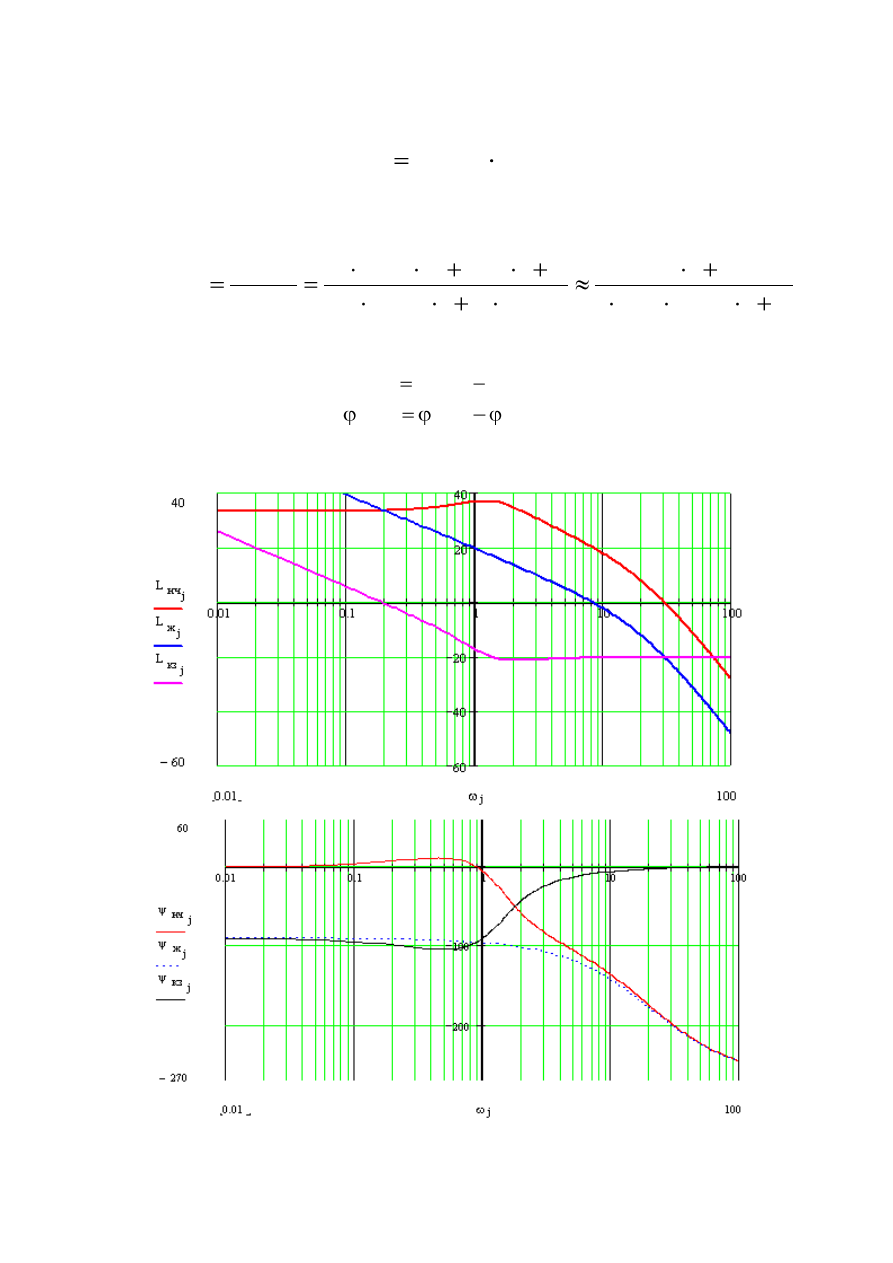
На рис. 25 представлены ЛАЧХ и ФЧХ желаемой системы.
45
4.2.3. Синтез передаточной функции корректирующего звена
Передаточная функция желаемой разомкнутой системы:
).
s
(
W
)
s
(
W
)
s
(
W
кз
нч
ж
Откуда передаточная функция последовательного корректирующего
звена может быть вычислена:
)
1
s
667
,
1
(
97
,
2
s
)
1
s
7
,
0
(
7
,
29
)
1
s
667
,
1
(
s
)
1
s
84
,
0
s
49
,
0
(
10
)
s
(
W
)
s
(
W
)
s
(
W
2
2
нч
ж
кз
ЛАЧХ и ФЧХ последовательного корректирующего звена:
);
s
(
L
)
s
(
L
)
s
(
L
нч
ж
кз
).
s
(
)
s
(
)
s
(
нч
ж
кз
ЛАЧХ и ФЧХ последовательного корректирующего звена изображены на
рис. 25.
Рис. 25 . Логарифмические амплитудные и фазовые частотные
характеристики исследуемой САУ.
46
4.2.4. Построение переходного процесса
Построим график переходного процесса на основе связи между
переходным процессом и вещественной частотной характеристикой замкнутой
системы, определяемой следующей зависимостью:
.
d
)
t
sin(
)
(
P
2
)
t
(
h
0
В свою очередь, вещественная характеристика замкнутой системы
вычисляется согласно определению:
)).
i
(
W
Re(
)
(
P
жз
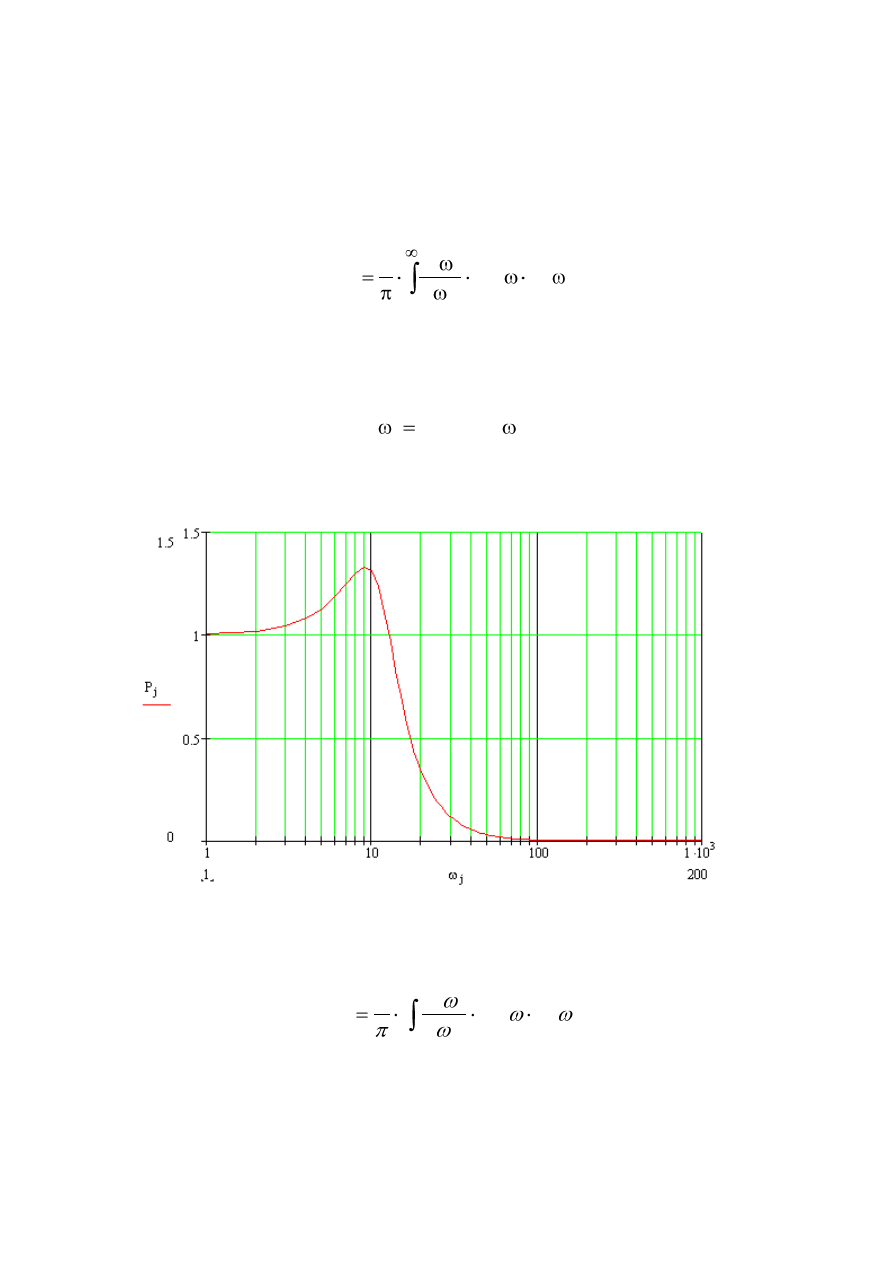
Вещественная частотная характеристика системы представлена на рис.26.
Рис. 26. Вещественная частотная характеристика
На основе вида вещественной характеристики переходный процесс может
быть построен по следующей функции:
d
t
P
t
h
120
0
)
sin(
)
(
2
)
(
Переходный процесс может быть построен также с использованием
обратного преобразования Лапласа.
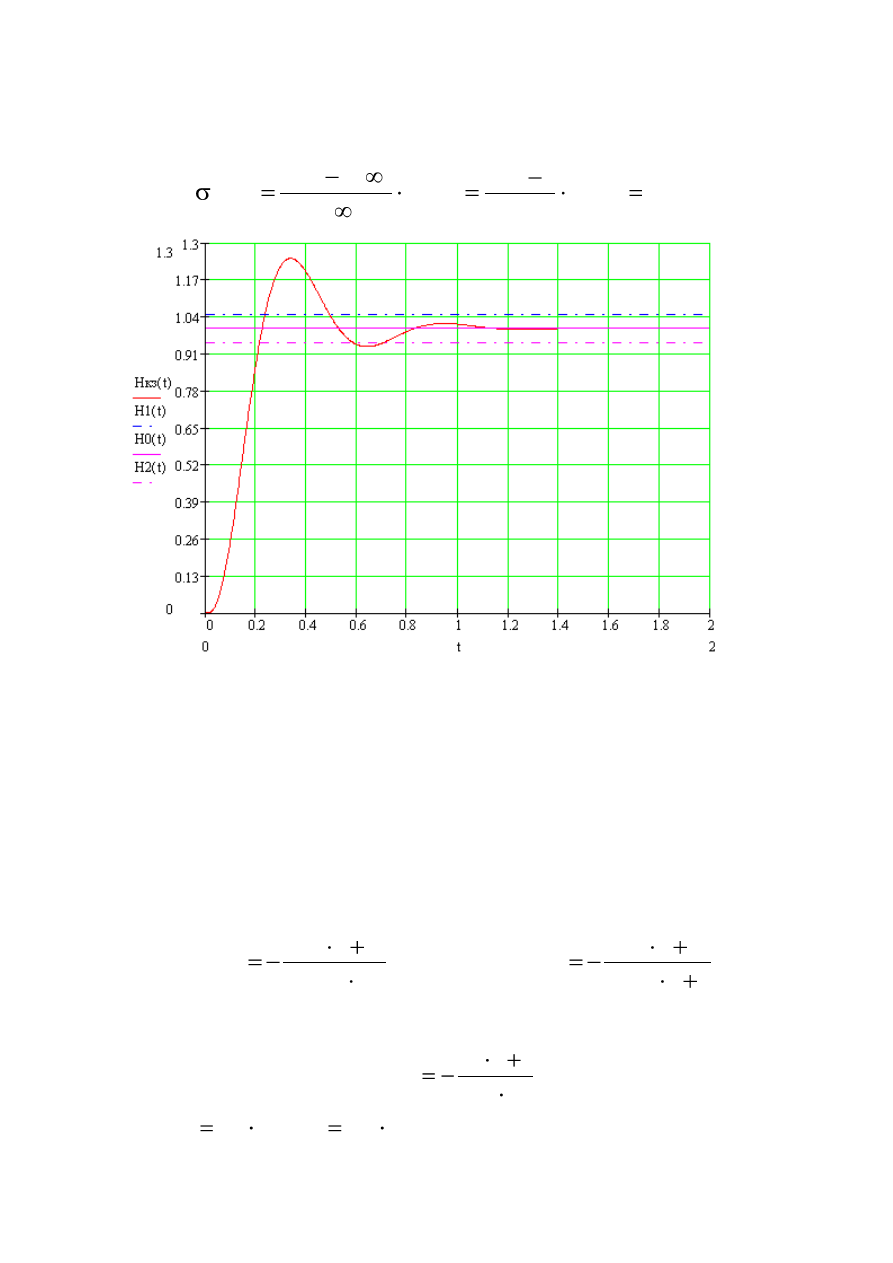
График переходного процесса представлен на рис. 27.
По графику переходного процесса можно определить показатели
качества:
47
время переходного процесса
t
p
=0,72c,
перерегулирование
%.
25
%
100
1
1
25
,
1
%
100
)
(
y
)
(
y
y
%
max
max
Рис.27. График переходного процесса
В результате получили систему, которая соответствует требуемым
показателям качества.
4.2.5. Синтез корректирующего звена из R, L, C элементов
По передаточной функции корректирующего звена произведем подбор
корректирующего устройства из R, L, C элементов по таблицам из [3].
Разобьем W
кз
(s) на два корректирующих устройства:
;
s
97
,
2
)
1
s
7
,
0
(
)
s
(
W
1
кз
.
1
s
667
,
1
1
s
7
,
0
)
s
(
W
2
кз
Передаточная функция W
кз1
(s) имеет вид:
;
s
T
1
s
T
)
s
(
W
1
2
1
кз
где
;
C
R
T
1
1
1
.
C
R
T
1
2
2