Добавлен: 21.10.2018
Просмотров: 3252
Скачиваний: 12
33
Так как
0
0
a
;
0
1
a
;
0
2
a
;
0
3
a
, а их соотношение
0
35
,
0
3
0
2
1
a
a
a
a
,
следовательно, заданная система, согласно критерию Гурвица, неустойчива.
Построим (рис.17) ЛАЧХ неизменяемой части системы:
)
1
9
,
0
)(
1
1
,
0
(
15
)
(
НЧ
s
s
s
s
W
.
Частоты сопряжения асимптотической ЛАЧХ
)
(
Н
L
:
1
-
1
1
1
,
1
9
,
0
1
1
c
T
,
1
-
2
2
10
1
,
0
1
1
c
T
.
Добротность системы по скорости при
1 равна:
дБ
23,5
lg15
20
3.2.1. Построение желаемой ЛАЧХ
Для заданного значения
%
30
max
по номограмме на рис. 8 [2]
определяем
27
,
1
max
P
. Тогда
cp
P
t
6
,
3
, откуда частота среза для желаемой
ЛАЧХ
1
min
3
,
7
5
,
1
6
,
3
6
,
3
c
t
P
СP
. Так как при наличии начального
рассогласования
рад
2
,
0
ускорение выходной координаты ограничивается
значением
2
с
рад
25
, то частота среза должна быть не более, чем:
1
Pmax
8
,
11
2
,
0
25
c
С
.
Следовательно, частоту среза для желаемой ЛАЧХ выбираем в диапазоне:
1
1
8
,
11
3
,
7
c
c
cp
Из соответствующих номограмм (рис. 9), которые позволяют определять
требования к желаемой ЛАЧХ разомкнутой системы в среднем диапазоне
частот, обеспечивающей получение переходной характеристики со значением
%
30
max
, находим избыток фазы
изб
и предельное значение
max
L
.
Тогда среднечастотная асимптота
)
(
L
проводится под наклоном
дБ/дек
20
, так как при больших наклонах трудно обеспечить устойчивость
системы и необходимое перерегулирование. Протяженность
)
(
L
под
наклоном
дБ/дек
20
устанавливаем, исходя из необходимого запаса
устойчивости по амплитуде
L
, т. е. не менее 11 дБ.
Низкочастотная асимптота
L
, определяющая статические свойства

34
системы, проходит через точку 23,5 дБ при
1
. Так как
)
1
9
,
0
)(
1
1
,
0
(
15
)
(
НЧ
s
s
s
s
W
имеет
k
и
порядок
астатизма
1
,
удовлетворяющие техническому заданию, то низкочастотная часть желаемой
ЛАЧХ соответствует низкочастотной части неизменяемой системы.
Среднечастотную и низкочастотную части сопрягаем под наклоном
дБ/дек
40
, т. е. таким образом, чтобы было наименьшее число изломов
асимптотической желаемой ЛАЧХ.
Высокочастотная часть не влияет ни на устойчивость, ни на качество,
поэтому ее проводим под таким же наклоном, как и у неизменяемой системы.
Необходимые построения представлены на рис. 17. Таким образом, получаем
желаемую ЛАЧХ, передаточная функция которой имеет вид:
2
)
1
024
,
0
)(
1
56
,
1
(
)
1
8
,
0
(
15
)
(
s
s
s
s
s
W
.
Далее определяем передаточную функцию замкнутой системы с
)
(s
W
и
проверяем её на устойчивость по критерию Гурвица. Характеристическое
уравнение замкнутой системы имеет вид:
0
15
91
,
12
61
,
1
10
48
,
7
10
83
,
8
)
1
8
,
0
(
15
)
1
024
,
0
)(
1
56
,
1
(
2
3
2
4
4
2
s
s
s
s
s
s
s
s
.
Тогда коэффициенты характеристического уравнения
4
0
10
83
,
8
a
;
2
1
10
48
,
7
a
;
61
,
1
2
a
;
91
,
12
3
a
,
15
4
a
.
Для устойчивости системы необходимо и достаточно, чтобы при
0
i
a
все
определители Гурвица были больше 0. При положительности всех
коэффициентов характеристического уравнения для устойчивости системы
требуется выполнение условия:
0
)
(
4
2
1
3
0
2
1
3
a
a
a
a
a
a
a
, или в числах
0
10
5
,
2
15
)
10
83
,
8
(
)
91
,
12
10
83
,
8
61
,
1
10
48
,
7
(
91
,
12
2
2
4
4
2
Следовательно, система устойчива.
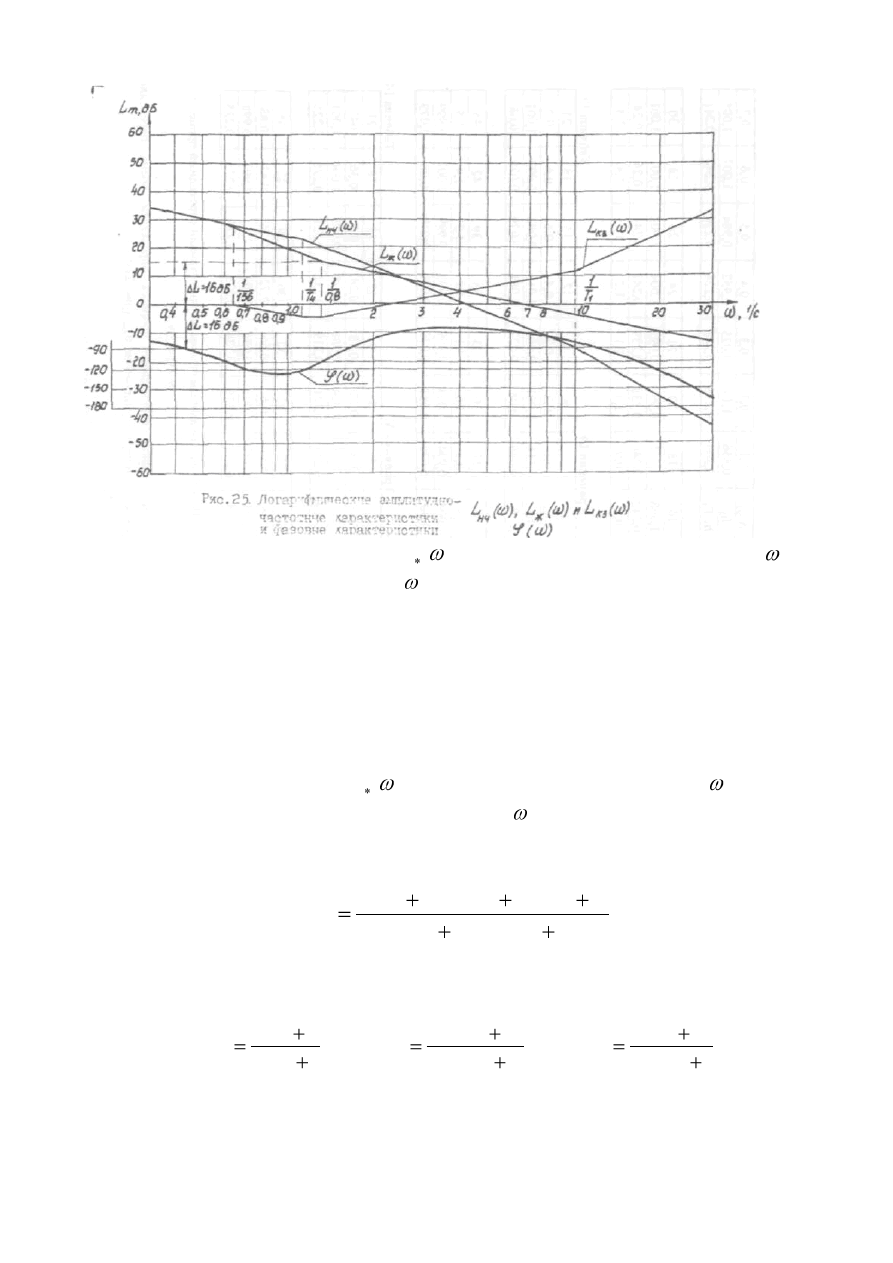
35
Рис. 17. Желаемая ЛАЧХ системы
)
(
L
, ЛАЧХ неизменяемой части
)
(
НЧ
L
и
ЛАЧХ корректирующего звена
)
(
КЗ
L
.
3.2.2. Синтез передаточной функции корректирующего звена
Произведем синтез последовательного корректирующего звена.
Несмотря на его сложную передаточную функцию - это наиболее простой
вариант синтеза.
Для получения ЛАЧХ корректирующего звена необходимо графически
вычесть из желаемой ЛАЧХ
)
(
L
ЛАЧХ неизменяемой части
)
(
НЧ
L
и далее
по точкам излома получаемой ЛАЧХ
)
(
КЗ
L
определить аналитическую
зависимость и постоянные времени передаточной функции
)
(
кз
s
W
. Проведя эти
операции, получаем:
2
кз
)
1
024
,
0
)(
1
54
,
1
(
)
1
1
,
0
)(
1
77
,
0
)(
1
9
,
0
(
)
(
s
s
s
s
s
s
W
.
Разобьем эту передаточную функцию на три части:
1
54
,
1
1
9
,
0
)
(
кз1
s
s
s
W
,
)
1
024
,
0
(
1
77
,
0
)
(
кз2
s
s
s
W
,
1
024
,
0
1
1
,
0
)
(
кз3
s
s
s
W
.
По этим передаточным функциям производится подбор корректирующего
звена из RLС - элементов по таблицам из [2] и расчет значений элементов.
36
3.2.3. Построение переходного процесса
Расчёт переходного процесса произведем методом трапеций. Для этого
определим вид вещественной характеристики замкнутой системы
)
(
P
.
Вещественную частотную характеристику получаем из номограммы,
представленной на рис.13. На номограмму наносим ЛАЧХ разомкнутой
скорректированной системы
)
(s
W
P
и получаем вещественную частотную
характеристику замкнутой системы
)
(
P
. Разобьем ее на пять трапеций. Для
каждой трапеции определяем значения
j
j
j
j
P
,
,
,
2
1
Процесс построения переходного процесса показан на рис. 18-19 и
представлен в табл. 6-10.
Таблица 6
N
j
1
j
2
j
j
P
I
0,5
0,9
0,55
-0,03
П
1,6
11,3
0,138
0,92
III
11,3
20
0,565
0,24
IV
20
30
0,666
0,08
V
42
50
0,7
-0,21
Задавшись величиной шага таблицы
h
функций, получаем шаг
построения переходного процесса в реальном времени для каждой j-ой
трапеции:
c
t
t
p
22
,
0
9
,
0
2
,
0
21
1
1
,
c
t
t
p
084
,
0
3
,
11
1
22
2
2
,
c
t
t
p
1
,
0
20
2
23
3
3
,
c
t
t
p
1
,
0
30
3
24
4
4
,
c
t
t
p
6
,
0
50
30
25
5
5
.
Используя таблицы
h
функций [2], заполняем таблицы 7-11 для
построения переходных процессов.
Таблица 7. Трапеция I
1
t
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1
p
t
0,22
0,44
0,66
0,88
1,0
1,32
1,54
1
h
0,098
0,196
0,292
0,386
0,476
0,562
0,662
1
1
P
h
0,003
0,006
0,009
0,012
0,014
0,017
0,02

37
Таблица 8. Трапеция II
2
t
1
2
3
4
5
6
7
2
p
t
0,088
0,176
0,265
0,354
0,442
0,530
0,618
2
h
0,34
0,655
0,862
0,973
1,012
1,012
1,006
2
2
P
h
0,313
0,602
0,793
0,931
0,931
0,932
0,925
9
10
11
12
13
14
15
16
0,795
0,884
0,972
1,061
1,145
1,223
1,332
1,146
1,016
1,025
1,028
1,025
1,019
1,015
1,014
1,014
0,934
0,943
0,946
0,943
0,937
0,933
0,936
1,014
Таблица 9. Трапеция III
3
t
2
4
6
8
10
12
14
3
p
t
0,1
0,2
0,3
0,4
0,5
0,6
0,7
3
h
0,856
1,15
1,035
0,952
0,984
1,007
1,005
3
3
P
h
0,205
0,276
0,248
0,228
0,236
0,242
0,241
16
18
20
22
24
26
28
30
1,008
1,001
0,991
0,997
1,004
1,002
1,001
1,001
0,242
0,240
0,238
0,239
0,241
0,241
0,24
0,24
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
Таблица 10. Трапеция IV
4
t
3
6
9
12
15
18
21
4
p
t
0,1
0,2
0,3
0,4
0,5
0,6
0,7
4
h
1,116
1,001
0,966
1,011
0,992
0,993
1,001
4
4
P
h
0,084
0,08
0,077
0,081
0,079
0,079
0,08
24
27
30
33
36
39
42
45
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,004
0,994
1,003
0,999
0,993
0,999
1,002
0,999
0,08
0,079
0,083
0,079
0,079
0,079
0,08
0,079
Таблица 11. Трапеция V
5
t
3
6
9
12
15
18
21
5
p
t
0,06
0,12
0,18
0,24
0,3
0,36
0,42
5
h
1,13
0,984
0,986
1,028
0,983
1,004
1,001
5
5
P
h
0,254
0,221
0,219
0,231
0,221
0,226
0,225