Добавлен: 21.10.2018
Просмотров: 3256
Скачиваний: 12
38
24
27
30
33
36
39
42
45
0,48
0,54
0,6
0,66
0,72
0,76
0,82
0,88
0,991
0,997
1,005
0,996
1,002
1,0
0,997
0,998
0,225
0,224
0,225
0,224
0,225
0,225
0,225
0,225
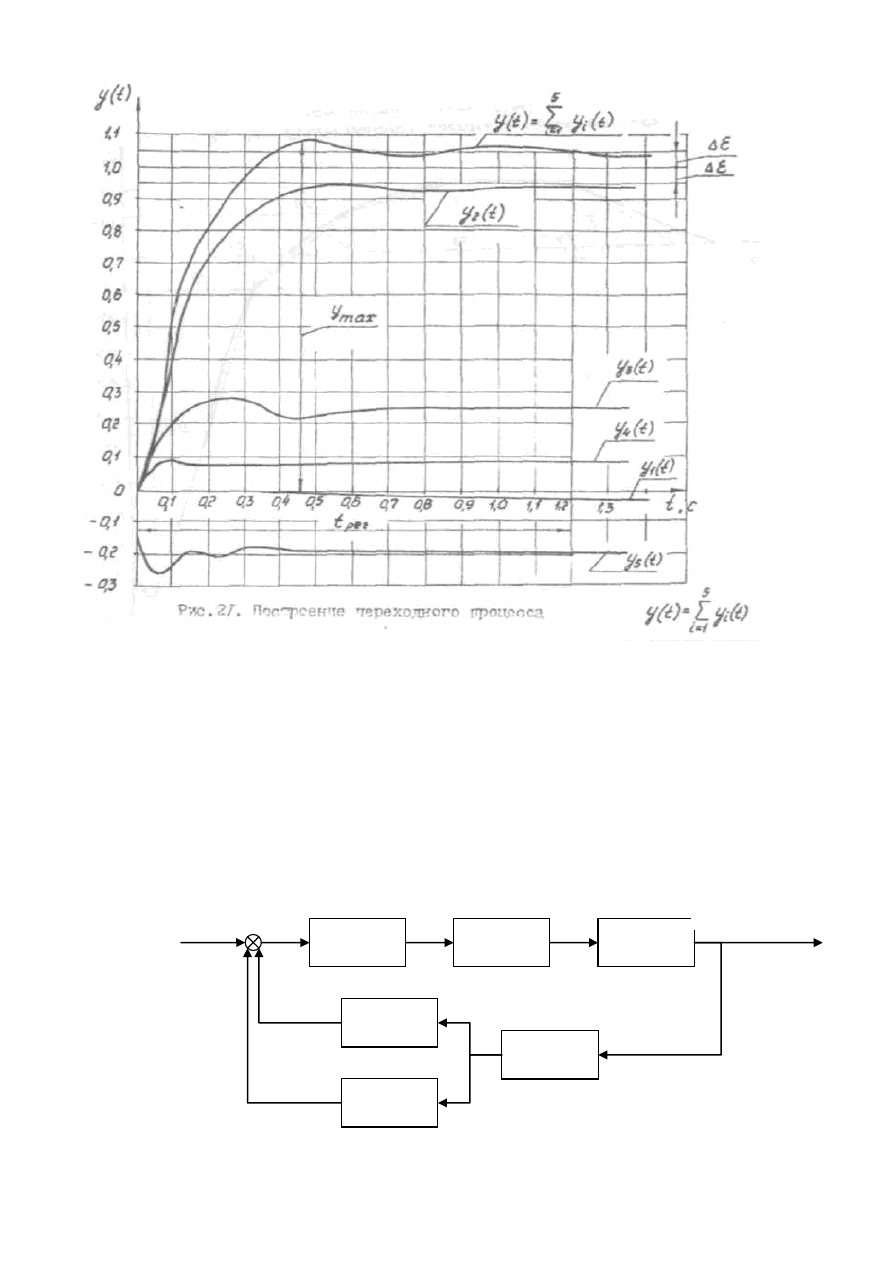
По табличным данным строим результирующий переходный процесс:
5
1
)
(
)
(
i
i
t
y
t
y
.
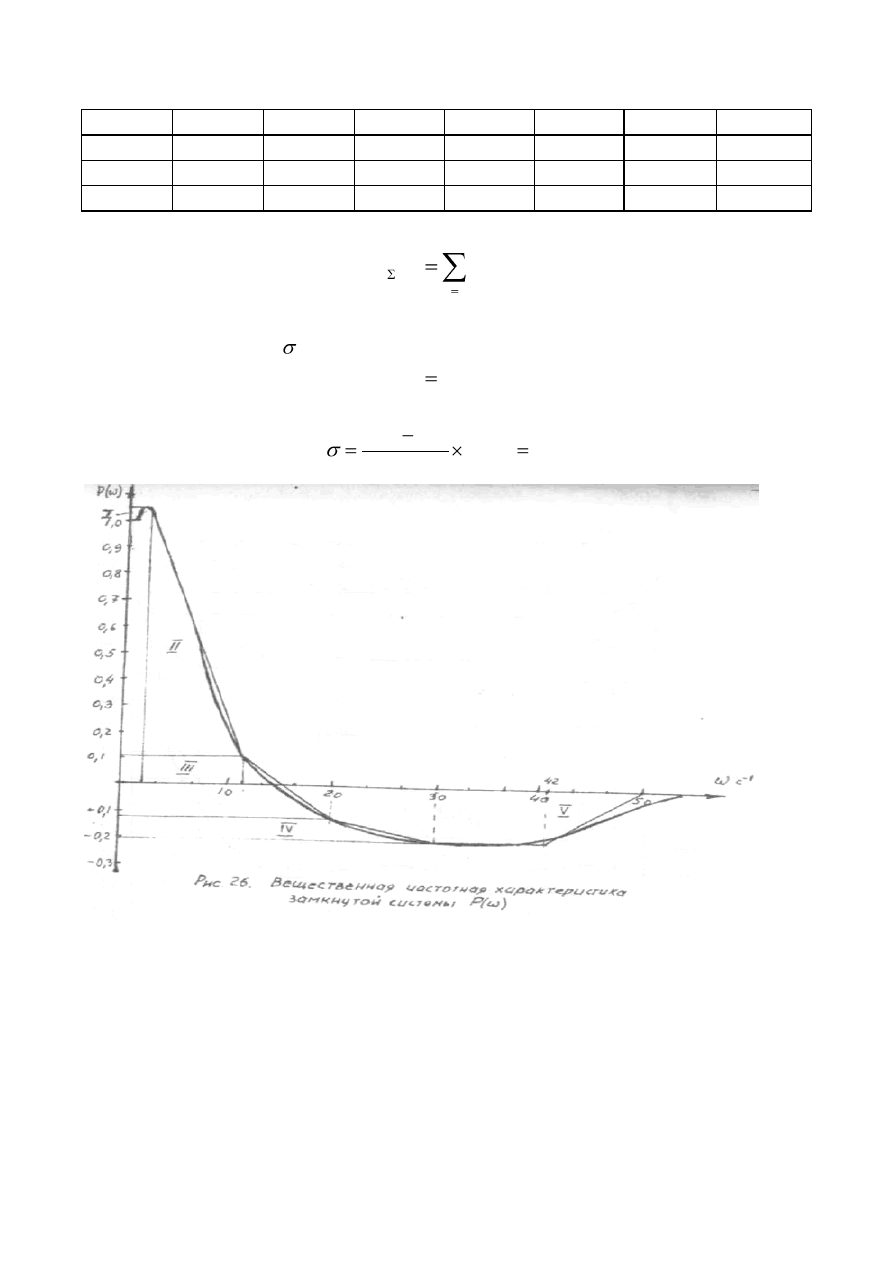
По графику переходного процесса определяем время переходного процесса
p
t
и перерегулирование
max
(рис. 19):
c
t
p
2
,
1
,
%
5
%
100
уст
уст
max
y
y
y
.
Рис 18. Вещественная частотная характеристика замкнутой системы P(ω)
39
Рис 19. Построение переходного процесса
4. ПРИМЕР РАСЧЕТА ЗАДАНИЯ ПО КУРСОВОЙ РАБОТЕ
С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ Mathcad
4.1. Задание на курсовую работу
Задана структурная схема автоматической системы управления ЛА в
режиме стабилизации и управления углом тангажа (рис.20).
W
1
(s)
W
кз
(s)
υ
зад
(-)
Рис. 20 . Структурная схема системы «ЛА-САУ»
∆ε
W
2
(s)
W
4
(s)
W
3
(s)
W
5
(s)
(-)
ύ
υ
δ
в

40
Передаточные функции блоков системы :
;
1
s
T
k
)
s
(
W
1
1
1
;
1
s
T
2
s
T
k
)
s
(
W
4
2
2
4
3
3
;
1
s
T
k
)
s
(
W
2
2
2
;
k
)
s
(
W
4
.
s
k
)
s
(
W
'
5
Определить передаточную функцию корректирующего звена так, чтобы
система «ЛА-САУ» обладала следующими свойствами и показателями
качества:
астатизмом 1-го порядка;
передаточным коэффициентом разомкнутой системы k=10 c
-1
;
перерегулированием σ
max
%≤30 %;
временем переходного процесса t
р
≤2,5 c.
Максимальное ускорение регулируемой величины должно быть не более
10
рад
/
с
2
при начальном рассогласовании ∆ε=0,1 рад.
Построить переходной процесс скорректированной системы и показать,
что система «ЛА-САУ» удовлетворяет заданным требованиям.
Значения параметров системы :
k
1
=45; k
υ
=3; T
1
=0,06 c; k
2
=1,1; k
υ'
=5; T
2
=0,04 c;
k
3
=0,2; ξ=0,6; T
4
=0,7c.
На основе полученного вида передаточной функции корректирующего
звена синтезировать корректирующее звено из R, L, C элементов.
4.2. Типовой расчет по курсовой работе с использованием
системы Mathcad
4.2.1. Построение ЛАЧХ неизменяемой части системы
Преобразуем исходную структурную схему нескорректированной САУ к
виду, представленному на рис. 21, где
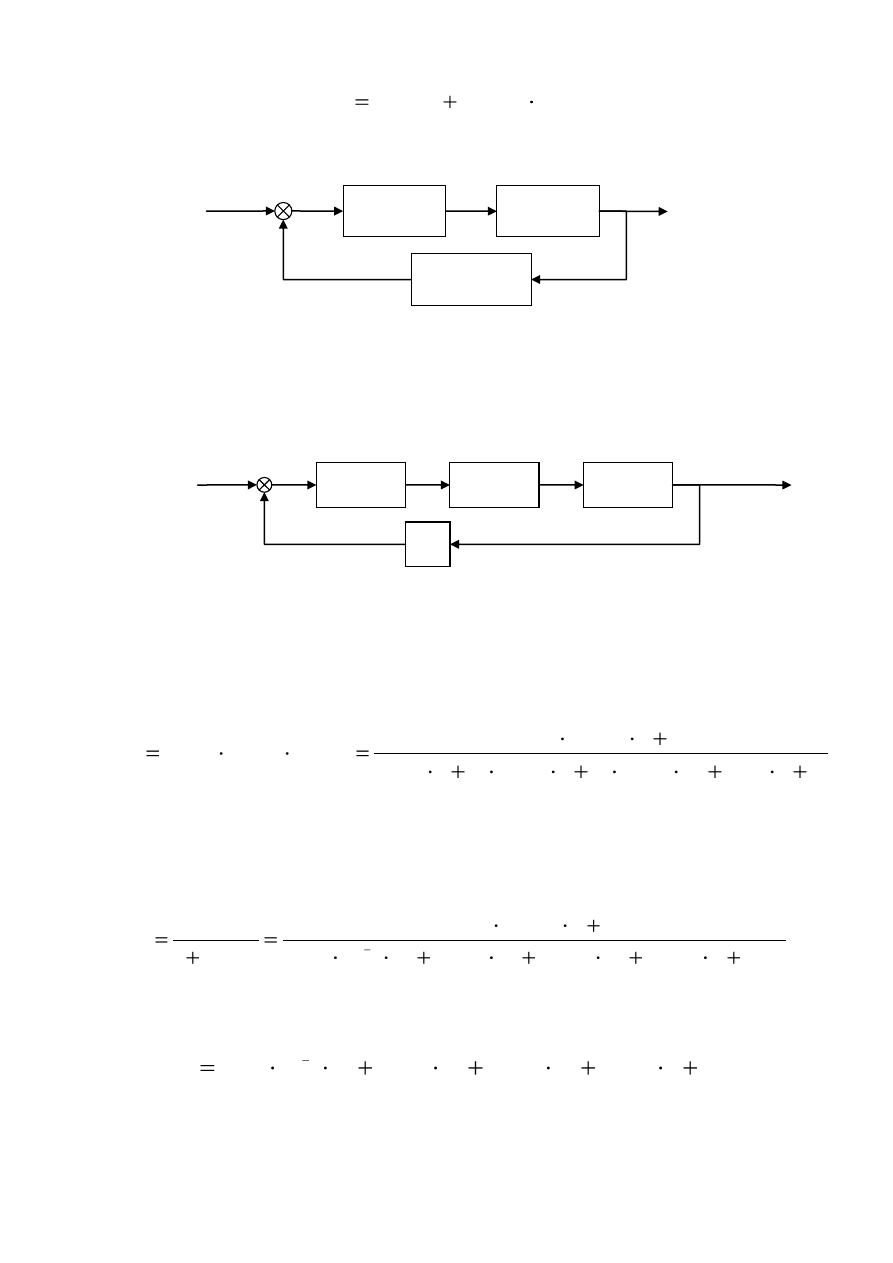
41
).
s
(
W
))
s
(
W
)
s
(
W
(
)
s
(
W
3
5
4
ос
В результате дальнейших преобразований получаем структурную схему с
единичной обратной связью (рис. 22).
Передаточная функция разомкнутой нескорректированной системы имеет
вид:
.
)
1
84
,
0
49
,
0
(
)
1
04
,
0
(
)
1
06
,
0
(
)
1
667
,
1
(
7
,
29
)
(
)
(
)
(
)
(
2
2
1
s
s
s
s
s
s
W
s
W
s
W
s
W
ос
р
Определим устойчивость заданной системы в замкнутом состоянии. Для
этого следует найти характеристическое уравнение замкнутой системы.
Передаточная функция замкнутой нескорректированной системы:
.
7
,
29
44
,
50
576
,
0
051
,
0
10
176
,
1
)
1
667
,
1
(
7
,
29
)
(
1
)
(
)
(
2
3
4
3
s
s
s
s
s
s
W
s
W
s
W
р
р
з
Тогда характеристическое уравнение замкнутой системы:
7
.
29
44
.
50
576
.
0
051
.
0
10
176
,
1
)
(
2
3
4
3
s
s
s
s
s
D
Коэффициенты характеристического уравнения равны:
a
0
=1,176∙10
-3
; a
2
=0,576; a
4
=29,7; a
1
=0,051; a
3
=50,44.
W
1
(s)
W
2
(s)
-1
υ
зад
(-)
Рис.22. Структурная схема САУ с единичной обратной
связью
∆ε
W
ос
(s)
W
1
(s)
W
2
(s)
W
ос
(s)
δ
в
υ
зад
(-)
Рис.21. Преобразованная структурная схема САУ
∆ε
42
Для устойчивости системы необходимо и достаточно, чтобы при
положительности всех коэффициентов характеристического уравнения (a
i
>0)
все определители Гурвица были больше нуля.
Т.к. а
0
>0, а
1
>0, а
2
>0, а
3
>0, а
4
>0, то для устойчивости системы требуется
выполнение условия:
3
0
2
1
2
а
а
а
а
0
03
,
0
2
4
2
1
2
3
0
3
2
1
3
а
а
а
а
а
а
а
0
586
,
1
3
Следовательно, нескорректированная система не устойчива.
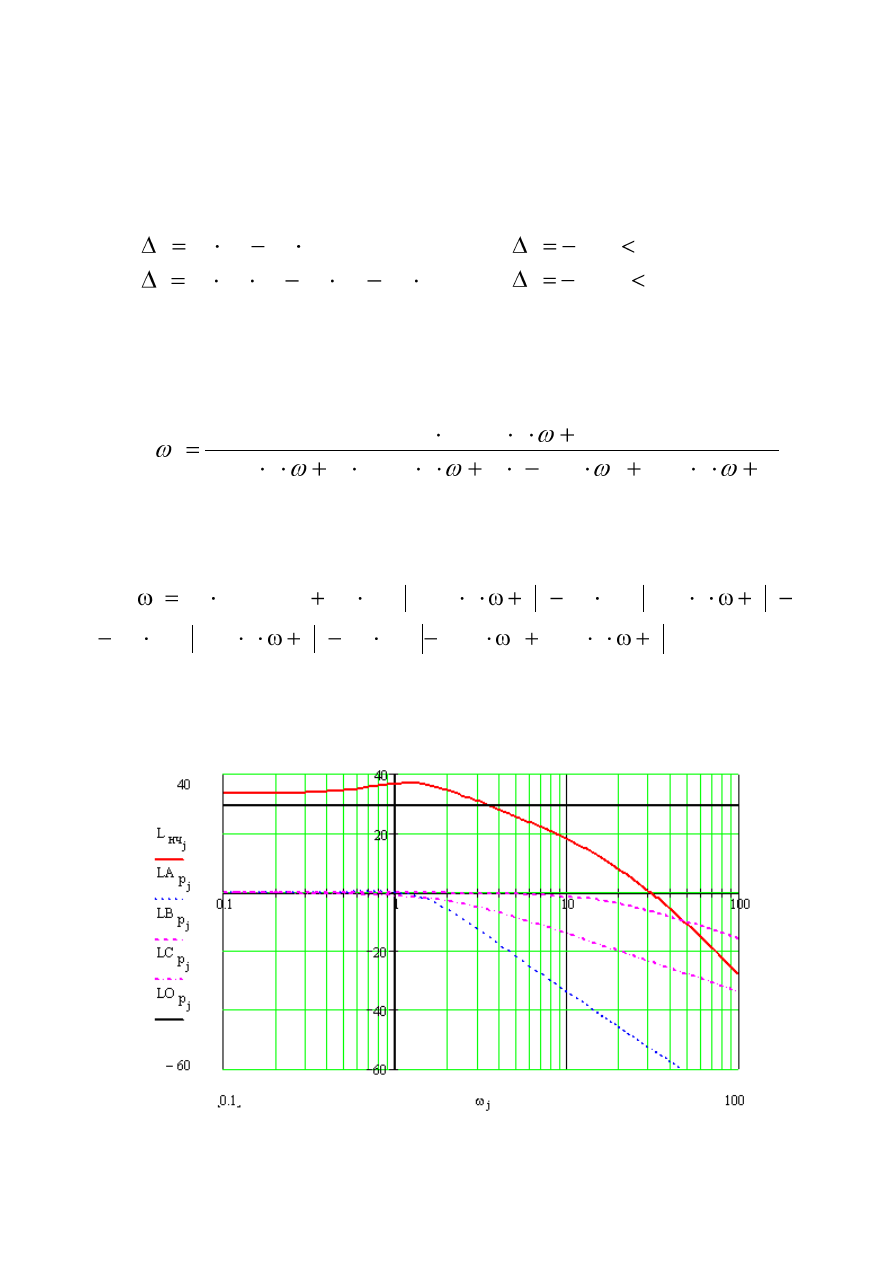
Построим ЛАЧХ неизменяемой части системы по следующей
передаточной функции:
.
)
1
84
,
0
49
,
0
(
)
1
04
,
0
(
)
1
06
,
0
(
)
1
667
,
1
(
7
,
29
)
(
2
i
i
i
i
i
W
нч
Для этого представим ЛАЧХ неизменяемой части системы как сумму
ЛАЧХ типовых звеньев, т.е.
).
1
i
84
,
0
49
,
0
log(
20
)
1
i
04
,
0
log(
20
)
1
i
06
,
0
log(
20
)
1
i
667
,
1
log(
20
)
7
,
29
log(
20
)
(
L
2
нч
Система является неустойчивой, но как видно из ЛАЧХ (рис. 23) система
не имеет необходимого требуемого запаса по фазе и амплитуде.
Рис.23. ЛАЧХ неизменяемой части системы