Файл: МР_Курс.Раб. Теория систем и системный анализ. ЗЭИ_2017_сп.pdf

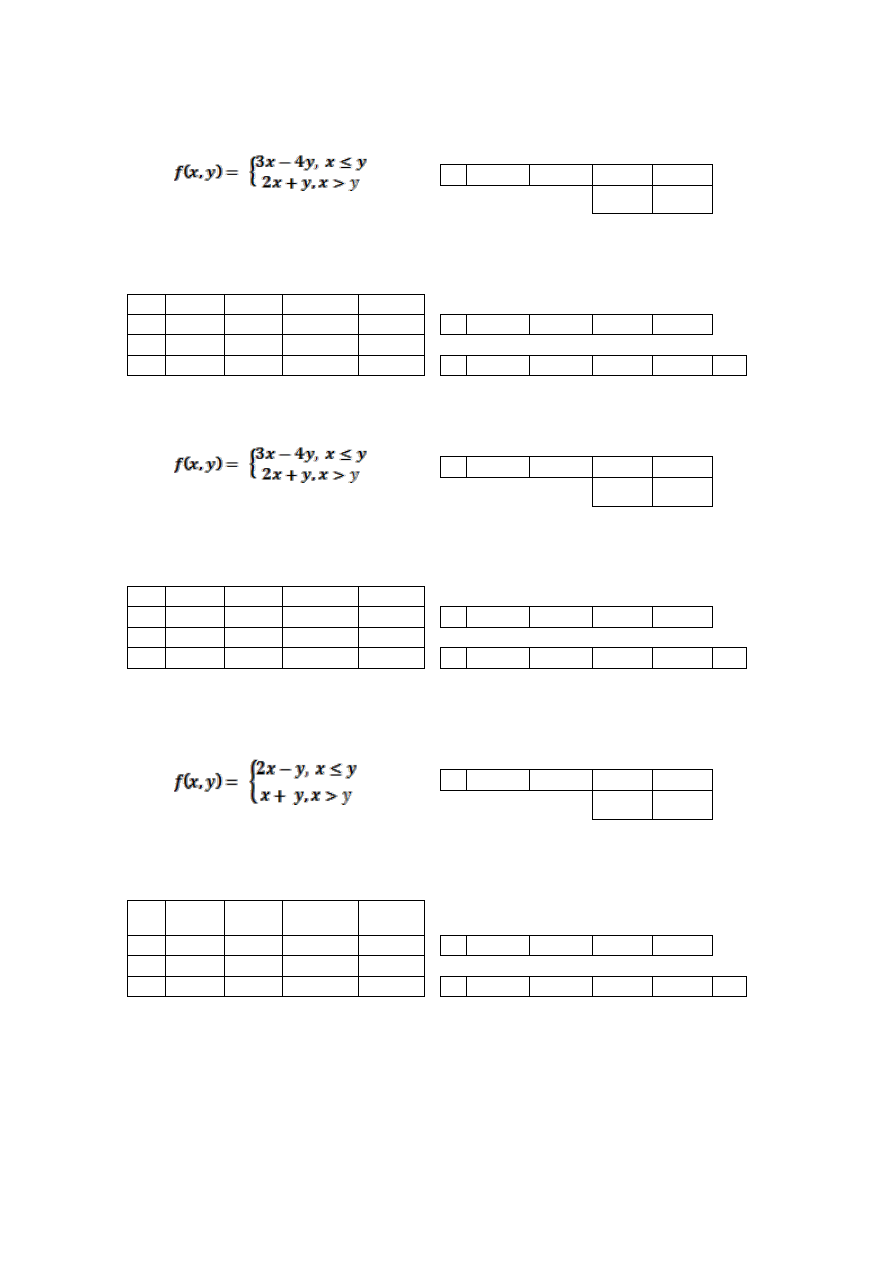
31 

48.   

`Платежная функция 

Значения вероятностей состояний 
внешней среды 

  P 

0,10 

0,58 

0,20 

0,12 

xЄX, 

yЄY 

  Параметр Гурвица 

λ = 

0,84 

Матрица условных вероятностей со-
стояний неидеального эксперимента 
при фиксированных состояниях внеш-
ней среды 

П1 

П2 

П3 

П4 

  Значения состояний внешней среды 

В1 

0,81 

0,09 

0,11 

0,12 

  Y 

9 

10 

11 

12 

В2 

0,12 

0,56 

0,17 

0,23 

  Значения стратегий 

В3 

0,07 

0,35 

0,72 

0,65 

  X 

7 

8 

9 

9,5 

13 

49.   

`Платежная функция 

Значения вероятностей состояний 
внешней среды 

  P 

0,09 

0,59 

0,20 

0,12 

xЄX, 

yЄY 

  Параметр Гурвица 

λ = 

0,54 

Матрица условных вероятностей со-
стояний неидеального эксперимента 
при фиксированных состояниях внеш-
ней среды 

П1 

П2 

П3 

П4 

  Значения состояний внешней среды 

В1 

0,77 

0,11 

0,13 

0,14 

  Y 

9 

10 

11 

12 

В2 

0,12 

0,54 

0,19 

0,25 

  Значения стратегий 

В3 

0,11 

0,35 

0,68 

0,61 

  X 

7 

9 

11 

12 

13 

 
50.  

 Платежная функция 

Значения вероятностей состояний 
внешней среды 

  P 

0,25 

0,10 

0,14 

0,51 

xЄX, 

yЄY 

  Параметр Гурвица 

λ = 

0,35 

Матрица условных вероятностей со-
стояний неидеального эксперимента 
при фиксированных состояниях внеш-
ней среды 

П1 

П2 

П3 

П4 

Значения состояний внешней сре-
ды 

В1 

0,80 

0,14 

0,15 

0,12 

  Y 

8 

9 

10 

11 

В2 

0,12 

0,55 

0,45 

0,35 

  Значения стратегий 

В3 

0,08 

0,31 

0,40 

0,53 

  X 

7 

8 

9 

10 

11 

Задание № 3 
 

32 

1. 

Разработка  управленческого  решения  при  планировании  развития  лечебного 
учреждения

Администрация больницы в г. Почаеве решает, следует ли сделать к больнице большую 

пристройку,  маленькую  пристройку  или  не  делать  пристройки  вообще.  Если  население  Почаева 
будет  продолжать  расти,  то  большая  пристройка  могла  бы  приносить  ежемесячно  дополнитель-
ную прибыль в 1500 тыс. руб. Если будет сделана маленькая пристройка, то она может приносить 
больнице  600  тыс.  руб.  прибыли  ежемесячно  при  условии,  что  население  будет  увеличиваться. 
Если  население  Почаева  уменьшится,  то  сооружение  большой  пристройки  принесет  больнице 
убыток в 850 тыс. руб., а маленькой — в 450 тыс. руб. Если же население Почаева не будет ме-
няться, то сооружение большой пристройки принесет больнице прибыль в 600 тыс. руб., а малень-
кой — в 400 тыс. руб. К сожалению, у администрации больницы нет информации о том, как будет 
меняться численность населения Почаева. 

Итак,  у  администрации  больницы  в  г.  Почаеве  имеются  следующие  альтернативы:  по-

строить большую пристройку или маленькую или ничего не делать вообще. 

1.1.  

Постройте таблицу решений (платежную матрицу). Определите наилучшие альтер-

нативы для администрации больницы в г. Почаеве, используя критерии максимина, ми-
нимаксного риска и недостаточных оснований. 

Чему равны значения оптимальных выигрышей для наилучших альтернатив по ка-

ждому из используемых критериев? Какие альтернативы являются наилучшими по каж-
дому из критериев? 

1.2.  

Определите  наилучшее  решение,  используя  критерий  максимизации  ожидаемой 

прибыли,  в  том  случае,  если  бы  у  администрации  больницы  имелась  дополнительная 
информация о вероятностях изменения численности населения г. Почаева. Вероятность 
того, что падения численности населения не случится, равна 0,6, а вероятность того, что 
его численность останется неизменной, равна 0,35.  

Чему равно значение ожидаемой прибыли больницы для наилучшей альтернативы 

при наличии такой дополнительной информации? Какова оптимальная стратегия?  

Чему  равно  значение  оптимального  среднего  выигрыша  в  случае  проведения  иде-

ального эксперимента? Определите цену достоверной информации при проведении иде-
ального  эксперимента.  Объясните, какие  наилучшие  стратегии  следует  выбирать лицу, 
принимающему  решение,  при  известных  результатах  идеального  эксперимента?  Дайте 
свою  неформальную  интерпретацию  понятию  «идеальный  эксперимент»  для  рассмат-
риваемой ситуации.  

Проведите сравнение полученных результатов со случаем, для которого вместо пре-

дыдущего  выполняется  следующее  условие:  вероятность  того,  что  роста  численности 
населения не произойдет, равна 0,6, а вероятность того, что его численность останется 
неизменной, равна 0,35.   

1.3.  

Предположим,  что  администрация  больницы  может  воспользоваться  услугами  де-

мографического бюро по  уточнению  прогноза изменения численности г. Почаева. Дан-
ные по адекватности оценки прогноза демографическим бюро приведены в таблице: 

1.4.  

Прогноз

Реальная ситуация

Рост численности

Неизменная числен-

ность

Падение численности

Рост численности

75%

20%

10%

Неизменная численность

20%

65%

30%

Падение численности

5%

15%

60%

33 

 
Какова  величина  максимальной  денежной  суммы,  которую  администрация  больницы 
согласилась бы заплатить за прогноз демографического бюро? Изменится ли эта вели-
чина (и на сколько?), если вероятности изменения численности населения г. Почаева бу-
дут следующими: вероятность падения численности населения равна 0,3, а вероятность 
того,  что  численность  населения  останется  неизменной,  равна  0,1?  Объясните,  какие 
наилучшие стратегии следует выбирать лицу, принимающему решение, при известных 
результатах неидеального эксперимента? Постройте таблицу, из которой было бы видно, 
какую стратегию надо выбирать при том или ином исходе неидеального эксперимента. 
Сравните результаты такого выбора для трех наборов вероятностей реализации состоя-
ний внешней среды.  

1.4.  

Проанализируйте,  насколько  существенно  изменится  решение,  если  вероятности 

изменения  численности  населения  г.  Почаева  известны  неточно.  Исследуйте  устойчи-
вость решения при варьировании в максимально возможном диапазоне соотношения ве-
роятностей следующих состояний внешней среды: “численность населения увеличива-
ется”,  “численность  населения  уменьшается”  (считая  значение  вероятности  состояния 
“численность населения остается прежней” неизменной). Расчеты проведите для набора 
вероятностей  реализации  состояний  внешней  среды,  который  приведен  в  п.  1.2.  По-
стройте графики зависимостей оптимальной величины выигрыша и цен совершенной и 
несовершенной информации от величины вероятности состояния “численность населе-
ния увеличивается” и определите, при каких значениях варьируемого параметра проис-
ходят изменения в выборе оптимальной стратегии. 

1.5.  

Проанализируйте, насколько существенно изменится решение, если значение до-

полнительной прибыли администрации от введения в эксплуатацию большой пристрой-
ки при росте численности населения г. Почаева известно неточно, но анализ показывает, 
что это значение должно лежать в пределах от 1200 до 1800 тыс. руб. Исследуйте ус-
тойчивость решения, и определите зависимости основных выходных данных задачи 
(оптимальные стратегии и величины выигрышей по всем применяемым критериям, це-
ны совершенной и несовершенной информации) от величины дополнительной прибыли 
администрации от введения в эксплуатацию большой пристройки при росте численно-
сти населения при ее варьировании в заданных пределах. По критерию Байеса расчеты 
проведите для набора вероятностей реализации состояний внешней среды, который 
приведен в п. 1.3. Постройте графики зависимостей оптимальных величин выигрышей, 
цены совершенной информации и цены несовершенной информации от величины этой 
прибыли и определите, при каких значениях варьируемого параметра происходят изме-
нения в выборе оптимальных стратегий. 
 

2. 

Разработка  управленческого  решения  при  планировании  развития  предпри-
ятия розничной торговли

Предприниматель 

предполагает 

построить 

ресторан 

недалеко 

от 

торгово-

развлекательного центра. Один из возможных вариантов – предусмотреть в нем открытие пивного 
бара.  Другой  вариант  не  связан  с  продажей  пива.  В  обоих  случаях  предприниматель  оценивает 
свои шансы на успех как 0,6 (благоприятный рынок) и на неудачу - как 0,4 (неблагоприятный ры-
нок). Предварительные обсуждения показывают, что при благоприятном рынке план, связанный с 
продажей пива, может принести 3250 тыс. руб. прибыли, без продажи пива можно заработать 2500 
тыс. руб. прибыли. При неблагоприятном рынке убытки в случае открытия ресторана с баром со-
ставят 800 тыс. руб., в случае ресторана без бара — 200 тыс. руб. 

2.1.  

Выберите наилучшую альтернативу для предпринимателя на основе максимальной 

средней стоимостной оценки в качестве критерия. Следует ли реализовать план, преду-

34 

сматривающий продажу пива? Предварительно постройте таблицу решений (платежную 
матрицу).

2.2.  

Определите наилучшее решение. Чему равно значение среднего выигрыша для наи-

лучшей альтернативы? 

2.3.  

Определите  наилучшее  решение,  используя  критерий  максимизации  ожидаемой 

прибыли, в том случае, если бы шансы на успех были оценены предпринимателем как 
0,4  (благоприятный  рынок),  а  шансы  на  неудачу  –  как  0,6  (неблагоприятный  рынок). 
Рассчитайте также и величину оптимального выигрыша. Проведите сравнение результа-
та с предыдущим вариантом оценки шансов на реализацию благоприятного и неблаго-
приятного рынка. 

Определите  цену  достоверной  информации  при  проведении  идеального  экспери-

мента. Объясните, какие наилучшие стратегии следует выбирать лицу, принимающему 
решение, при известных результатах идеального эксперимента?  

Постройте таблицу, из которой было бы видно, какую стратегию надо выбирать при 

том  или  ином  исходе  идеального  эксперимента.  Проведите  сравнение  полученных  ре-
зультатов для двух наборов упомянутых выше вероятностей реализации благоприятного 
или  неблагоприятного  рынка.  Дайте  свою  неформальную  интерпретацию  понятию 
«идеальный эксперимент» для рассматриваемой ситуации. 

2.4.  

Предположим,  что  предприниматель  может  воспользоваться  услугами  центра  ис-

следования  рыночной  конъюнктуры  по  уточнению  прогноза  относительно  реализации 
благоприятного или неблагоприятного рынка. Данные по адекватности оценки прогноза 
центром исследования рыночной конъюнктуры приведены в таблице: 

a.   

Прогноз 

Реальная ситуация

Благоприятный рынок

Неблагоприятный рынок

Благоприятный рынок

75%

35%

Неблагоприятный рынок

25%

65%

 
Какова величина максимальной денежной суммы, которую предприниматель согласился 
бы заплатить за прогноз центра исследования рыночной конъюнктуры, если шансы на 
успех им оценены как 0,6 (благоприятный рынок) и на неудачу - как 0,4 (неблагоприят-
ный рынок)? Изменится ли эта величина (и на сколько?), если вероятности реализации 
благоприятного и неблагоприятного рынка были оценены предпринимателем как 0,4 и 
0,6  соответственно?  Приведите  также  списки  оптимальных  стратегий для обоих  набо-
ров  вероятностей  состояний  внешней  среды,  которые  следует  выбирать  лицу,  прини-
мающему решение, при известных результатах неидеального эксперимента. 

2.5.  

Чему равно значение прибыли предпринимателя для наилучшей альтернативы при 

отсутствии информации о шансах на реализацию благоприятного или неблагоприятного 
рынка?  Воспользуйтесь  критериями  максимакса,  минимаксного  риска  и  пессимизма-
оптимизма при значении параметра Гурвица, равного 0,3. Определите также и наилуч-
шие альтернативы для каждого из используемых критериев. 

2.6.  

Проанализируйте,  насколько  существенно  изменится  решение,  если  вероятности 

реализации  благоприятного  и  неблагоприятного  рынка  известны  неточно.  Исследуйте 
устойчивость решения при варьировании в диапазоне от 0 до 0,8 вероятности реализа-
ции  благоприятного  рынка.  Постройте  графики  зависимостей  оптимальной  величины 
выигрыша и цен совершенной и несовершенной информации от величины вероятности 

35 

реализации благоприятного рынка и определите, при каких значениях варьируемого па-
раметра происходят изменения в выборе оптимальной стратегии. 

2.7.  

Проанализируйте, насколько существенно изменится решение, если значение при-

были предпринимателя в случае постройки ресторана с пивным баром при благоприят-
ном рынке известно неточно, но анализ показывает, что это значение должно лежать в 
пределах от 2800 до 3400 тыс. руб. Исследуйте устойчивость решения и определите за-
висимости основных выходных данных задачи (оптимальные стратегии и величины вы-
игрышей по всем применяемым критериям, цену совершенной информации и цену не-
совершенной информации) от величины этой прибыли при ее варьировании в заданных 
пределах. По критерию Байеса расчеты проведите для набора вероятностей, приведен-
ных в начале задачи. Постройте графики зависимостей оптимальных величин выигры-
шей, цены совершенной информации и цены несовершенной информации от величины 
варьируемого параметра и определите, при каких значениях этого параметра происходят 
изменения в выборе оптимальных стратегий. 

3. 

Разработка  управленческого  решения  при  планировании  объемов  продажи 
химических реактивов

«Псиколор» – магазин, входящий в производственно-торговый холдинг и торгующий хи-

мическими  реактивами,  которые  используются  швейными  фабриками  для  окраски  тканей.  Один 
из  продуктов,  который  предлагает  «Псиколор»,  –  АВС-6.  Адам  Полутонов,  директор  магазина, 
продает в течение месяца 11, 12 или 13 ящиков реактива АВС-6. От продажи каждого ящика фир-
ма получает 35 тыс. руб. прибыли. Химреактив АВС-6, как и многие другие реактивы, имеет ма-
лый срок годности. Поэтому, если ящик не продан к концу месяца, Адам Полутонов отдает распо-
ряжение об его уничтожении. Так как каждый ящик обходится магазину в 56 тыс. руб., он теряет 
их в случае, если ящик не продан к концу месяца. Вероятности продать 11, 12 или 13 ящиков в те-
чение месяца равны соответственно 0,44, 0,36 и 0,20. 

3.1.  

Сколько ящиков с химическим реактивом АВС-6 следует закупать фирме для про-

дажи ежемесячно? Предварительно постройте таблицу решений (платежную матрицу). 

3.2.  

Какова ожидаемая стоимостная оценка оптимального решения? 

3.3.  

Сколько ящиков с реактивом АВС-6 следовало бы закупать для продажи, если Адам 

Полутонов смог бы на тех же условиях использовать этот химреактив с добавкой, кото-
рая значительно продлевает срок его годности, причем добавка является побочным про-
дуктом  химического  производства  одного  из  предприятий  холдинга,  в  который  входит 
магазин «Псиколор»? Как изменится оптимальное решение, если добавка производится 
на стороннем предприятии, и ее стоимость составляет 15 тыс. руб. на ящик?  

3.4.  

Определите  наилучшее  решение,  используя  критерий  максимизации  ожидаемой 

прибыли в том случае, если бы вероятности продать 11, 12 или 13 ящиков химреактивов 
в течение месяца были равны соответственно 0,20, 0,35 и 0,45. Рассчитайте также и ве-
личину оптимального выигрыша. Проведите сравнение результатов для данного и пре-
дыдущего вариантов оценки вероятностей.  

Чему  равно  значение  оптимального  среднего  выигрыша  в  случае  проведения  иде-

ального эксперимента для каждого из вариантов? Определите цену достоверной инфор-
мации при проведении идеального эксперимента. Объясните, какие наилучшие страте-
гии  следует  выбирать  лицу,  принимающему  решение,  при  известных  результатах  иде-
ального  эксперимента.  Изменятся  ли  эти  стратегии  при  изменении  вероятностей  со-
стояний внешней среды (сравните результаты для наборов вероятностей продать 11, 12