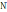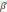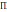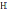Файл: Контрольные работы. Теория автоматического управления.docx
ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Методичка
Дисциплина: Теория автоматического управления
Добавлен: 19.10.2018
Просмотров: 5338
Скачиваний: 88
5. Настройка параметров регуляторов систем с апериодической реакцией.
Довольно
часто от системы управления требуется,
чтобы её переходная характеристика как
можно быстрее стремилась к установившемуся
значению с минимальным перерегулированием.
Системы такого типа принято называть
системами
с апериодической реакцией.
В качестве меры близости переходной
характеристики к установившемуся
значению принимают зону, равную 2% от
этого значения. Тогда временем установления
считают время
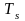 ,
за которое переходная характеристика
входит в указанную зону, как показано
на рис. 1. Апериодическая реакция
характеризуется следующими показателями:
,
за которое переходная характеристика
входит в указанную зону, как показано
на рис. 1. Апериодическая реакция
характеризуется следующими показателями:
1. Установившаяся ошибка = 0.
2.
Быстродействие
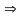 минимальное
время нарастания и время установления.
минимальное
время нарастания и время установления.
3.
0,1%
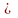 относительное перерегулирование <
2%.
относительное перерегулирование <
2%.
4. Относительный выброс ниже установившегося значения < 2%.
Показатели
(3) и (4) требуют, чтобы после того как в
момент
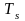 переходная
характеристика войдёт в зону 2% от
установившегося значения, она всё время
оставалась в пределах этой зоны.
переходная
характеристика войдёт в зону 2% от
установившегося значения, она всё время
оставалась в пределах этой зоны.
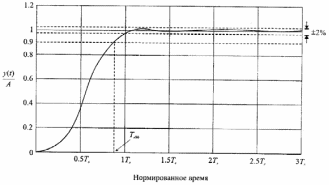
Рис. 1. Апериодическая реакция системы (А – амплитуда входного ступенчатого
воздействия)
Чтобы
определить коэффициенты передаточной
функции замкнутой системы
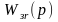 ,
при которых реакция будет иметь
апериодический характер, приведём
сначала эту передаточную функцию к
нормированному виду. Покажем это на
примере системы третьего порядка:
,
при которых реакция будет иметь
апериодический характер, приведём
сначала эту передаточную функцию к
нормированному виду. Покажем это на
примере системы третьего порядка:
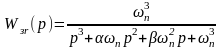 .
(1)
.
(1)
Разделим
числитель и знаменатель на
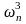 :
:
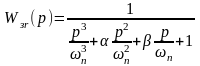 .
(2)
.
(2)
Введя
обозначение
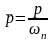 ,
получим:
,
получим:
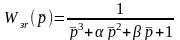 .
(3)
.
(3)
Выражение
(3) – это нормированная передаточная
функция замкнутой системы третьего
порядка. Тем же самым способом определяются
и нормированные передаточные функции
систем более высокого порядка.
Коэффициентам
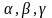 и т.д. придаются значения, при которых
система будет иметь апериодическую
реакцию. Коэффициенты, приведенные в
табл. 1, выбраны таким образом, чтобы
получить апериодическую реакцию и
минимизировать время установления и
время нарастания до 100% от заданного
значения. В выражении (3) фигурирует
нормированная переменная
и т.д. придаются значения, при которых
система будет иметь апериодическую
реакцию. Коэффициенты, приведенные в
табл. 1, выбраны таким образом, чтобы
получить апериодическую реакцию и
минимизировать время установления и
время нарастания до 100% от заданного
значения. В выражении (3) фигурирует
нормированная переменная
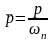 .
Поэтому частота
.
Поэтому частота
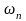 определяется
по заданному времени установления или
времени нарастания. Так, если в системе
третьего порядка необходимо иметь время
установления, равное 1,2 с, то согласно
табл. 1 мы имеем нормированное время
установления
определяется
по заданному времени установления или
времени нарастания. Так, если в системе
третьего порядка необходимо иметь время
установления, равное 1,2 с, то согласно
табл. 1 мы имеем нормированное время
установления
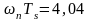 .
.
Отсюда
находим частоту
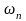 :
:
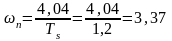 .
.
Таблица 1
Коэффициенты и параметры переходной характеристики системы с апериодической реакцией
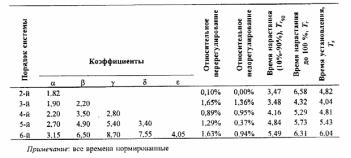
После этого можно записать передаточную функцию замкнутой системы в виде (1).
При синтезе системы с апериодической реакцией выбирается тип корректирующего устройства и записывается выражение для передаточной функции замкнутой системы. Эта передаточная функция приводится к виду (1), после чего нетрудно определить параметры корректирующего устройства.
Пример 5
Рассмотрим
систему с единичной обратной связью,
корректирующим устройством
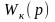 и
предшествующим фильтром.
и
предшествующим фильтром.
Объект имеет передаточную функцию
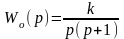 ,
,
а корректирующее устройство – передаточную функцию
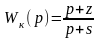 .
.
Предшествующий фильтр должен иметь передаточную функцию
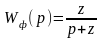 .
.
В этом случае передаточная функция замкнутой системы с предшествующим фильтром равна
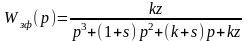 .
.
С
помощью табл.1 находим требуемые значения
коэффициентов:
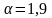 и
и
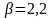 .
.
Если
время установления (по критерию 2%) должно
быть равно 2 с, то
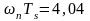 и, следовательно,
и, следовательно,
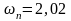 .
Тогда желаемый характеристический
полином замкнутой системы будет иметь
вид:
.
Тогда желаемый характеристический
полином замкнутой системы будет иметь
вид:
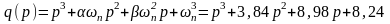 .
.
Отсюда
находим, что s
= 2,84, z
= 1,34 и k
= 6,14. Переходная характеристика системы
имеет значения
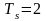 с,
с,
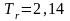 с
и
с
и
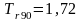 с.
с.
Приложение 5
Реализация цифровых регуляторов
Цифровые регуляторы могут быть реализованы в виде импульсных фильтров (на базе четырехполюсников в сочетании с квантователями и экстраполяторами), на основе микроЭВМ и цифровых устройств.
Передаточная
функция цифрового регулятора в
соответствии с рис.7.4б будет 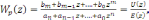
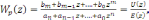 (7.13)
(7.13)
причем всегда должно быть n≥m.
Разделим числитель на знаменатель на zn. Тогда для предельного случая n=m
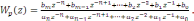
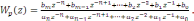 (7.14)
(7.14)
Если a0=1, то из (7.14) можно получить линейный алгоритм работы цифрового управляющего устройства:
u[k]=b0e[k]+b1e[k-1]+…+bme[k-n]- (a1u[k-1]+a2u[k-2]+…+anu[k-n]). (7.15)
Из полученных соотношений можно установить, что цифровой регулятор оказывается физически реализуемым, если в (7.14) нет слагаемых с положительной степенью z. Наличие хотя бы одного члена в (7.14) с положительной степенью z означает «упреждение», т.е. показывает, что выходной сигнал опережает входной. В равной степени это относится и к слагаемым уравнения (7.15), т.е. значение u[k] будет определяться значениями опережающих его слагаемых u[k+1] и e[k+1].
Условием физической реализуемости цифрового регулятора, таким образом, является выполнение условия n≥m. Кроме того, при n=m знаменатель (7.14) не должен иметь сомножителя z-1 при b0 ≠0 , т.е. должно быть также a0≠0.
К цифровым регуляторам предъявляются требования к точности реализации параметров при их вычислении с ограниченной разрядностью процессоров.
Для обеспечения устойчивости регуляторов должно выполняться условие расположения полюсов их передаточной функции внутри единичной окружности на комплексной плоскости.
Передаточная функция цифрового регулятора обычно реализуется в виде программы ЭВМ, реализуемых методами прямого, последовательного и параллельного программирования.
При прямом программировании из передаточной функции (7.14) запишем уравнение в форме обратного преобразования:
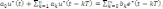
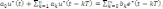 (7.16)
(7.16)
решением которого будет:
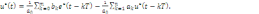
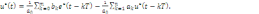 (7.17)
(7.17)
В общем виде уравнение (7.17) может быть представлено, как разность двух групп слагаемых входного и выходного сигналов:
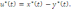
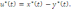 (7.18)
(7.18)
Для последовательного программирования передаточную функцию регулятора представляют в виде произведения простейших передаточных функций, каждая из которых реализуется простейшими программами:
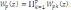
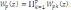 (7.19)
(7.19)
где p – наибольшее из чисел n и m. Для каждой простейшей программы используется метод прямого программирования.
При
параллельном
программировании
передаточная функция (7.14) представляется
в виде 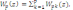
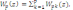 (7.20)
(7.20)
где p – наибольшее из чисел n и m. Здесь также каждая из передаточных функций может быть реализована методом прямого программирования.
Пример 1
Пусть передаточная функция цифрового регулятора имеет вид:
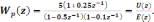
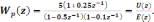
Регулятор
является физически реализуемым (n=2,
m=1
при
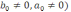
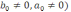 и
устойчивым (полюсы z1=0.5,
z2=0.1).
и
устойчивым (полюсы z1=0.5,
z2=0.1).
-
Прямое программирование.
Из передаточной функции запишем линейное уравнение регулятора:
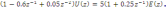
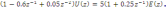
Выразим обратное z- преобразование к обеим частям уравнения:
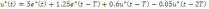
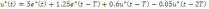
Применяя метод прямой (непосредственной) декомпозиции к предыдущему уравнению
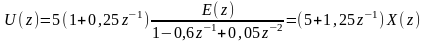 ,
,
где
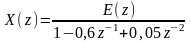 или
или
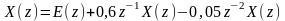 ,
,
получим систему:
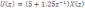
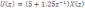


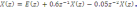
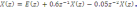
Структура решения данной системы уравнений приведена на рис.1.
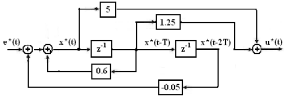
Рис.1. Прямое программирование передаточной функции
-
Последовательное программирование.
Передаточную функцию регулятора запишем в виде произведения двух функций, например, вида:
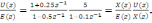
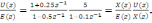
Программирование выполним, представив произведение передаточных функций системой уравнений:
X(z)=(1+0.25z-1)E(z)+0.5z-1X(z)
U(z)=5X(z)+0.1z-1U(z).
Структурная схема решения системы приведена на рис.7.9.
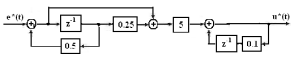
Рис.7.9 Последовательное программирование передаточной функции
-
Параллельное программирование.
Разложим
передаточную функцию регулятора на
сумму простейших: 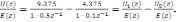
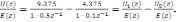
Составим систему уравнений, U(z)=U1(z)-U2(z)
U1(z)=9.375E(z)+0.5z-1U1(z)
U2(z)= 4.375E(z)+0.1z-1U2(z),
структурная схема решения системы приведена на рис.7.10.
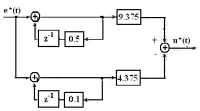
Рис.2. Параллельное программирование передаточной функции
Для преобразования сложной дискретной передаточной функции к алгебраической сумме элементарных используйте две леммы высшей
алгебры:
Лемма
1. Пусть
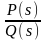 -
правильная рациональная дробь с
действительными
-
правильная рациональная дробь с
действительными
коэффициентами и пусть S1
есть вещественный корень полинома Q(s)
кратности r, тогда существует такое число А и такой полином P1(s), что
справедливо равенство
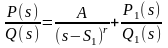 ,
,
где
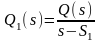 ;
при этом
;
при этом
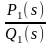 -
правильная рациональная дробь.
-
правильная рациональная дробь.
Лемма
2. Пусть
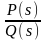 -
правильная рациональная дробь с
действительными
-
правильная рациональная дробь с
действительными
коэффициентами
и Q(s)=(s2+ps+q)m∙V(s),
где
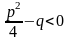 ,
корни полинома не
,
корни полинома не
являются корнями полинома V(s), V(s) не делится нацело на (s2+ps+q).
Тогда найдутся такие вещественные числа M и N и такой полином P1(s),что
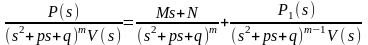 ,
,
где второе слагаемое будет также правильная рациональная дробь.
Пример:
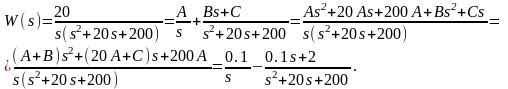
Здесь использован метод неопределённых коэффициентов:
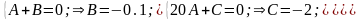
Примечание:
1.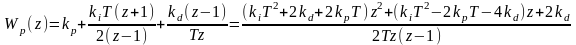 .
.
2. Теорема о разложении многочлена на множители:
«Каждый
(действительный или комплексный)
многочлен
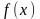 степени
степени
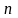 относительно
относительно
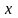 может быть единственным способом
представлен в виде произведения
постоянной и
может быть единственным способом
представлен в виде произведения
постоянной и
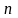 линейных множителей
линейных множителей
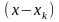 ,
именно
,
именно
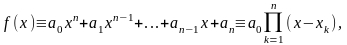
где
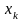 -
корни многочлена
-
корни многочлена
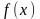 ;
корню
;
корню
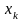 кратности
кратности
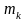 соответствует
соответствует
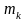 множителей
множителей
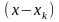 .
Каждая пара множителей
.
Каждая пара множителей
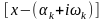 и
и
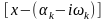 ,
соответствующая паре комплексных
сопряжённых корней
,
соответствующая паре комплексных
сопряжённых корней
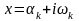 и
и
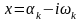 ,
,
может
быть объединена в действительный
квадратный множитель
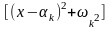 ».
».
Пример 2
Передаточная функция аналогового корректирующего устройства имеет вид
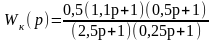 .
.
Определите дискретную передаточную функцию цифрового алгоритма управления объектом путём преобразования аналогового регулятора в цифровой при периоде квантования сигналов T=0,02с. Проверьте адекватность преобразования по амплитудно-фазовым частотным характеристикам непрерывного и цифрового корректирующих звеньев. Составьте программу работы ЦВМ на основании полученной дискретной передаточной функции и постройте структурную схему реализации алгоритма дискретного корректора.
Решение
Для получения дискретного аналога корректирующего алгоритма в форме обратных разностей используем аппроксимационную формулу Тастина
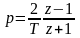 ,
,
приведём
первый коэффициент знаменателя к 1 и
разделим числитель и знаменатель
дискретной передаточной функции на
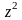 :
:
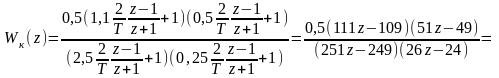

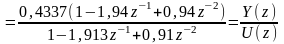 .
.
Из последнего выражения
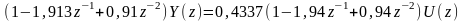 ,
,
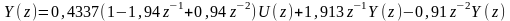 .
.
Обратное Z-преобразование этого выражения – рекуррентная форма дискретного управляющего алгоритма:
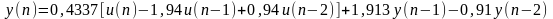 .
.
Структурная схема реализации полученного алгоритма в микроЭВМ представлена на рис.1.
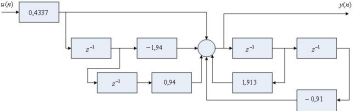
Рис.1. Структурная схема дискретного управляющего алгоритма
Греческий алфавит
|
Название буквы |
Прописная |
Строчная |
Название буквы |
Прописная |
Строчная |
|
Альфа |
|
|
Ню |
|
|
|
Бета |
|
|
Кси |
|
|
|
Гамма |
|
|
Омикрон |
|
|
|
Дельта |
|
|
Пи |
|
|
|
Эпсилон |
|
|
Ро |
|
|
|
Дзета |
|
|
Сигма |
|
|
|
Эта |
|
|
Тау |
|
|
|
Тета |
|
|
Ипсилон |
|
|
|
Йота |
I |
|
Фи |
|
|
|
Каппа |
|
|
Хи |
|
|
|
Лямбда |
|
|
Пси |
|
|
|
Мю |
|
|
Омега |
|
|
Список рекомендуемой литературы
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления: Учебник – СПб: Изд-во «Профессия», 2003-2007.-752 с.
2. Бесекерский В.А. Цифровые автоматические системы.- М.:Наука,1976.-576с.
3. Васильев Е.М., Коломыцев В.Г. Теория автоматического управления. Нелинейные системы: Учебное пособие – Пермь: Изд-во ПНИПУ, 2011.-115с.
4. Васильев Е.М., Коломыцев В.Г. Теория автоматического управления. Дискретные системы: Учебное пособие – Пермь: Изд-во ПНИПУ, 2012.-152с.
5. Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. — М.: Горячая линия-Телеком, 2009.-608с.
6. Диркс Г.Г., Коломыцев В.Г. Проектирование микропроцессорных систем автоматического управления. Ч.1. Синтез систем автоматического управления: Учебное пособие - Пермь: Изд-во ПГТУ, 1997.-175с.
7. Дорф Р., Бишоп Р. Современные системы управления:Учебник-М.:Изд-во «Лаборатория Базовых Знаний», 2002-2004.- 832 с.
8. Душин С.Е., Зотов Н.С., Имаев Д.Х. и др. Под ред. В.Б.Яковлева. Теория автоматического управления: Учебник - М.: Изд-во «Высшая школа», 2005.-567 с.