Файл: Контрольные работы. Теория автоматического управления.docx
ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Методичка
Дисциплина: Теория автоматического управления
Добавлен: 19.10.2018
Просмотров: 5341
Скачиваний: 88
Высокочастотные асимптоты ЛАЧХ (справа от наибольшей сопрягающей частоты) проводят в требуемом диапазоне частот.
Примечания
-
Для построения ЛАЧХ звена второго порядка используются приведенные характеристики в технической литературе или строятся по точкам вблизи i=1/Ti, вдали с асимптотами левой 0 дБ/дек , правой -40 дБ/дек для колебательного звена и +40 дБ/дек для звена дифференцирующего второго порядка.
-
Правило построения ЛЧХ систем с неминимально-фазовыми звеньями остаётся тем же.
-
ЛФЧХ строятся по точкам, рассчитанным аналитически.
Пример
Пусть задана передаточная функция объекта
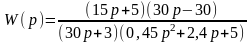 .
.
Требуется построить асимптотическую ЛАЧХ объекта.
1. Выделение элементарных звеньев.
Вынесем множитель из каждой скобки так, чтобы свободный член в этой скобке был равен 1:
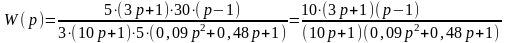 .
.
Корни квадратного трёхчлена в знаменателе комплексно-сопряжённые, поэтому можно представить заданную передаточную функцию в виде произведения передаточного коэффициента и четырёх передаточных функций элементарных звеньев:
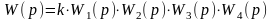 ,
,
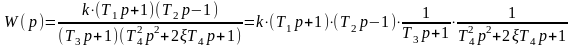 ,
,
где
 .
.
Звенья
с передаточными функциями
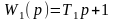 и
и
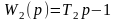 - идеальные звенья с введением производной,
второе из них – неминимально - фазовое.
Звено с передаточной функцией
- идеальные звенья с введением производной,
второе из них – неминимально - фазовое.
Звено с передаточной функцией
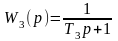 -
апериодическое звено, а звено с
-
апериодическое звено, а звено с
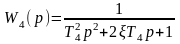 -
колебательное, поскольку
-
колебательное, поскольку
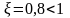 .
.
2. Определение сопрягающих частот.
Сопрягающие
частоты – это точки излома ЛАЧХ. Они
определяются как
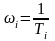 .
Таким образом,
.
Таким образом,
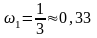 рад/с,
рад/с,
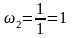 рад/с,
рад/с,
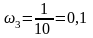 рад/с,
рад/с,
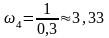 рад/с.
рад/с.
Поскольку при построении ЛАЧХ на оси абсцисс откладывается lgω, вычислим десятичные логарифмы этих частот:
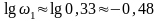 ,
,
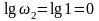 ,
,
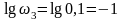 ,
,
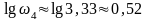 .
.
3. Построение ЛАЧХ.
Отметим найденные точки излома ЛАЧХ на оси абсцисс:
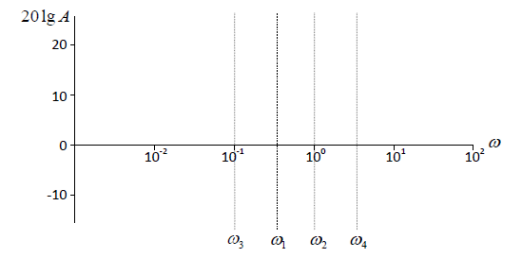
Поскольку
интегрирующие и дифференцирующие звенья
в системе отсутствуют, на низких частотах
(примерно до первой сопрягающей частоты
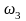 )
система имеет постоянное усиление,
равное k=10.
Учитывая, что амплитудная характеристика
откладывается в логарифмическом масштабе
(в децибеллах) получаем
)
система имеет постоянное усиление,
равное k=10.
Учитывая, что амплитудная характеристика
откладывается в логарифмическом масштабе
(в децибеллах) получаем
20lgk=20lg10=20
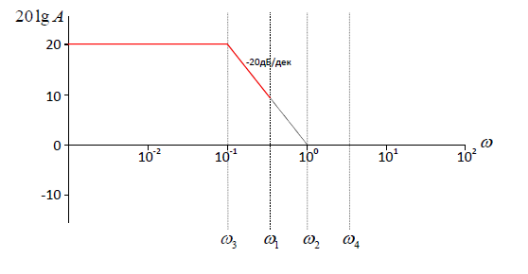
и можно сразу нарисовать начальный участок ЛАЧХ:
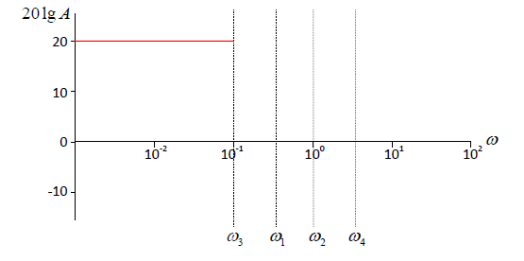
На
частоте
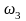 вступает в действие апериодическое
звено, которое даёт наклон -20 дБ/дек, в
интервале от
вступает в действие апериодическое
звено, которое даёт наклон -20 дБ/дек, в
интервале от
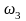 до
до
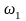 график спускается вниз на
график спускается вниз на

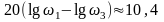 дБ,
поэтому ордината для частоты
дБ,
поэтому ордината для частоты
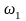 равна
равна
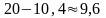 дБ:
дБ:
На
частоте
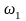 идеальное звено с введением производной
добавляет наклон +20 дБ/дек, таким образом,
общий наклон становится равен нулю:
идеальное звено с введением производной
добавляет наклон +20 дБ/дек, таким образом,
общий наклон становится равен нулю:
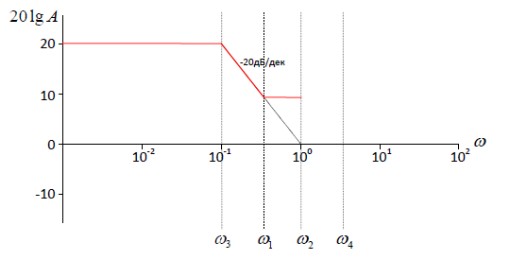
На
частоте
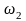 неминимально – фазовое идеальное звено
с введением производной ещё добавляет
наклон +20 дБ/дек, таким образом, общий
наклон становится равен +20 дБ/дек. В
интервале от
неминимально – фазовое идеальное звено
с введением производной ещё добавляет
наклон +20 дБ/дек, таким образом, общий
наклон становится равен +20 дБ/дек. В
интервале от
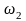 до
до
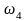 график поднимается на
график поднимается на
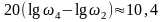 дБ,
поэтому ордината для частоты
дБ,
поэтому ордината для частоты
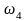 равна 9,6+10,4
равна 9,6+10,4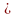 20
дБ:
20
дБ:
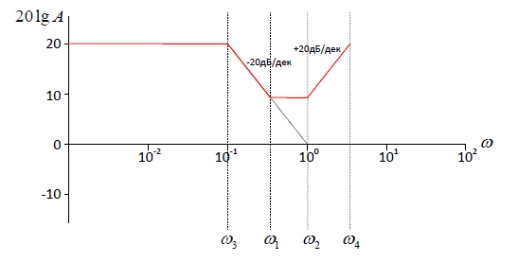
Наконец,
на частоте
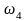 колебательное звено добавляет наклон
-40 дБ/дек, таким образом, общий наклон
становится равен -20 дБ/дек:
колебательное звено добавляет наклон
-40 дБ/дек, таким образом, общий наклон
становится равен -20 дБ/дек:
Приложение 3
Пример рекомендуемой последовательности действий при анализе
устойчивости системы
Пусть задана структурная схема (рис. 5) и параметры исследуемой системы.
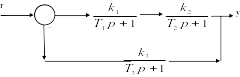
Рис. 5. Структурная схема исследуемой системы
Алгоритм исследования устойчивости замкнутой САУ:
-
определяем передаточную функцию замкнутой системы
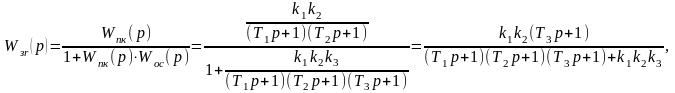 где
Wпк(p)
– передаточная функция прямого канала
системы; Wос(p)
– передаточная функция обратной связи;
где
Wпк(p)
– передаточная функция прямого канала
системы; Wос(p)
– передаточная функция обратной связи;
-
записываем характеристическое уравнение замкнутой системы:
(Т1р+1)(Т2р+1)(Т3р+1)+k1k2k3=0;
после преобразования этого выражения получим:
Т1Т2Т3р3+(Т1Т2+Т1Т3+Т2Т3)р2+(Т1+Т2+Т3)р+(1+k1k2k3)=0;
обозначим:
а0=T1T2T3;
a1=Т1Т2+Т1Т3+Т2Т3;
а2=Т1+Т2+Т3;
а3=1+k1k2k3;
тогда выражение примет стандартную форму:
а0р3+а1р2+а2р+а3=0;
-
условия устойчивости замкнутой системы 3-го порядка:
-
а0>0, a1>0, a2>0, a3>0 (условие Рауса);
-
a1a2>a0a3 (условие Гурвица);
если условия устойчивости имеют место, то система устойчива;
-
система на границе устойчивости, если выполняется равенство в условии Гурвица, отсюда определяется критическая величина передаточного коэффициента разомкнутой системы:
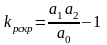 ;
;
-
заключение об устойчивости системы.
Приложение 4
Методы настройки параметров ПИД – регулятора
ПИД – регулятор был изобретён в 1910 году. Долгое время настройка параметров регулятора осуществлялась эвристическим ручным методом, основанным на интуиции и изобретательстве инженеров.
В 1942 году американские учёные J.G. Ziegler и N.B. Nichols (США, г. Рочестер, штат Нью-Йорк) при исследовании систем с ПИД – регуляторами обнаружили две закономерности:
Оптимальная зона пропорциональности П – регулятора в два раза меньше величины зоны пропорциональности, при которой в САУ начинается автоколебательный процесс;
Время изодрома Ti и время предварения Td зависят от периода возникающих автоколебаний.
В качестве критерия оптимальности принята величина декремента затухания
D = 0,2-0,3. Декремент затухания D выражается через отношение двух амплитуд, отстоящих друг от друга на половину периода,
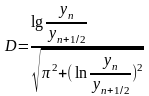 .
.
Зиглер и Никольс предложили два метода настройки ПИД – регулятора: первый основан на параметрах переходной характеристики, второй на частотных характеристиках объекта управления. Точность настройки параметров регулятора и недостатки обоих методов Зиглера – Никольса одинаковы.
1. Настройка параметров ПИД – регулятора по временному модифицированному методу Зиглера – Никольса.
Пусть известно математическое описание объекта второго порядка в форме передаточной функции
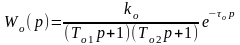 .
.
Требуется найти параметры ПИД - регулятора по параметрам переходной характеристики объекта.
Алгоритм расчёта:
1. Определяем переходную характеристику объекта и её производную, используя модель объекта в Simulink:
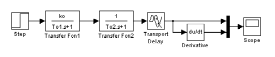
2. По максимальному значению производной находим точку перегиба переходной характеристики и проводим через неё касательную к переходной характеристике путём смещения характеристики интегрирующего звена ki/p изменением параметра a с помощью модели в Simulink (рис. 2), где ki = max[dh(t)/dt].
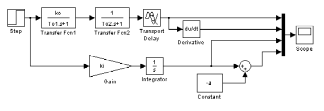
3. Определяем численные значения параметров a и L по графику переходной характеристики и касательной к ней в точке перегиба.
4. Определяем параметры ПИД – регулятора по формулам таблицы 1 [ ].
Таблица 1. Формулы для расчёта параметров ПИД – регулятора по временному методу Зиглера - Никольса
-
Расчёт по
отклику на
скачок
Регулятор
k
Tи
Tд
П
1/a
ПИ
0,9/a
3L/k
ПИД
1,2a
2L/k
0,5Lk
Примечание: система обозначений параметров регулятора соответствует уравнению
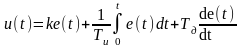 .
.
5. Строим модель системы с ПИД – регулятором в Simulink и проводим исследование САУ.
Пример 1
Передаточная функция объекта имеет вид
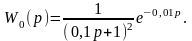
Определить настройки параметров ПИД-регулятора по параметрам отклика объекта на единичный скачок.
1. Составляем модель исследования разомкнутой исходной системы в Simulink (рис. 1).
В состав алгоритмической структуры входит модель объекта, модуль формирования производной переходной характеристики, интегратор с передаточным коэффициентом, равным величине экстремума импульсной переходной характеристики и модуль сдвига переходной характеристики идеального интегрирующего звена так, чтобы она проходила через точку перегиба переходной характеристики объекта.
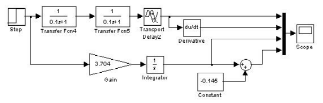
Рис. 1. Алгоритмическая структура для исследования разомкнутой исходной системы в Simulink
2. По отклику модели определяем базовые расчётные параметры: a = 0,145 - величина смещения переходной характеристики интегрирующего звена в точку перегиба переходной характеристики объекта (точку перегиба переходная характеристика объекта и максимум производная этой характеристики h’max = 3,704 проходят в один и тот же момент tэкстр. = 0,1205 ), L = 0,04- величина отрезка на оси времени, отсекаемого касательной к переходной характеристике в точке перегиба. Графики исследуемой модели приведены на рис.2.
3. Составляем скрипт в Matlab для расчёта параметров ПИД – регулятора:
a=0.145;
L=0.04;
k=1.2/a
Ti=2*L/k
Td=0.5*L*k
ki=1/Ti
kd=Td
и определяем настройки регулятора:
k = 8.2759, Ti = 0.0097c, Td =0.1655c, ki = 103.4483c-1, kd =0.1655c.
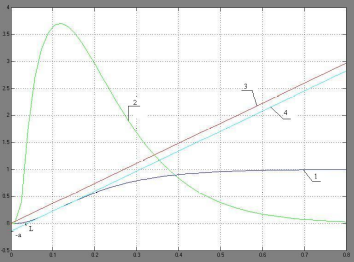
Рис. 2. Графики исследуемой модели разомкнутой исходной системы: 1 - переходная характеристика объекта, 2 – производная переходной характеристики объекта, 3 - переходная характеристика интегрирующего звена, передаточный коэффициент которого равен максимуму производной переходной характеристики объекта ( kи = 3,704), 4 - смещённая в точку перегиба переходной характеристики объекта переходная характеристика интегрирующего звена
4. Строим модель для исследования системы в Simulink (рис. 3).
На рис. 3 изображены (сверху – вниз) модели исследуемой системы с настройками регулятора по методу Зиглера – Никольса, системы с ручной настройкой параметров регулятора, объекта и модель формирования касательной в точке перегиба переходной характеристики объекта.
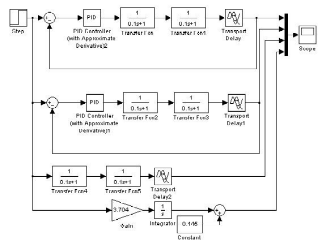
Рис. 3. Алгоритмическая структура для исследования скорректированной системы в Simulink
5. Снимаем переходные характеристики модели, изображенной на рис. 3, где обозначены: 1 – переходная характеристика объекта, 2 – касательная к переходной характеристике объекта в точке перегиба, 3 – переходная характеристика системы при настройке регулятора по методу Зиглера – Никольса, 4 - переходная характеристика системы при ручной настройке регулятора ( k = 15, Ti = 0,013c, Td = 0,525c)
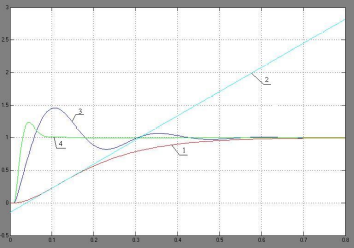
Рис. 4. Графики переходных характеристик модели, изображенной на рис. 3
2. Настройка параметров ПИД – регулятора по частотному методу Зиглера – Никольса.
Пусть известно математическое описание объекта управления в форме передаточной функции
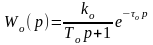 или
или
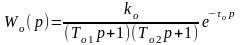 .
.
Требуется найти параметры ПИД - регулятора по частотному методу Зиглера –
Никольса.
Алгоритм расчёта:
1.
Определяем по АФХ и ЛЧХ объекта частоту
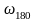 ,
при которой фазовый сдвиг
,
при которой фазовый сдвиг
объекта равен -180о.
2.
Определяем передаточный коэффициент
объекта
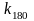 на частоте
на частоте
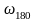 .
.
3.
Определяем период колебаний
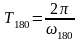 .
.
4. По табл. 2 Зиглера – Никольса определяем параметры ПИД – регулятора,
используя
полученные данные
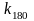 и
и
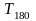 .
.
Таблица 2. Формулы для расчёта параметров ПИД – регулятора по частотному методу Зиглера - Никольса
-
Расчёт по
частотным
параметрам
Регулятор
k
Tи
Tд
П
0,5/
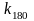
ПИ
0,4/
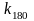
0,8
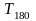 /k
/kПИД
1,6/
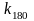
0,5
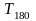 /k
/k0,125
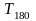 k
k
Примечание: система обозначений параметров регулятора соответствует уравнению
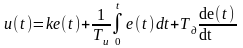 .
.
5. Составляем в Matlab модели замкнутых исходной и с ПИД – регулятором систем
для построения переходных характеристик, по которым оцениваем устойчивость и
показатели качества.
Пример 2
Передаточная функция объекта имеет вид
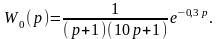
Определить настройки параметров ПИД-регулятора по частотным параметрам объекта управления.
1. Составляем модель в форме скрипта Matlab для определения АФХ и ЛЧХ объекта по его передаточной функции.
numo=[1];
deno=[10 11 1];
Wo=tf(numo,deno)
[nums,dens]=pade(0.3,2)
Ws=tf(nums,dens)
Wir=Wo*Ws
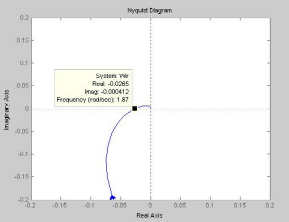
nyquist(Wir)
%margin(Wir)
2.
Определяем АФХ объекта и находим
параметры
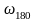 =1,87с-1
и
=1,87с-1
и
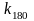 =|Real|=0,0265.
=|Real|=0,0265.
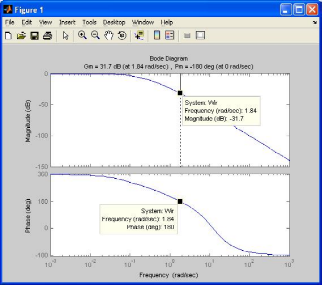
3.
Определяем ЛЧХ объекта и находим
параметры
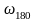 =1,84с-1
и
=1,84с-1
и
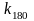 =10-31,7/20=
0,026.
=10-31,7/20=
0,026.
Параметры объекта, найденные по ЛЧХ, точнее параметров АФХ, поэтому принимаем их за основу.
4.
Составляем скрипт для определения
параметров ПИД – регулятора по полученным
параметрам ЛЧХ:
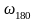 =1,84с-1
и
=1,84с-1
и
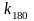 =10-31,7/20=
0,026. Расчётные формулы параметров ПИД
– регулятора приведены в таблице 2
алгоритма расчёта.
=10-31,7/20=
0,026. Расчётные формулы параметров ПИД
– регулятора приведены в таблице 2
алгоритма расчёта.
k180=0.026;
w180=1.84;
T180=2*pi/w180
kn=0.6/k180
Tu=0.5*T180/kn
ku=1/Tu
Td=0.125*T180*kn
kd=Td
Расчётные параметры ПИД – регулятора: kn = 23.0769, ku = 13.5159, kd = 9.8503.
5. Составляем скрипт для определения переходных характеристик исходной и скорректированной замкнутых систем.
kp=23.0769;
ki=13.5159;
kd=9.8503;
numo=[1];
deno=[10 11 1];
Wo=tf(numo,deno)
[nums,dens]=pade(0.3,2)
Ws=tf(nums,dens)
numi=[ki];
deni=[1 0];
Wi=tf(numi,deni)
numd=[kd 0];
dend=[1];
Wd=tf(numd,dend)
Wsr=minreal(Wo*Ws/(1+Wo*Ws))
step(Wsr)
%Wsrpid=minreal((kp+Wi+Wd)*Wo*Ws/(1+(kp+Wi+Wd)*Wo*Ws))
%step(Wsrpid)
6. Определяем переходную характеристику исходной (нескорректированной) системы, произведя «Пуск» скрипта п.5 в Matlab.
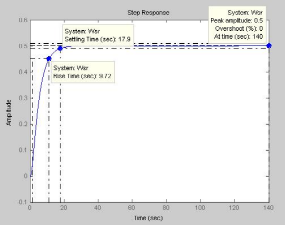
7. Определяем переходную характеристику скорректированной системы, сняв знак % в последних двух строках скрипта и установив % в двух предыдущих строках.
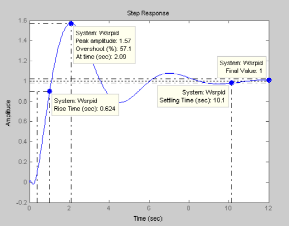
Показатели качества систем приведены на графиках.
3. Настройка параметров ПИД – регулятора по методу CHR (Chien – Hrones – Reswick).
Авторы этого метода использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20% - ного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера – Никольса.
Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки, решая задачу качества регулирования, вторая – при наблюдении отклика на внешние возмущения, решая задачу ослабления внешних возмущений.
Если важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы.
В этом методе объект аппроксимирован моделью первого порядка с задержкой:
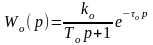 .
.
Для
расчёта параметров регулятора используются
параметры переходной характеристики
объекта:
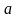 и
и
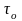 .
.
Параметр
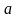 определяется из выражения:
определяется из выражения:
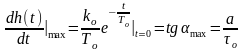 ,
отсюда
,
отсюда
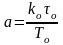 ,
,
или из графика переходной характеристики объекта.
Формулы для расчёта параметров регулятора приведены в таблицах 3 и 4.
Таблица 3
Формулы для расчёта коэффициентов регулятора по отклику на изменение уставки метода CHR
-
Без перерегулирования
С 20% - ным перерегулированием
Регулятор
k
Ти
Тд
k
Tи
Тд
П
0,3/а
0,7/a
ПИ
0.35/a
1,2
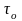 /k
/k0,6/a
1,0
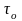 /k
/kПИД
0,6/a
10
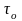 /k
/k0,5
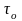 k
k0,95/a
1,4
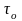 /k
/k0,47
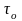 k
k
Таблица 4
Формулы для расчёта коэффициентов регулятора по отклику на внешние воздействия метода CHR