Добавлен: 19.10.2018
Просмотров: 3428
Скачиваний: 9
41
Контрольные вопросы
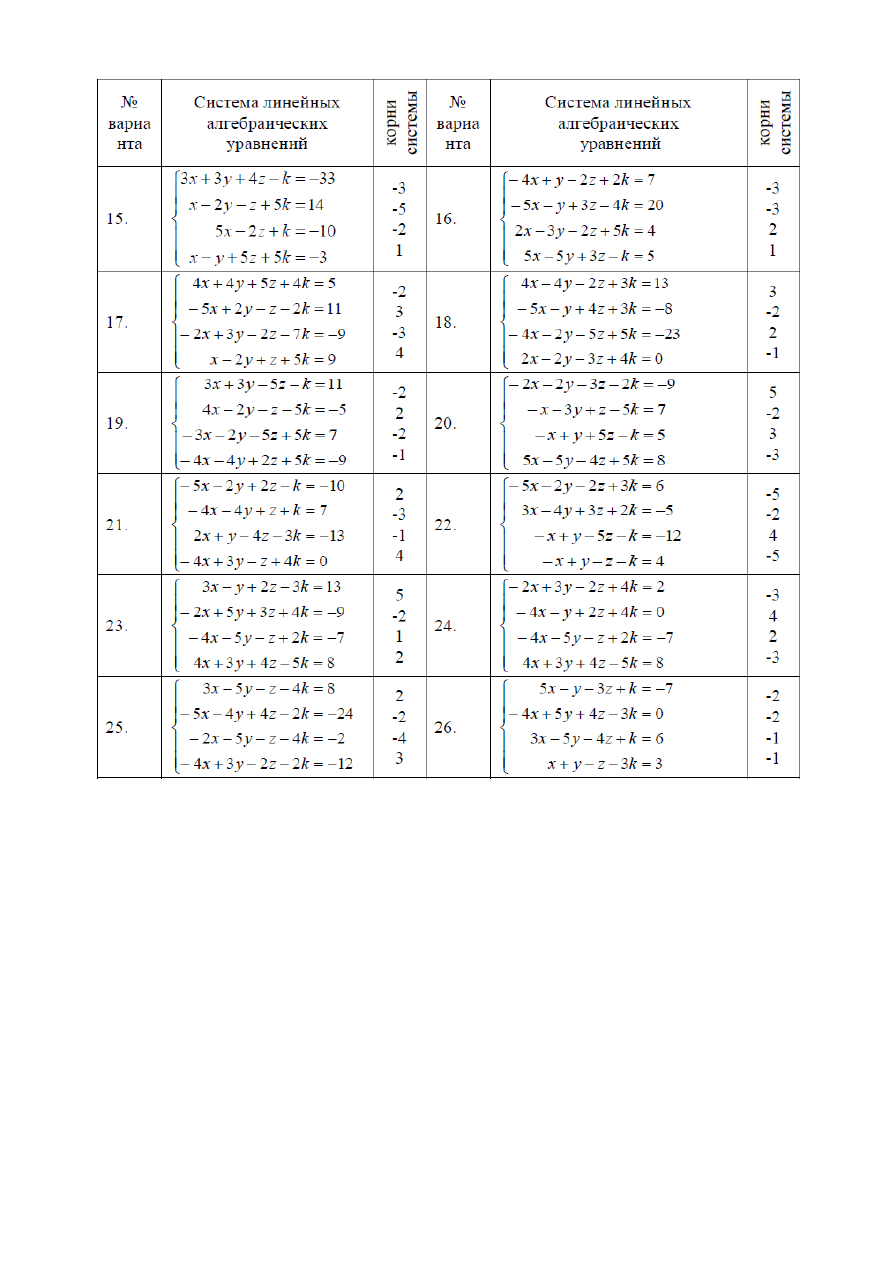
1.
Основные понятия алгебры матриц. Действия с матрицами. Норма
матрицы. Транспонированная и обратная матрицы.
2.
Методы решения систем линейных алгебраических уравнений. Метод
исключения Гаусса.
3.
Вычисление обратной матрицы методом Гаусса.
4.
Вычисление определителя методом Гаусса.
5.
Итерационные методы решения систем линейных алгебраических
уравнений. Метод Якоби. Условие сходимости итераций.
6.
Итерационные методы решения систем линейных алгебраических
уравнений. Метод Гаусса-Зейделя. Условие сходимости итераций.
7.
Метод релаксации решения системы линейных алгебраических уравнений.
Лабораторная работа №3
Тема: Численное дифференцирование и интегрирование.

42
1.
Цель работы
Использование численных методов решения задач дифференцирования и
интегрирования.
2.
Учебные вопросы, подлежащие рассмотрению:
−
Постановка задачи.
−
Интерполяционный многочлен Лагранжа и интерполяционный многочлен
Ньютона.
−
Численное дифференцирование с помощью многочленов Лагранжа и
Ньютона.
−
Метод трапеции, метод Симпсона
−
Численное интегрирование методами трапеции и Симпсона (парабол)
3.
Порядок выполнения работы
Задание 1.
Вычислить значение производной функции, заданной таблично, используя
интерполяционные формулы Лагранжа или Ньютона.
Задание 2.
Вычислить интеграл от заданной функции f(x) на отрезке [a,b] при делении
отрезка на 10 равных частей следующими способами 1) по формуле трапеций; 2)
по формуле Симпсона.
Исполнение: применить интерполяционные формулы Лагранжа или Ньютона
используя любой инструментальный пакет для вычисления производной.
Использовать формулы трапеции и формулы Симпсона для вычисления
определенного интеграла.
Оценка: Сопоставление полученных результатов, решаемых различными
методами.
Методические указания
Контрольные вопросы и задания
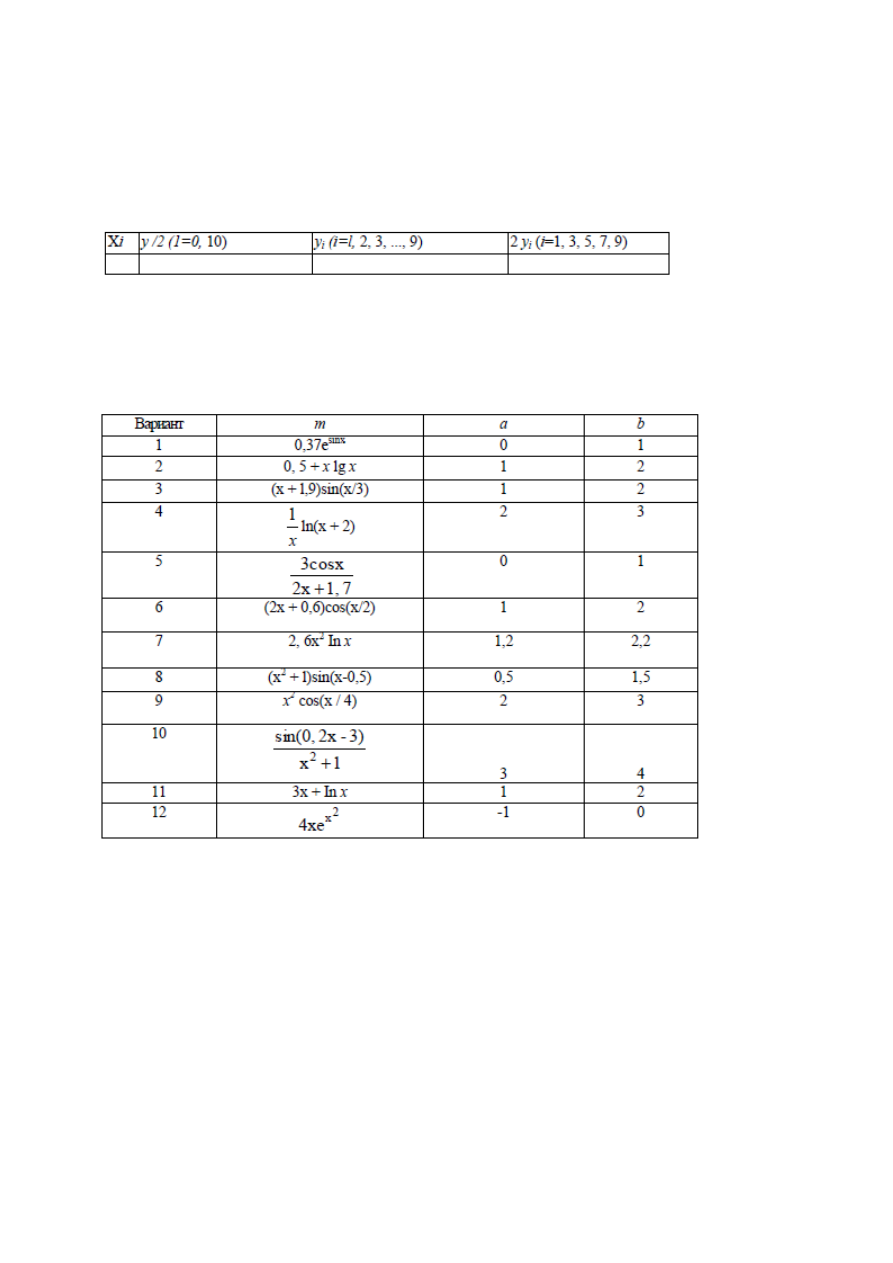
1. Вычислить значение производной функции, заданной таблично, используя
интерполяционные формулы Лагранжа или Ньютона.
Вариант
43
Задание 2.
Вычислить интеграл от заданной функции f(x) на отрезке [a,b] при делении
отрезка на 10 равных частей следующими способами 1) по формуле трапеций; 2)
по формуле Симпсона.
Отрезок интегрирования разбивается на 10 равных частей. Для расчетов
удобно составить единую таблицу значений по схеме:
По каждому из трех столбцов таблицы находятся суммы соответствующих
значений подынтегральной функции (при этом по столбцу у,- для формулы
трапеций находится сумма всех элементов столбца, а для формулы Симпсона —
только с четными индексами).
Вариант
Рассчитать значение определенного интеграла можно с помощью формулы
Ньютона-Лейбница
∫
−
=
b
a
a
F
b
F
dx
x
f
)
(
)
(
)
(
где F(x) – первообразная подинтегральной функции.
В функциях интегрирования в Scilab реализованы различные численные
алгоритмы. Наиболее универсальной командой интегрирования в Scilab
является
[I, err] = intg(a, b, name [,er1 [,er2]]),
где nаmе — имя функции, задающей подынтегральное выражение (функция
может быть задана в виде набора дискретных точек, т.е. таблицей или с

44
помощью внешней функции);
а и b – пределы интегрирования;
erl
и еr2 — абсолютная и относительная точность вычислений
(необязательные параметры).
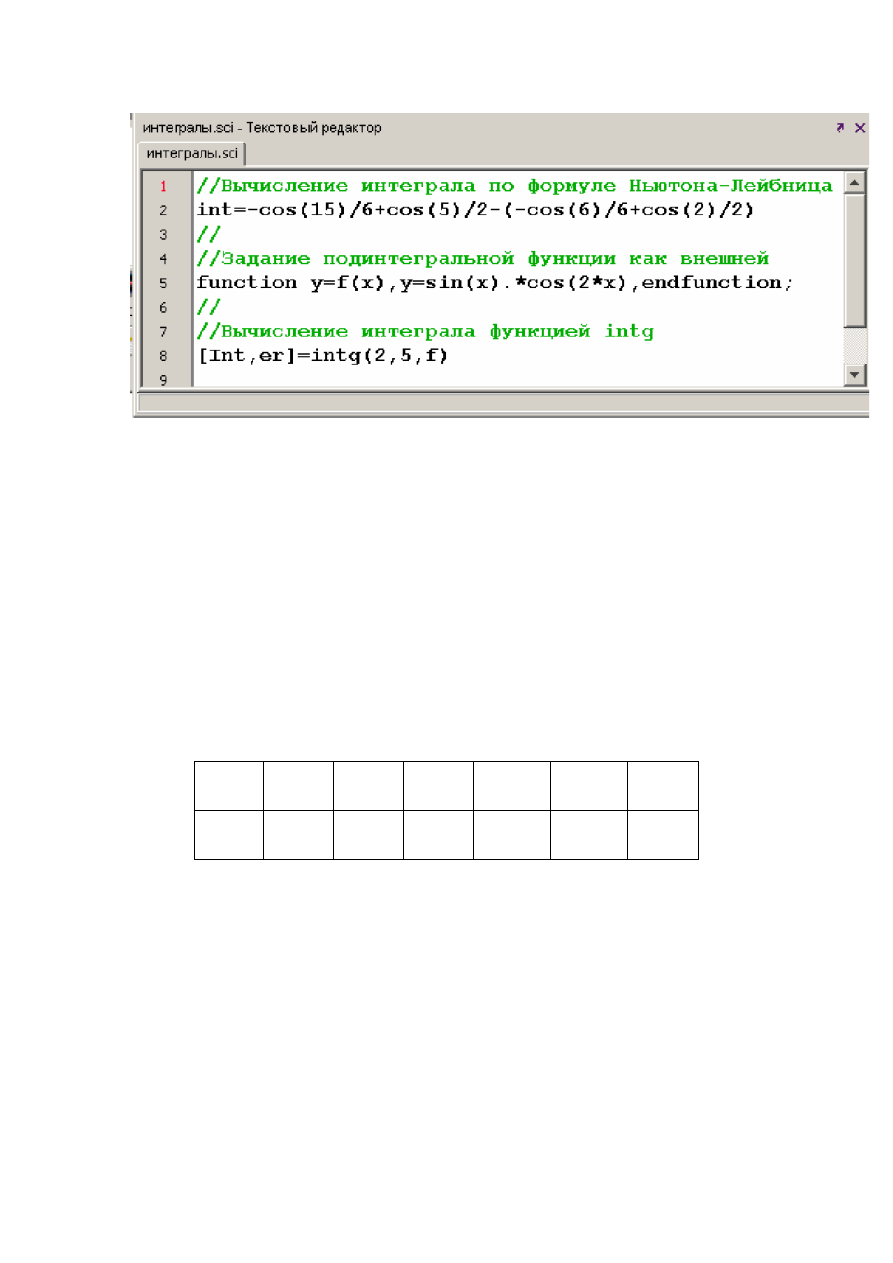
Пример. Вычислить значение интеграла.
∫
⋅
5
2
)
2
cos(
)
sin(
x
x
Первообразной подинтегральной функции является функция
F (x)
= − cos(3x) /6+ cos( x)/2.
Решение, полученное по формуле Ньютона-Лейбница, приведено на рис.
22.
Рис. 22. Вычисление интеграла по формуле Ньютона-Лейбница
При использовании функции intg необходимо вначале задать
подинтегральную функцию как внешнюю. Это можно сделать с помощью
конструкции function … endfunction.
Решение, полученное с помощью функции intg, приведено на рис. 23.
Рис. 23. Использование функции intg
На рис. 24 приведен файл-сценарий вычисления рассматриваемого
интеграла.
45
Рис. 24. Файл-сценарий вычисления рассматриваемого интеграла
Аппроксимация экспериментальных данных
Очень часто, особенно при анализе эмпирических данных возникает
необходимость найти в явном виде функциональную зависимость между
величинами x и y, которые получены в результате измерений.
При аналитическом исследовании взаимосвязи между двумя величинами x и y
производят ряд наблюдений и в результате получается таблица значений:
x
x
1
x
2
…
x
i
…
x
n
y
y
1
y
2
…
y
i
…
y
n
Эта таблица обычно получается как итог каких-либо экспериментов, в
которых
x
i
(независимая величина) задается экспериментатором, а
y
i
получается
в результате опыта. Поэтому эти значения
y
i
будем называть эмпирическими или
опытными значениями.
Между величинами x и y существует функциональная зависимость, но ее
аналитический вид обычно неизвестен, поэтому возникает практически важная
задача - найти эмпирическую формулу