Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 132
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 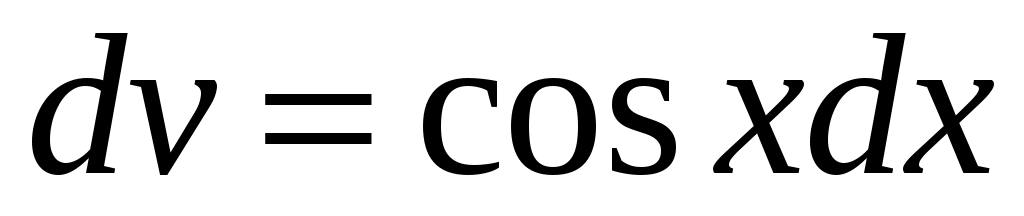 ,
, 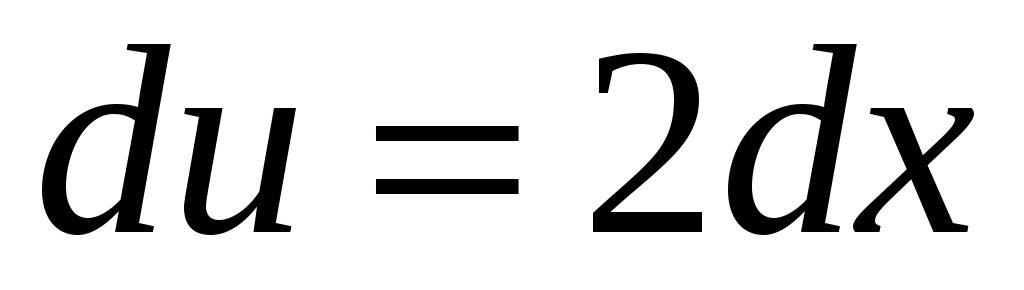 ,
, 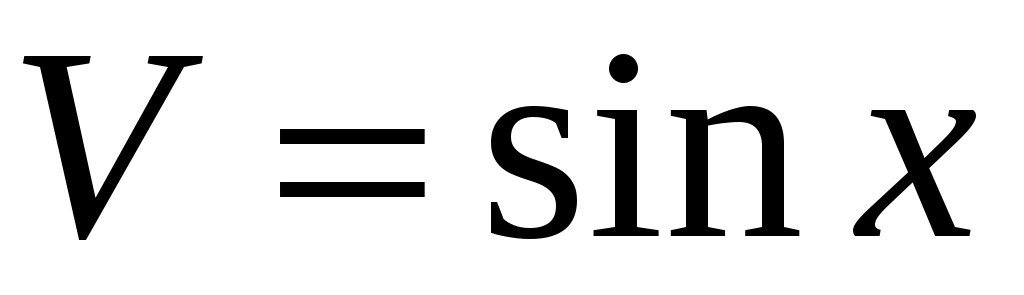 . Таким образом,
. Таким образом,
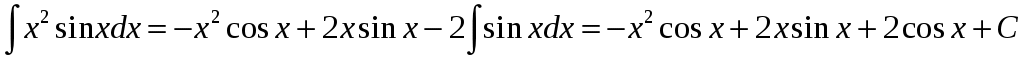 .
.
Проверим этот результат дифференцированием:
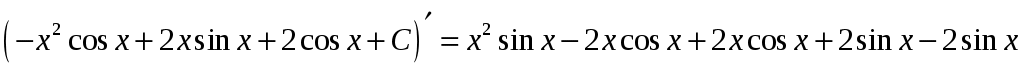 или
или 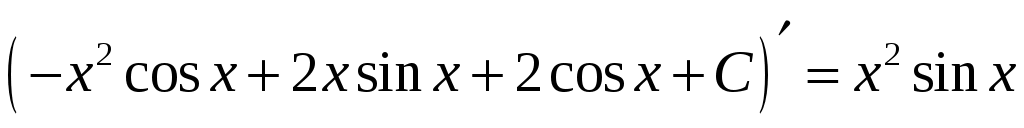 .
.
в)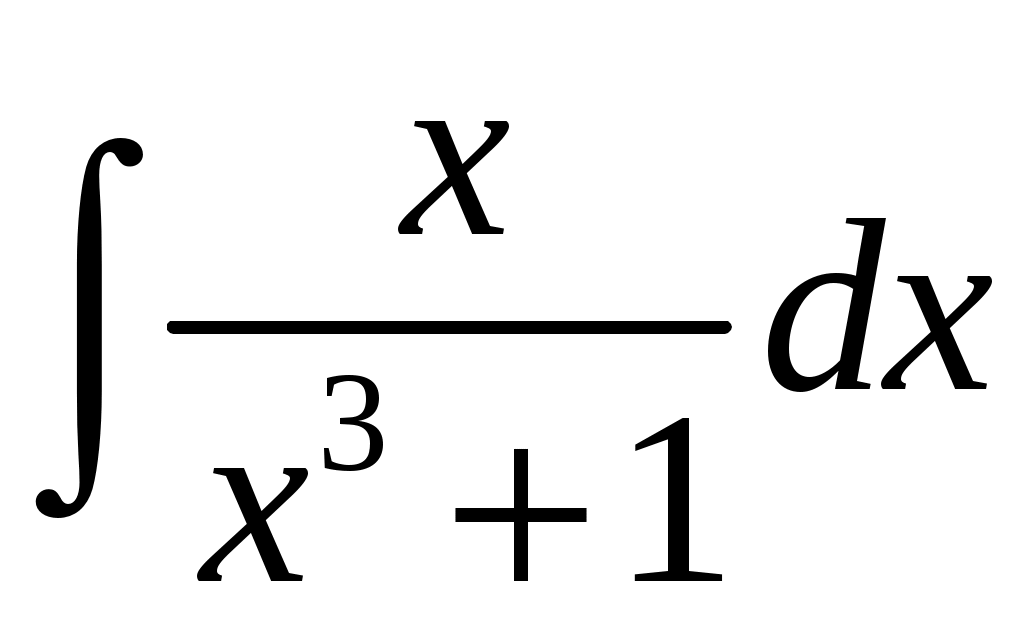 . Подынтегральная функция является правильной рациональной дробью, знаменатель которой можно разложить
. Подынтегральная функция является правильной рациональной дробью, знаменатель которой можно разложить 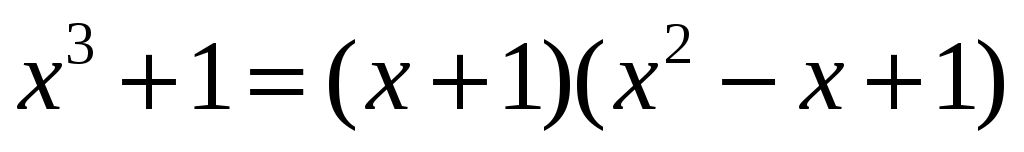 . Тогда подынтегральная функция раскладывается на сумму простейших дробей
. Тогда подынтегральная функция раскладывается на сумму простейших дробей 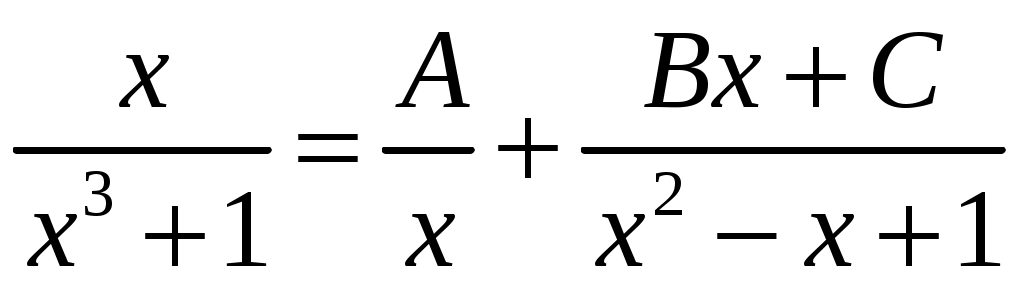 . Откуда, приравнивая числители, находим
. Откуда, приравнивая числители, находим 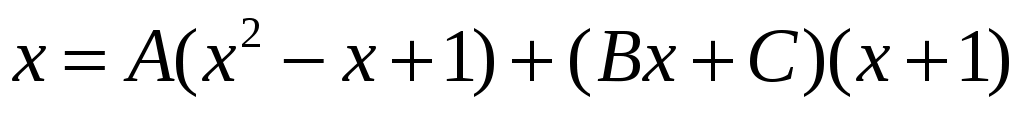 . Раскроем скобки в правой части и приведем подобные:
. Раскроем скобки в правой части и приведем подобные:
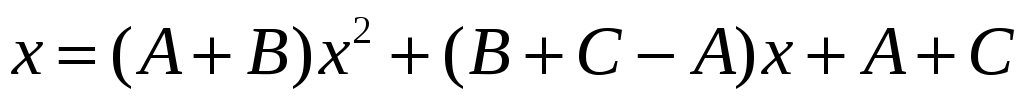 .
.
Приравнивая соответствующие коэффициенты при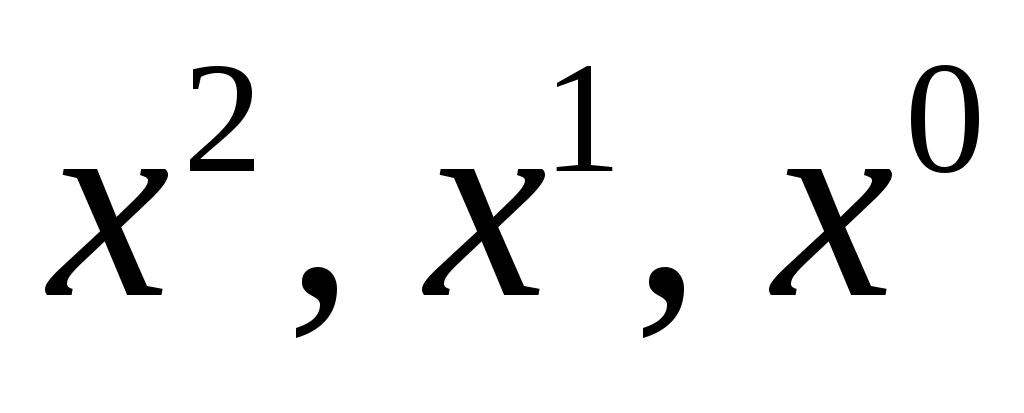 в левой и правой частях последнего равенства, получим систему из трех уравнений:
в левой и правой частях последнего равенства, получим систему из трех уравнений:
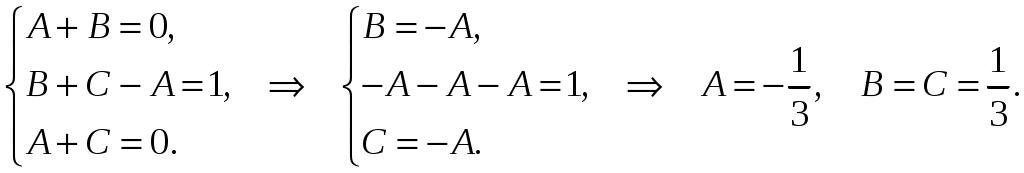
Тогда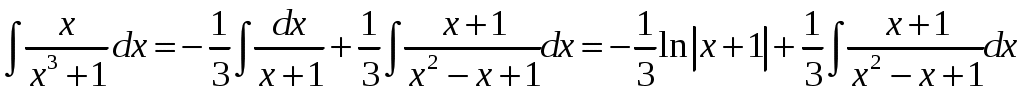 .
.
Вычислим отдельно последний интеграл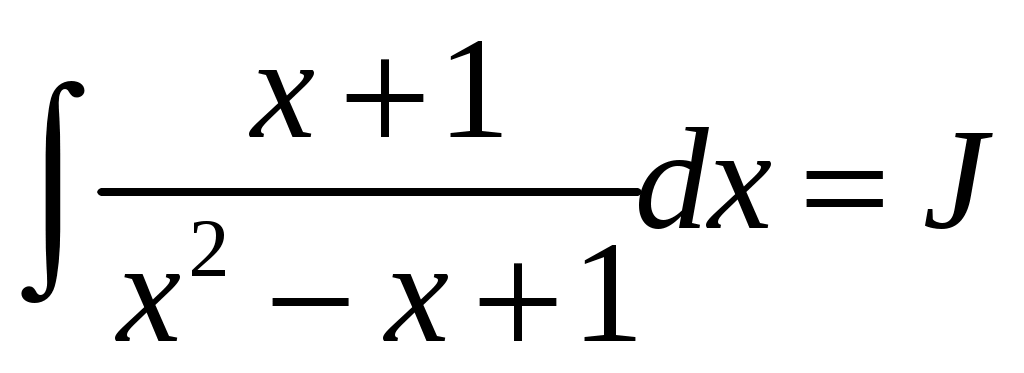 . Используя равенства
. Используя равенства 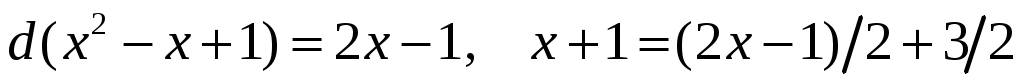 , получаем, что
, получаем, что 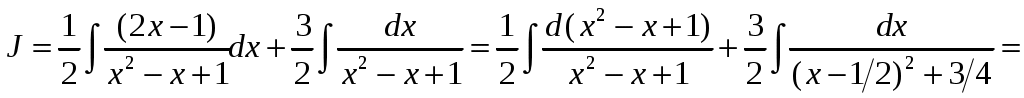
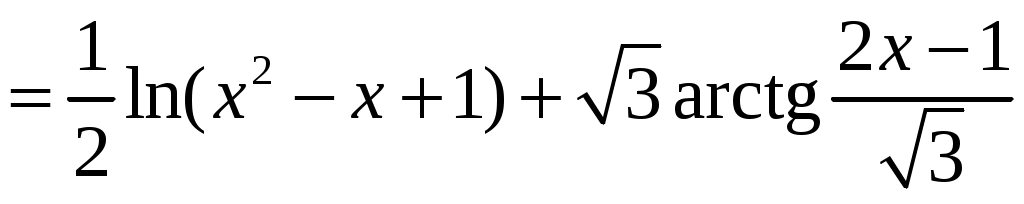 . Отсюда, окончательно, получаем интеграл
. Отсюда, окончательно, получаем интеграл 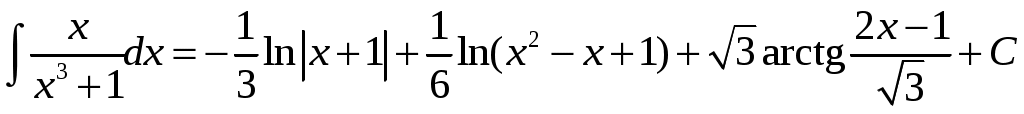 .
.
г)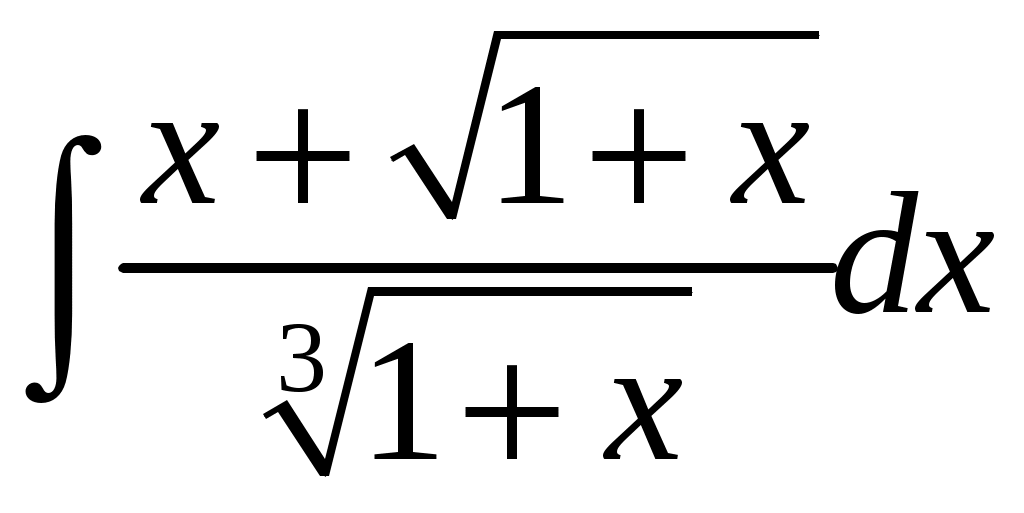
. Наименьшее общее кратное показателей корней равно 6, поэтому выполним подстановку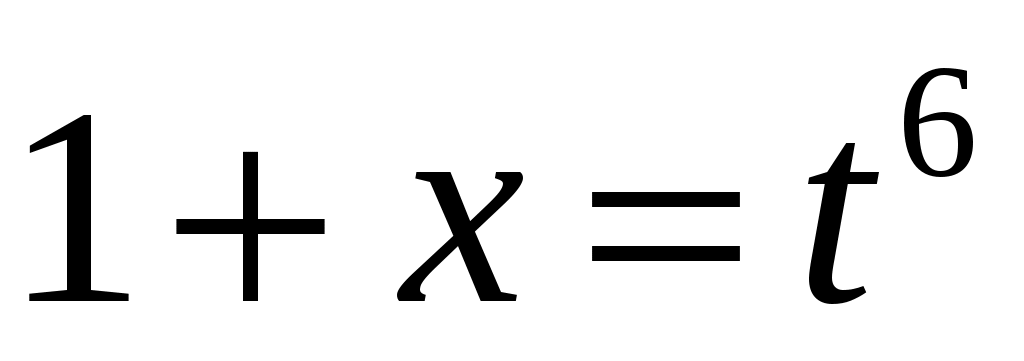 ,
,  , тогда
, тогда
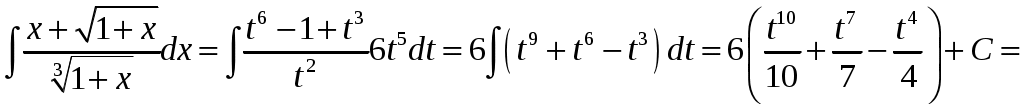
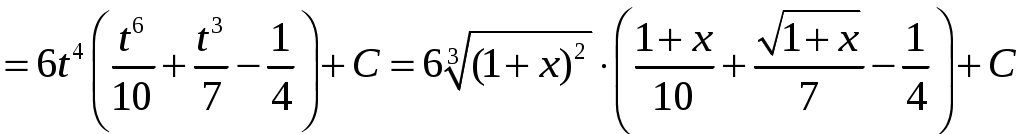 .
.
Задание № 2. Вычислить несобственный интеграл или установить его расходимость.
Пример.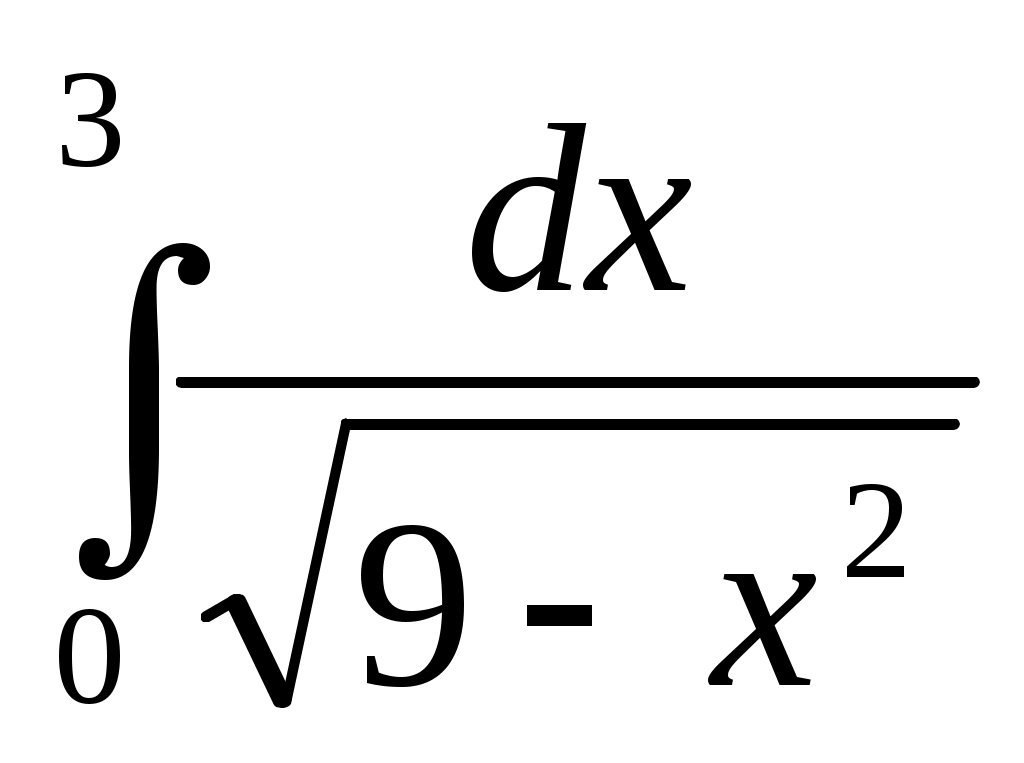 . Решение: Согласно формуле
. Решение: Согласно формуле 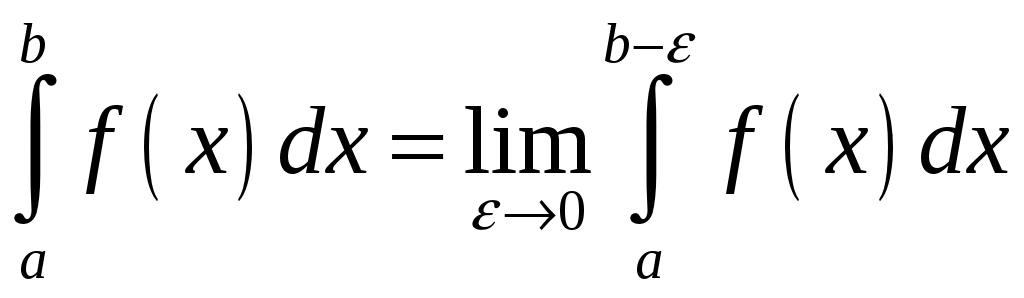 . Тогда имеем
. Тогда имеем
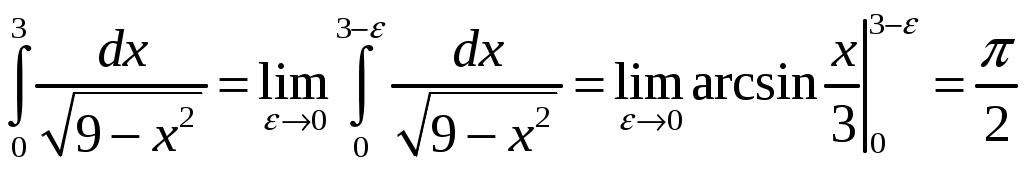 . Интеграл сходится.
. Интеграл сходится.
Задание № 3. Вычислить объем тела, образованного вращением вокруг оси Ох кривой L
Пример.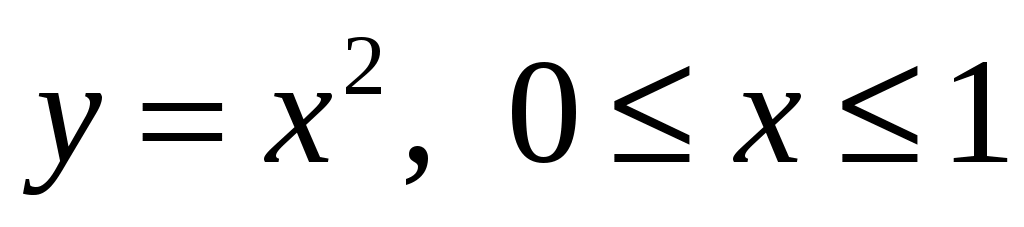 . Объём тела вращения находим по формуле:
. Объём тела вращения находим по формуле: 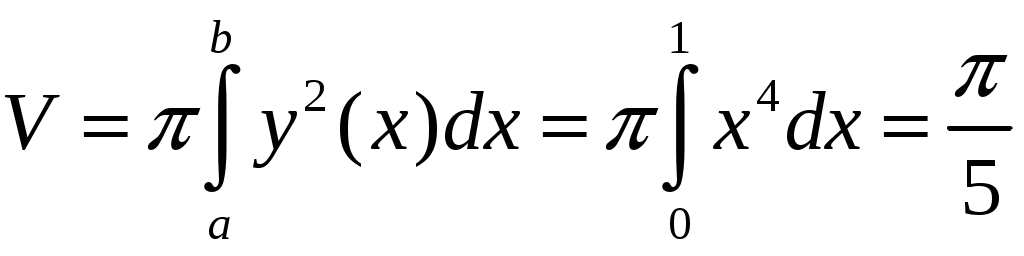 .
.
Задание № 4. Исследовать сходимость числового ряда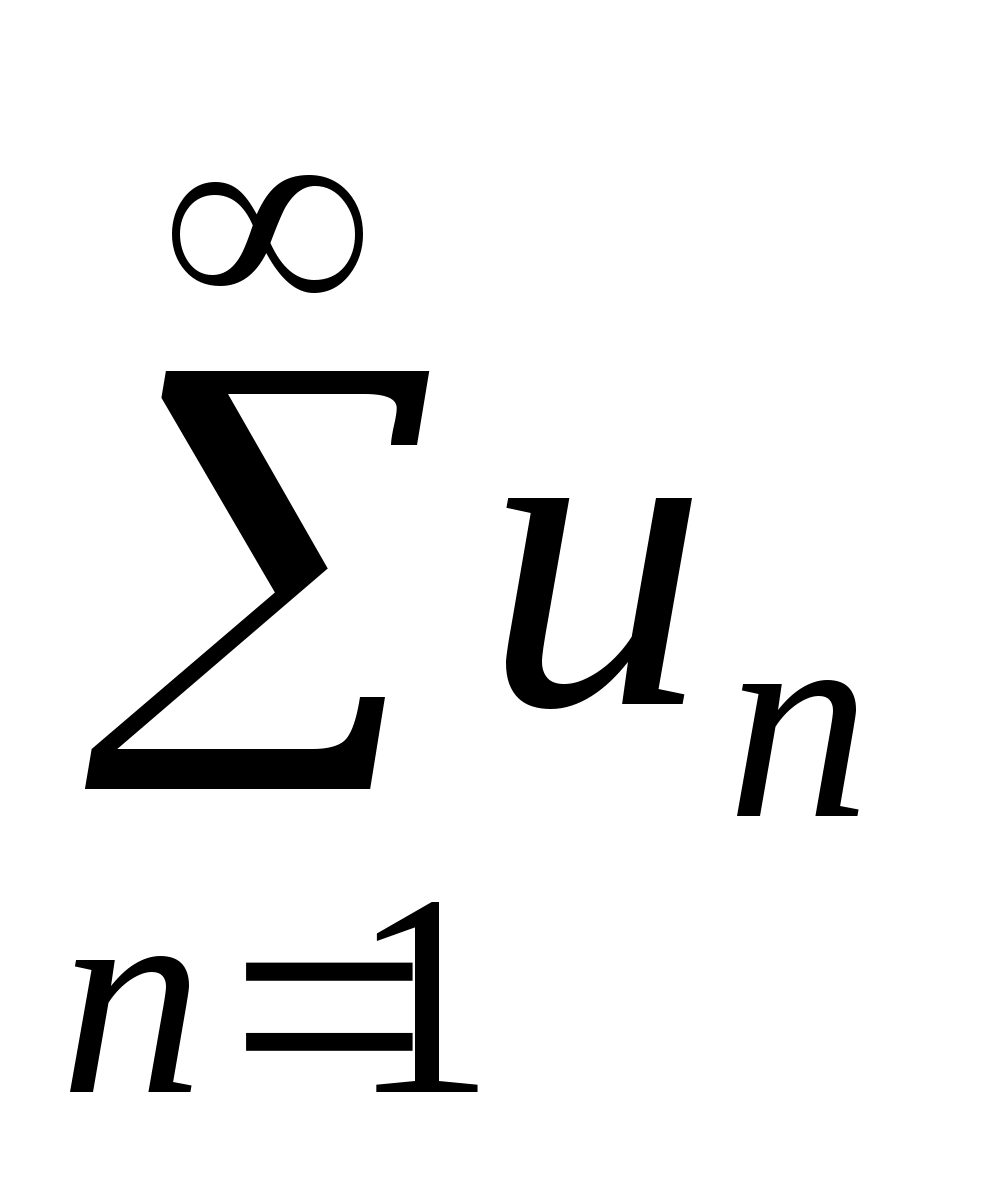 .
.
Пример 1.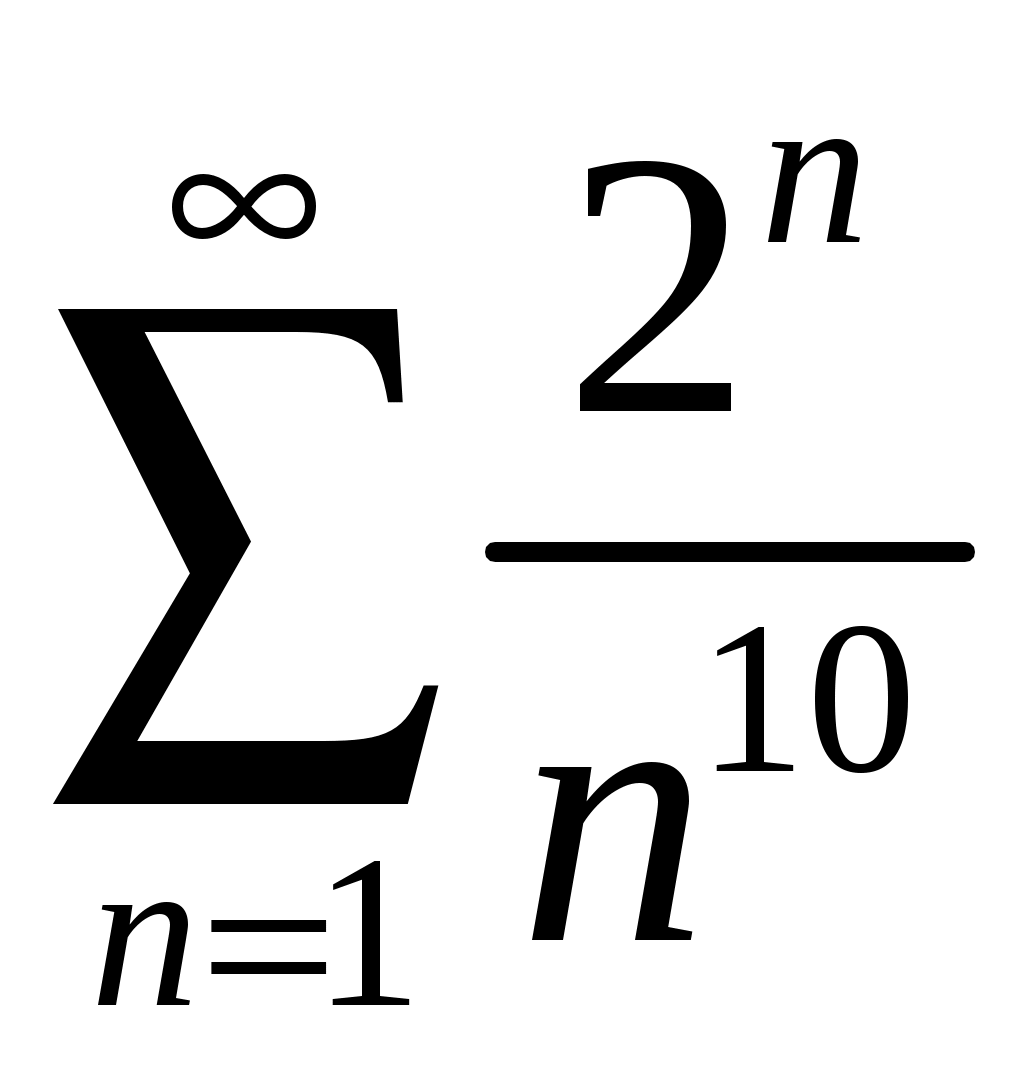 . Для этого ряда применим признак Даламбера:
. Для этого ряда применим признак Даламбера: 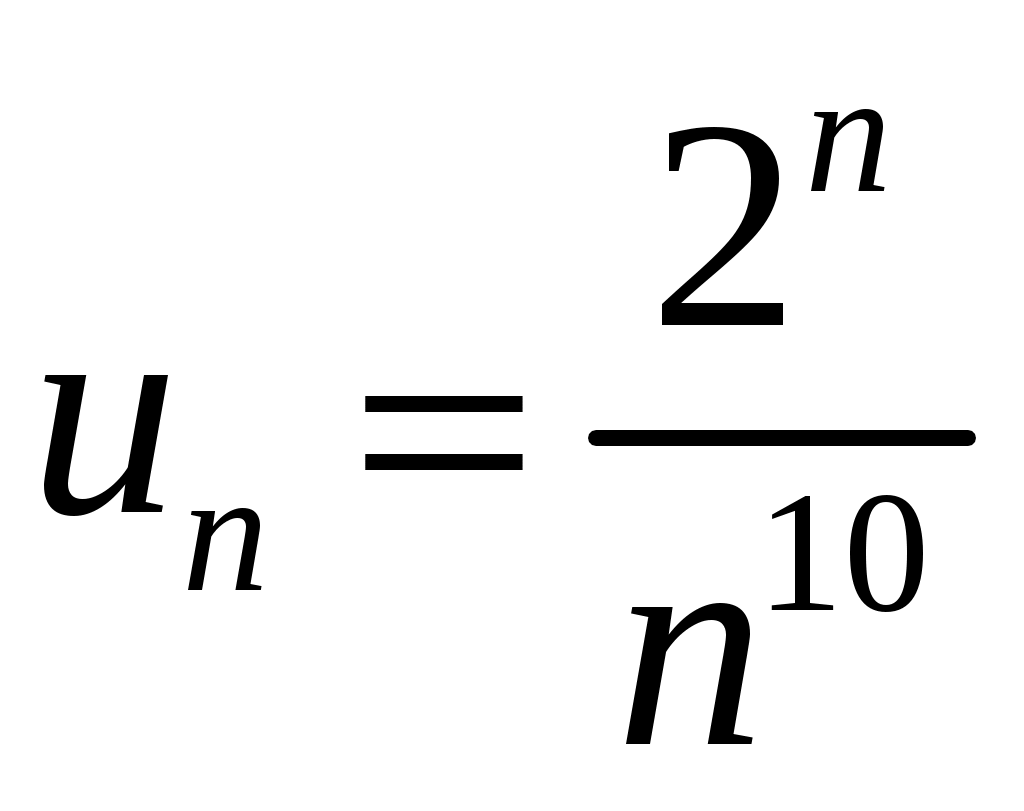 ,
, 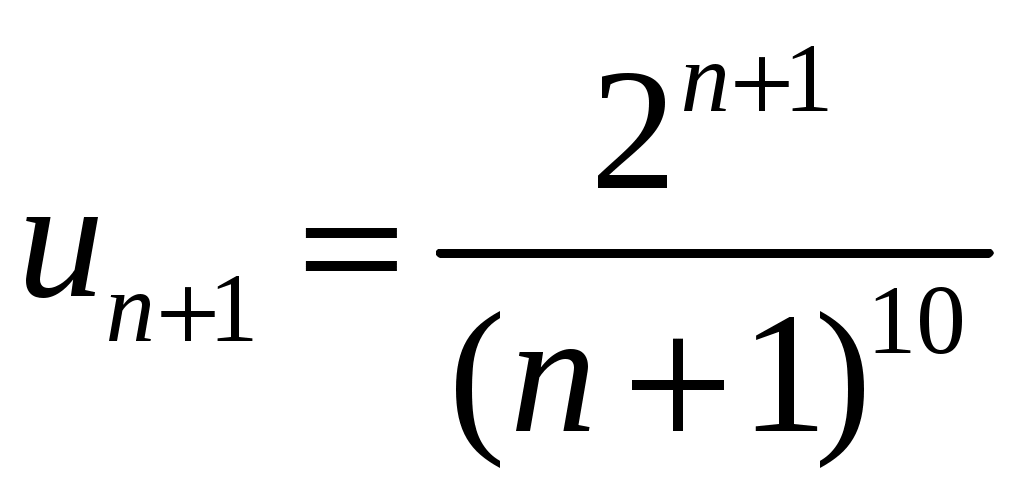 ,
, 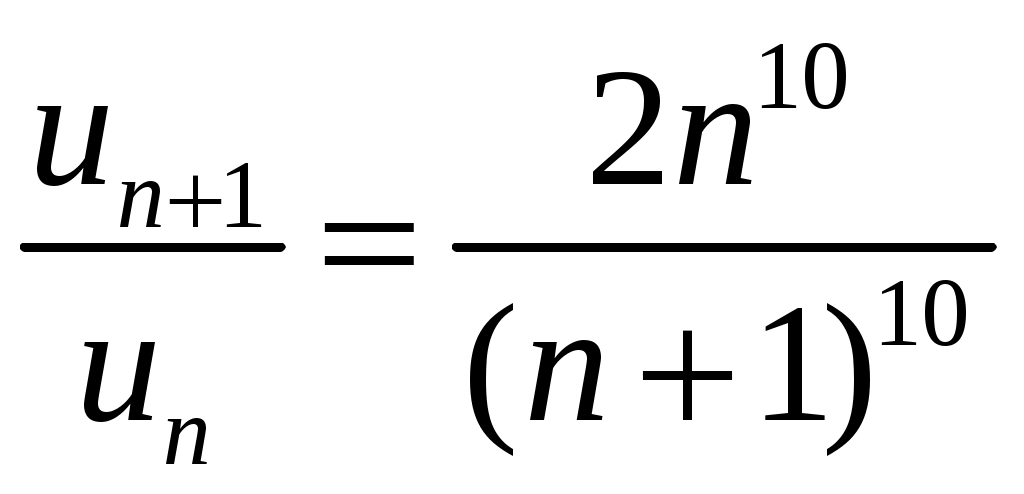 . Тогда
. Тогда 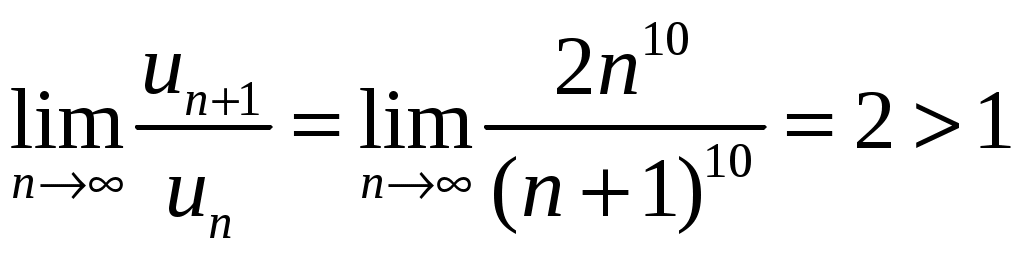 .
.
Тогда по признаку Даламбера ряд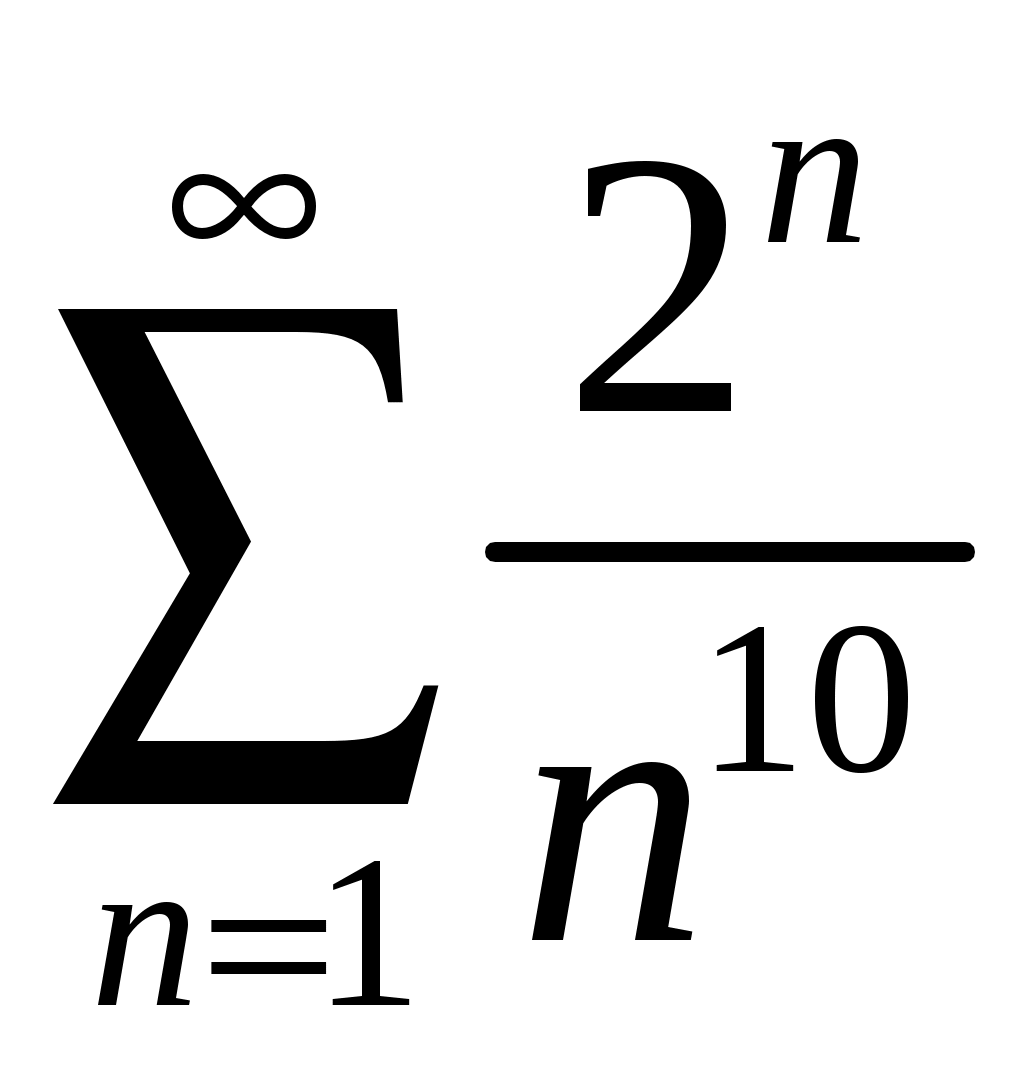 расходится.
расходится.
Пример 2.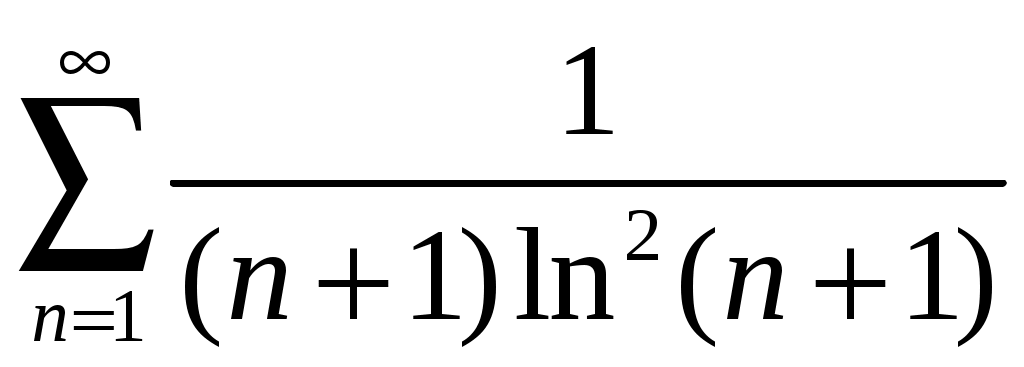 . Применим интегральный признак Маклорена Коши, составив функцию
. Применим интегральный признак Маклорена Коши, составив функцию 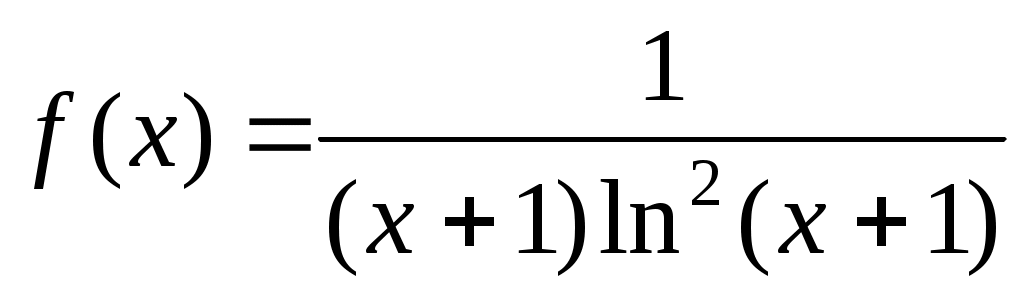 . Так как на интервале
. Так как на интервале 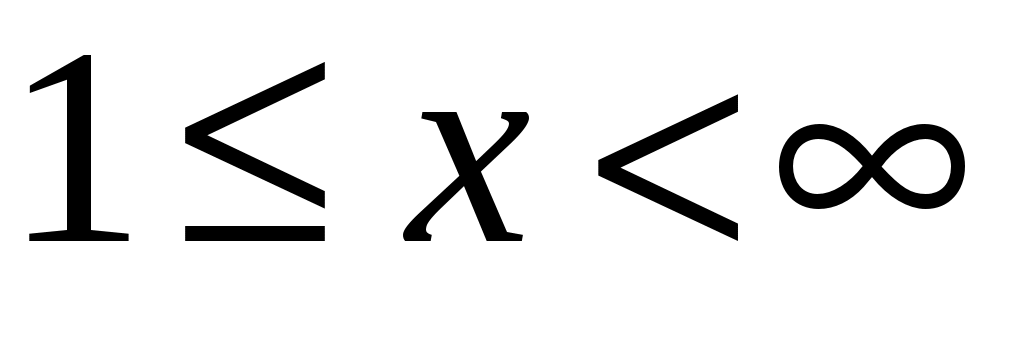 эта функция
эта функция 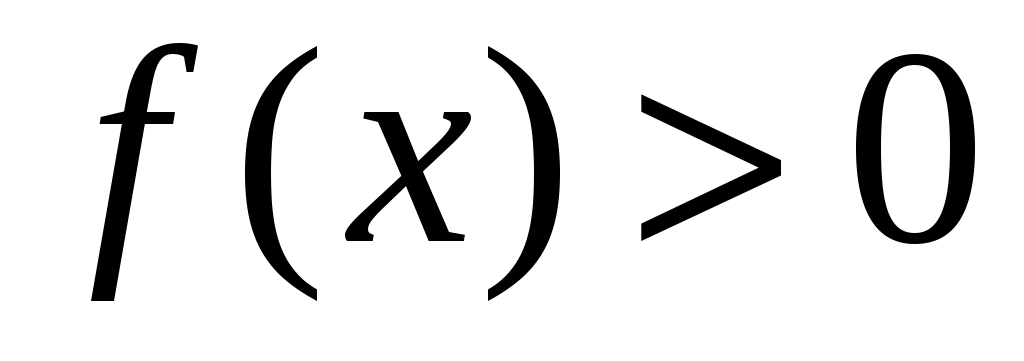 и с ростом
и с ростом 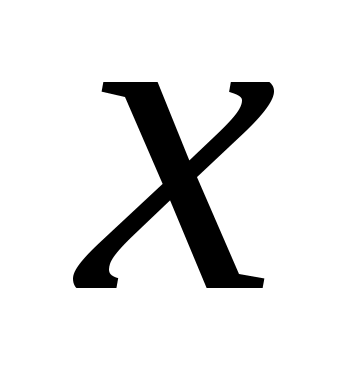 монотонно убывает, то ряд сходится или расходится одновременно с несобственным интегралом:
монотонно убывает, то ряд сходится или расходится одновременно с несобственным интегралом: 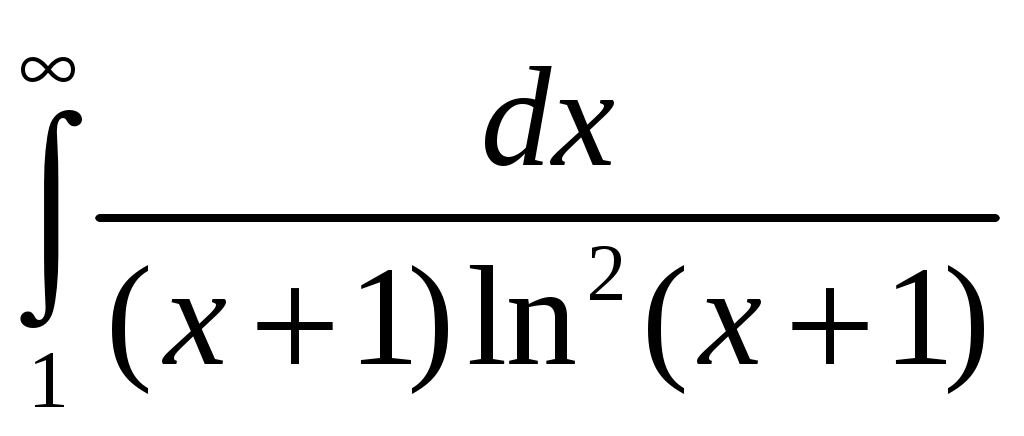
. Данный интеграл сходится, так как
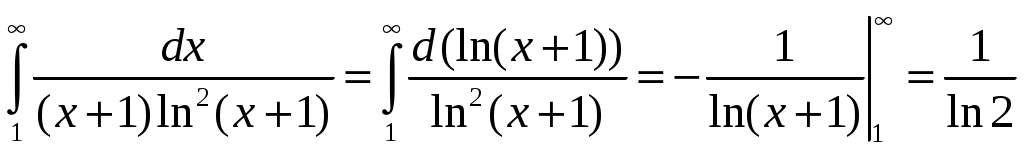 ,
,
поэтому сходится и данный ряд.
Задание № 5. Найти интервал сходимости степенного ряда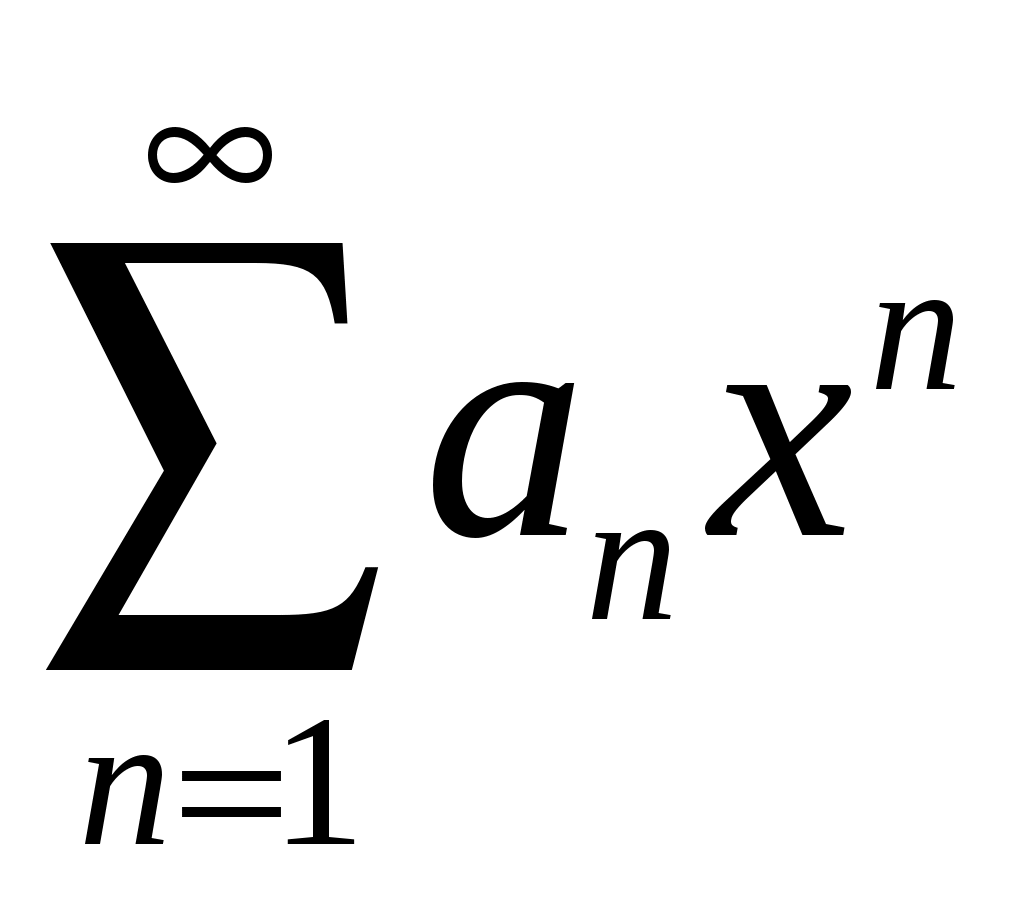 .
.
Пример.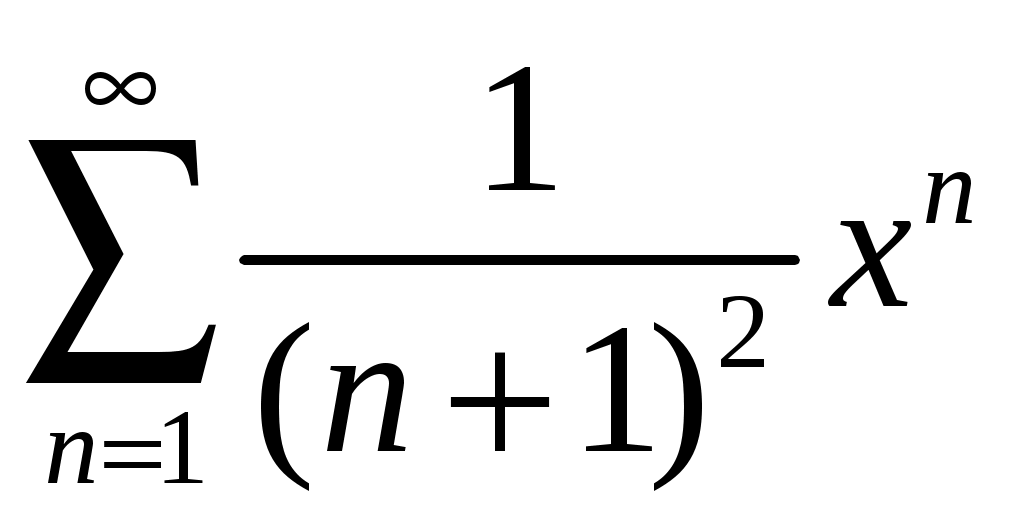 . Коэффициенты ряда:
. Коэффициенты ряда: 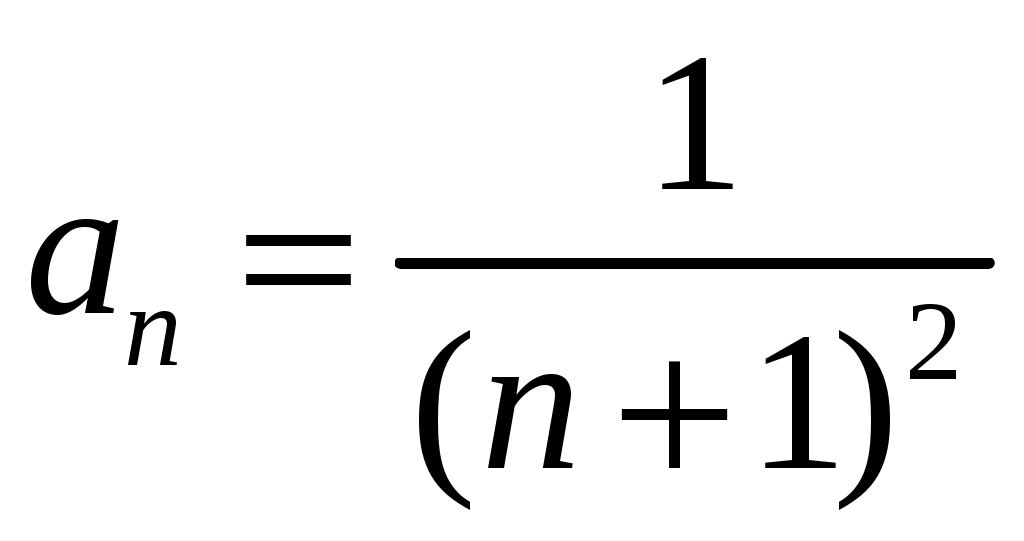 ,
, 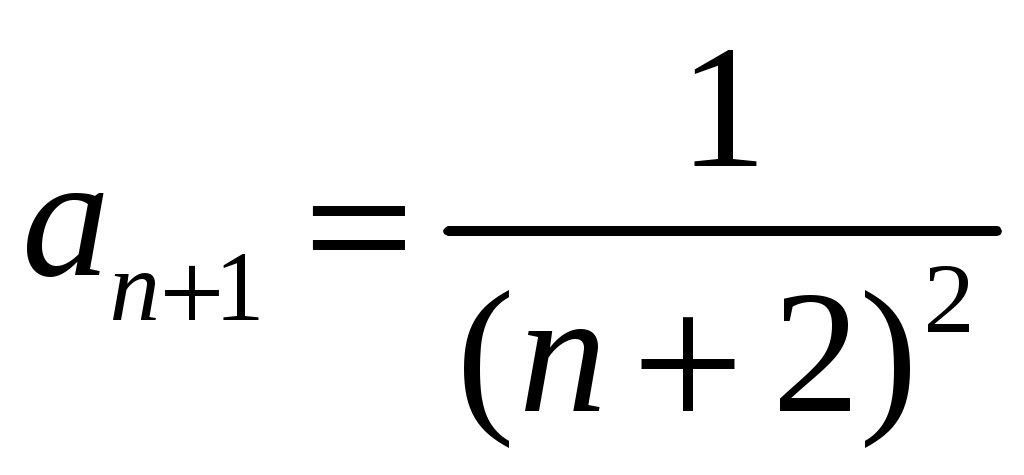 . Подставим их в формулу для радиуса сходимости степенного ряда:
. Подставим их в формулу для радиуса сходимости степенного ряда:
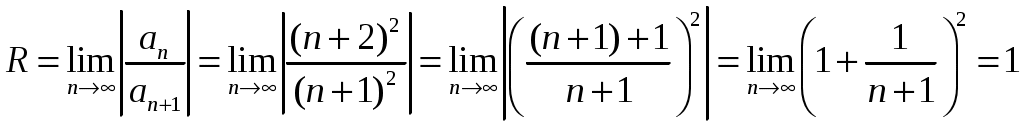 .
.
Следовательно, ряд сходится для значений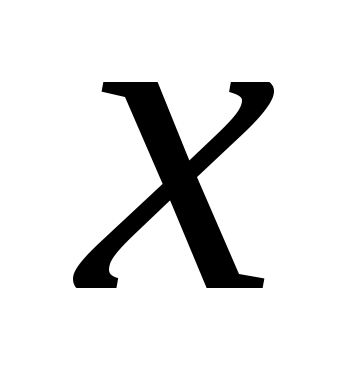 , удовлетворяющих неравенству
, удовлетворяющих неравенству 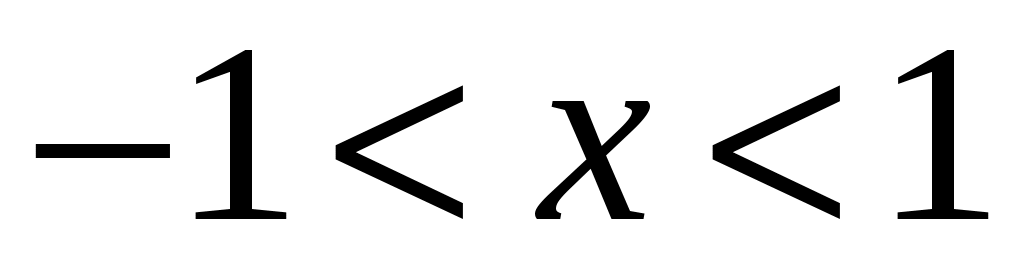 . Исследуем сходимость ряда на концах промежутка. Если
. Исследуем сходимость ряда на концах промежутка. Если 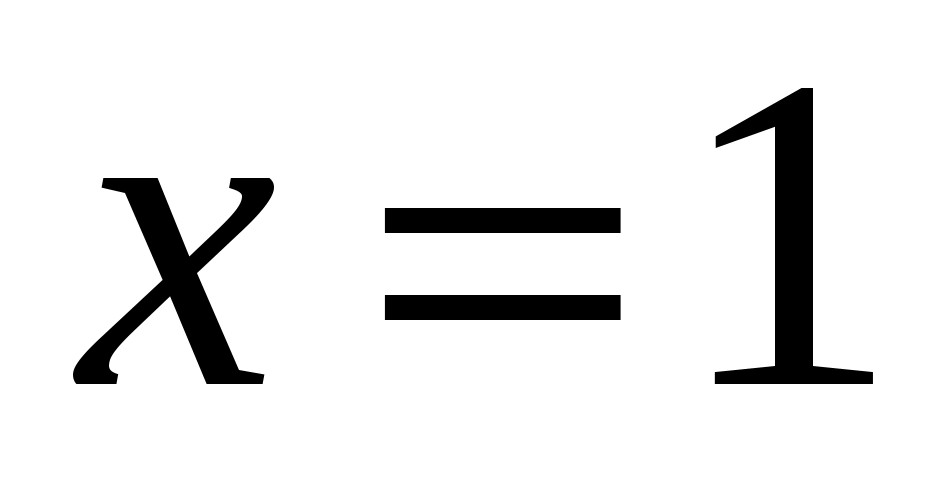 , то получим обобщенный гармонический ряд
, то получим обобщенный гармонический ряд 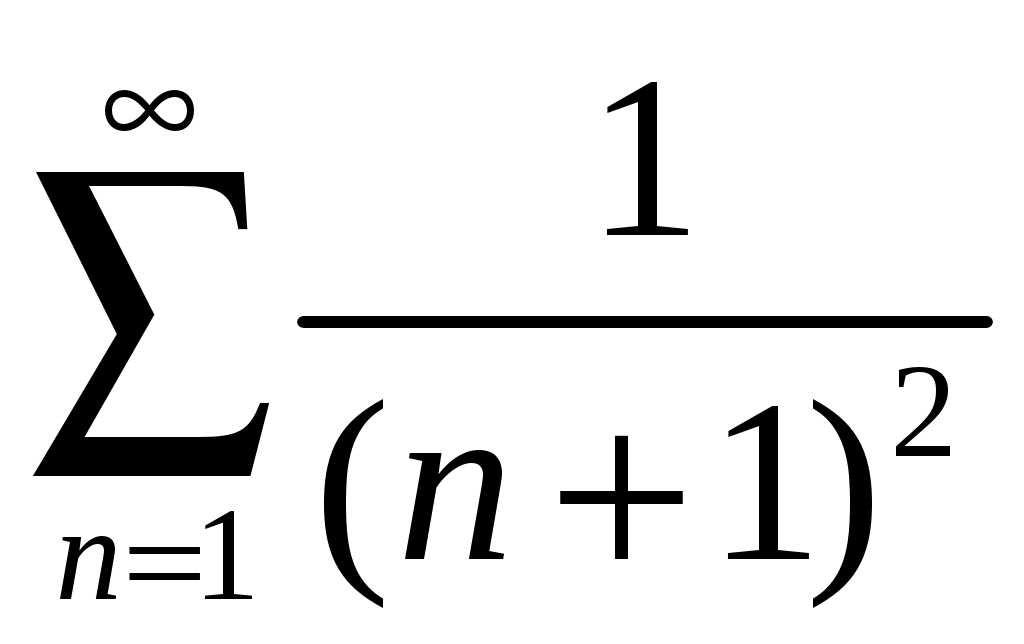 , который сходится, так как
, который сходится, так как 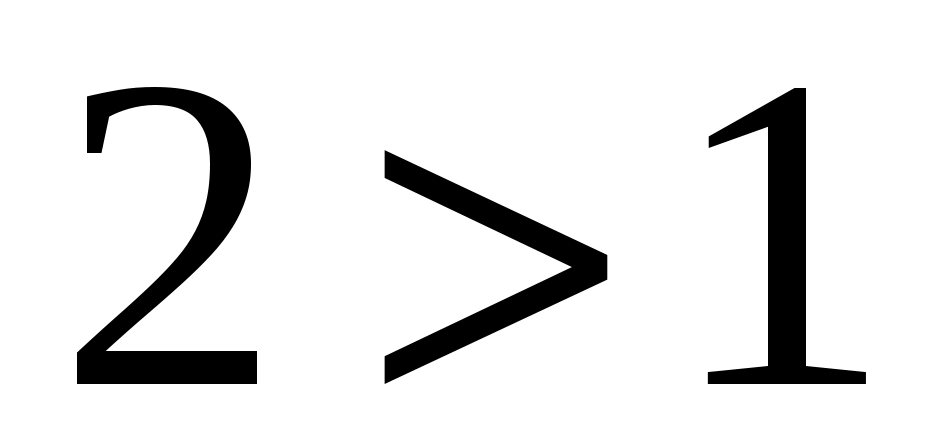 . Если
. Если 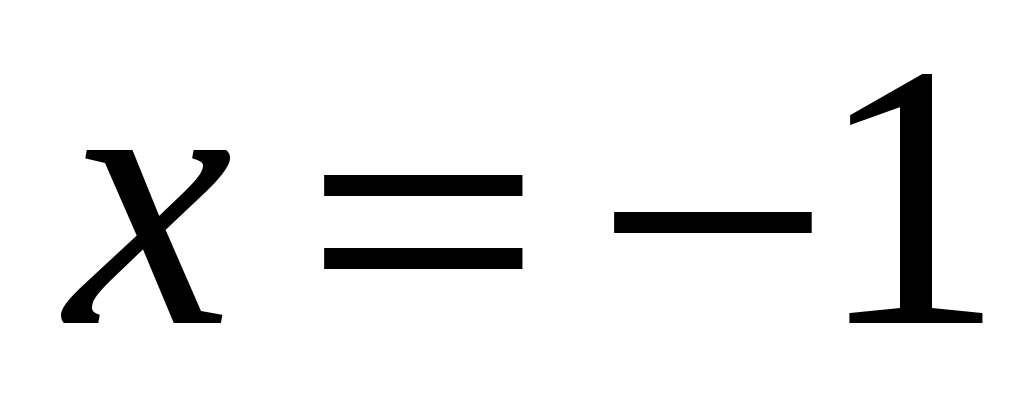 , то получим знакопеременный ряд
, то получим знакопеременный ряд 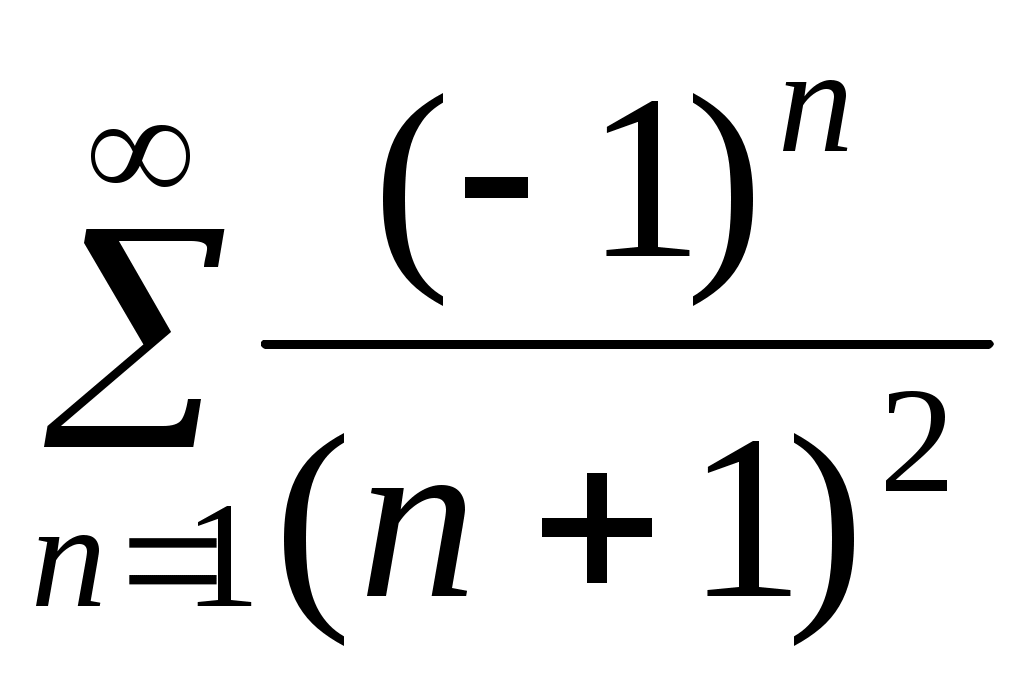 , который сходится, так как удовлетворяет условиям признака Лейбница.
, который сходится, так как удовлетворяет условиям признака Лейбница.
Задание №6. Найти частные производные 1-го порядка.
Пример.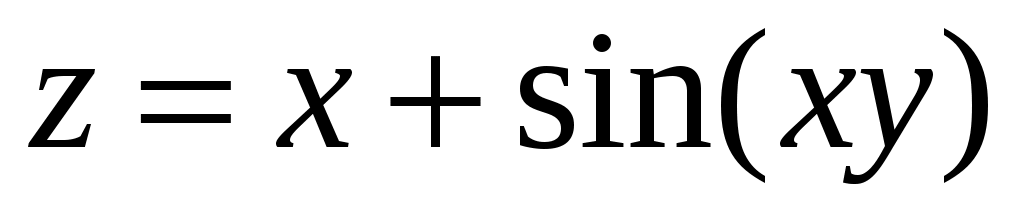 . Находим частые производные
. Находим частые производные
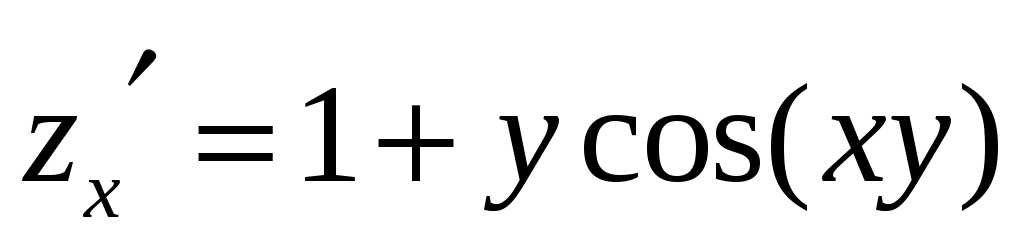 ,
, 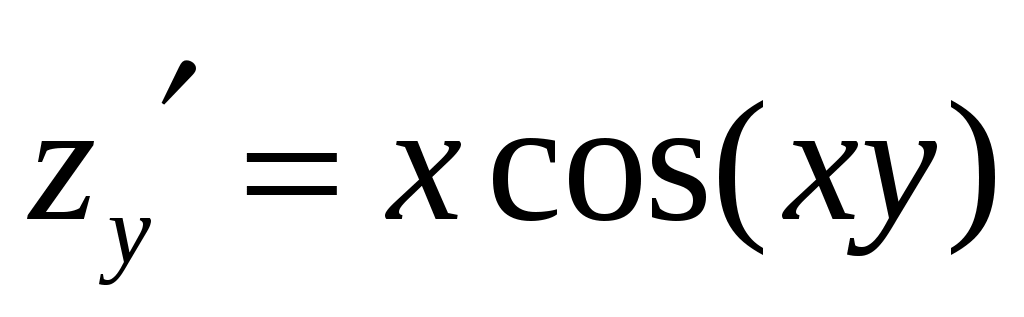 .
.
Задания №7 и № 8. Решить задачу по теории вероятности.
Пример 1. Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению и 20 задач по интегральному исчислению. Для сдачи зачета студент должен решить первый же доставшийся наугад билет из трех задач по одной задаче на каждую тему. Какова вероятность для студента сдать зачет,
если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение. Число билетов, которое может составить преподаватель, равно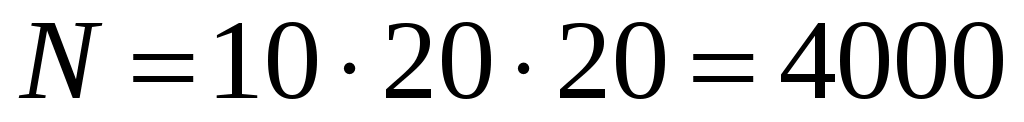 . Число билетов, которое знает студент, равно
. Число билетов, которое знает студент, равно 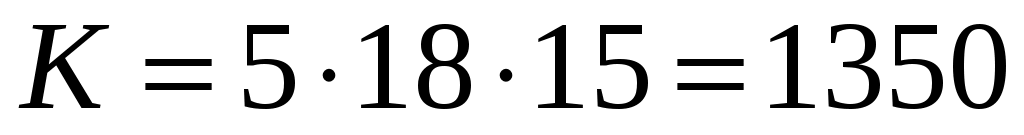 . Считая, что студенту билет достается случайным образом и что это равновероятные события, получаем вероятность сдачи зачета:
. Считая, что студенту билет достается случайным образом и что это равновероятные события, получаем вероятность сдачи зачета:
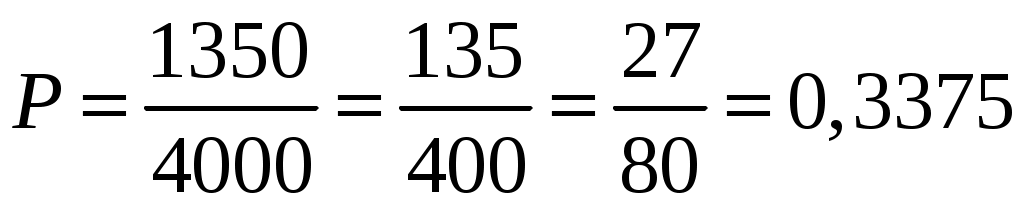 .
.
Пример 2. Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению, 20 по интегральному исчислению. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение № 1. Студент знает 38 задач из пятидесяти, поэтому вероятность сдать зачет равна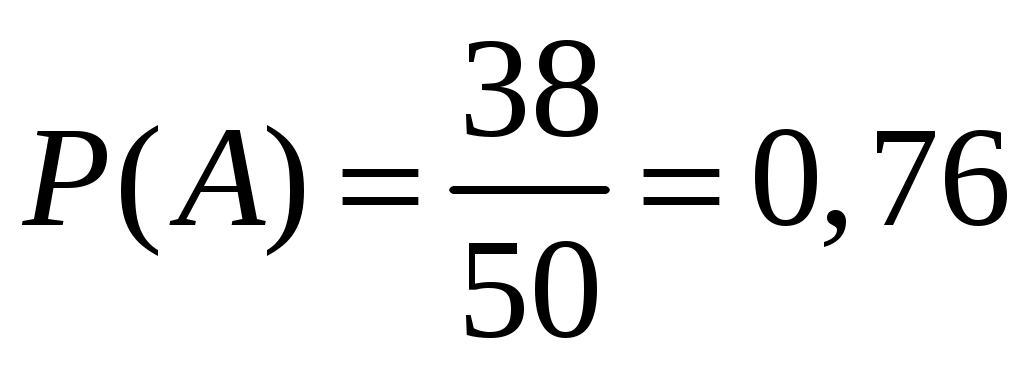 .
.
Решение № 2. Вероятность получить задачу по пределам (событие ) равна
) равна 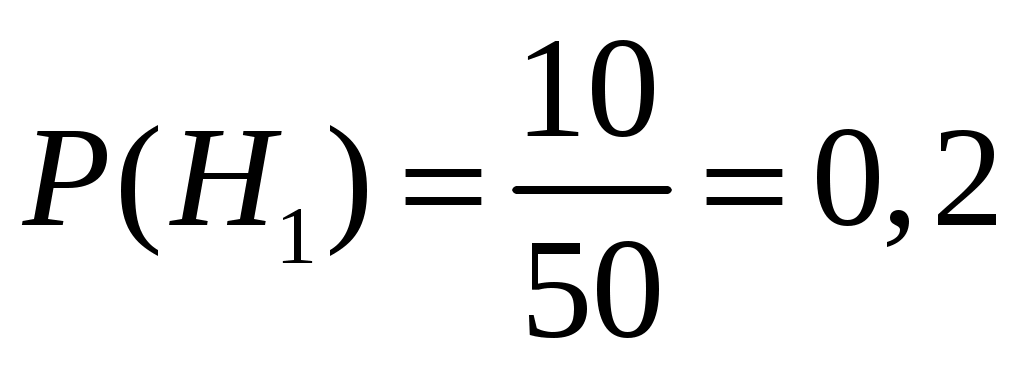 , вероятность получить задачу по дифференциальному исчислению (событие
, вероятность получить задачу по дифференциальному исчислению (событие 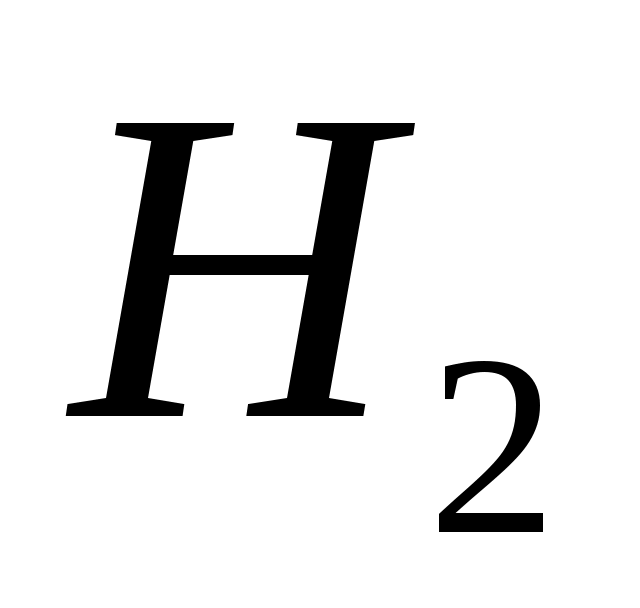 )равна
)равна 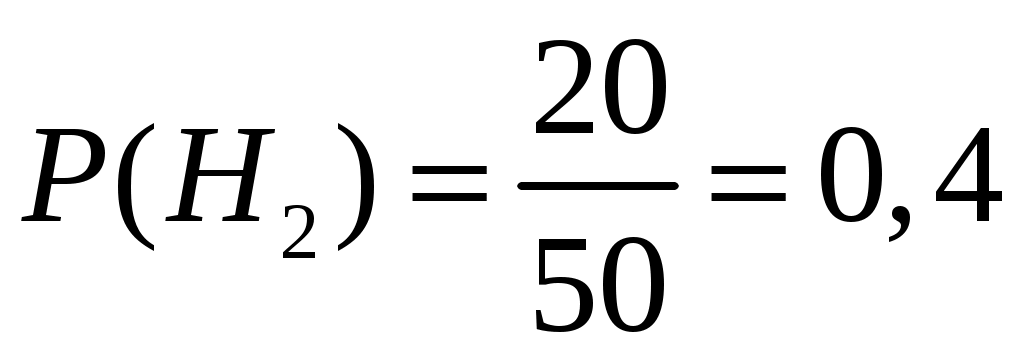 =0,4, вероятность получить задачу по интегральному исчислению (событие
=0,4, вероятность получить задачу по интегральному исчислению (событие 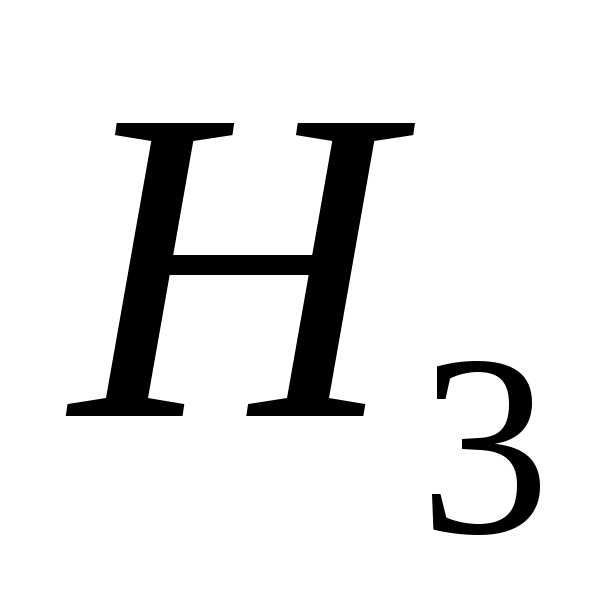 ) равна
) равна 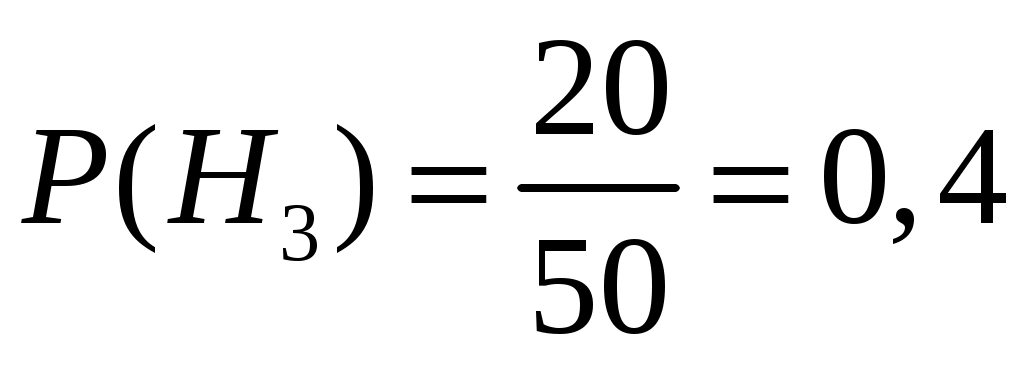 . Если событие
. Если событие 
Проверим этот результат дифференцированием:
в)
Приравнивая соответствующие коэффициенты при
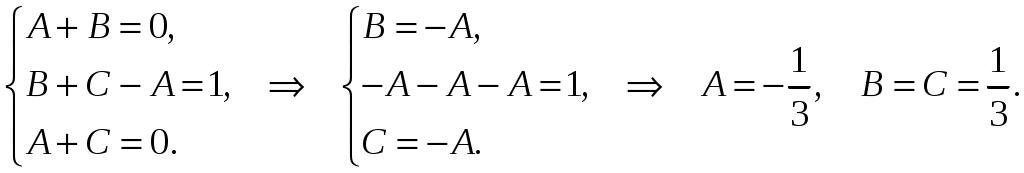
Тогда
Вычислим отдельно последний интеграл
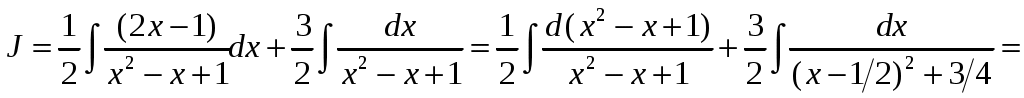
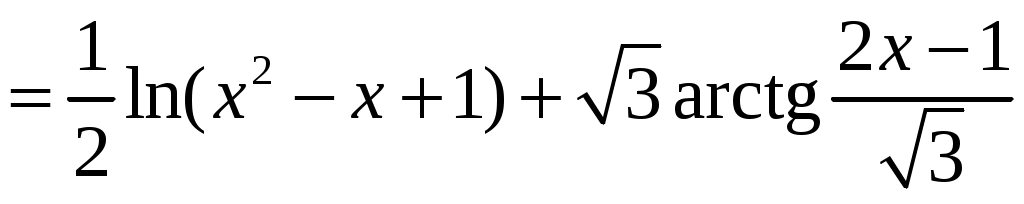 . Отсюда, окончательно, получаем интеграл
. Отсюда, окончательно, получаем интеграл 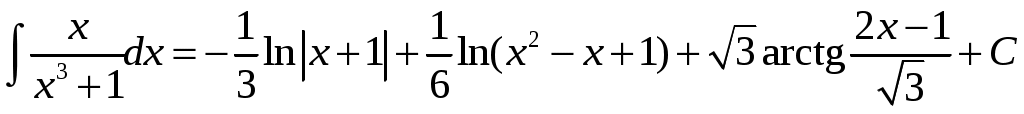 .
.г)
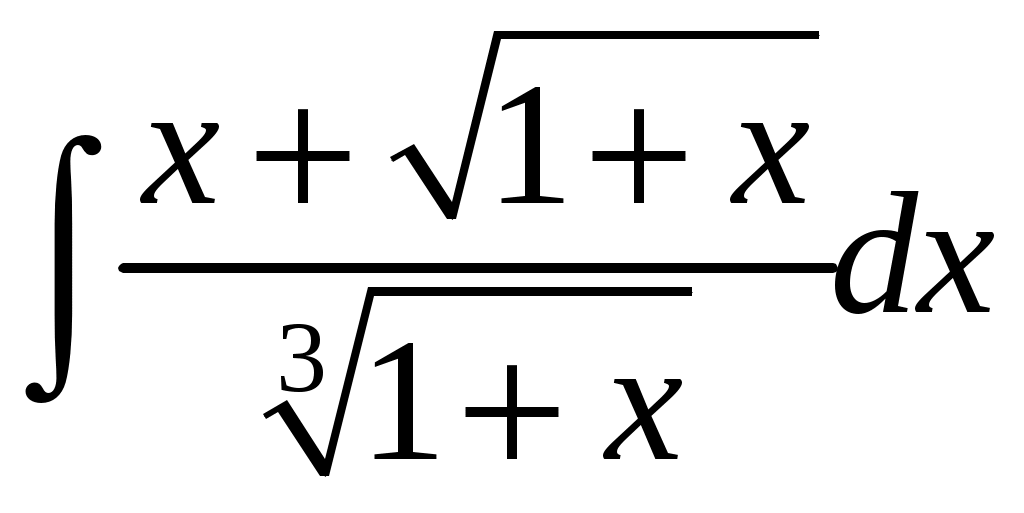
. Наименьшее общее кратное показателей корней равно 6, поэтому выполним подстановку
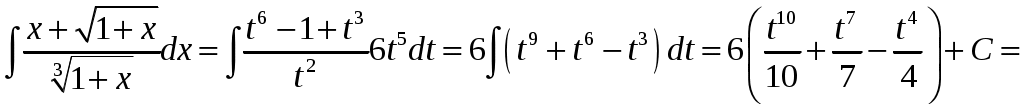
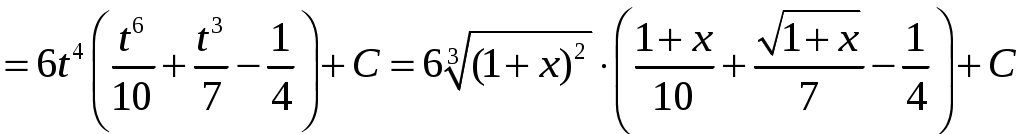 .
.Задание № 2. Вычислить несобственный интеграл или установить его расходимость.
Пример.
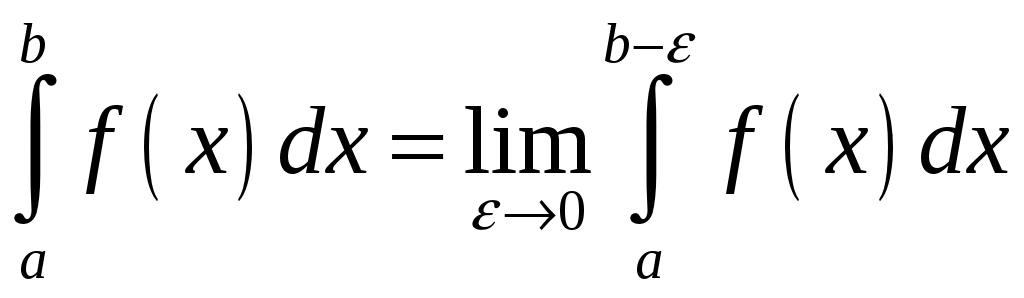 . Тогда имеем
. Тогда имеем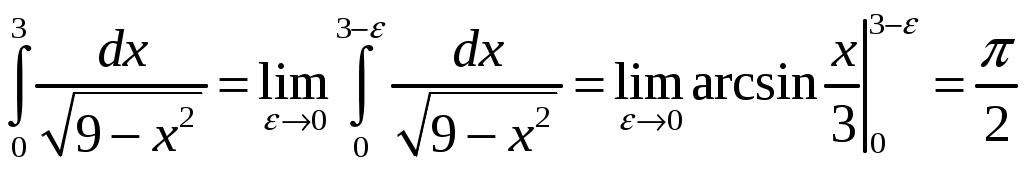 . Интеграл сходится.
. Интеграл сходится.Задание № 3. Вычислить объем тела, образованного вращением вокруг оси Ох кривой L
Пример.
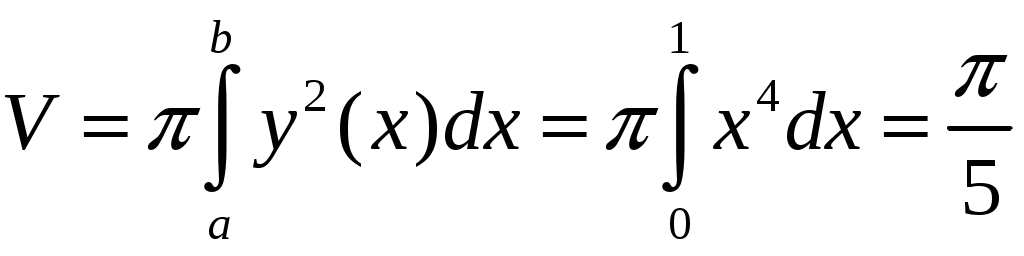 .
.Задание № 4. Исследовать сходимость числового ряда
Пример 1.
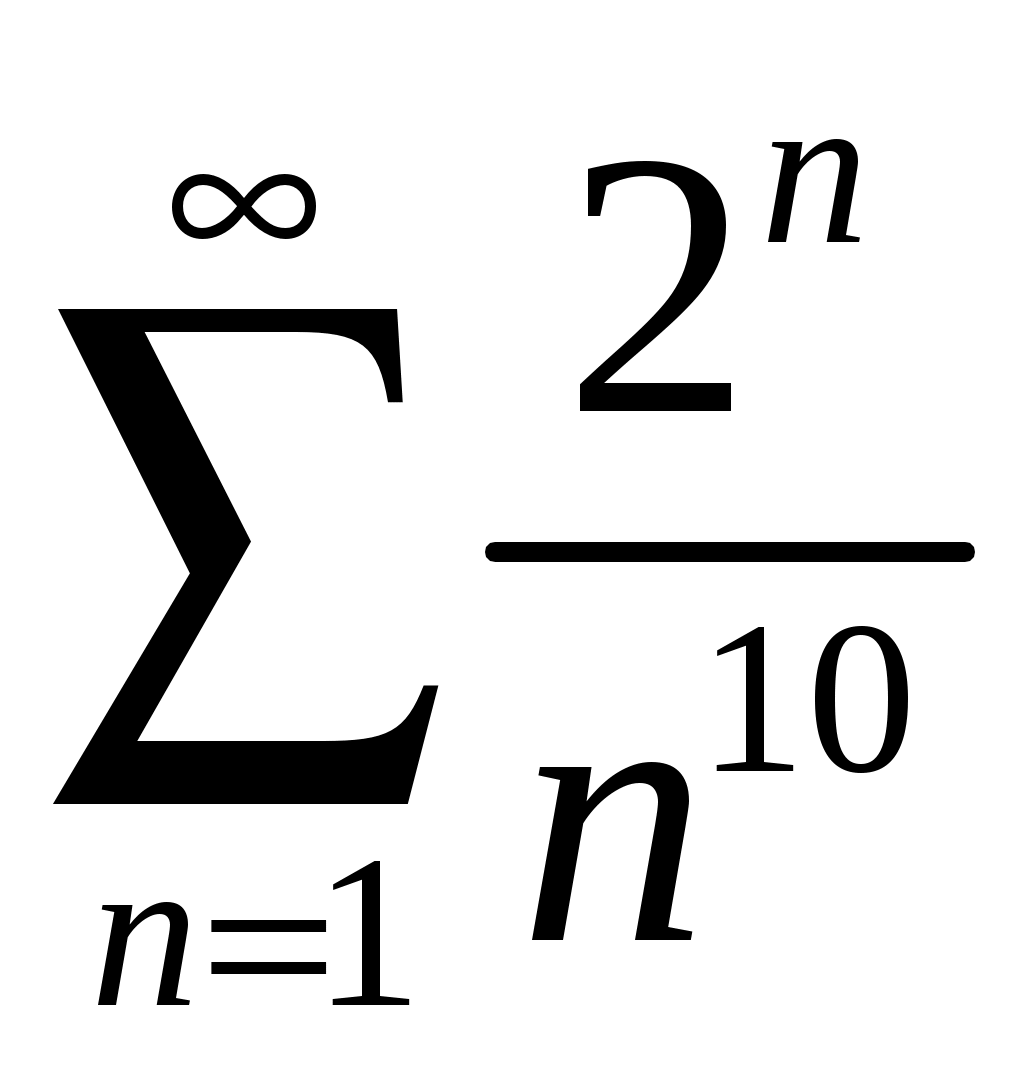 . Для этого ряда применим признак Даламбера:
. Для этого ряда применим признак Даламбера: 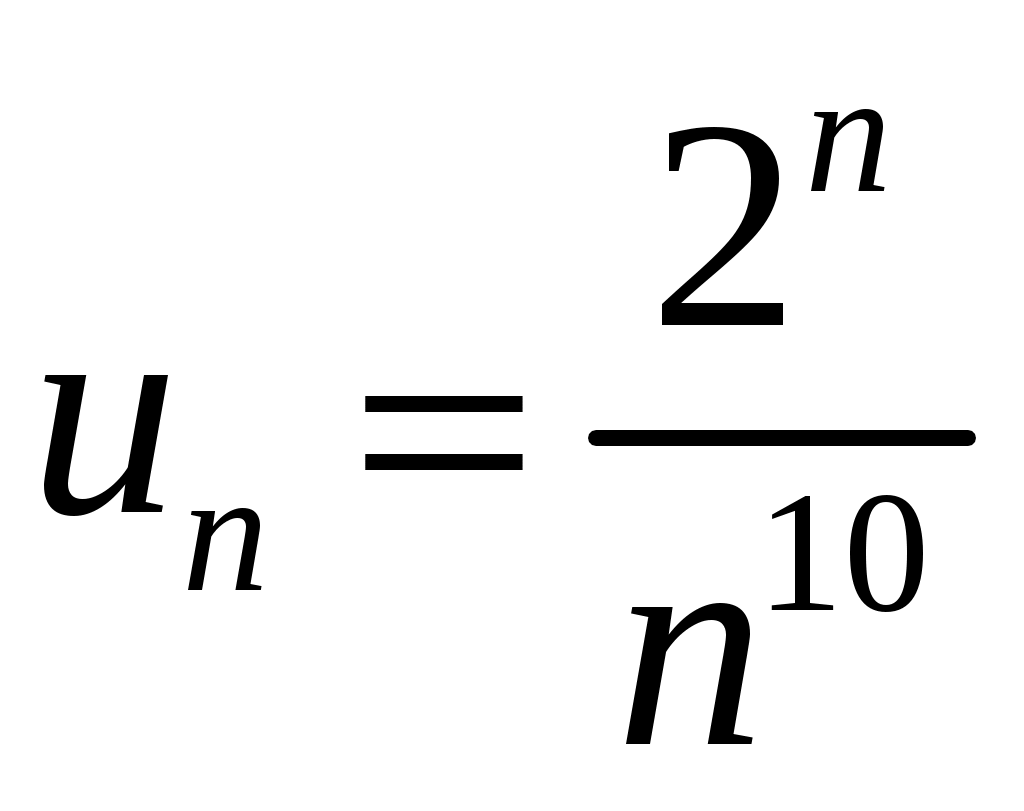 ,
, 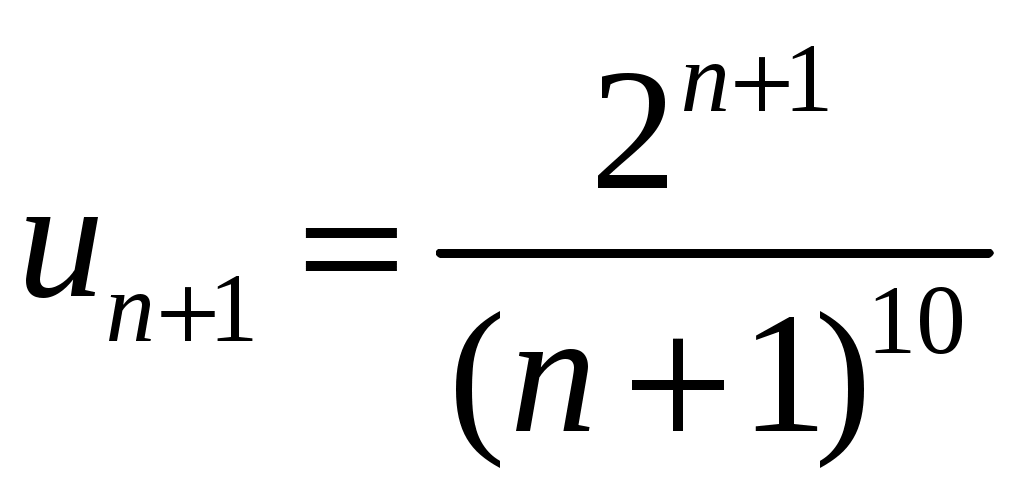 ,
, 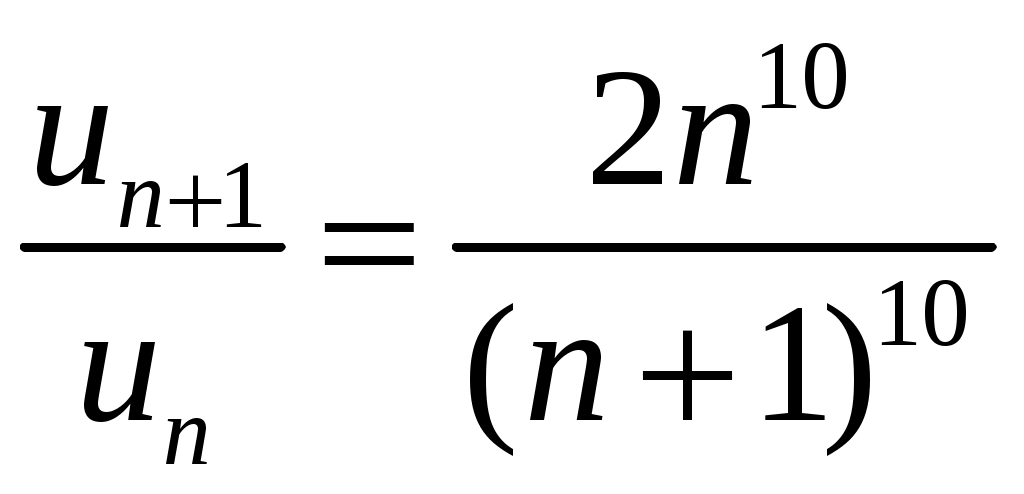 . Тогда
. Тогда 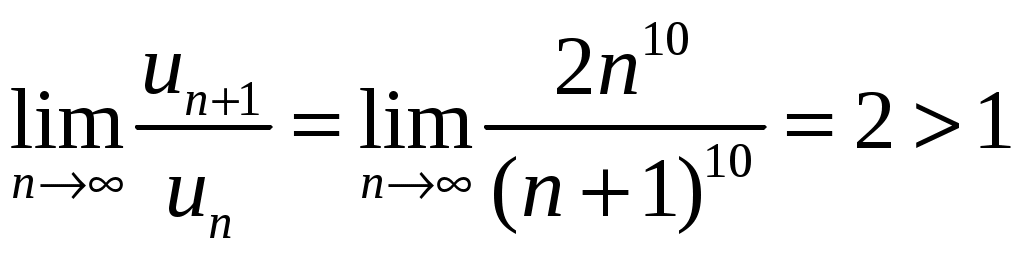 .
.Тогда по признаку Даламбера ряд
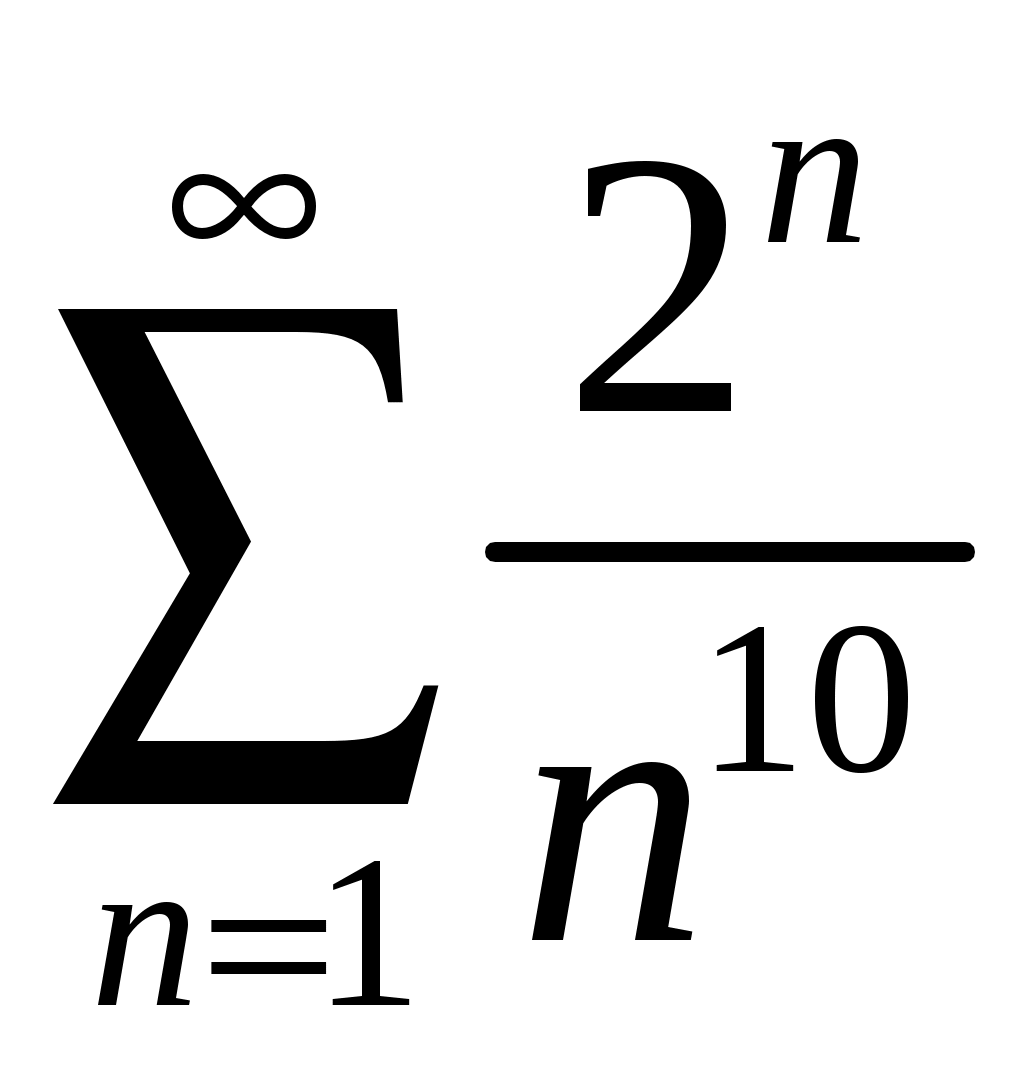 расходится.
расходится.Пример 2.
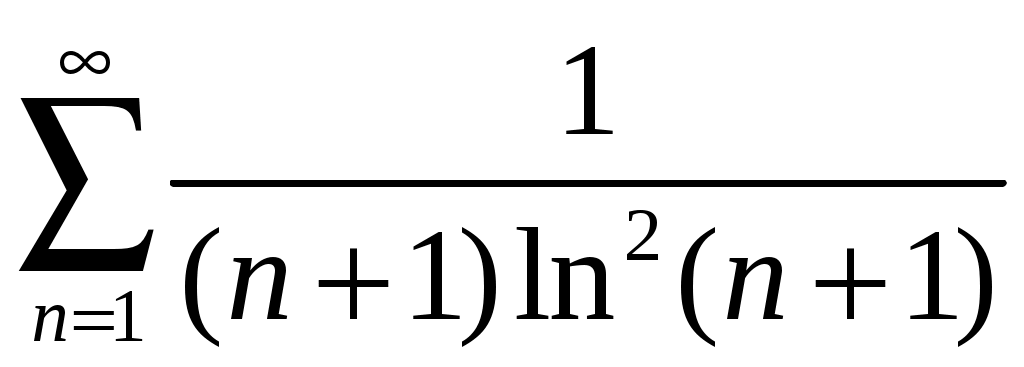 . Применим интегральный признак Маклорена Коши, составив функцию
. Применим интегральный признак Маклорена Коши, составив функцию 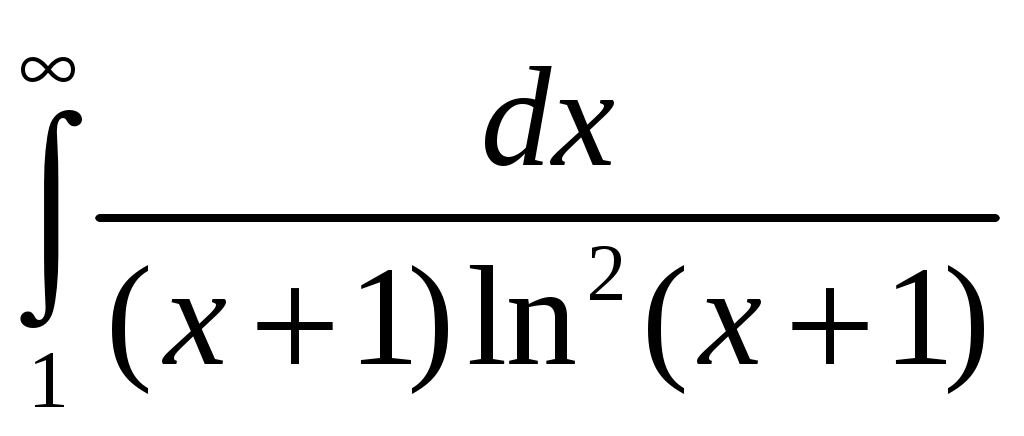
. Данный интеграл сходится, так как
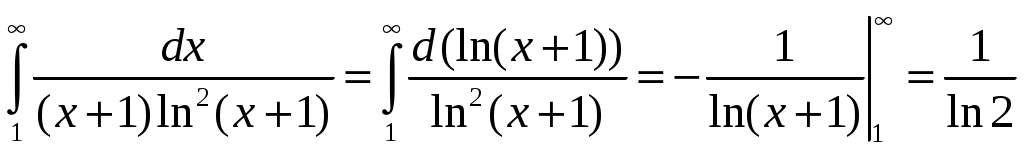 ,
,поэтому сходится и данный ряд.
Задание № 5. Найти интервал сходимости степенного ряда
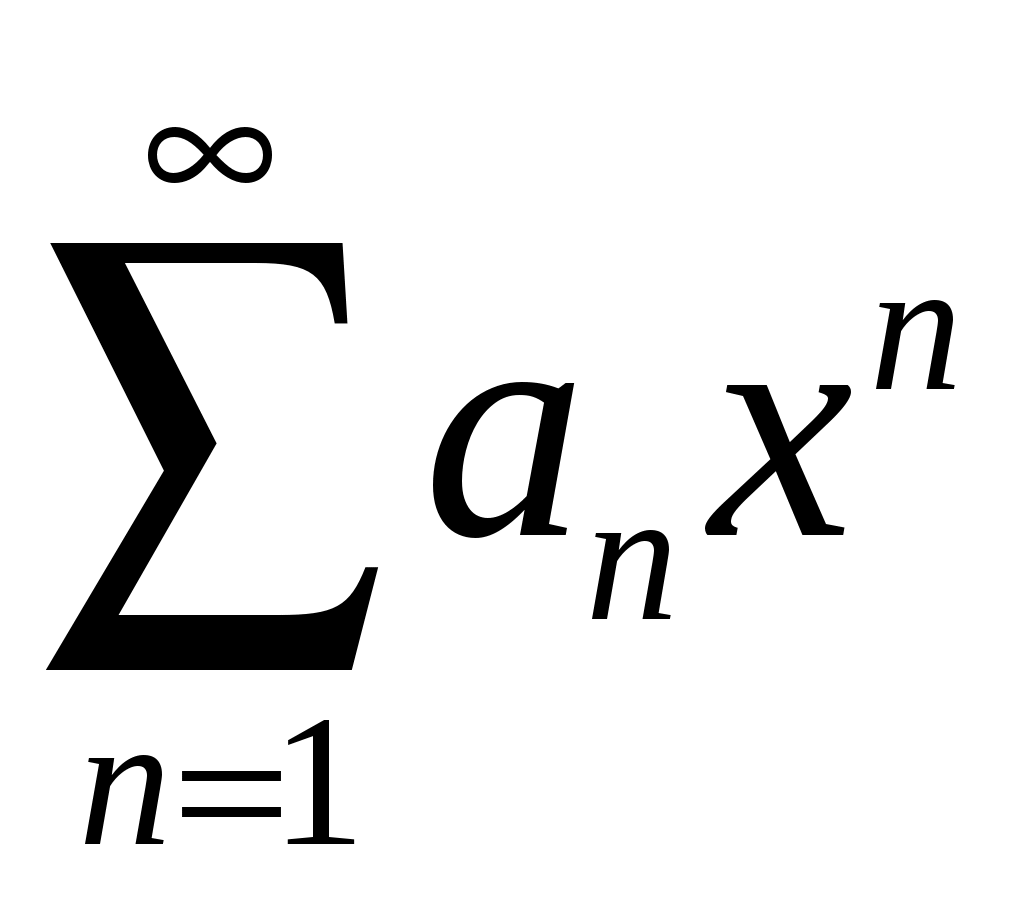 .
.Пример.
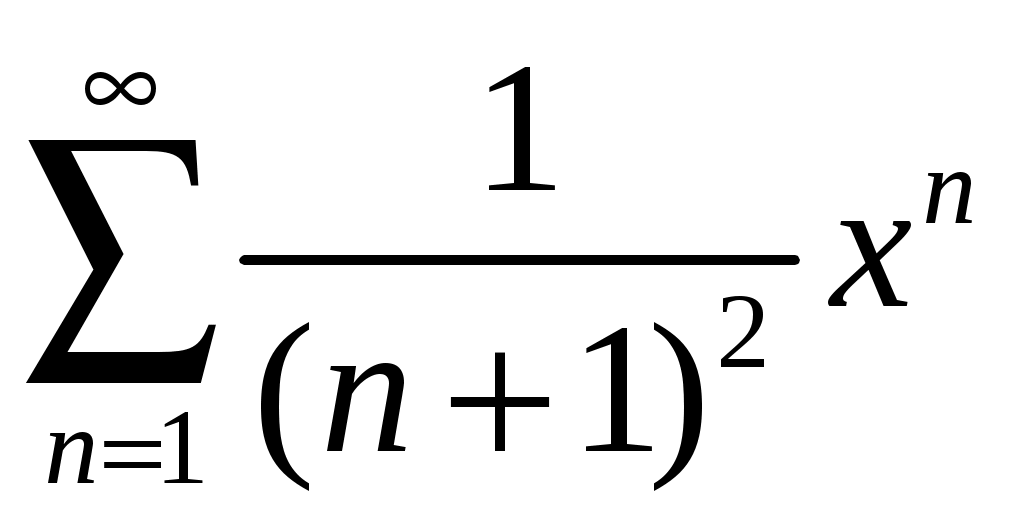 . Коэффициенты ряда:
. Коэффициенты ряда: 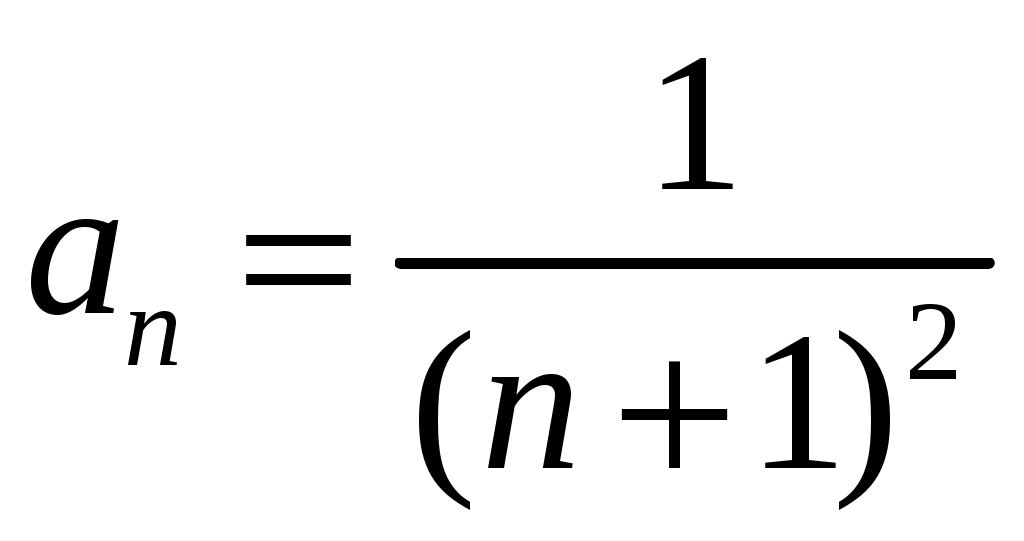 ,
, 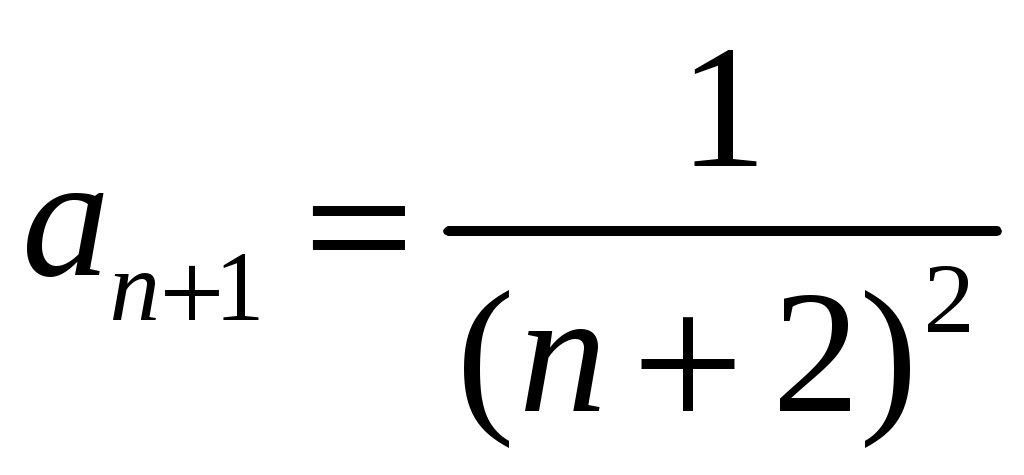 . Подставим их в формулу для радиуса сходимости степенного ряда:
. Подставим их в формулу для радиуса сходимости степенного ряда: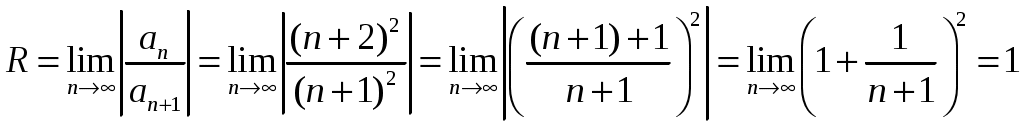 .
.Следовательно, ряд сходится для значений
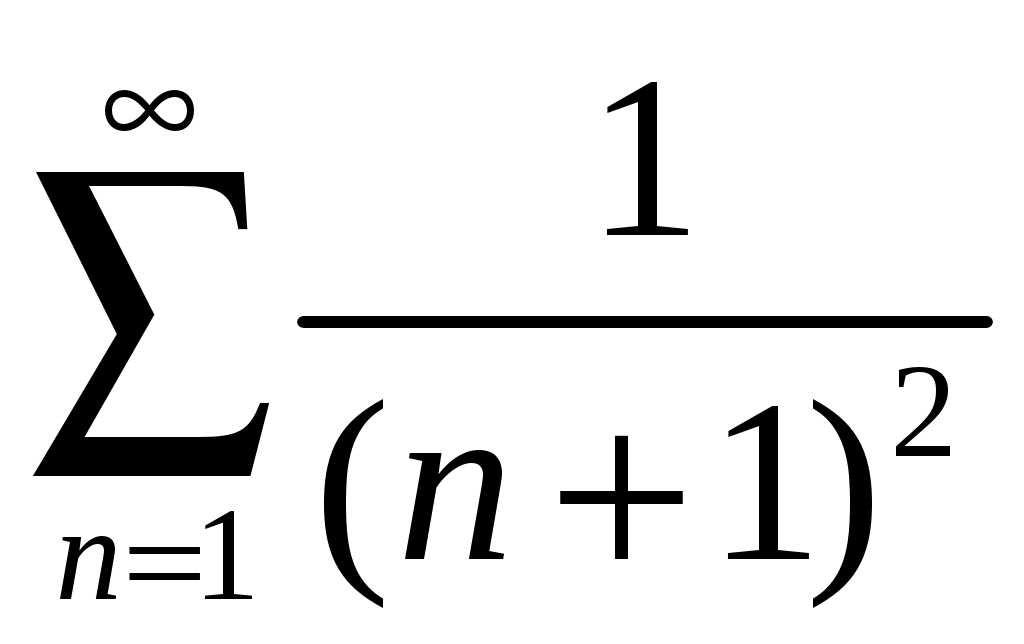 , который сходится, так как
, который сходится, так как Задание №6. Найти частные производные 1-го порядка.
Пример.
Задания №7 и № 8. Решить задачу по теории вероятности.
Пример 1. Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению и 20 задач по интегральному исчислению. Для сдачи зачета студент должен решить первый же доставшийся наугад билет из трех задач по одной задаче на каждую тему. Какова вероятность для студента сдать зачет,
если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение. Число билетов, которое может составить преподаватель, равно
Пример 2. Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению, 20 по интегральному исчислению. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение № 1. Студент знает 38 задач из пятидесяти, поэтому вероятность сдать зачет равна
Решение № 2. Вероятность получить задачу по пределам (событие