ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 52
Скачиваний: 2
СОДЕРЖАНИЕ
1. Определение закона движения механизма под действием заданных сил
1.3 Определение силы полезного сопротивления
1.4 Определение приведенного момента внешних сил
1.5 Определение работы суммарного приведенного момента
1.6 Определение приведенного момента инерции второй группы звеньев
1.7 Определение кинетической энергии 2 группы звеньев
1.8 Определение изменения кинетической энергии звеньев первой группы и момента инерции маховика
1.9 Определение угловой скорости начального звена
2.2 Определение сил, действующих на звенья механизма
2.3 Определение реакций в кинематических парах (структурная группа звеньев 2–3)
2.4 Силовой расчет ведущего звена
2.5 Определение уравновешивающего момента методом Жуковского
Для нашего механизма
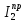 = m2 · (VS2 / 1)2 + m3 · (VВ / 1)2 + IS2 · (2 / 1)2.
= m2 · (VS2 / 1)2 + m3 · (VВ / 1)2 + IS2 · (2 / 1)2.Для 11 положения
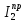 = 14 · (0,465 / 5,24) 2 + 18 · (0,53 / 5,24) 2 + 0,264 · (0,557 / 5,24) 2 ≈ 0,297 кгм2.
= 14 · (0,465 / 5,24) 2 + 18 · (0,53 / 5,24) 2 + 0,264 · (0,557 / 5,24) 2 ≈ 0,297 кгм2.Результаты расчёта
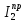 сведены в таблицу 3.
сведены в таблицу 3.Строим график
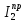 = ƒ(φ) в масштабе
= ƒ(φ) в масштабе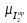 = 50 мм / 0,297 кгм2 168 мм/(кгм2).
= 50 мм / 0,297 кгм2 168 мм/(кгм2).Таблица 3 Приведенные моменты инерции звеньев второй группы
| φ, град | m2(Vs2/1)2, кгм2 | m3(VB/1)2, кгм2 | Is2(2/1)2, кг·м2 | 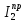 , кгм2 , кгм2 |
| 0 | 0,044 | 0 | 0,008 | 0,052 |
| 30 | 0,07 | 0,079 | 0,007 | 0,156 |
| 60 | 0,11 | 0,184 | 0,003 | 0,297 |
| 90 | 0,105 | 0,135 | 0 | 0,24 |
| 120 | 0,072 | 0,043 | 0,003 | 0,118 |
| 150 | 0,05 | 0,007 | 0,007 | 0,064 |
| 180 | 0,044 | 0 | 0,008 | 0,052 |
| 210 | 0,05 | 0,007 | 0,007 | 0,064 |
| 240 | 0,072 | 0,043 | 0,003 | 0,118 |
| 270 | 0,105 | 0,135 | 0 | 0,24 |
| 300 | 0,11 | 0,184 | 0,003 | 0,297 |
| 330 | 0,07 | 0,079 | 0,007 | 0,156 |
| 360 | 0,044 | 0 | 0,008 | 0,052 |
1.7 Определение кинетической энергии 2 группы звеньев
Кинетическая энергия Т2 определяется по формуле
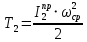 ,
,где ср – средняя угловая скорость начального звена, с-1.
ср = 1 = 5,24 с-1.
Так как величина
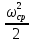 является постоянной, то характер изменения графика Т2(φ) будет таким же, что и графика
является постоянной, то характер изменения графика Т2(φ) будет таким же, что и графика  (φ); для расчета Т2 необходимо соответствующие ординаты графика
(φ); для расчета Т2 необходимо соответствующие ординаты графика  (φ) разделить на масштаб, который определяется по формуле:
(φ) разделить на масштаб, который определяется по формуле: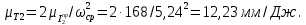
Результаты расчёта Т2 сведены в таблицу 4.
Таблица 4. Значения работ и кинетических энергий
| φ, град | Ас, Дж | АД, Дж | АΣ, Дж | Т2, Дж | ∆Т1, Дж |
| 0 | 0 | 0 | 0 | 0,71 | -0,71 |
| 30 | 7,68 | -25,78 | 33,76 | 2,14 | 35,9 |
| 60 | 13,01 | -51,56 | 64,57 | 4,08 | 68,65 |
| 90 | 15 | -77,32 | 92,31 | 3,29 | 95,6 |
| 120 | 13,01 | -103,13 | 116,14 | 1,62 | 117,76 |
| 150 | -7,68 | -128,91 | 121,23 | 0,82 | 122,05 |
| 180 | 0 | -154,69 | 154,69 | 0,71 | 155,4 |
| 210 | -7,43 | -186,08 | 178,65 | 0,82 | 179,47 |
| 240 | -12,8 | -214,78 | 201,98 | 1,62 | 203,6 |
| 270 | -40,42 | -245,45 | 205,03 | 3,29 | 208,32 |
| 300 | -197,19 | -287,43 | 90,24 | 4,08 | 94,32 |
| 330 | -275,57 | -300,27 | 24,7 | 2,14 | 26,84 |
| 360 | -309,39 | -309,39 | 0 | 0,71 | -0,71 |
1.8 Определение изменения кинетической энергии звеньев первой группы и момента инерции маховика
∆T1 = AΣ – T2.
Для 11-го положения
∆Т1 = 90,24 – 4,08 = 94,32 Дж.
Строим график ∆Т1=ƒ(φ) в масштабе
µT1 = 80 / 208,32 ≈ 0,384 мм/Дж.
Результаты расчёта ∆Т1 сведены в табл. 4.
Момент инерции маховика определяется по формуле
Iм = ∆T1наиб / (ср2 · ),
где ∆Т1наиб – наибольшее изменение кинетической энергии, Дж;
δ – коэффициент неравномерности движения начального звена.
∆T1наиб = ав / µT1 = 80,71 / 0,384 ≈ 210 Дж.
Iм = 210 Дж / ((5,24 с-1) 2 · 0,05) ≈ 153 кг·м2.
1.9 Определение угловой скорости начального звена
Определяя закон движения, воспользуемся тем, что при малых значениях коэффициента неравномерности δ график, изображающий изменение кинетической энергии ∆Т1, приближенно отражает изменение угловой скорости.