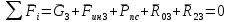ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 53
Скачиваний: 2
СОДЕРЖАНИЕ
1. Определение закона движения механизма под действием заданных сил
1.3 Определение силы полезного сопротивления
1.4 Определение приведенного момента внешних сил
1.5 Определение работы суммарного приведенного момента
1.6 Определение приведенного момента инерции второй группы звеньев
1.7 Определение кинетической энергии 2 группы звеньев
1.8 Определение изменения кинетической энергии звеньев первой группы и момента инерции маховика
1.9 Определение угловой скорости начального звена
2.2 Определение сил, действующих на звенья механизма
2.3 Определение реакций в кинематических парах (структурная группа звеньев 2–3)
2.4 Силовой расчет ведущего звена
2.5 Определение уравновешивающего момента методом Жуковского
Масштаб графика угловой скорости определяется по формуле:
µω = µT1 Iм ср;
µω = 0,384 153 5,24 ≈ 307 мм/c-1.
Максимальная и минимальная угловые скорости
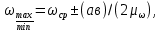
где ав – расстояние между высшей и низшей точками графика ∆Т1 = ƒ(φ), мм.
max = 5,24 + 80,71 / (2 307) ≈ 5,37 c-1;
min = 5,24 – 80,71 / (2 307) ≈ 5,11 c-1.
Проверка:
ср = (max +min) / 2 = (5,37 + 5,11) / 2 = 5,24 c-1;
= (max – min) / ср = (5,37 – 5,11) / 5,24 = 0,05.
Расстояние от линии 1=ср до оси 1=0
Y = ср µω = 5,24 × 307 ≈ 1608 мм.
2. Силовой расчет механизма
Построим кинематическую схему механизма для одного заданного положения в масштабе:
μl = 500 мм/м.
Построим план скоростей для заданного положения механизма в масштабе μV = |pa|/ VA (см. гл. 1):
μV = 50 мм / 0,7336 м·с-1 =68,16 мм/м·с-1.
2.1 Определение ускорений
Ускорение точки А:
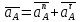 ;
;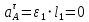 , т. к. 1 = const;
, т. к. 1 = const;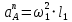 = (5,24 c-1)2 0,14 м = 3,84 мс-2.
= (5,24 c-1)2 0,14 м = 3,84 мс-2.Ускорение точки В:
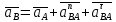 ;
;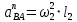 = (0,53)2 0,476 м = 0,133 мс–2.
= (0,53)2 0,476 м = 0,133 мс–2.Построим план ускорений в масштабе
μa = |a| / aA,
где a – отрезок на плане ускорений, соответствующий ускорению точки А(аA): μа = 50 мм / 3,84 мс-2 = 13,02 мм/мс-2.
Неизвестные величины aB, aBA,
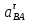 ,
, 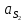 найдем из плана ускорений:
найдем из плана ускорений:aB = 10,52 мм / 13,02 мм/мс-2 = 0,807 мс-2;
aBA = 45,43
мм / 13,02 мм/мс-2 = 3,48 мс-2;
 = 45,65 мм / 13,02 мм/мс-2 = 3,5 мс-2;
= 45,65 мм / 13,02 мм/мс-2 = 3,5 мс-2; = 32,31 мм / 13,02 мм/мс-2 = 2,48 мс-2.
= 32,31 мм / 13,02 мм/мс-2 = 2,48 мс-2.Угловое ускорения 2-го звена:
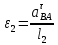 = 3,5 мс-2 / 0,476 м = 7,35 c-2.
= 3,5 мс-2 / 0,476 м = 7,35 c-2.2.2 Определение сил, действующих на звенья механизма
Силы тяжести (см. гл. 1):
G2 = 137 H;
G3 = 176 H.
Силы инерции
Fинi = – mi ai,
где аi – ускорение центра масс i-го звена, мс-2.
Fин2 = – m2 aS2 = – 14 кг 2,48 мс-2 = – 35 Н;
Fин3 = – m3 aB = – 18 кг 0,807 мс-2 = – 14,5 Н.
Знак «–» свидетельствует о том, что сила инерции направлена в сторону, противоположную ускорению центра масс.
Момент инерции, действующий на 2-е звено:
Мин2 = – IS2 ε2 = – 0,25 кгм2 7,35 с-2 = – 1,83 Н·м.
Знак «–» означает то, что момент инерции направлен в сторону
, противоположную угловому ускорению.
Сила полезного сопротивления (см. гл. 1):
Рпс(11) = 2846 Н.
2.3 Определение реакций в кинематических парах (структурная группа звеньев 2–3)
Составляем уравнение:
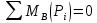 или
или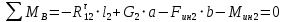 ,
,где а, b – плечи действия сил Fин2 и G2, м.
b = 133 мм / 500 мм/м = 0,266 м;
a = 150 мм / 500 мм/м = 0,3 м.
Из этого уравнения находим
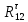 :
: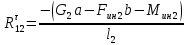 = – (137 0,3 – 35 0,266 – 1,83) / 0,476 = 70 H.
= – (137 0,3 – 35 0,266 – 1,83) / 0,476 = 70 H.Составляем следующее уравнение равновесия:
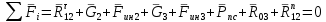 ,
,где R03 – реакция в поступательной кинематической паре;
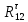 ,
, 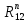 – касательная и нормальная составляющие реакции в шарнире А.
– касательная и нормальная составляющие реакции в шарнире А.Неизвестные реакции R03 и
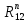 , а также R12 найдем из плана сил, который построим в масштабе μР.
, а также R12 найдем из плана сил, который построим в масштабе μР.μР = 100 мм / Pпс = 100 мм / 2846 H = 0,036 мм/H;
R03 = 59,7 мм / 0,036 мм/H = 1658 Н;
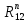 = 109 мм / 0,036 = 3027 H;
= 109 мм / 0,036 = 3027 H;R12 = 110 мм / 0,036 = 3055 H.
Определяем реакцию во вращательной кинематической паре В (R23).
Отделяем звено 3 и составляем для него векторное уравнение равновесия: