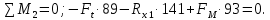Файл: Введение Кинематический расчет и выбор электродвигателя.docx
Добавлен: 09.11.2023
Просмотров: 131
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
элементов соединений «вал-ступица» [1, п. 10.1, 10.2, стр.125]:
-параллельность шпоночного паза к оси вала (втулки)-0,5ITn его ширины;
- симметричность шпоночного паза 2 ITn его ширины.
РАБОЧИЙ ЧЕРТЕЖ ЦИЛИНДРИЧЕСКОГО КОЛЕСА – [1, стр.140]:
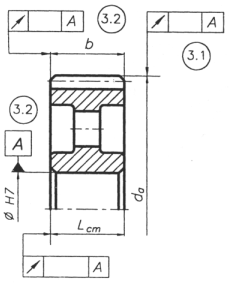
-допуск радиального биения , мкм поверхности заготовки под диаметр вершин зубьев относительно поверхности А [1, табл. 11.2.5, стр.140]:
, мкм поверхности заготовки под диаметр вершин зубьев относительно поверхности А [1, табл. 11.2.5, стр.140]:
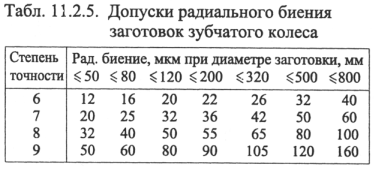
-допуск осевого биения , мкм, ступицы колеса и базовых поверхностей венца относительно поверхности А [1, табл. 1.2.6, стр.140]:
, мкм, ступицы колеса и базовых поверхностей венца относительно поверхности А [1, табл. 1.2.6, стр.140]:
Назначаем посадки основных деталей редуктора:
– зубчатых колес на валы Н7/p6;
– муфт на валы редуктора H7/k6;
– фланцев в корпус H7/d9;
– шпонки в вал P9/h9;
– шпонки в ступицу P9/h9.
Шейки валов под подшипники выполняем с отклонением вала k6, отклонения отверстий в корпусе под наружные кольца подшипников Н7.
Отклонения вала в месте соприкосновения с манжетой по h8.
11. Расчёт валов на выносливость
Схема быстроходного вала представлена на рисунке 8.1
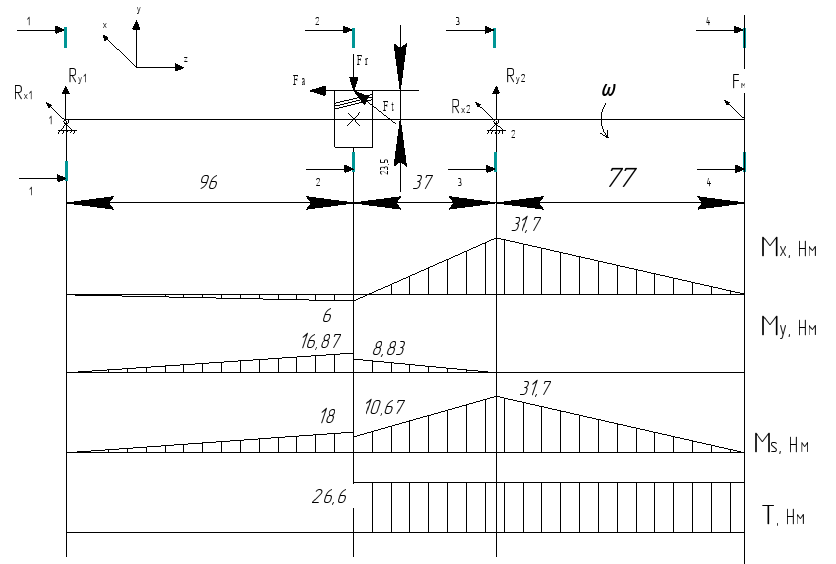
Рисунок 11.1
Определяем реакции опор вала из уравнения равновесия.
Плоскость ZX:
Сумма моментов относительно точки 1:
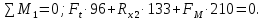
Отсюда находим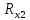 :
:
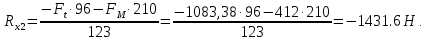
Сумма моментов относительно точки 2:
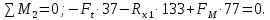
Отсюда находим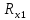 :
:
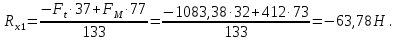
Проверка:
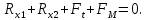
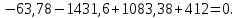
Плоскость ZY:
Сумма моментов относительно точки 1:
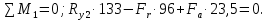
Отсюда находим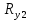 :
:
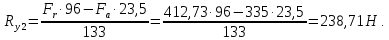
Сумма моментов относительно точки 2:
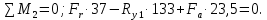
Отсюда находим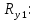
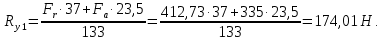
Проверка:
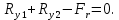
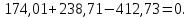
Определяем суммарные реакции в опорах:
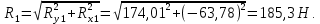
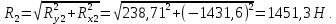
Построение эпюр изгибающих и крутящих моментов
Изгибающие моменты в плоскости ZX:
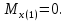
С левой стороны от сечения 2:
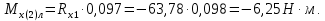
С правой стороны от сечения 2:
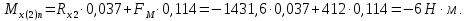
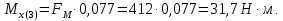
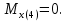
Изгибающие моменты в плоскости ZY:
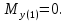
С левой стороны от сечения 2:
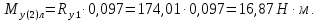
С правой стороны от сечения 2:
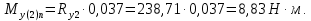
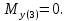
Суммарный изгибающий момент:
С левой стороны от сечения 2:
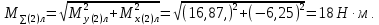
С правой стороны от сечения 2:
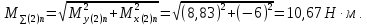
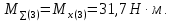
 Крутящий момент на быстроходном валу численно равен вращающему:
Крутящий момент на быстроходном валу численно равен вращающему:
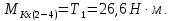
Схема промежуточного вала представлена на рисунке 11.2
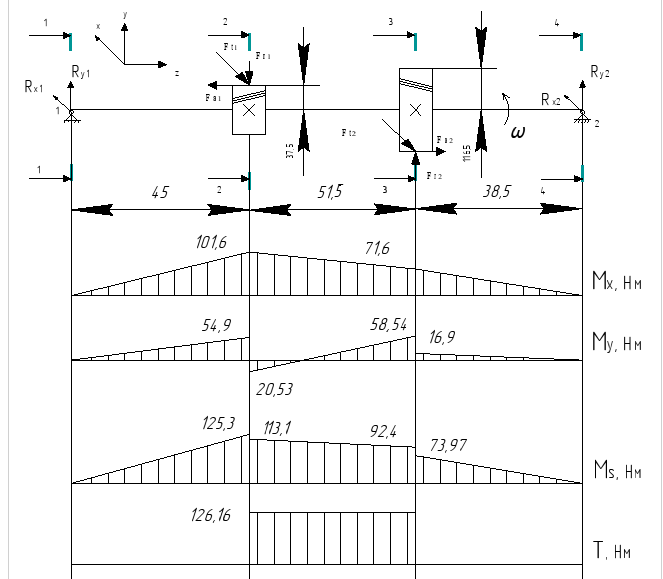
Рисунок 11.2
Определяем реакции опор вала из уравнения равновесия.
Плоскость ZX:
Сумма моментов относительно точки 1:
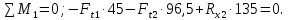
Отсюда находим :
:
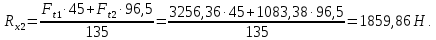
Сумма моментов относительно точки 2:
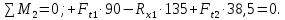
Отсюда находим :
:
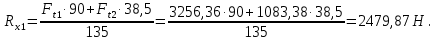
Проверка:
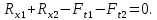
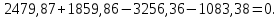
Плоскость ZY:
Сумма моментов относительно точки 1:
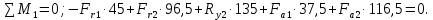
Отсюда находим :
:
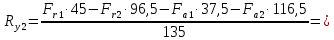
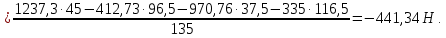
Сумма моментов относительно точки 2:

Отсюда находим
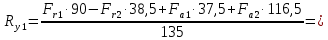
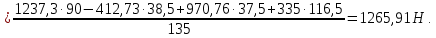
Проверка:
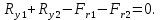
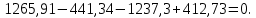
Определяем суммарные реакции в опорах:
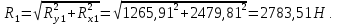
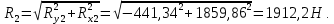
Построение эпюр изгибающих и крутящего моментов
Изгибающие моменты в плоскости ZX:

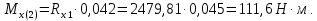
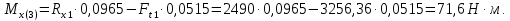
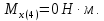
Изгибающие моменты в плоскости ZY:

С левой стороны от сечения 2:
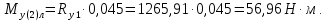
С правой стороны от сечения 2:
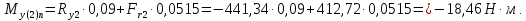
С левой стороны от сечения 3:
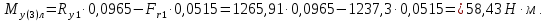
С правой стороны от сечения 3:
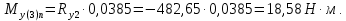
Суммарный изгибающий момент:
С левой стороны от сечения 2:
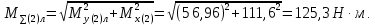
С правой стороны от сечения 2:
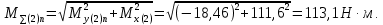
С левой стороны от сечения 3:

С правой стороны от сечения 3:
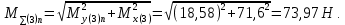
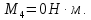
 Крутящий момент на промежуточном валу численно равен вращающему:
Крутящий момент на промежуточном валу численно равен вращающему:
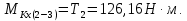
Построение эпюр изгибающих и крутящего моментов
Изгибающие моменты в плоскости ZX:




Изгибающие моменты в плоскости ZY:

С левой стороны от сечения 2:

С правой стороны от сечения 2:

С левой стороны от сечения 3:

С правой стороны от сечения 3:

Суммарный изгибающий момент:
С левой стороны от сечения 2:

С правой стороны от сечения 2:

С левой стороны от сечения 3:

С правой стороны от сечения 3:


 Крутящий момент на промежуточном валу численно равен вращающему:
Крутящий момент на промежуточном валу численно равен вращающему:
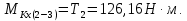
Схема вала представлена на рисунке 11.3.
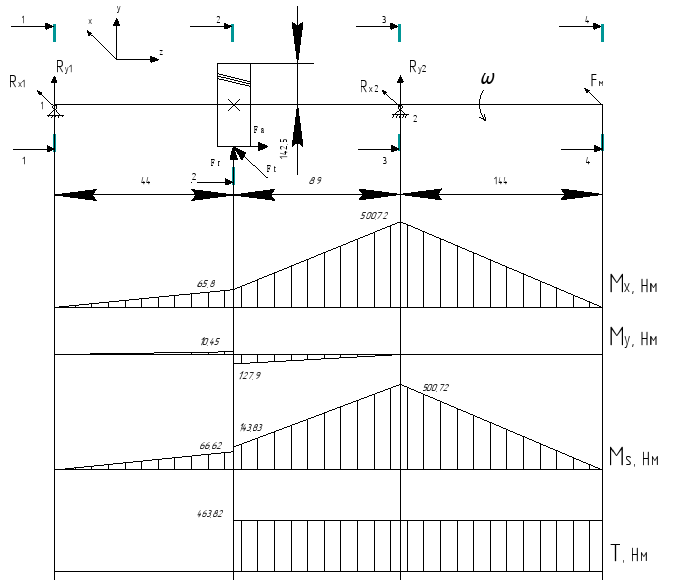
Рисунок 11.3
Определяем реакции опор вала из уравнения равновесия.
Плоскость ZX:
Сумма моментов относительно точки 1:
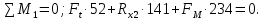
Отсюда находим :
:
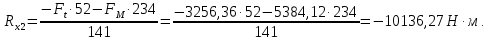
Сумма моментов относительно точки 2:
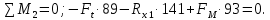
-параллельность шпоночного паза к оси вала (втулки)-0,5ITn его ширины;
- симметричность шпоночного паза 2 ITn его ширины.
РАБОЧИЙ ЧЕРТЕЖ ЦИЛИНДРИЧЕСКОГО КОЛЕСА – [1, стр.140]:

-допуск радиального биения

-допуск осевого биения

Назначаем посадки основных деталей редуктора:
– зубчатых колес на валы Н7/p6;
– муфт на валы редуктора H7/k6;
– фланцев в корпус H7/d9;
– шпонки в вал P9/h9;
– шпонки в ступицу P9/h9.
Шейки валов под подшипники выполняем с отклонением вала k6, отклонения отверстий в корпусе под наружные кольца подшипников Н7.
Отклонения вала в месте соприкосновения с манжетой по h8.
11. Расчёт валов на выносливость
11.1 Быстроходный вал
Определение реакций опор и построение эпюр
Схема быстроходного вала представлена на рисунке 8.1

Рисунок 11.1
Определяем реакции опор вала из уравнения равновесия.
Плоскость ZX:
Сумма моментов относительно точки 1:
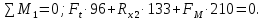
Отсюда находим
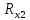 :
: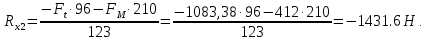
Сумма моментов относительно точки 2:
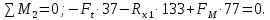
Отсюда находим
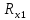 :
: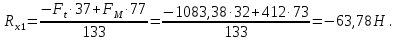
Проверка:
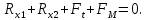
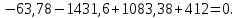
Плоскость ZY:
Сумма моментов относительно точки 1:
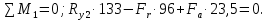
Отсюда находим
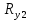 :
: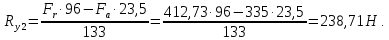
Сумма моментов относительно точки 2:
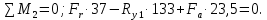
Отсюда находим
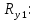
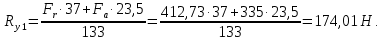
Проверка:
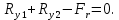
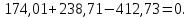
Определяем суммарные реакции в опорах:
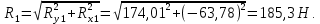
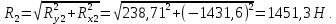
Построение эпюр изгибающих и крутящих моментов
Изгибающие моменты в плоскости ZX:
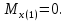
С левой стороны от сечения 2:
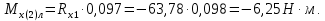
С правой стороны от сечения 2:
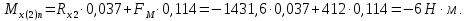
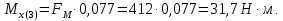
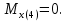
Изгибающие моменты в плоскости ZY:
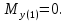
С левой стороны от сечения 2:
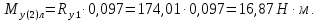
С правой стороны от сечения 2:
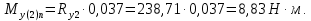
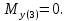
Суммарный изгибающий момент:
С левой стороны от сечения 2:
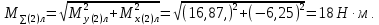
С правой стороны от сечения 2:
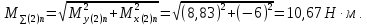
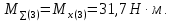
 Крутящий момент на быстроходном валу численно равен вращающему:
Крутящий момент на быстроходном валу численно равен вращающему: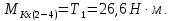
11.2 Промежуточный вал
Определение реакций опор и построение эпюр
Схема промежуточного вала представлена на рисунке 11.2

Рисунок 11.2
Определяем реакции опор вала из уравнения равновесия.
Плоскость ZX:
Сумма моментов относительно точки 1:
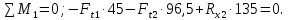
Отсюда находим
 :
: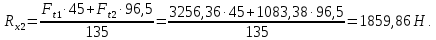
Сумма моментов относительно точки 2:
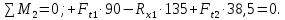
Отсюда находим
 :
: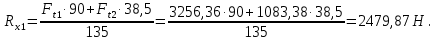
Проверка:
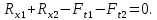
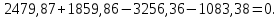
Плоскость ZY:
Сумма моментов относительно точки 1:
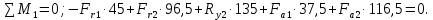
Отсюда находим
 :
: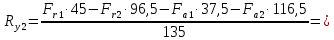
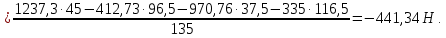
Сумма моментов относительно точки 2:

Отсюда находим

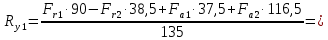
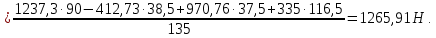
Проверка:
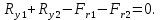
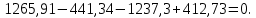
Определяем суммарные реакции в опорах:
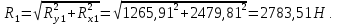
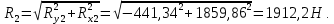
Построение эпюр изгибающих и крутящего моментов
Изгибающие моменты в плоскости ZX:

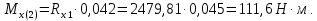
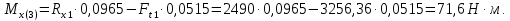
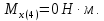
Изгибающие моменты в плоскости ZY:

С левой стороны от сечения 2:
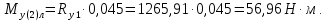
С правой стороны от сечения 2:
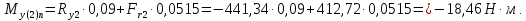
С левой стороны от сечения 3:
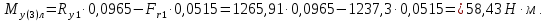
С правой стороны от сечения 3:
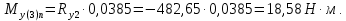
Суммарный изгибающий момент:
С левой стороны от сечения 2:
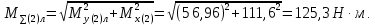
С правой стороны от сечения 2:
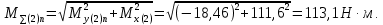
С левой стороны от сечения 3:

С правой стороны от сечения 3:
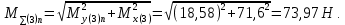
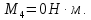
 Крутящий момент на промежуточном валу численно равен вращающему:
Крутящий момент на промежуточном валу численно равен вращающему:
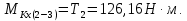
Построение эпюр изгибающих и крутящего моментов
Изгибающие моменты в плоскости ZX:




Изгибающие моменты в плоскости ZY:

С левой стороны от сечения 2:

С правой стороны от сечения 2:

С левой стороны от сечения 3:

С правой стороны от сечения 3:

Суммарный изгибающий момент:
С левой стороны от сечения 2:

С правой стороны от сечения 2:

С левой стороны от сечения 3:

С правой стороны от сечения 3:


 Крутящий момент на промежуточном валу численно равен вращающему:
Крутящий момент на промежуточном валу численно равен вращающему: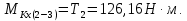
11.3 Тихоходный вал
Определение реакций опор и построение эпюр
Схема вала представлена на рисунке 11.3.

Рисунок 11.3
Определяем реакции опор вала из уравнения равновесия.
Плоскость ZX:
Сумма моментов относительно точки 1:
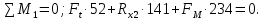
Отсюда находим
 :
: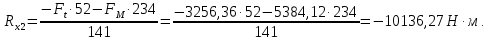
Сумма моментов относительно точки 2: