Файл: Учебное пособие для практических занятий по дисциплине Финансовый менеджмент.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 318
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3.3. Определение размера и современной стоимости потока лизинговых
1.2. Наращение и дисконтирование с использованием ставки сложных процентов
1.3. Финансовые ренты (постнумерандо и пренумерандо)
1.4. Оценка эффективности финансовых операций
2.2. Общий случай изменения условий коммерческих сделок
3.3. Определение размера и современной стоимости потока лизинговых платежей
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Российский университет транспорта (МИИТ)»
Институт экономики и финансов
Кафедра «Финансы и кредит»
А.А. Орлов
Методология и практика финансовых вычислений
Учебное пособие
для студентов экономических, технических профилей
и специальностей
Москва – 2019
УДК 336.64.072
0-66
Орлов А.А. Методология и практика финансовых вычислений: Учебное пособие для практических занятий по дисциплине «Финансовый менеджмент». - М.: РУТ (МИИТ), 2019. - 60 с.
В учебном пособии в систематизированном виде в соответствии с программой дисциплины «Финансовый менеджмент» изложены методики и примеры решения задач, которые возникают не только перед экономистами, финансистами, банкирами и прочими специалистами в плане их профессиональной деятельности, связанной с финансовыми вычислениями и расчетами, но и перед обычными людьми в их повседневной жизни.
Каждый методический подход сопровождается решением конкретных примеров, усвоение которых позволяет реализовать теоретические знания в области практических финансово-экономических расчетов.
Рекомендуется студентам экономических, технических профилей и программ обучения, широкому кругу обычных читателей.
Рецензенты:
- к.э.н., действительный член Института профессиональных бухгалтеров России (ИПБ России), ведущий специалист Ассоциации МСОПАУ
Демидов А.В.;
- старший преподаватель кафедры МФиУУ РУТ (МИИТ) Нуриманов Р.Н.
© РУТ (МИИТ), 2019
ОГЛАВЛЕНИЕ стр.
1. ОСНОВЫ ТЕОРИИ ФИНАНСОВЫХ РАСЧЕТОВ .…….………………..…4
1.1. Простые проценты, наращение и дисконтирование ……………………..…4
1.2. Наращение и дисконтирование с использованием ставки сложных
процентов …………………………………………………………………….……6
1.3. Финансовые ренты (постнумерандо и пренумерандо)…..……….................7
1.4. Оценка эффективности финансовых операций ……..………………............8
1.5. Расчеты в условиях инфляции ………………………….……….................... 9
1.6. Кредитные операции …………………………………….…………….........10
2. ИЗМЕНЕНИЕ УСЛОВИЙ ПЛАТЕЖЕЙ ПО ФИНАНСОВЫМ
ОБЯЗАТЕЛЬСТВАМ …………………………………………............................ 18
2.1. Частный случай изменения условий платежей ……………….…………...18
2.2. Общий случай изменения условий коммерческих сделок ……………......20
2.3. Конверсия займов …………………………………………………..……... 21
2.4. Консолидация займов ………………………………………………….….…21
2.5. Реструктурирование займов ……………………………………….………. 22
2.6. Конверсия, консолидация финансовых рент …………………………….. 22
3. МЕТОДЫ АНАЛИЗА И ОЦЕНКИ УСЛОВИЙ КОММЕРЧЕСКИХ КОНТРАКТОВ…………………………………………………………………….25
3.1. Теория решения задач, конкурентными условиями которых являются схемы поставок и условия погашения задолженности ………………………...27
3.2. Аренда, лизинг или покупка. Определение наиболее выгодного варианта
приобретения имущества ……………………………………………………….. 38
3.3. Определение размера и современной стоимости потока лизинговых
платежей …………………………………………………………………….....… 47
3.4. Ипотека. Определение размера платежа и современной стоимости
потоков платежей ………………….………………………………………......…51
3.5. Анализ и планирование капитальных вложений …………………………..53
3.5.1 Производственные инвестиции……………….. ………………………......54
3.5.2. Инвестиции в ценные бумаги………………………………….…..….…...56
Список использованной литературы…………............................. ..59
ПРИЛОЖЕНИЕ Таблица «Порядковые номера дней в году»…………….…..60
1. ОСНОВЫ ТЕОРИИ финансовых РАСЧЕТОВ
1.1. Простые и сложные проценты, наращение и дисконтирование
Наращение по ставке простых процентов
Р – первоначальная сумма;
i – ставка % из расчета годовых;
n – период наращения в годах.
Сумма начисленных процентов (I):
Наращенная сумма (
):
Если период наращения выражается в днях, то в формулы (1.2. и 1.3.) вместо
где
Определение продолжительности периода наращения
Задача 1.1. Определить период наращения (срок вклада) в днях для начисления простых процентов при различной практике их начисления, если вклад до востребования был размещен с 25 июня 2019 г. по 5 сентября 2019 г.
Решение
Германская (немецкая) практика (период наращения месяца открытия вклада всегда считаем вычитанием даты открытия вклада (25) из его фактической (28, 29, 30, или 31 день) длительности, каждый следующий полный месяц периода наращения берется равным 30 дням, а период наращения месяца закрытия определяется датой закрытия ):
июнь + июль + август + сентябрь
Французская и английская практика (отличается только тем, что каждый полный месяц берется фактической календарной длительности):
июнь + июль + август + сентябрь
Период наращения в годах можно определить по формулам:
Германская практика
Французская
Для определения периода наращения для французской и английской практики (
Порядковый номер 25 июня –176. Порядковый номер 5 сентября – 248.
Период наращения точно определится как разница двух чисел:
248 - 176 = 72 дня
Задача 1.2. (для самостоятельного решения). Вклад был открыт 12 марта 2019 г. и востребован 25 декабря 2019 г. Определить период наращения для французской практики начисления процентов.
Ответ: 288 дней
Определение наращенной суммы или суммы процентов в случае, если ставка процента или сумма на счете изменяются в течение срока хранения вклада
При изменении суммы вклада в течение срока хранения (или периода наращения) общая сумма процентов за весь срок может быть определена как сумма процентов, начисленных для каждого периода начисления, на котором сумма на счёте или ставка были постоянными:
Наращенная сумма определяется по формуле:
Операции дисконтирования по простой процентной ставке
Обратная задача - по известной наращенной сумме определяется сумма первоначального взноса, обеспечивающая накопление заданной наращенной суммы.
Известны:
-
математическое дисконтирование:
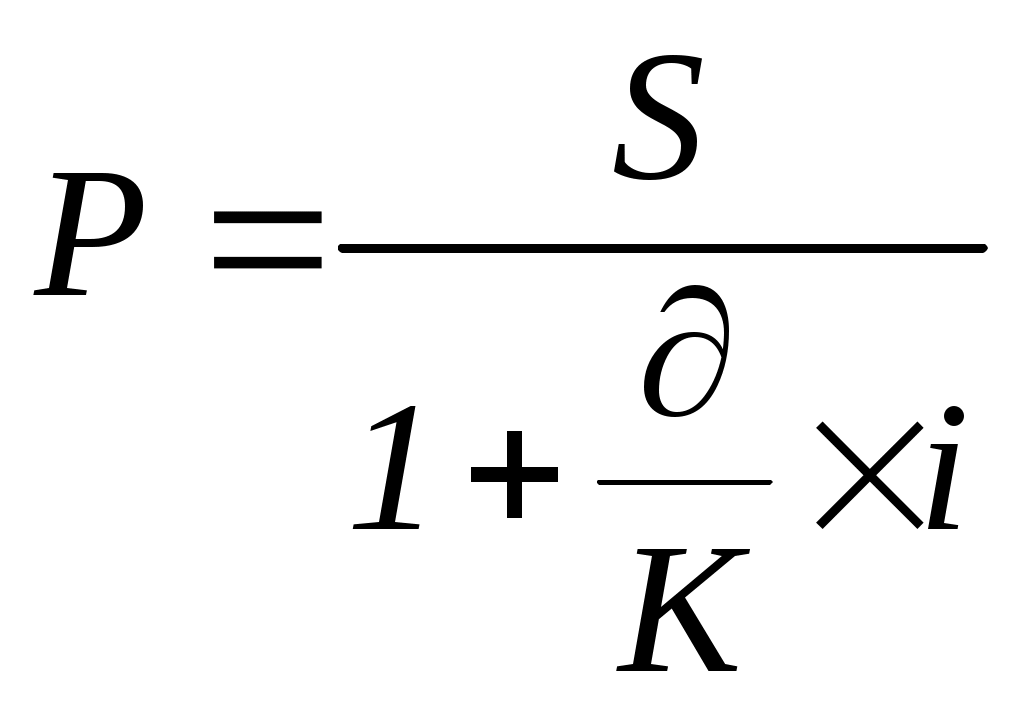 (1.8) или
(1.8) или где V
i - коэффициент дисконтирования;
2) банковский учёт(применяется, как правило, в операциях с векселями):
где
Как правило, в операции дисконтирования используется французская практика (
Из формул:
можно при прочих заданных условиях определить, соответственно, период наращения в годах и днях, ставку простых процентов. Например, период наращения в годах при прочих заданных условиях определится по формуле: