Файл: Учебное пособие для практических занятий по дисциплине Финансовый менеджмент.doc

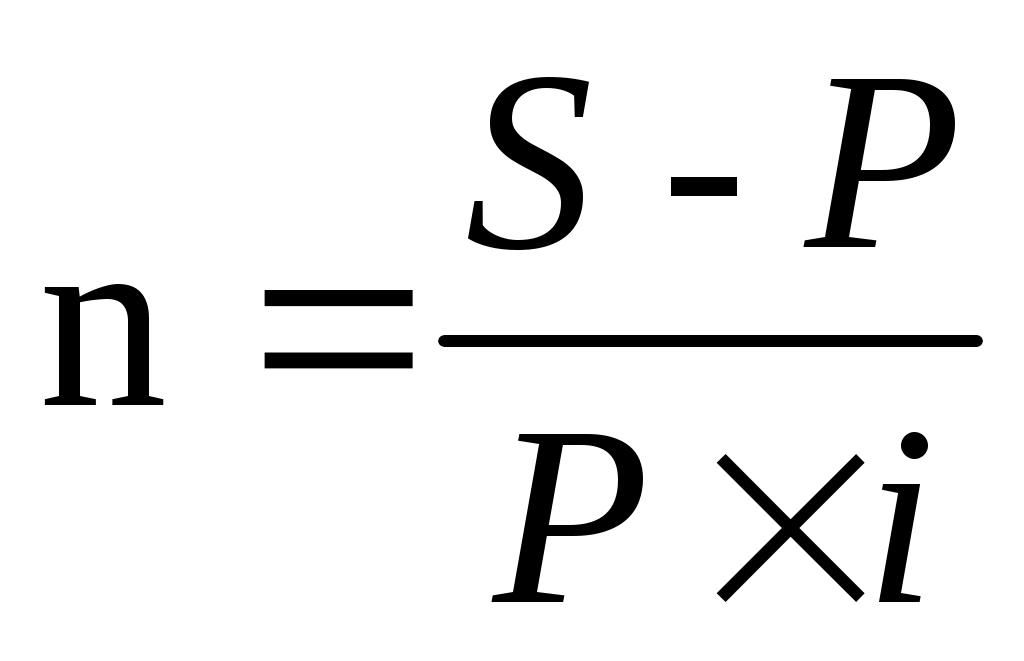(1.12)

1.2. Наращение и дисконтирование с использованием ставки сложных процентов

Наращенная сумма при использовании ставки сложных процентов определяется по формулам:

(1.13) или (1.14)

Если сложные проценты будут начисляться несколько раз в году (m – раз, если ежемесячно, то m=12, ежеквартально – m= 4, ежедневно – m=365 раз)

(1.15)

Из формул для определения наращенной суммы можно вывести формулы:

- для определения значения первоначальной суммы, обеспечивающей накопление заданной суммы при прочих известных условиях, т.е. выполнить операцию дисконтирования будущей суммы:

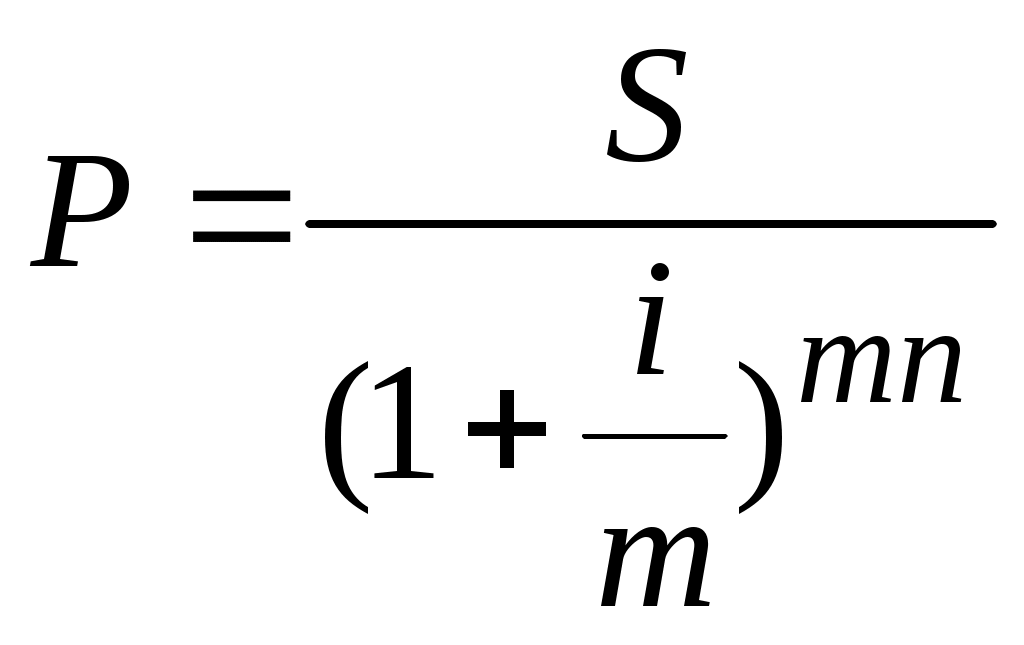(1.16) (1.17) (1.18)

- ставки сложных процентов: (1.19)

- периода наращения: 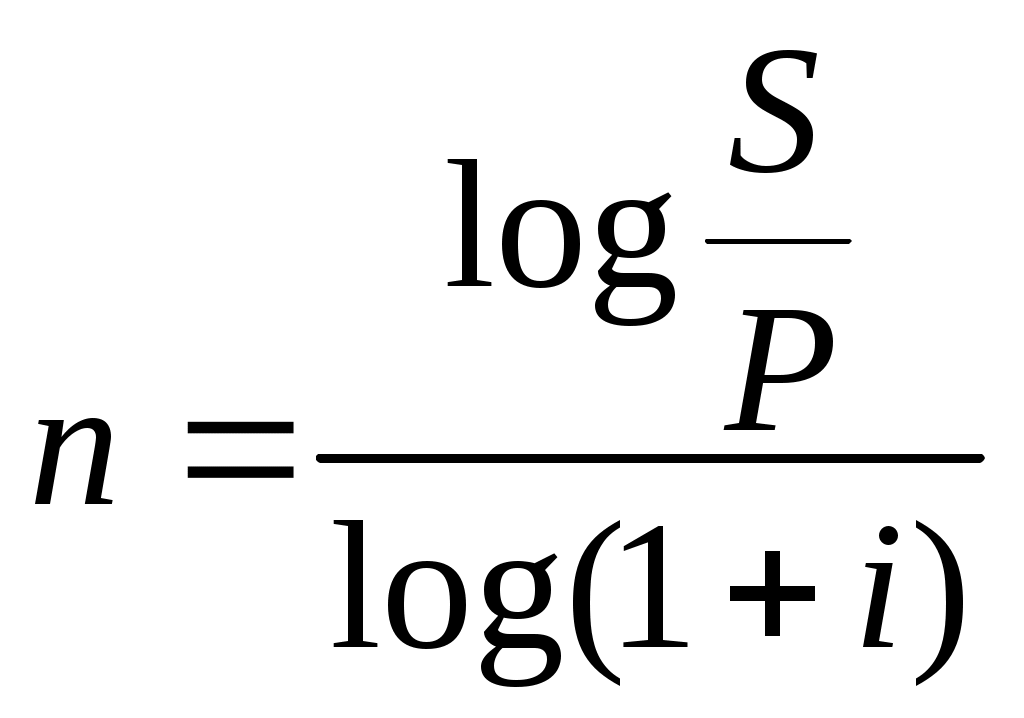(1.20)
Задача 1.3. Президент России В.В. Путин в 2005 г. поставил задачу удвоения ВВП к 2010 г. Определить годовые темпы прироста ВВП обеспечивающие выполнение поставленной задачи ( за 5 лет).
Решение

Темпы прироста ВВП – это ставка сложных процентов, которая, как и в предыдущей задаче, определится по формуле:

Для решения задачи абсолютные величины не нужны, т.к. нам известно отношение S/ P = 2 и n = 5 лет.

Ответ: 0,1487 в долях единиц или 14,87 %

1.3. Финансовые ренты (постнумерандо и пренумерандо)

Последовательность денежных поступлений, осуществляемых равными суммами через равные периоды (промежутки) времени, называют постоянной финансовой рентой.

---

Различают:

- ренту постнумерандо (платежи в конце периода - года, квартала, месяца)

- ренту пренумерандо (платежи в начале периода - года, квартала, месяца)

Пусть в течение -лет на счет вносится одна и та же сумма - член ренты. На взносы также один раз в год начисляются сложные проценты по ставке -% годовых. Наращенная сумма рентных платежей в этом случае определится по формулам (соответственно, рента пренумерандо и рента постнумерандо):

(1.21) (1.22)

Если взносы в размере будут вноситься - раз в году (в конце или начале расчётных периодов) и на суммы на счёте - раз в году будут начисляться сложные проценты по годовой ставке , то наращенная сумма взносов за - лет в этом случае определится по формулам:

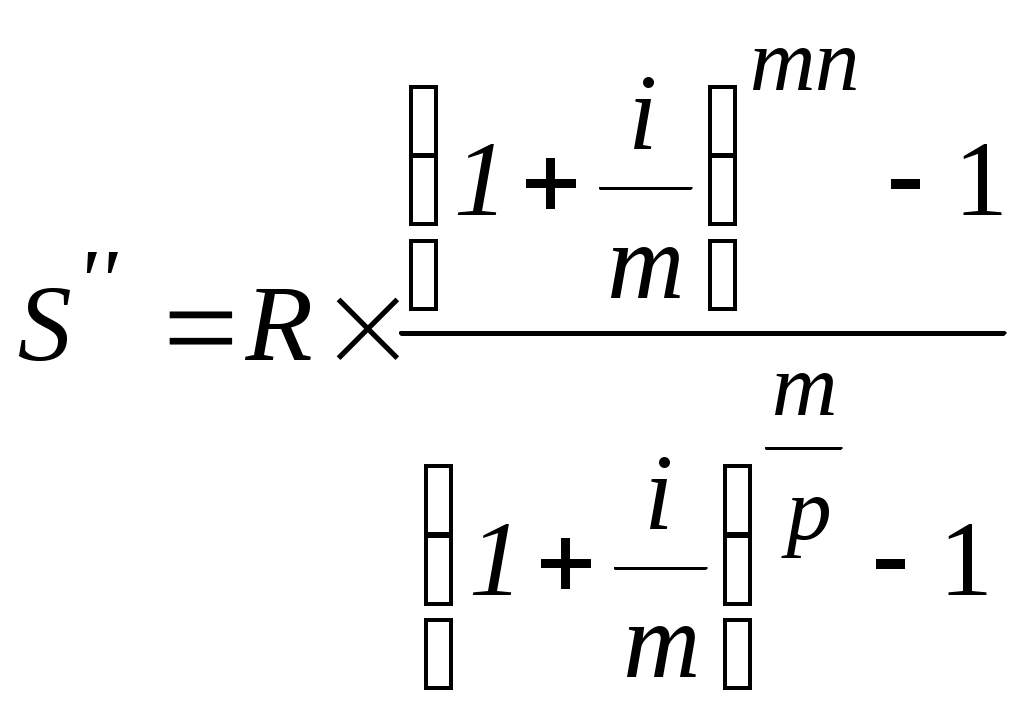(1.23) 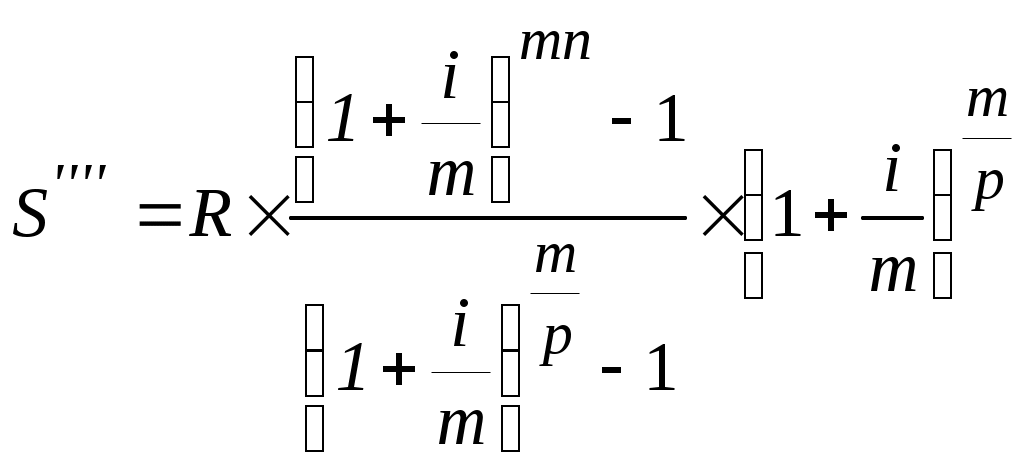(1.24)

Из приведенных формул путем несложных математических преобразований можно вывести формулы для определения размера взносов, обеспечивающих накопление заданной суммы. Например, размер члена ренты постнумерандо можно определить по формуле:

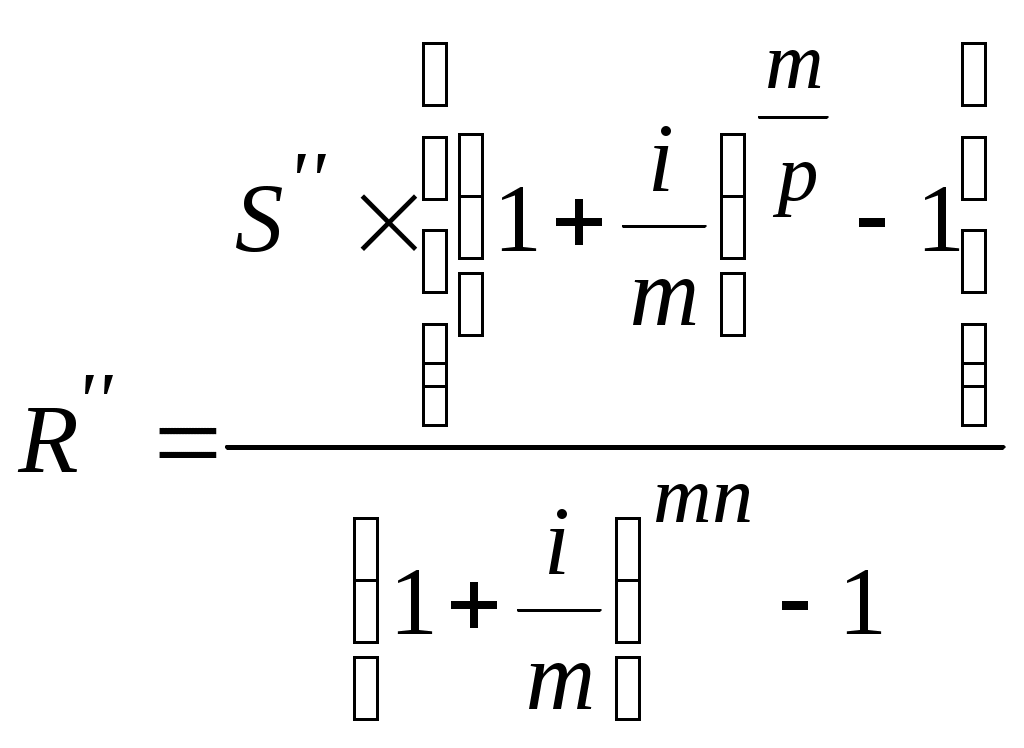(1.25)
Задача 1.4. На депозитный счет ежемесячно в конце месяца в течение 5 лет будут вносить по 500 руб. На сумму счета также в конце каждого месяца будут начисляться сложные проценты по ставке 22% годовых. Определить сумму, которую получит вкладчик при закрытии счета.

---

Решение

Наращенная сумма ренты постнумерандо в общем виде определяется по формуле:

(1.22) 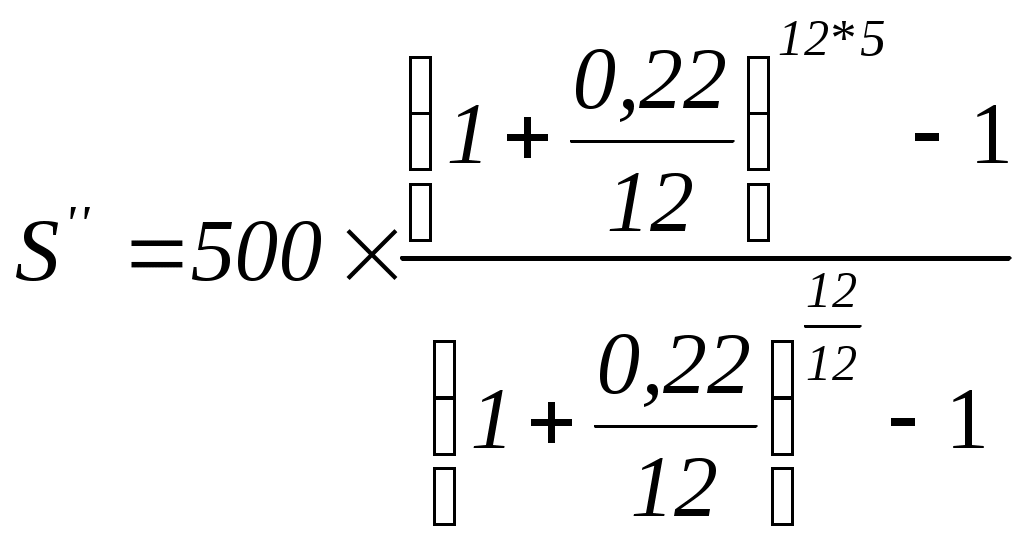= 53847 (тыс. руб.)

Ответ: 53847 тыс. руб.
Задача 1.5. (для самостоятельного решения). Взносы в накопительный пенсионный фонд будут производиться в начале каждого месяца и на них ежеквартально будут начисляться сложные проценты по ставке 36% годовых. Определить размер взноса, если за 40 лет в фонде должна быть накоплена сумма 1 млн. руб.

Ответ: 3 копейки

---

1.4. Оценка эффективности финансовых операций

Показателем, выступающем в качестве меры эффективности вложений средств при различных условиях, является эквивалентная (эффективная) годовая ставка простых или сложных процентов ( ).

При начислении процентов m - раз в году эффективная ставка сложных процентов может иметь следующий вид:

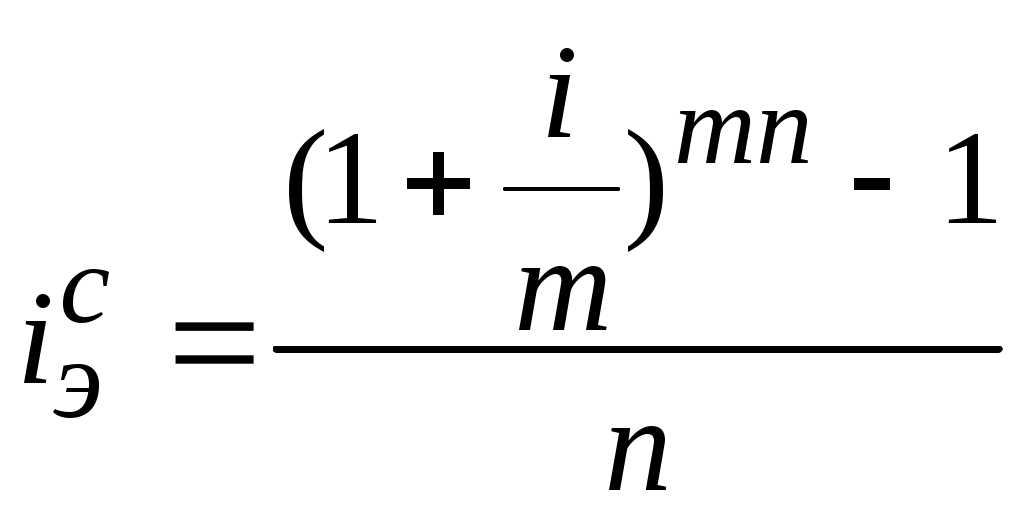(1.26) (1.27)
Задача 1.6. Финансовая компания в своем рекламном объявлении указывает, что вложенная сумма увеличивается на 0,46% ежедневно с начислением процентов на проценты (сложные проценты). Определить эффективную годовую ставку процентов при заключении договора с компанией на 3 месяца.

Решение

(1.27) = 2,05 или 205%


1.5. Расчеты в условиях инфляции
Инфляция характеризуется обесцениванием национальной валюты и общим повышением уровня цен.

Уровень инфляции (в %) показывает, на сколько выросли цены за рассматриваемый период времени:

% (1.28)

где - сумма, на которую надо увеличить первоначальную сумму для сохранения её покупательной способности в будущем.

- индекс инфляции (показывает во сколько раз выросли цены);

(1.29) (1.30)

Индекс инфляции за период, состоящий из

---

-го количества более коротких периодов, характеризующихся своим уровнем инфляции, можно определить по формуле:

(1.31)

где - общее количество интервалов в наблюдаемом периоде. Если есть месячные уровни инфляции, то в году будет 12 наблюдаемых периодов.

При равных интервалах и равных уровнях инфляции за каждый интервал формула принимает вид:

(1.32)

Будущую сумму , характеризующую реальное, обесцененное в результате инфляции значение настоящей суммы , можно определить по формуле:

(1.33)

Чтобы в условиях инфляции реальная покупательная способность будущих и современных сумм не отличалась, необходимо компенсировать потери от инфляции путем корректировки процентной ставки:

1. 
   Точная корректировка осуществляется по формуле:
   

(1.34)

где - ставка брутто – ставка, учитывающая действие инфляции;

- ставка процентов, характеризующая доходность операции без учета действия инфляции;

2. Приближённая корректировка:

(1.35)

Вычисленное значение ставки брутто или следует подставлять в расчетные формулы вместо ставки процентов .
Задача 1.7. Определить ожидаемый годовой уровень инфляции при оптимистическом прогнозе ее величины за месяц на уровне 1,5%.

---