ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 161
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ТЕХНИЧЕСКОЕ ОПИСАНИЕ МЕХАНИЗМА
2. ПРОЕКТИРОВОЧНЫЙ РАСЧЕТ МЕХАНИЗМА
3. ПРОВЕРОЧНЫЙ РАСЧЁТ ПЕРЕДАЧИ НА КОНТАКТНУЮ ПРОЧНОСТЬ
4.ПРОВЕРОЧНЫЙ РАСЧЁТ ПЕРЕДАЧИ НА ИЗГИБНУЮ ПРОЧНОСТЬ
5. ЭСКИЗНАЯ КОМПОНОВКА РЕДУКТОРА
7. ПРОВЕРОЧНЫЙ РАСЧЕТ ПОДШИПНИКОВ
8. ПРОВЕРОЧНЫЙ РАСЧЁТ ШЛИЦЕВОГО СОЕДИНЕНИЯ
9. ПРОВЕРОЧНЫЙ РАСЧЕТ БОЛТОВОГО СОЕДИНЕНИЯ
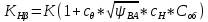 (2.8.1)
(2.8.1)где К - коэффициент неравномерности
К = 1 - для прямозубых пар
cH- коэффициент, учитывающий относительную твёрдость контактных поверхностей
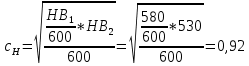 (2.8.2)
(2.8.2)Ψba=0,3 - по п.2.4
сθ- коэффициент, учитывающий влияние деформации скручивания шестерни и углов прогиба валов
сθ=0,2 - согласно заданной кинематической схеме рис. 1.3 [1]
Cоб - коэффициент, учитывающий влияние смягчения краев обода колеса
Соб=0,9 - принимая обод колеса податливым рис. 1.4[1]
После подстановки числовых значений в формулу (2.8.1):
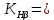 1*(1+0,2*
1*(1+0,2*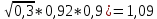 1
12.8.3 Коэффициент, учитывающий дополнительную нагрузку
В первом приближении: ΚΗV = 1
2.8.4 Функция ƒ(β)
ƒ(β) = 1- при прямых зубьях
2.9 Определение межосевого расстояния цилиндрической зубчатой передачи в первом приближении
 , мм (2.9.1)
, мм (2.9.1)где
T1 - номинальный вращательный момент на ведущем звене передачи (шестерне), Н*мм
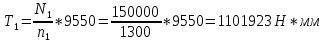 (2.9.2)
(2.9.2)Кд - коэффициент динамичности Кд = 1,05 (исходные данные)
Епр - приведённый модуль упругости материала шестерни и колеса, МПа
Для стали Eпр=E1=E2=2.1*105 МПа
KHα=1 - коэффициент, учитывающий распределение нагрузки между зубьями
После подстановки числовых значений в (2.9.1):
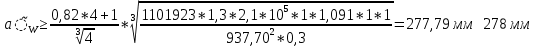
2.10 Определение модуля зацепления в первом приближении
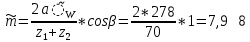 (2.10.1)
(2.10.1)Из табл. 1.7[1] выбираем стандартное значение модуля m = 8
2.11 Определение основных размеров зубчатой передачи
Диаметры делительных и начальных окружностей ( d и dw ) при коррегировании с коэффициентами смещения х1 + х2 = 0 совпадают, т.е.
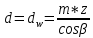 (2.11.1)
(2.11.1)Тогда для шестерни и колеса:
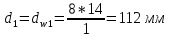
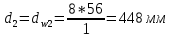
Диаметры окружностей вершины зубьев: da=d+2m+2xm (2.11.2)
da1=112+2*8+2*0,3*8=132,8 мм
da2=448+2*8-2*0,3*8=459,2 мм
Диаметры окружностей впадин зубьев: dƒ=d-2.5m+2xm(2.11.3)
dƒ1=112-2,5*8+2*0,3*8=96,8мм
dƒ2=448-2,5*8-2*0,3*8=423,2мм
Межосевое расстояние (окончательная величина):
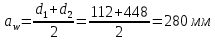
Примем за
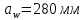 (2.11.4)
(2.11.4)Рабочая ширина венца в первом приближении:
b̃w=ψba*ãw=0,3*277,79=83,337мм (2.11.5)
Действительную ширину зубчатого венца получаем округлением в сторону увеличения до нормального линейного размера по табл. 1.12 [1]:
b1=105мм b2=85мм
Тогда окончательная величина рабочей ширины зубчатого венца (определяющая область действия контактных напряжений):
bw=min(b1,b2)=85мм
3. ПРОВЕРОЧНЫЙ РАСЧЁТ ПЕРЕДАЧИ НА КОНТАКТНУЮ ПРОЧНОСТЬ
Условие контактной прочности: σΗ<σΗΡ
σΗ - расчётные контактные напряжения
σΗΡ - допускаемое контактное напряжение (п.2.7)
Расчётные контактные напряжения для цилиндрической передачи:
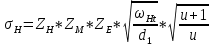 ,МПа (3.1)
,МПа (3.1)3.1Определение коэффициентов ΖΗ , ΖΜ , ΖΕ входящих в формулу для определения величины σΗ
3.1.1 Коэффициент учитывающий форму сопряжённых поверхностей зубьев
ΖΗ =1,76*cosβ = 1,76
3.1.2 Коэффициент учитывающий упругие свойства материалов зубьев
ZM= 270 МПа1/2 - для стальных зубьев
3.1.3 Коэффициент учитывающий суммарную длину контактных линий в зацеплении
ΖΕ = 1 - для прямых зубьев
3.2 Определение удельной расчётной окружной нагрузки на зубья при расчёте контактных напряжений
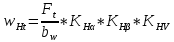 , H/мм (3.2.1)
, H/мм (3.2.1)где
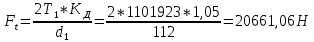 (3.2.2)
(3.2.2)bw=b2=85мм - по п. 2.11
KHα=1 - по п.2.8.1
KHβ=1,09 - по п.2.8.2
Коэффициент, учитывающий дополнительную динамическую нагрузку, принятый в первом приближении равным 1, теперь определяется по формуле:
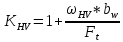 (3.2.3)
(3.2.3)где ωΗV - удельная окружная динамическая нагрузка на зубья, определяемая из неравенства
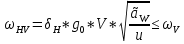 H/мм (3.2.4)
H/мм (3.2.4)Где
δΗ - коэффициент, учитывающий модификацию головки зуба и твердость рабочих поверхностей, выбирается из таблицы 1.9 [1]
δH=0,01 - для прямых зубьев с модификацией головок при НВ>350
g0- коэффициент, учитывающий погрешность зацепления по шагу, выбирается из таблицы 1.10 [1]
g0 = 53 - для степени точности при m =8 мм >3,55 мм
ωV - предельное значение удельной окружной динамической силы , выбирается из таблицы 1.10 [1]
ωV = 310 H / мм - для степени точности при m =8 мм >3,55 мм
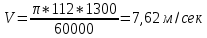
После подстановки числовых значений в формулу (3.2.4)
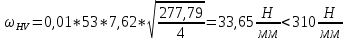
Так как неравенство выполняется, окончательное значение удельной окружной динамической нагрузки на зубья: ωΗV=
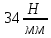
После подстановки числовых значений в формулы (3.2.3) и (3.2.1)
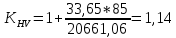
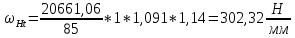
3.3 Определение расчётных контактных напряжений
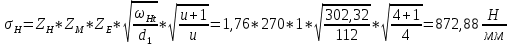
3.4 Проверка контактной прочности зубьев передачи
σH≤σHP
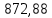 МПа<
МПа<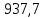 МПа
МПагде σΗΡ=
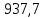 МПа - по п.2.7
МПа - по п.2.7Условие прочности выполняется
4.ПРОВЕРОЧНЫЙ РАСЧЁТ ПЕРЕДАЧИ НА ИЗГИБНУЮ ПРОЧНОСТЬ
Условие изгибной прочности для зубьев шестерни и колеса: σF1< σFΡ1 и
σF2< σFΡ2
σΡΧ 2 - расчётное местное изгибное напряжение на переходной поверхности у основания зуба
со стороны растяжения σF1, 2 - допускаемое изгибное напряжение
4.1 Определение расчётного местного напряжения у основания зуба шестерни и колеса σF1,2
Для цилиндрической передачи:
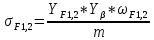 (4.1)
(4.1)4.1.1 Коэффициент, учитывающий форму профиля зуба для колёс с наружными зубьями
YF1,2=
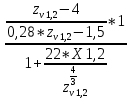 (4.1.1)
(4.1.1)| где | zv1=z1=16 | -для прямых зубьев |
| zv2=z2=48 |
x1=+0,3 x2=-0,3 x1 и x2-коэффициенты смещения инструмента
После подстановки числовых значений
YF1=
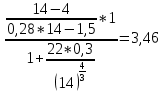
YF2=
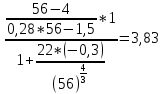
4.1.2 Коэффициент, учитывающий наклон линии зуба
Υβ= 1 - для прямых зубьев
4.1.3 Определение удельной расчётной окружной нагрузки на зубья при расчёте на изгиб
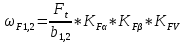 , (4.1.2)
, (4.1.2)где
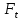 =
=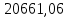 Н - по п.3.2
Н - по п.3.2b1,2 - действительная ширина зубчатого венца шестерни или колеса
b1=105мм, b2 = 85мм - по п.2.11
Коэффициент, учитывающий распределение нагрузки между зубьями при расчёте на изгиб
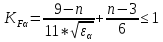 (4.1.3)
(4.1.3)где
n - степень точности зацепления n =8
εα- коэффициент торцевого перекрытия зубьев
εα1и εα2- частные коэффициенты перекрытия , выбираемые согласно рекомендациям п.2.8.4 с помощью графика рис.1.6
εα=εα1(1+x1)+ εα2(1+x2)= 0,77*(1+0.3)+0,86*(1-0,3)=1,6(4.1.4)
После подстановки числовых значений в формулу (4.1.3)